基于速度阻尼力位切换DSP 算法的引线键合机邦头设计
2014-11-18陈永刚阎秋生巩航军
陈永刚,阎秋生,巩航军
(1.东莞职业技术学院,广东东莞 523808;2.广东工业大学,广东广州 510006)
LED 焊线机设备中,键合邦头的运动过程是LED 芯片焊接的关键。其工作原理是将引线框架固定在加热块上,再施加超声波、键合力,在芯片或引脚与金属线的结合部位形成金属焊[1]。从控制理论角度出发,可以将整个芯片焊接运动过程分为以下几个部分:位置控制、力控制、力位切换控制[2]。位置控制实现引线键合邦头在自由运动状态下的高速高精度控制,包括高速运动和低速搜索以及金丝线的拉弧运动;力控制是控制芯片焊接时焊接加力的稳定。而力切换控制是实现键合邦头从位置控制到力控制的连接纽带,对抑制切换过程中冲击力的产生有重要作用,目前常采用的直接力位切换算法因为没有抑制力位切换过程中的速度波动,造成了力波动过大。因此根据国内外研究现状,以国内研发的最新型全自动LED焊线机为背景,提出一套基于DSP 的速度阻尼力位切换控制系统。
1 力位切换控制分析
如图1 所示,在芯片焊接过程中,当键合邦头在位置控制下完成自由状态下运动,键合邦头末端劈刀接触芯片基板准备加力时的控制过程,称之为切换控制。力位切换控制过程是文中研究的重点,目的是实现迅速稳定的力位切换。
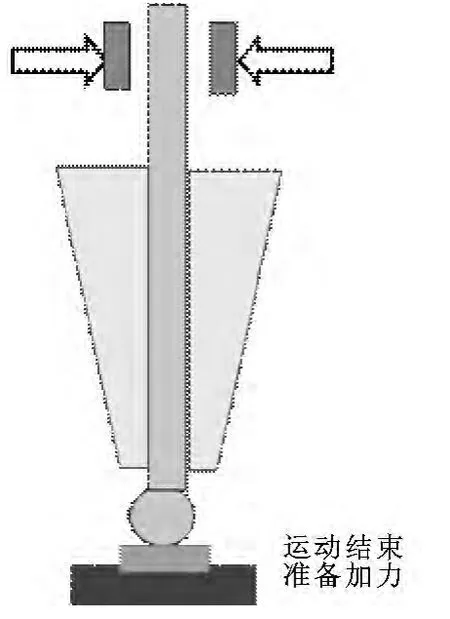
图1 力位切换控制
力位切换控制是众所周知的一大控制难题,国外最早的研究是关于机器操作手臂在抓取物体时的混合控制[3]。现在,力位切换控制仍然是机器人及自动化控制的前沿研究领域。对于力位切换控制,研究学者提出了很多新的控制思想与方法,比如动态混合力位控制、阻抗控制、非线性阻尼控制、自适应控制等[4-6]。文中从应用角度出发,分析切换过程与影响力位切换的相关因素,并对实现力位切换控制的策略作符合实际应用的理论分析与设计。
2 基于速度阻尼力位切换方案设计
基于速度阻尼的力位切换控制方法设计思想是:在键合邦头低速搜索阶段,检测位置偏差作为切换条件;在切换条件达到阈值时,将控制器切换到速度环加电流环控制环路方式。即通过速度环的调节实现力位切换前键合邦头运动速度的快速抑制,从而达到平稳切换的目的。设计框图如图2 所示。
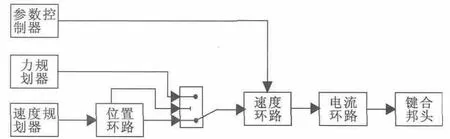
图2 带速度阻尼的力位切换框图
在图2 中,看上去有3 个前向通道,实际上只有两个通道:一个是以位置环为首组成的位置控制通道;另一个是以力规划器为首组成的力控制通道。参数控制器只是用来在进行力位切换时改变速度环参数用的参数规划表,并不是真正的自成环路。显而易见,与直接力位切换控制系统相比,环路切换开关提前了。切换条件的选择仍然是位置环路的位置偏差。
利用速度闭环构成的速度阻尼对切换速度精确的控制作用,使得键合邦头在力位切换过程中,缓冲键合邦头金属球与基板之间的碰撞力[7],使得金属球能够快速稳定,从而使得加力过程更平稳、力波动更小。虽然与直接力位切换控制系统相比,多保留了一个速度环,但实际控制起来并不是想象中的那么简单。对于运动控制卡驱动器控制系统,从先前的双环控制,然后到模拟量力位切换,到保留一环并改变环路的参数,这样的一个“热”转变,还是很难做到的。
3 基于速度阻尼力位切换DSP 算法设计
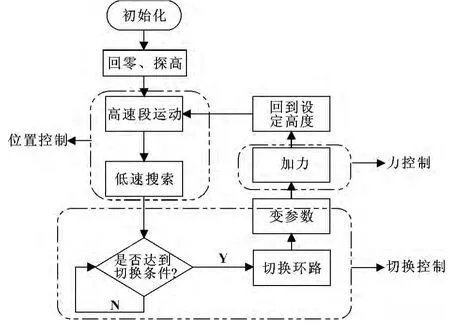
图3 带速度阻尼的力位切换算法流程图
基于速度阻尼力位切换DSP 算法设计,类似于直接力位切换DSP 算法设计,所不同的是在力位切换时,通过切换条件,保留了速度环,并通过设定速度环的参数,进而构成速度阻尼的作用。系统算法流程如图3 所示。
4 参数调试
为了使系统控制性能达到最优,必须对其环路控制参数进行调节。基于速度阻尼的力位切换控制系统,有3 个方面的控制参数需要调节:位置环路的控制参数、速度阻尼参数、力控制环路参数。
(1)位置环路的控制参数的调试,目标是使系统具有良好的跟踪定位精度,实现高速高精度的运动控制性能。包含位置环路的PID 参数、速度前馈与加速度前馈系数、速度环路的PID 参数共8 个参数的调节。一般选择从内环往外环调试,即先调节速度环路,达到设计要求后,再调节位置环路。速度环路调节完毕后,调节位置环路的Kp、速度前馈、加速度前馈3 个系数。调节好这3 个参数后,然后通过调节Ki使得系统无稳态误差,调节Kd抑制系统的超调;
(2)速度阻尼参数的调试,目标是尽量降低力位切换过程中的速度波动,使得加力过程更加平稳。通过改变速度环路控制律的参数,主要是Kp,使得速度环路构成一个阻尼器,以使系统更加稳定;
(3)力控制环路参数的调试,目标是使加力过程更加平稳,力波动尽可能地小。力控制律设计为PD控制器。调节过程分为两个步骤:首先将Kp尽可能地放大,以快速抑制系统的振动;然后将Kp减小,同时加大Kd,使得系统的超调大大减少。
5 结束语
采用三角波速度信号作为力位切换的激励信号。设定的焊接力有两段:第一段力为0.75 N,第二段力为1.05 N,加力时间均为5 ms,实际力响应曲线如图4 所示。
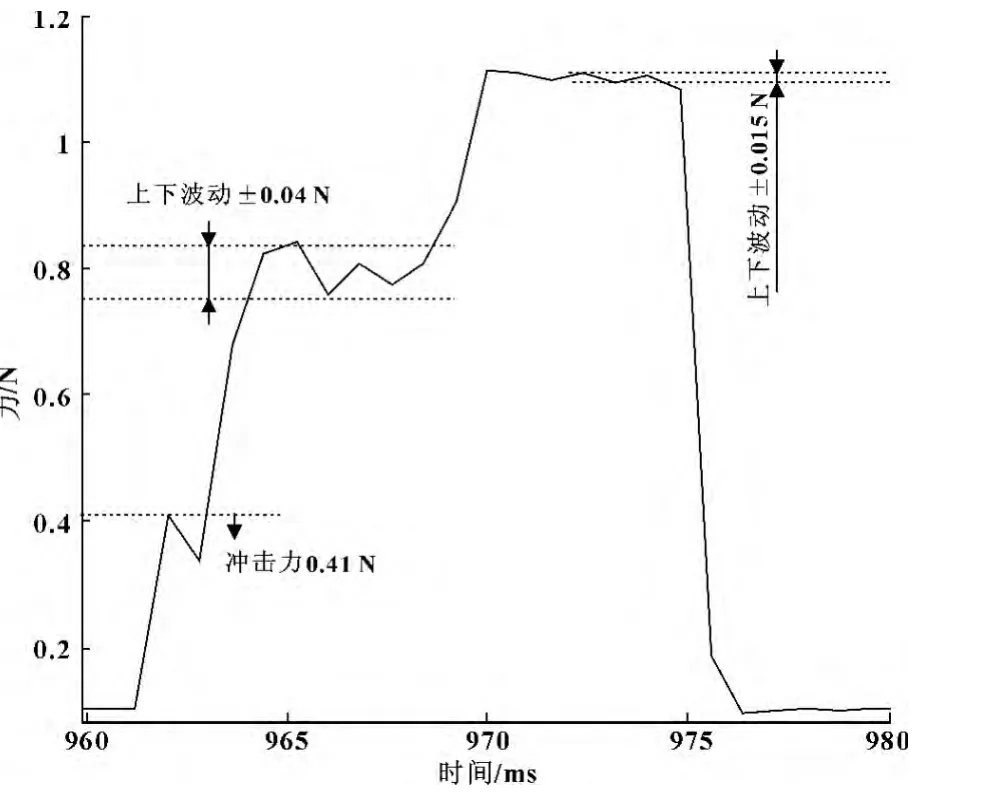
图4 带速度阻尼的力位切换算法力响应曲线
从图5 可以看出:相比于直接力位切换控制,基于速度阻尼的力位切换控制效果要好得多,力波动明显减小,冲击力最大为0.41 N,反弹力为0,加力段力波动效果接近±0.03 N 设计要求范围。这说明:在整个力位切换过程中,加力平稳,键合邦头在力位切换过程中的振动得到了很好的抑制,也即速度阻尼的作用效果明显。
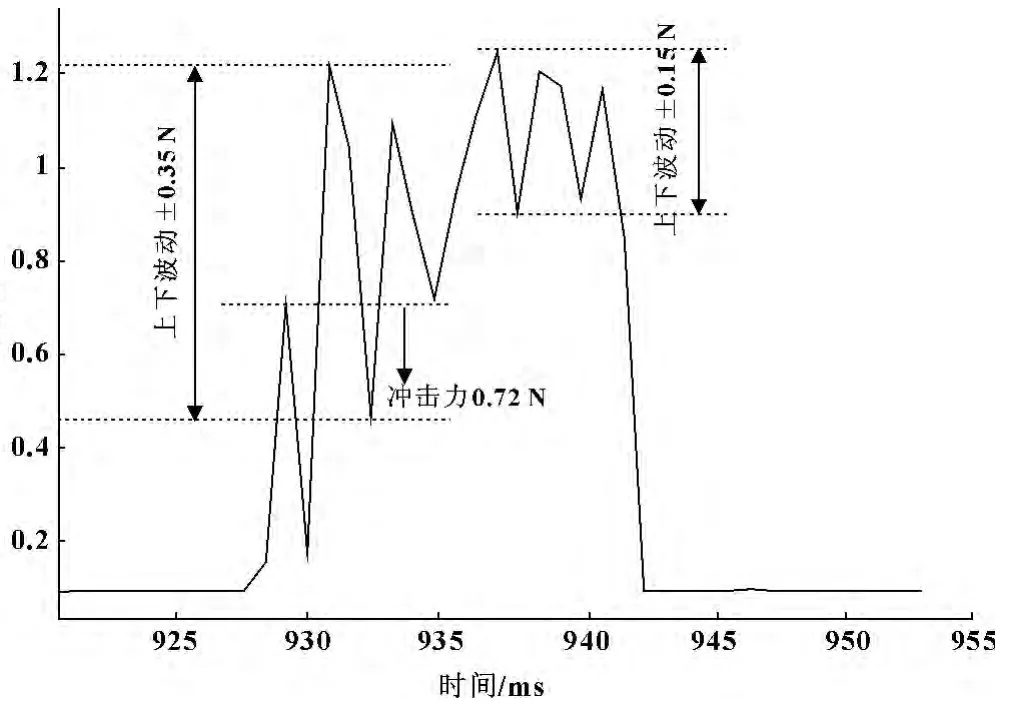
图5 直接力位切换算法的力响应曲线
[1]李元升.引线键合机工艺技术分析[J].电子工业专用设备,2004(3):78-81.
[2]XU W L,HAN J D,TSO S K.Experimental Study of Contact Transition Control Incorporating Joint Acceleration Feedback[J].Mechatronics,2000,5(3):292-301.
[3]HSIEN I L,CHEN C L.A Hybrid Control Policy of Robot Arm Motion for Assistive Robots[C]// Information and Automation,2011:163-168.
[4]HYDE J M,CUTKOSKY M R.Contact Transition Control:An Experimental Study[C]//Robotics and Automation,1993:363-368.
[5]BHASIN S,DUPREE K,WILCOX Z D,et al.Adaptive Control of a Robotic System Undergoing a Non-Contact to Contact Transition with a Viscoelastic Environment[C]//American Control Conference,2009:3506-3511.
[6]TO Y K.Analysis and Implementation of Force Control in Industrial Application[D].HongKong:HongKong University of Science and Technology,2001:29-37.
[7]KRIPESH V,SIVAKUMAR M,LIM L A,et al.Wire Bonding Process Impact on Low-K Dielectric Material in Damascene Copper Integrated Circuits[C]//Electronic Components and Technology Conference,2002:876-880.
