锚固框架结构加固公路边坡的优化设计
2014-11-17臧俊玲
臧俊玲
(保定市交通局公路工程质量监督站,河北 保定 071000)
0 引言
近年来随着我国交通、城市建设的高速发展,尤其是管理部门对公路工程的修建以及对边坡治理工程生态环境的重视,锚固框架结构在我国各类人工和自然边坡的整治工程中得到了日益广泛的应用,并逐步成为了一种主要的新型边坡加固与防护技术。
由锚杆、面层框架组成的锚固框架结构对边坡进行加固,既能降低被加固岩土土体的内部剪应力强度,又能提高力学强度,通过锚固框架结构与岩土土体结合,改善原本不稳定区坡体的受力状态。本文以河北某二级公路高陡边坡为实例,由于该公路属于政府二级还贷公路,经费有限,边坡维护不可能采取高速公路那样昂贵的防护措施,所以有必要对边坡加固的工程成本进行控制,即对工程造价进行优化。本文依据优化设计的基本原理提出了锚固框架结构优化设计的方法与计算过程。
1 结构优化模型
根据优化设计原理,锚固框架结构优化设计可表述为:在满足相关约束条件下,寻求一组设计变量和成本函数,通过建立和求解数学模型,使治理工程的总造价为最小。参照相关规范,可建立如下锚固框架结构优化模型:

式中:梁截面高度为x1(mm);梁截面宽度为x2(mm);梁下部纵向钢筋截面面积为x3(mm);梁上部钢筋截面面积为x4(mm);混凝土成本为Cc(元);纵向钢筋成本为Cl(元);箍筋成本为Cg(元)。
为使成本最小,目标函数如下:
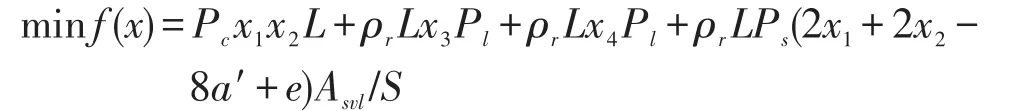
式中:Pc为混凝土单价(元/mm3);Pl、Ps分别是纵向钢筋与箍筋单价(元/kg);L为梁长(mm);ρr为钢筋密度(kg/mm3);a′为混凝土保护层厚度(mm);e为钢筋弯钩长度(mm);Asvl为单根箍筋截面面积(mm2);S为箍筋间距(mm)。
依据相关规范,分别建立如下约束方程。
1.1 正截面强度约束
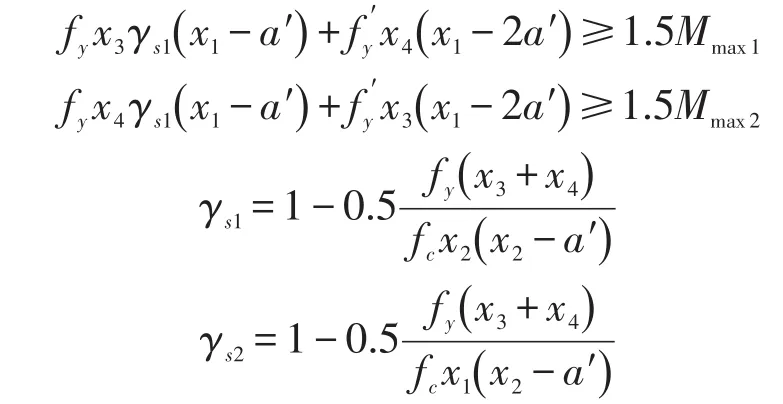
式中:Mmax1、Mmax2分别为格构梁在锚杆作用方向上的下部、上部最大弯矩设计值(N·mm2); fy、为钢筋抗拉、抗压强度(N/mm2); fc为混凝土轴心抗压强度设计值(N/mm2);γ为受压区混凝土塑性影响系数;
1.2 斜截面强度约束
对于此框架构件,其斜截面的受剪承载力应符合下列规定:
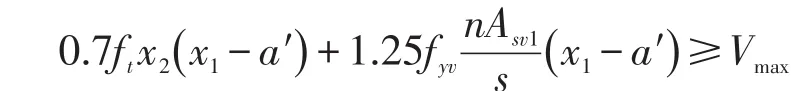
式中:Vmax为最大剪力设计值(N); ft为混凝土轴心抗拉强度设计值(N/mm2); fyv为箍筋抗拉强度设计值(N/mm2);n为箍筋支数。
1.3 纵向配筋约束
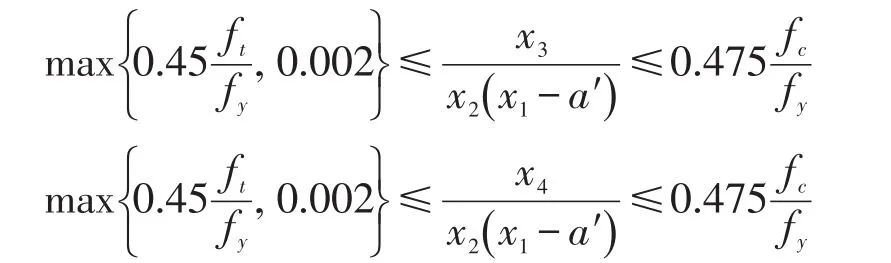
1.4 箍筋约束
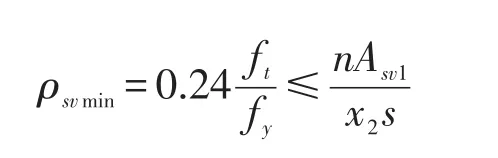
式中:ρsvmin为箍筋最小配筋率。
1.5 裂缝约束
框架梁构件中按荷载效应的标准组合并考虑长期作用影响的最大裂缝宽度(mm)可按下列公式计算:
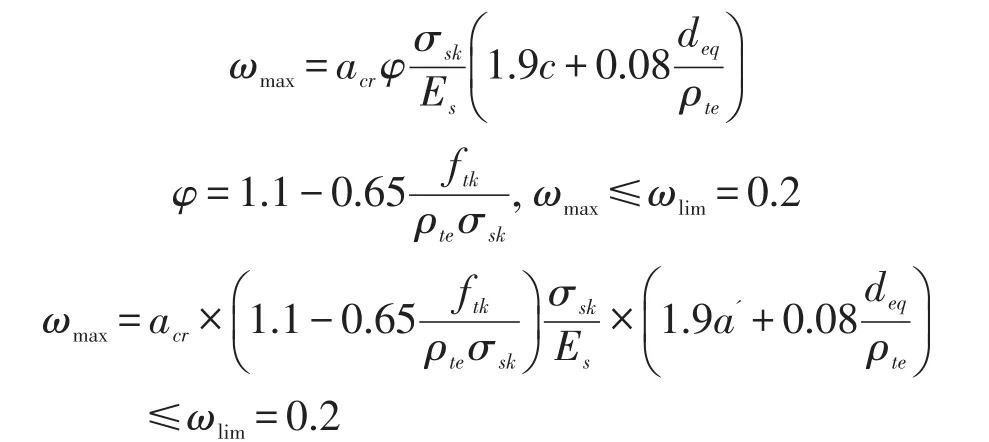
式中:acr为构件受力特征系数;φ为裂缝间纵向受拉钢筋应变不均匀系数;Es为钢筋弹性模量;ρte为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率;Ate为有效受拉混凝土截面面积;deq为受拉区纵向钢筋的有效直径(mm); ftk为混凝土轴心抗拉强度标准值(N/mm2)。
1.6 断面约束
断面约束条件为:300≤x1≤500;250≤x2≤400;300≤x3;300≤x4;x4≤x3;x2≤x1。
2 工程应用
2.1 工程概况
所选治理边坡为道路开挖所致,该段挖方路堑边坡主要为岩土混合边坡,边坡高度为725.2m,边坡下部,路基面以上4.5m范围内为强风化破碎岩石。原设计坡率为1∶0.75,按设计坡率切坡后,边坡上部出现较大范围的坍塌,坡顶距离坍塌口边缘10m远处出现裂缝。
由稳定性分析可知,该边坡总体上处于基本稳定状态,即当遇降雨、振动等不利外部因素作用时,有可能发生牵引式滑动失稳破坏。经方案论证,采用锚固框架结构治理方案。为达到节省工程造价目的,本文采用上述优化设计模型对治理工程方案进行结构优化设计。
2.2 计算和查询相关参数
根据工程类比,初选构纵梁断面为400mm×300mm,C25混凝土,对梁的内力进行计算,梁上、下部最大负弯矩为:=26.1kN·m,=40.5kN·m最大剪力为:Vmax=78kN。
依照《混凝土结构设计规范》(GB 50010—2002)等,力学参数及相关指标取值为:C25混凝土, Pc=255×10-9(元/mm3),HRB335钢筋, Pl=4.28(元/kg),HPB235钢筋,Ps=4.28(元/kg),a′=35mm,e=100mm,Asv1=50.3mm2,S=150mm, L=15×103mm。
2.3 模型计算
2.3.1 目标函数
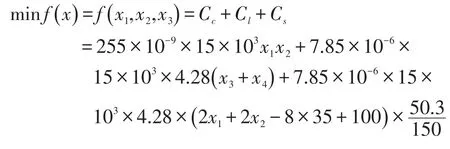
2.3.2 约束条件
(1)正截面约束

(6)断面约束
断面约束条件为:300≤x1≤500;250≤x2≤400;300≤x3;300≤x4;x4≤x3;x2≤x1。
2.3.3 优化结果
运用lingo11.0编程,对上述目标函数进行计算,可得到结果为:x1·x2=397×250;x3=373;x4=300;f(1)=906.8元。
为考察纵梁在上述约束条件下,三种常规断面尺寸对目标函数的影响,同时又拟定了寻优计算:x1·x2=400×300;x1·x2=350×300 。计算结果见表1。
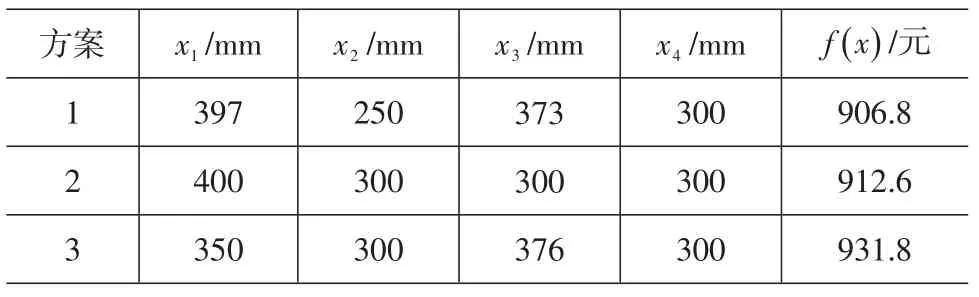
表1 优化结果
由表1可知, f(1)造价最低,框架梁的高宽比与其他方案比更合理,底部纵向受力钢筋截面面积大于。综合考虑,作为本治理工程纵梁最优结构设计断面。
同理,横梁按照上述针对纵梁的优化方法进行计算,优化计算结果为:x1·x2=300×250;x3=300;x4=300;f(1)=730.4元。
3 结语
本文依据有关现行规范与优化设计原理,建立了锚固框架的优化设计数学模型,给出了求解的方法和步骤,并编写了lingo11求解程序。通过在河北某二级公路边坡治理工程中的实际应用,得到优化设计后的结果,从而为支护结构提供了一种既经济又合理的结构设计计算方法。
[1]GB 50010—2002,混凝土结构设计规范[S].
[2]刘永明,傅旭东,邹勇.格构锚固技术及在高切坡防治中的应用[J].勘察科学技术,2006(3):24-27.
[3]范胜华,方坤,徐芳.格构梁预应力锚索在滑坡地质灾害中的应用[J].部探矿工程,2005,18(6);222-225.
[4]张炳华,候昶.土建结构优化设计[M].上海:同济大学出版社,1998.
