支持向量机在乌鲁木齐污染物预报中的应用研究

蔡 仁，李如琦，唐 冶，路光辉

（1.乌鲁木齐市气象局，新疆 乌鲁木齐830002；2.新疆气象台，新疆 乌鲁木齐830002）

世界卫生组织和联合国环境组织发表的一份报告说：“空气污染已成为全世界城市居民生活中一个无法逃避的现实”[1]。城市大气污染严重影响了社会正常生产和生活，大气污染已被发现与一系列的不健康结果有广泛关联[2]。控制大气污染、提高空气质量已成为世界各国环境综合治理的一个目标。作为城市大气污染治理的重要工作之一，城市空气污染预测有利于建立城市污染预报体系，可有效降低大气污染治理成本[3-4]。

乌鲁木齐是新疆维吾尔自治区首府，拥有人口330多万，是新疆经济、文化、政治中心，也是新疆最大的城市。乌鲁木齐位于天山北麓，准噶尔盆地南端，城市面积大约为339 km2，年平均降水量约208 mm，年平均气温为5.7℃，夏季最高温度为36℃，冬季最低温度为-25℃。年平均相对湿度为57%；最高月平均相对湿度出现在1月，为77%；最低月平均相对湿度出现在7月，为41%。乌鲁木齐重度空气污染基本出现在冬季的11月、12月、1月和2月[5-7]。随着乌鲁木齐市社会经济的快速发展、城市人口的迅速膨胀，大气污染问题日趋严重。2011年，世界卫生组织公布全球1 083个城市的空气质量排名（以年平均PM10浓度由小到大，包括中国32个城市），显示中国排名最后的3个城市是：乌鲁木齐（1 053名）、西宁（1 054名）和兰州（1 059名）[8]。为了更好地反映环境污染变化趋势，加强空气污染防治，预防严重的污染事件发生，研究大气污染预测方法、开展大气污染预报意义重大。另外社会各方面对空气污染的关注越来越高，尤其对现代城市居民，空气污染预报越来越重要。空气污染物自动监测已经在城市普及开来，更早地向民众发布较为准确的大气污染预报就更加必要。根据环保部的分级方法[9]，当空气质量达到重度及以上污染且持续6 h将发布更高一级的预警信号。因此，预测未来6 h的大气污染物浓度对于空气污染预报具有重要的意义。

大气污染指数预测有数值模式方法和统计方法等。从国内外较成熟的数值模式来看，一般都需要较详细的源强度时空分布资料和分辨率很高的气象模式，而对于中国大多数城市来说，发展此类模式还处在起步阶段,技术尚不成熟。国内外对大气污染统计预报应用较为广泛，数值预报方法和传统统计预报方法有各自缺点[10]。目前监测技术的发展积累了大量的环境信息资料，如果能找到行之有效的方法或技术来揭示这些历史时序数据所隐藏的对人类有用的指数和信息，对于分析环境状况的变化、污染物的变迁和环境管理的变革将起到重要的作用。研究发现大气污染物浓度的变化具有较强的非线性特征，要对其进行较为准确的预测，就必须采用能捕捉非线性变化规律的预报方法。具有高度非线性映射能力的计算机模型——支持向量机和Elman神经网络为此提供了较有力的工具。支持向量机是基于统计学理论的新一代机器学习技术[11]，能较好地解决小样本、非线性、高维数和局部极小点等时机问题，已成为人工智能研究领域的研究热点之一。其遵循结构风险最小化原则，预测性能和推广能力非常好，因而成为应用领域研究的热点。Elman神经网络为动态回归网络，最主要的特点是具有“记忆”功能，且能够更好地反映系统的动态特性。2011年朱国栋[12]利用支持向量机方法预测乌鲁木齐机场多个气象要素，结果表明建立的预测模型有较好的稳定性，并且对上述预报对象均有较好的预测效果。2007年Stanislaw等[13]运用支持向量机建立了每日空气污染指数预报的模型。2008年，Salazar-Ruiz等[14]运用支持向量机和Elman网络建立对流层臭氧的预报模型，达到了预期的预报效果。2012年Yeganeh.B等[15]建立了基于支持向量机德黑兰市区一氧化碳（CO）浓度的逐小时和逐日预报分季节预测模型，结果表明支持向量机为大气污染物预测提供了一个重要选择。2003年Wang Wenjian等[16]利用人工神经网络方法预测臭氧（O3）的日最大值，结果臭氧最大值的逐日预测效果理想。Lu Weizhan等[17-18]在2005年和2008年利用支持向量机预测地表层臭氧和预估周围大气污染的趋势，预测结果表明支持向量机效果显著。Boznar等[19]在1993年以人工神经网络模型建立复杂地形下二氧化硫（SO2）短时预报方法，表明人工神经网络方法对短时预报有着理想效果。动态非线性Elman网络也被广泛应用于预测当中[20-23]。

本文基于乌鲁木齐的污染物浓度和气象要素观测数据，使用支持向量机和Elman神经网络方法建立未来6 h大气污染物浓度预报模型，尝试细化污染物浓度的预报方法，为提高当地大气污染物预报能力提供参考。

1 资料和方法

1.1 资料

本文使用的资料为2012年11月1日—2013年1月31日的逐6 h空气污染物（包括SO2、NO2和PM10）浓度和对应时刻的气象要素资料。污染物浓度资料由中国气象局乌鲁木齐沙漠气象研究所大气成分监测站提供；气象资料来自乌鲁木齐国家基准自动气象站，包含温度、湿度、能见度、气压和风速等五种气象观测资料。

1.2 方法介绍

1.2.1 支持向量机（SVM）方法

线性化方法是人们解决复杂问题的一种常用办法，支持向量机是将非线性问题通过“升维”的方法变换为线性问题来进行计算。在高维特征空间中得到的是问题的线性解，但与之相应的却是原来样本空间问题的非线性解。

利用SVM进行回归与预测的基本思想[24-25]是通过非线性映射将数据映射到高维特征空间Ω中，并在该特征空间进行线性回归：

考虑l个独立分布的学习样本T={（x1，y1），…，（xl，yl）}∈（X，Y）l，其中xl∈X∈Rn，yl∈Y∈R，i=1，2，…，l，在高维特征空间Ω中构造回归超平面。

用于回归分析的SVM主要有ε-SVR和v-SVR。在ε-SVR中，需要实现确定ε-不敏感损失函数中的参数ε，然而在某些情况下选择合适的ε并非易事。相比之下，v-SVR能够自动计算。因此文中以v-SVR为例予以说明。v-SVR将回归分析问题转化为求解一下优化问题：

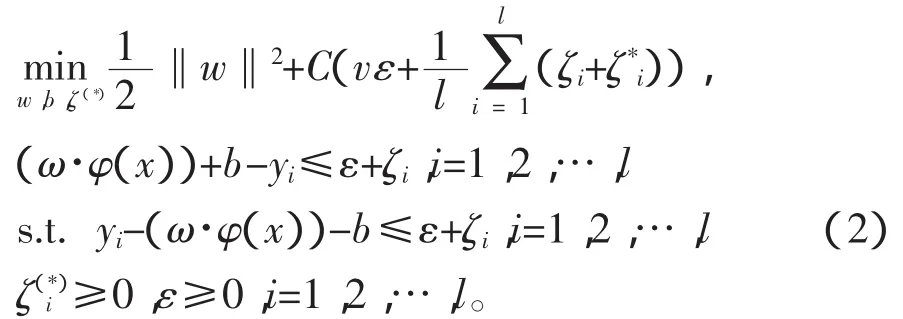
其中v≥0，C>0是常数。

所求的最优回归超平面的表达式为：

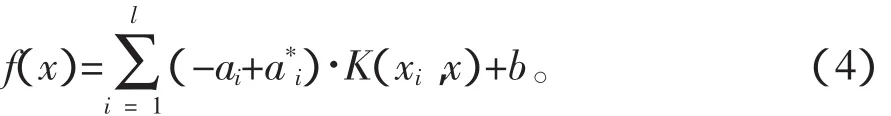
可以从式（4）看出，最优超平面的解析式完全由支持向量确定。最优超平面函数也是SVM方法最终确定的非线性回归函数。在实际求解过程中不需要知道非线性映射φ的显示表达式，这就大大简化了计算。依据Mercer定理定义的核函数K（xi，x）向量的维数无关，可以避免“维数灾难”。

1.2.2 Elman神经网络方法简介

Elman神经网络[26]是一种典型的动态回归神经网络，一般分为4层：输入层、中间层（隐含层）、承接层、输出层。其输入层、隐含层、输出层的连接类似于前馈网络，输入层的单元仅起信号传输作用，输出层单元起线性加权作用。隐含层单元的一步传递函数可采用线性或非线性函数，承接层又称为上下文层或状态层，它用来记忆隐含层单元前一时刻的输出值，可以认为是一个延时算子。

Elman神经网络的特点是隐含层的输出通过承接层的延迟与存储，自联到隐含层的输入，这种自联方式使其对历史状态的数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到了动态建模的目的。

Elman神经网络的非线性状态空间表达式为：

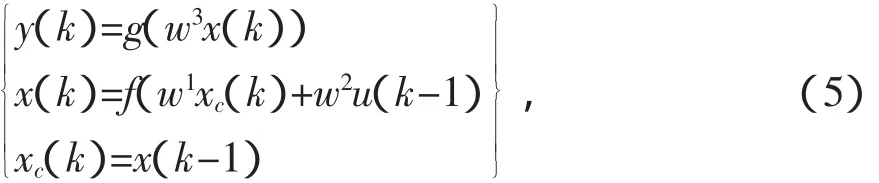
式（5）中：k为神经网络训练的次数；y为n维输出向量；x为隐层神经元输出向量；u为输入向量；xc为反馈状态向量；w3、w2、w1分别表示隐层到输出层、输入层到隐层、承接层到隐层的链接权重矩阵；g（*）为输出神经元的传递函数，是中间层输出的线性组合；f（*）为隐层神经元的传递函数，Elman神经网络采用BP算法进行权值修正，学习指标函数采用误差平方和函数：

其中yi（k）为期望输出值。

2 预报因子选取

黄忠[27]在乌鲁木齐市重污染天气与气象因素变化的影响分析中指出，气压、风、温度、雾等气象要素对PM10的影响相当显著。王式功等[28]研究指出兰州市区CO和氮氧化物及SO2之间存在显著相关。王英等[29]指出，北京市PM10与CO浓度存在季节性线性或非线性关系。姚从容等[29]研究表明天津市PM10和SO2时间变化具有高度相关性。

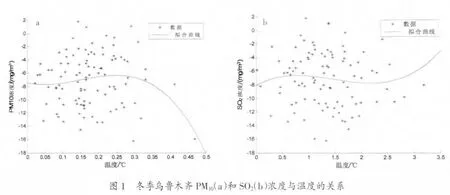
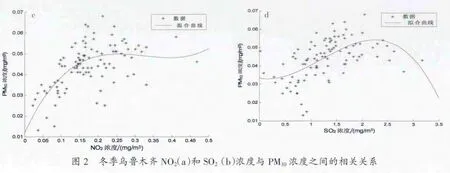
图1显示了冬季乌鲁木齐PM10和SO2浓度与温度的关系。由图可见，气温和PM10、SO2浓度存在一定的相关关系，其中PM10与温度的相关系数为0.574 4，SO2与温度的相关系数为-0.320 8，通过了显著性检验（t检验P<0.01）。其它污染物浓度分布与气象要素为非线性的复杂关系，这意味着，这些量的预测需要依赖复杂的非线性模型。图2表明了冬季SO2浓度与PM10浓度（图2a）间均存在负相关关系，相关系数为-0.327 8，而SO2浓度与和PM10浓度（图2b）之间的相关系数为0.335 4。

3 大气污染物非线性预报模型

3.1 数据选择与处理

2012年夏季，乌鲁木齐市实行了大规模的煤改气工程，冬季供暖模式发生本质变化，这样导致过去冬季的空气污染数据失去了参考价值，因此可以作为训练模型的数据量相对较少。图3为2011年12月和2012年12月乌鲁木齐是大气污染物PM10日变化图，可以看出，经过煤改气后乌鲁木齐大气污染物PM10浓度发生很大变化，故2012年7月以前的数据对于预报已无太大用处。因此，本文选用2012年11月1日至2013年1月31日的数据作为训练和预测。因为输入因子数据（SO2，NO2）、PM10、温度、湿度、能见度、风速、气压）不在一个数量级上，为了使网络收敛和训练时间变短，本文利用Matlab自带函数mapminmax将输入因子数据归一化到-1～1之间。

3.2 支持向量机（SVM）预报模型建立及预报结果评价

6 h污染物浓度预报模型是基于污染物浓度和气象要素而建立的，气象要素包括温度、湿度、风速、气压和能见度。模型输入训练数据为500个，输入的因子（图4a）为t时刻PM10（t）或SO2（t）或NO2（t）、PM10（t-1）、SO2（t-1）、NO2（t-1）、温 度（Temperature（t-1））、湿度（Humidity（t-1））、风速（Wind speed（t-1））、气压（Pressure（t-1））和能见度（Visibility（t-1）），输出分别为PM10（t）、SO2（t）、NO2（t）浓度t时刻预报模型。模型预测数据104个，输入因子（图4b）为PM10（t）、SO2（t）、NO2（t）、温度（Temperature（t））、湿度（Humidity（t））、风速（Wind speed（t））、气压（Pressure（t））和能见度（Visibility（t）），输出分别为t+1时刻（未来6 h）的污染物浓度预测值。

图4为SO2、NO2和PM10三种污染物基于支持向量机的预测结果和相对误差。

PM10和SO2的绝对误差略大，这与大气逆温层有直接关系[31]，魏疆等认为“逆温层厚度对PM10浓度的影响最大，其次是SO2，影响最小的为NO2”。由于大气探测每天只进行2次，分别为08时和20时，对于6 h预测有一定的局限性，本文未将大气逆温层作为因子输入，成为PM10预测误差略大的原因。SO2的预测误差较大的原因除了与逆温层厚度有关外，还与SO2在大气中的浓度会随时间的变化而变化，在小范围内有较大的随机性，不同的季节存在不同的分布等特性有关[32]，而NO2与以上大气逆温层的关系不密切，因此相对误差较小。

3.3 Elman神经网络预报模型建立及结果分析

Elman神经网络用同样的实验数据（3.2中用的数据），使用MATLAB自带的人工网络工具箱中的Elman网络建立预测模型，经过学习和训练，构造了一个含4层的Elman神经网络，该神经网络输入层有9个神经元，输出层有1个神经元，隐层神经元个数为19，此时模型的预测精度较高。通过建立的3个大气污染物的预测模型，分别预报逐6 h污染物浓度。结果表明基于Elman神经网络方法的三种污染物浓度预测值具有较好的趋势一致性，PM10和SO2的相对误差分别控制在35.4%和14.5%，平均绝对误差较大。由于没有引入逆温层厚度数据，Elman神经网络对PM10和SO2的预测效果都较差，这表明，Elman神经网络对相关性较好的数据较为敏感。

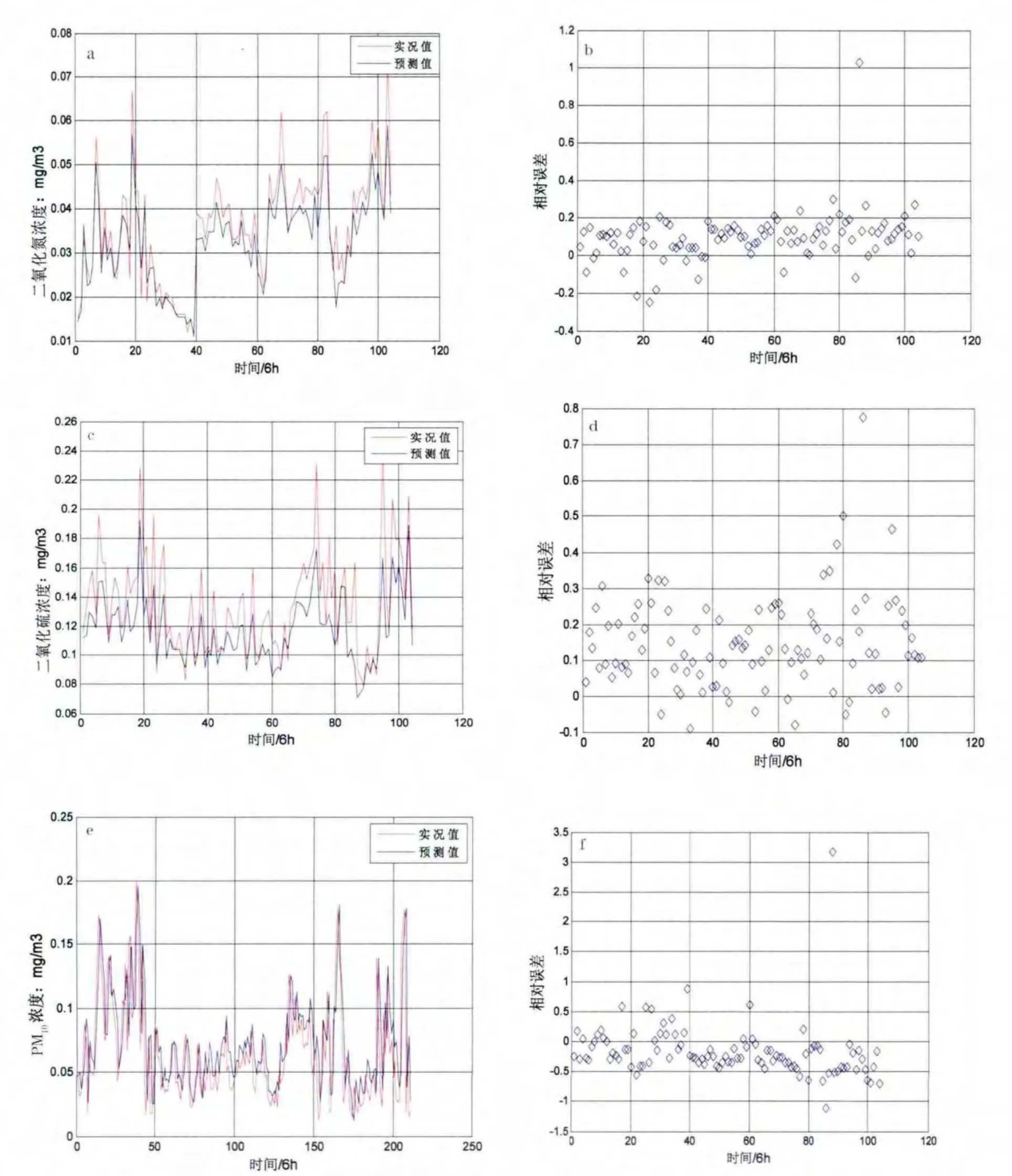
图4 基于支持向量机各种污染物浓度6 h的预测值及其相对误差

3.4 支持向量机（SVM）和Elman神经网络预测值的误差比较

表1给出了两种模型的3种污染物浓度预测误差的对比分析。两种模型对个别时间的预测效果不太理想，误差较大。表1表明支持向量机的预测值比Elman网络模型的预测值更加精确，原因可能有以下几点：（1）支持向量机是以统计学原理建立的[11]，它有严格的理论和数学基础，而Elman神经网络则依赖网络模型设计者的经验和对Elman网络的知识[26]；（2）Elman神经网络需要大量的实验数据去训练和学习，从而提高网络的预测能力，而支持向量机则可以用少量的实验数据得到较精确的预测结果；（3）支持向量机拥有非常好的泛化能力，能从最优超平面的划分得到最优的预测结果。（4）Elman网络对相关性较好的数据较为敏感，在输入数据上的考量较为严格。所以，支持向量机可以得到小样本试验的敏感性和特异性之间的最佳平衡，达到并给出较高精度的预测值。

表1 两种预测模型污染物浓度预测对比

4 结论

（1）污染物浓度与气象要素、不同污染物浓度之间都存在一定的相关关系：气温和SO2、NO2的浓度都有非常明显的线性相关性，而其它污染物浓度分布与各气象要素为非线性的复杂关系；SO2浓度与NO2浓度间存在负相关关系，而SO2浓度与和PM10浓度为正相关关系。

（2）本文尝试使用支持向量机和Elman网络模型预测乌鲁木齐市6 h短时空气污染物浓度。在预测的过程中，以污染物浓度（SO2，NO2，PM10）和气象要素（温度（Temperature）、湿度（Humidity）、风速（wind speed）、气压（pressure）和能见度（Visibility））作为输入因子，以SO2、NO2和PM103种污染物浓度分别作为输出因子通过两种预测模型进行训练输出。检验结果表明基于两种模型的3种污染物浓度预测值均具有较好的趋势一致性，3种污染物相比，PM10的绝对误差略大一些，相对误差SO2较大、NO2较小，两者预测值以偏大为主，PM10的相对误差则以偏小为主而无明显规律。从运用支持向量机和Elman神经网络两种模型预测SO2、NO2和PM10的浓度值的平均绝对误差、相对误差的对比分析来看，使用支持向量机预测大气污染物浓度较为精确，其相对误差为8.5%～16.6%，即支持向量机模型预测污染物浓度更好。以上分析表明，在乌鲁木齐市冬季采暖期燃料变化引起的大气污染物浓度数据不可用的情况下，通过两种模型预测结论的分析和比较表明，使用少量数据进行预测工作是可行的，而基于支持向量机模型的预测结果较为准确，参考价值更大，可靠性更高。

[1]美国健康效应研究所15号专题报告亚洲地区发展中国家大气污染对人体健康的影响[EB/OL].（2004-04-20）[2009-10-22].http://www.hongkongcan.org/doclib/200404-Health eggects of ootdoor air pollution developing countrise of Asia-Chinese.pdf，2004:9．

[2]Huang Wei，Tan Jianguo，Kan Haidong.Visibility，air quality and daily mortality in Shanghai,China[J].Science of the Total Environment，2009，407:3295-3300．

[3]刘振忠，董芃，王丽.城市大气环境污染预测与容量控制方法研究[J].电站系统工程，2005，14（4）：17-19．

[4]陈俏，曹根牛，陈柳.支持向量机应用于大气污染物浓度预测[J].计算机技术与发展，2010，20（1）：250-253．

[5]王春华，吕爱华，余晓丽.乌鲁木齐大气污染现状及影响因素分析[J].新疆农业大学学报，2010，33（4）：349-353．

[6]张新琪，海热提.吐尔逊.乌鲁木齐市大气环境容载力及污染防治对策研究[J].干旱区资源与环境，2001，15（3）：18-24．

[7]张杰，刘雪玲，任超霞.乌鲁木齐市大气污染成因分析及防止对策[J].新疆环境保护，2000，22（2）：65-70．

[8]The Urban Air Pollution Database,By Country and City（corrected version）.http://www.who.int/phe/health_topics/outdoorair/databases/en/index.html．

[9]GB 3095-1996，环境空气质量标准[S]．

[10]雷孝恩，张美根，韩志伟.大气污染数值预报基础[M].北京：气象出版社，1998．

[11]邓乃扬，田英杰.数据挖掘中的新方法-支持向量机[M].北京:科技出版社，2006：98-105．

[12]朱国栋.基于SVM方法的乌鲁木齐国际机场多要素预测[J].沙漠与绿洲气象，2011，5（4）：40-43．

[13]OsowskiS，Garanty K.Forecasting of the daily meteorological pollution using Wavelets and Support Vector Machine[J].Engineering Applications of Artificial Intelligence，2007，20：745-755．

[14]Salazer Ruiz E，Ordieres J B，Vergara E P.Development and comparative analysis of Tropospheric Ozone prediction models using linear and Artificial Intelligencebased models in Mexicali Baja California（Mexico）and Calexico，California （US）[J].Environmental modeling ＆ Software，2008，23：1056-1069．

[15]Yeganeh B，Shafie Pour Motlagh M.Prediction of CO concentrations based on a Hybrid Partial Least Square and Support Vector Machine model[J].Atmospheric Environment，2012，55:357-365．

[16]Wang Wenjian，Lu Weizhan，Wang Xiekang.Prediction of maximum daily ozone levelusing combined neural network and statistical characteristics[J].Environment International，2003，29：555-562．

[17]Lu Weizhan，Wang Dong.Ground-level Ozone prediction by Support Vector Machine approach with a costsenstitive classification Scheme[J].Science of the Total Environment，2008，395：109-116．

[18]Lu Weizhan，Wang，Wenjian.potential assessment of The“Support Vector Machine”method in forecasting ambient air pollutant trends[J].Chemosphere，2005，59：693-701．

[19]Boznar M，Lesjak M，Malkar.P.A Neural Networkbased method for short-term predictions of ambient SO2Concentrations in highly polluted industrial areas of complex terrain[J].Atmospheric Environment，1993，27：221-230．

[20]Marra S，Francesco M C．A new technique for solar activity forecasting using Recurrent Clman Networks[J]．International Journal of Information and Mathematical Sciences，2007，3（1）：8-13．

[21]Liu Jicheng，Niu Dongxiao.A novel Recurrent Neural Network forecasting model for power intelligence center[J]．J Cent South Univ Technol 2008，15:726-732．

[22]Shank D B，Hoogenboom G，Mcclendon R W.Dewpoint temperature prediction using artificial neural networks[J].Journal of Applied Meteorology and Climatology，2008，47:1757-1769．

[23]张超，常太华，刘欢，等．基于改进Elman神经网络的风速预测[J].华东电力，2012，40（8）：1412-1414．

[24]张学工.关于统计学习理论与支持向量机[J].自行化学报，2000，1:32-42．

[25]Vapnik V N.统计学习理论的本质[M].张学工译.北京：清华大学出版社，2000:96-98．

[26]飞思科技产品研发中心.神经网络理论与Matlab7实现[M].北京：电子工业出版社，2005，131-141．

[27]黄忠.乌鲁木齐市重污染天气与气象因素变化的影响分析[J].干旱环境监测，2005，19（3）：154-157．

[28]王式功，杨德保，黄建国.兰州城市八种主要空气污染物浓度分布类型及其相互关系[J].兰州大学学报：自然科学版，1996，32（1）：121-125．

[29]王英，金军，李令军.北京市基于PM10/CO关系的可吸入颗粒物自然源解析 [J].环境科学学报，2006，26（7）：1203-1208．

[30]姚从容，陈魁.城市环境空气质量变化规律及污染物特征分析[J].干旱区资源与环境，2007，21（5）：50-52．

[31]魏疆，王国华，任泉.乌鲁木齐市大气污染物浓度计量模型研究[J].干旱区地理，2011，28（5）：896-900．

[32]张美根，韩志伟，雷孝恩.城市空气污染预报方法简述[J].气候与环境研究，2001，6（1）：113-118．