基于混沌与量子粒子群算法相结合的负荷模型参数辨识研究

王振树 卞绍润 刘晓宇 于 凯 石云鹏

（1. 山东大学电气工程学院 济南 250061 2. 济南历城供电公司 济南 250100）

1 引言

电力系统数字仿真是现代电力系统进行科学研究、规划设计、调度运行和稳定控制的重要工具和手段[1-2]，仿真结果直接影响到相应电网决策方案的制定。而数字仿真计算结果的精度与所采用的模型和参数的准确性密切相关。现阶段，发电机和电网络模型已相当成熟，负荷模型则相对简单，已不能满足电力系统数字仿真结果精度和可信度的要求。在20世纪70年代末美国电力研究院（Electric Power Research Institute, EPRI）立项研究负荷建模未果后，电力系统一直采用能仿真出“保守”结果的负荷模型来解决负荷模型不准确的问题。随着电力系统稳定器（Power System Stabilizer，PSS）在发电机中的广泛应用，找不到一个对所有故障都“保守”的负荷模型，PSS与不准确的负荷模型相互作用有可能会使仿真结果从“保守”变为“乐观”[3]。1996年、2000年在北美发生了两次大停电事故，事后做事故仿真重现时，采用WSCC（Western System Coordinating Council）数据库中的负荷模型和参数不能得到与现场记录一致的仿真结果。通过对负荷模型修改，才得到与现场记录一致的仿真结果[4,5]。因此，建立能够反映负荷特性的准确负荷模型对电力系统仿真和安全稳定运行至关重要。

时至今日，人们已提出了不少负荷建模方法，这些方法可以归纳为统计综合法[6,7]、总体测辨法[8,9]和故障仿真法[10]。总体测辨法的基本思想是将综合负荷作为一整体，利用现场采集的测量数据辨识负荷模型结构和参数，具有简单、实用且基于实测数据等优点，是解决成千上万用电设备构成的负荷建模困难的一个可行办法。负荷特性数据、负荷模型结构以及参数辨识是影响实测负荷建模结果的重要因素。近年来，广域测量系统、故障录波监测系统及电能质量监测系统等在电力系统中的广泛应用为精确负荷特性数据的获取提供了有利条件[11-14]。电力故障录波监测系统有效记录故障时其安装处各电气量瞬时值变化的波形，能够准确捕获到电力系统故障前、故障时和故障后动态、暂态过程精确的数据信息[15]。本文利用电力故障录波装置记录的三相故障数据来进行实测负荷建模研究。

负荷模型的参数辨识方法大体可以分为线性和非线性两类。线性方法包括最小二乘估计、卡尔曼滤波[16]等方法，对于参数线性模型通常是有效的。非线性参数辨识方法目前大多以优化基础，其主要过程是寻找一组最优的参数向量，使得预定的误差目标函数达到最小，主要有梯度方法、随机搜索方法以及模拟进化方法。其中模拟进化方法适用范围广，找到全局最优解或近乎全局最优解的可能性大，属于随机优化方法，计算效率比传统随机搜索方法要高得多。文献[17]在对自适应的三层前馈网络（ABP）进行修改、简化后，得到简化（或线性）前馈网络（LBP），应用 LBP对负荷静态模型即幂函数和多项式模型的参数进行了辨识；文献[18]将遗传算法（GA）和 Levenberg-Marquardt算法有机结合并应用于综合负荷模型参数辨识，提高了辨识精度和计算效率；文献[19]中应用PSO算法进行电力系统负荷模型的参数辨识，与随机类方法中的 GA相比，PSO算法收敛速度更快，在同等时间内以更高的全局最优概率求解负荷参数。

PSO算法虽然简单易行，但其中粒子的位置更新是建立在速度更新的基础上，即收敛性是以经典力学中轨道的形式实现，速度更新的局限性限制了算法的全局搜索能力。Burgh证明了标准PSO算法不能收敛于全局最优解，甚至局部最优解[20]。QDPSO算法利用量子力学中的粒子具有不确定轨迹的行为特点来改变粒子位置，使粒子每次迭代时其运动轨迹的可能区域充满整个可行域，从而大大扩大了粒子的搜索范围，具有更好的全局收敛能力[21]。QDPSO算法已经成功应用于系统辨识[22]、QoS组播路由[23]和多目标设计优化[24]等领域。COA直接采用混沌变量进行寻优搜索，不需要优化的问题具有连续性和可微性，其搜索过程完全按照混沌运动自身的规律进行，因而利用混沌进行优化搜索更为简单、方便[25,26]。本文将COA与QDPSO相结合，并成功应用于负荷模型参数辨识。QDPSO用于全局搜索，而COA则根据QDPSO的结果进行局部搜索。

2 混沌与量子粒子群相结合的算法

2.1 混沌优化方法

混沌是非线性系统中的一种较为普遍的现象，具有随机性、遍历性和规律性的特点。在优化设计领域中，混沌现象的遍历性特点可以作为搜索过程中避免陷入局部极小的一种优化机制。COA的基本思想就是用类似载波的方法利用混沌映射将混沌状态引入到优化变量中，并把混沌运动的遍历范围放大到优化变量的取值范围，然后利用混沌变量进行搜索，并将此方法应用于连续复杂对象的优化问题。采用Logistic映射的混沌优化算法步骤如下：

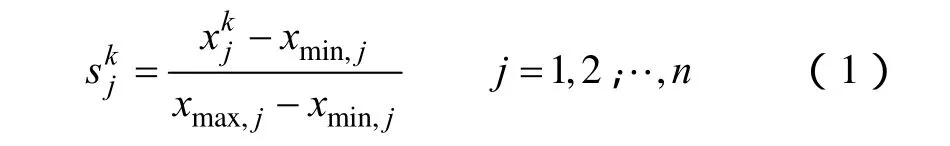
式中，xmax,j和 xmin,j分别为第j维变量的搜索上、下界。

（2）计算下次代迭代的混沌变量

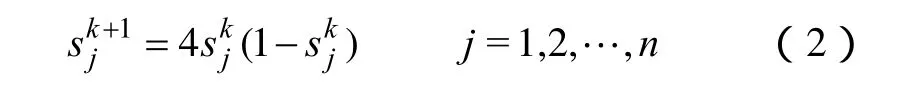
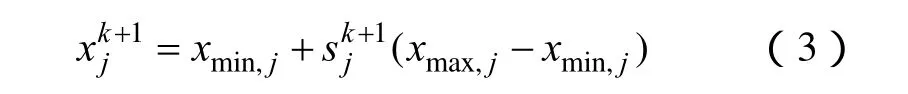
已达到最大迭代步数，将新解作为混沌优化的结果，否则置k=k+1，转到（2），继续迭代。

2.2 量子粒子群算法

2004年，Sun研究了吸收有关粒子收敛行为，并结合量子力学的模型，提出了量子粒子群算法。在量子力学中，每一个粒子在搜索空间移动时，都存在着一个以 p为中心的 DELTA势阱。在量子空间中的粒子满足聚集态的性质与经典力学中的完全不同；具有量子行为的粒子在移动时没有确定的轨迹，即速度和位置具有不确定性，并且这种不确定性使得粒子可能到达的位置“处处”（即整个可行解区域内）充满可能性，粒子具有了摆脱干扰性大的局部最优值点的可能性。它能保证算法的全局收敛并且在优化模型中只有位置向量，没有速度向量，控制参数少，寻优能力强。

QDPSO算法描述如下：在D维空间中，有m

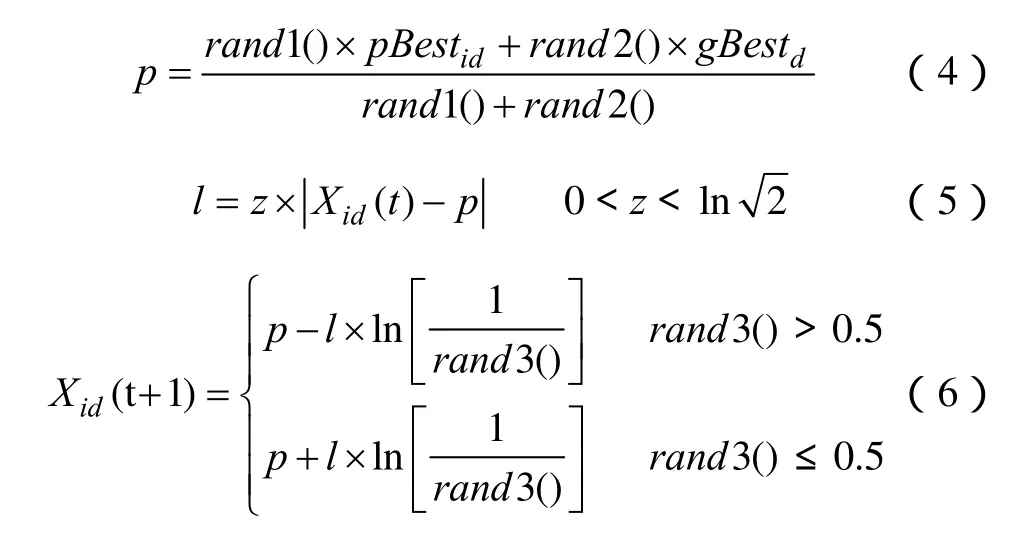
2.3 混沌与量子粒子群相结合算法

混沌与量子粒子群相结合算法的基本步骤如下：

（1）初始化。设置迭代次数，在D维空间，随机生成m个D维的随机数作为粒子初始位置X。

（2）由优化函数计算出每个粒子当前的适应值，并和各自的个体历史最优解对应的适应值进行比较，若当前的适应值优于个体历史最优解对应的适应值，则把当前解替换为个体最优解 pBesti，否则不替换。

（3）通过比较所有粒子最优的适应值来确定当前种群的最优解gBest。

（4）更新每个粒子的位置，计算每个粒子的适应值，然后保留群体中性能最好的粒子。

（5）对群体中的最佳粒子执行混沌优化算法，并更新其pBest和群体gBest。

（6）根据预先设定的精度要求和最大的迭代次数要求判断当前迭代是否达到要求，若未达到，则返回（2）继续迭代；若达到，则停止迭代，输出优化结果。

3 负荷模型及参数辨识

针对传统综合负荷模型没有计及配电网络的阻抗和无功补偿的缺点，文献[27]根据变电站负荷的实际构成，提出了考虑配电网络的综合负荷模型，较好地弥补了现有负荷模型的不足，具有物理结构合理、可操作性强等优点，能够方便地模拟负荷元件，包括配电网络、无功补偿系统。考虑配电网络的综合负荷模型结构如图1所示。

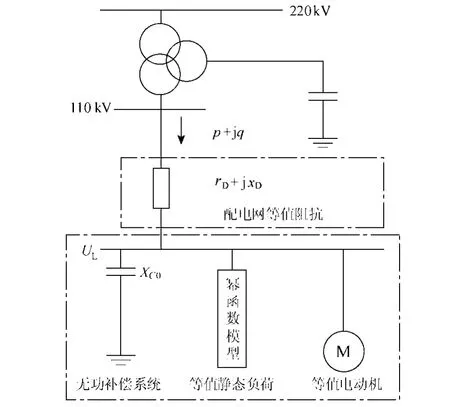
图1 考虑配电网络的综合负荷模型结构Fig.1 Structure of synthesis load model with distribution network忽略频率变化的影响，图1中的等值静态负荷部分可表示为

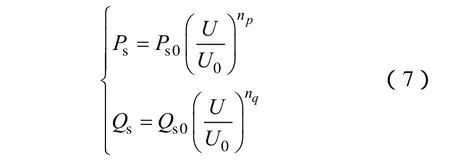
式中，np、nq分别为有功电压特征系数和无功电压特征系数。

等值电动机部分采用计及机电暂态的三阶模型，方程如下

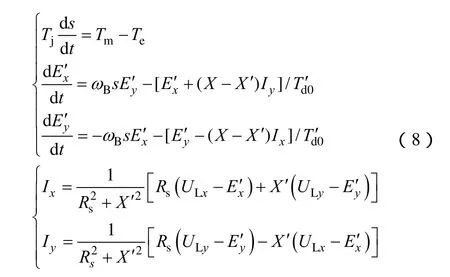
考虑电动机的比例PMP，该模型共有15个独立参数需要辨识

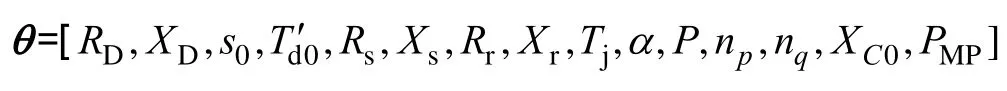
参数辨识的目标函数为

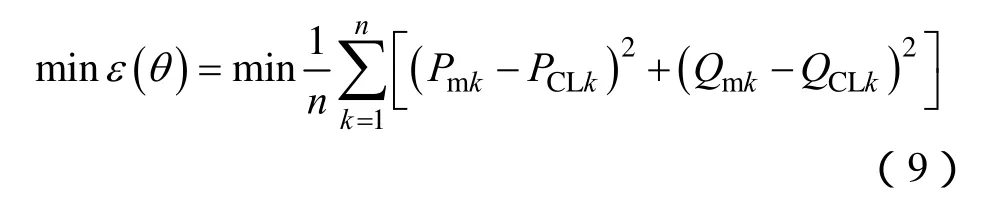
式中，Pmk、Qmk为实测有功功率和无功功率；PCLk、QCLk为模型输出的有功功率和无功功率；n为样本点的个数。

4 算例

本文将COA与QDPSO相结合的算法应用于解决负荷模型参数辨识这一典型的优化问题，在对实测扰动数据进行预处理的基础上，选取考虑配电网的综合负荷模型利用CQDPSO算法进行参数辨识，对CQDPSO算法用于综合负荷模型参数辨识的有效性进行验证。

2012年，山东电网某220kV线路因发生三相故障跳闸，安装在各变电站的故障录波装置记录下了各变电站扰动前后三相电压、电流的瞬时值。本文采用220kV东城站的故障录波数据进行负荷模型的参数辨识，如图2所示。对故障录波数据中数据进行预处理，取粒子数为 60，迭代次数为 50，采用CQDPSO算法对考虑配电网络的综合负荷模型进行参数辨识。由于参数的灵敏度较小，故可直接将其取为典型值

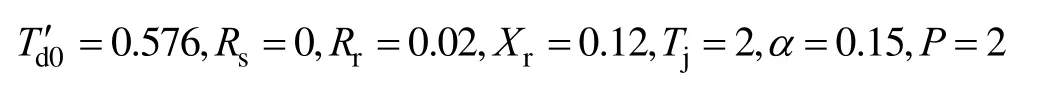
对剩余的8个参数进行辨识。有功功率的模型输出与实测响应对比如图3b所示，无功功率的模型输出与实测响应对比如图3c所示。

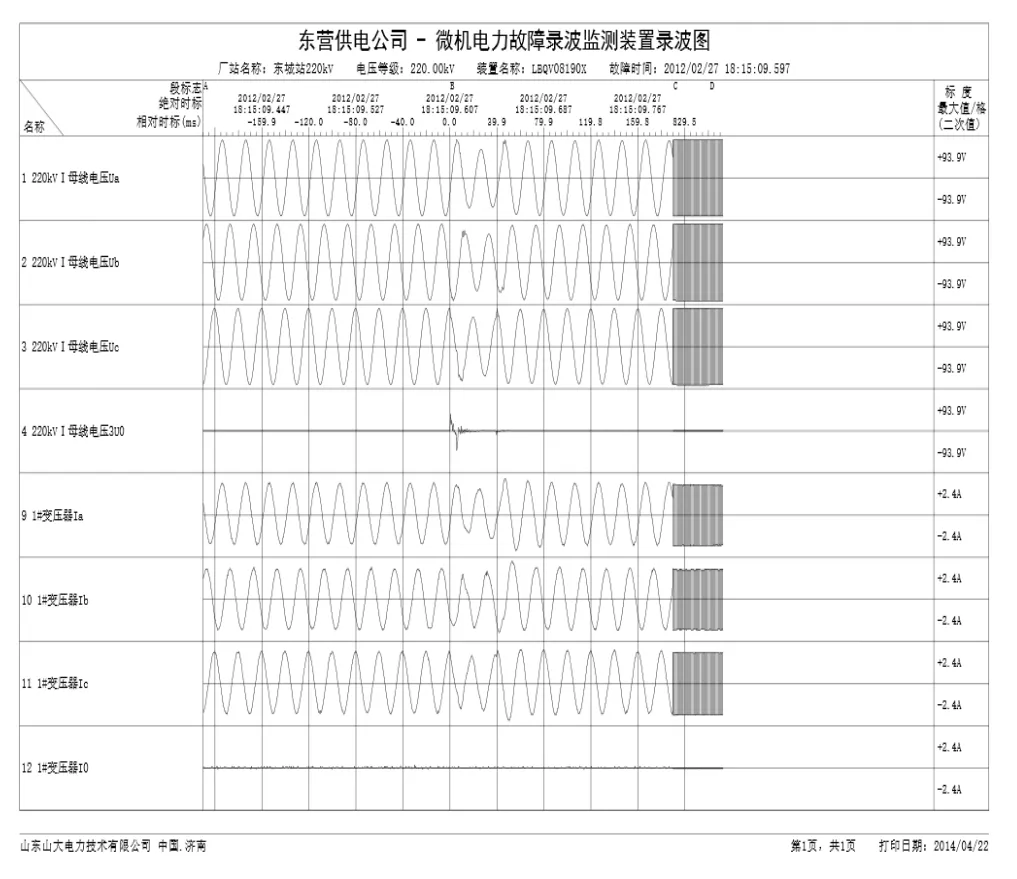
图2 东城站1#变压器电压电流故障录波Fig.2 The current and voltage signals of #1 transformer of Dongcheng

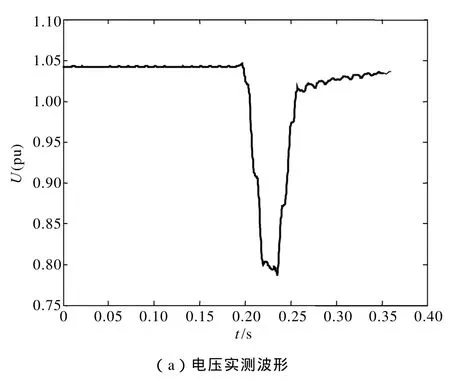
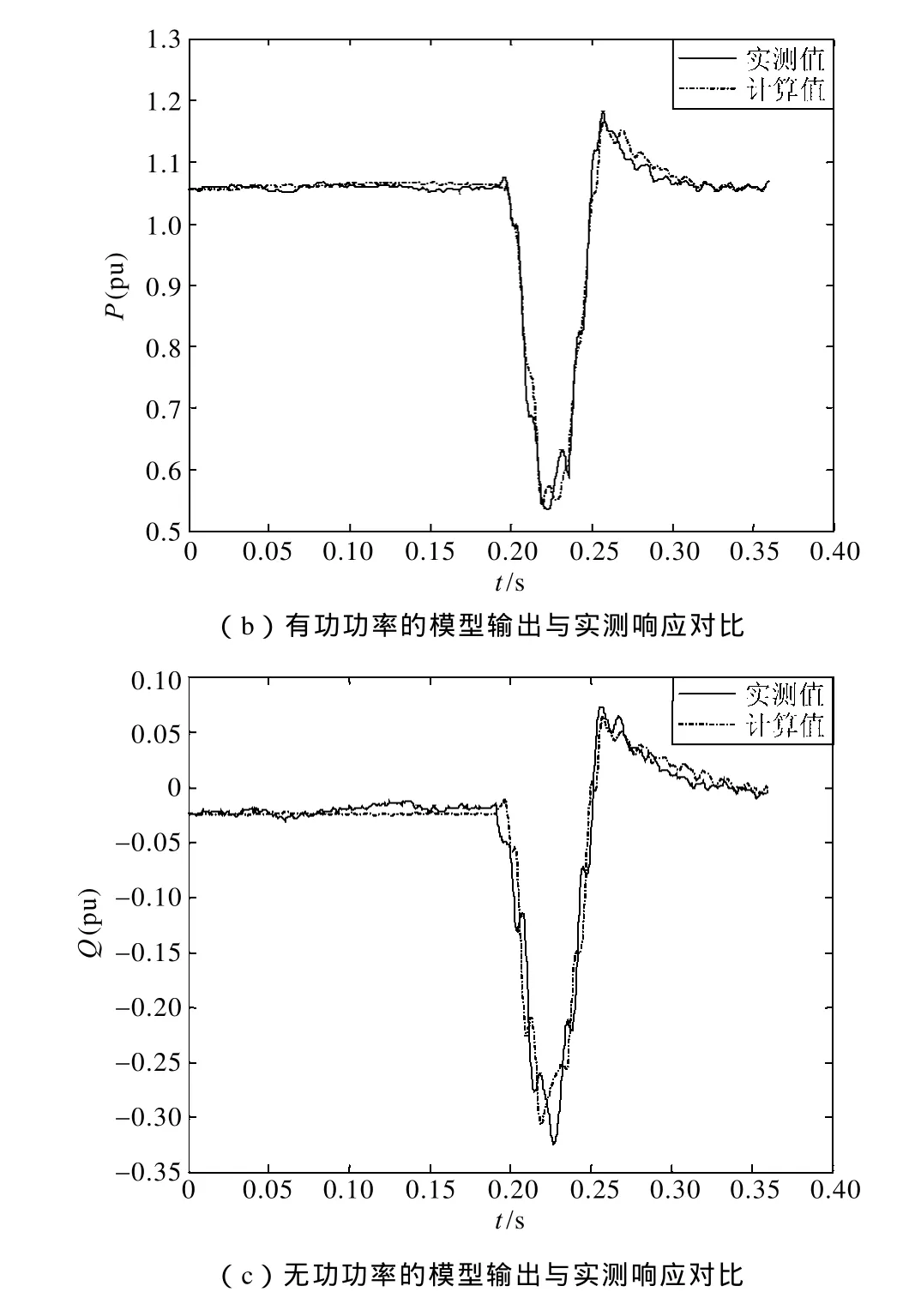
图3 模型响应与实测响应对比Fig.3 Comparison between load model output and measured data

由图3可以看出，辨识得到的负荷模型输出能够比较精确地拟合实测功率响应曲线。这说明采用CQDPSO算法辨识得到的负荷模型参数具有较高的精度。根据文献[28]，负荷模型可以利用相对误差进行评价；若相对误差小于 5%，则该负荷模型是可以接受的。相对误差ε可以通过公式（10）计算

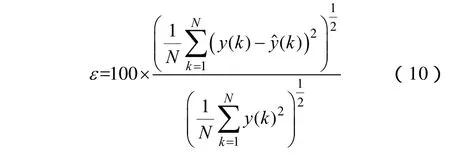
辨识得到的负荷模型参数见表1。

为了比较CQDPSO算法、QDPSO算法和PSO算法的性能，取粒子数为60，迭代次数为50，分别采用三种方法对算例中的模型参数辨识50次。

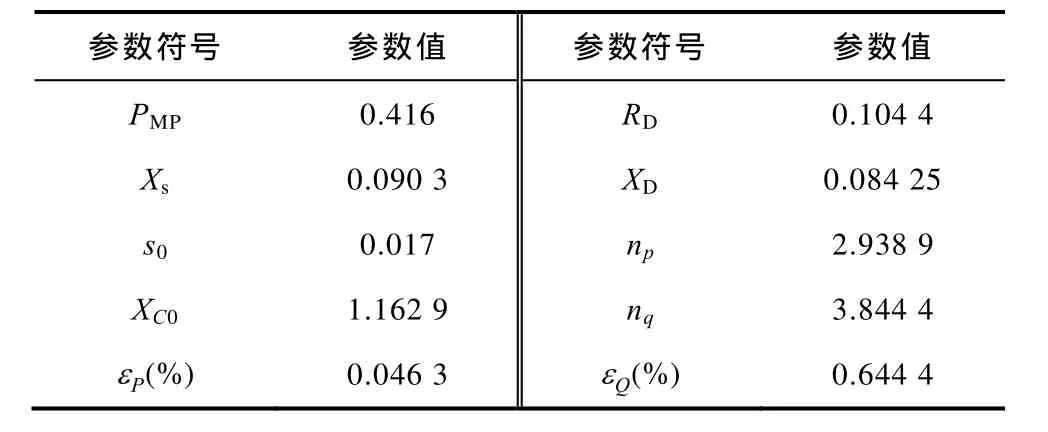
表1 参数辨识结果及相对误差Tab.1 Parameter identification results and relative errors

然后，利用式（11）计算50次辨识过程中的平均最优位置（mBest）。

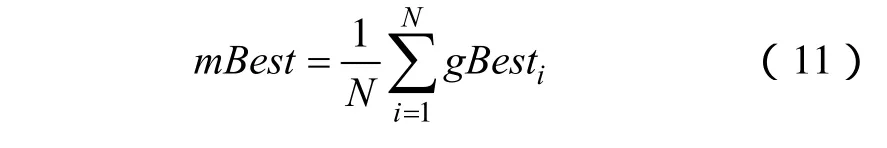
平均最优位置反映了全局最优值在迭代过程中的平均变化规律，能够反映算法的收敛特性。三种算法的平均最优位置变化如图4所示，辨识结果的误差平均值见表2。

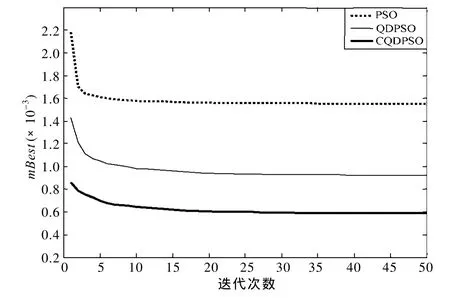
图4 三种算法的平均最优位置Fig.4 Mean best position of the three algorithms

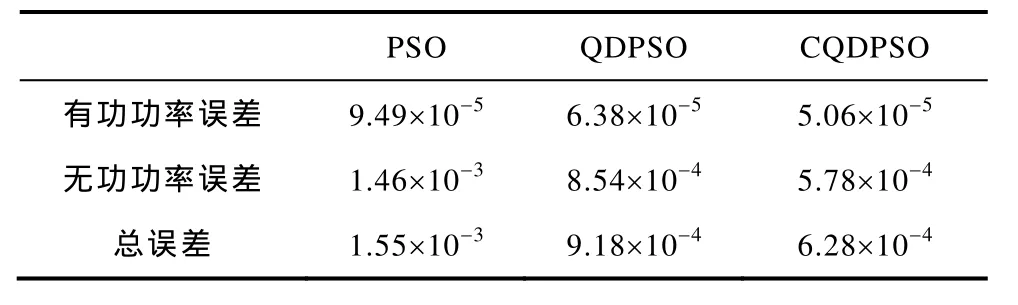
表2 三种算法的对比结果Tab.2 Comparison results of the three algorithms

从图4可以看到，PSO算法虽然收敛速度很快，但容易陷入局部收敛；CQDPSO算法和QDPSO算法分别需要约27次和38次迭代才能收敛到稳定值，而且相对于QDPSO算法，CQDPSO算法的收敛精度更高，这说明CQDPSO算法具有收敛速度快和收敛精度高的优点。从表2可以看出，无论是有功功率误差、无功功率误差还是总误差，CQDPSO算法的收敛结果的误差平均值均要比另外两种算法小，这进一步表明了 CQDPSO算法具有收敛精度高的优点。

5 结论

本文提出了利用 CQDPSO算法进行综合负荷模型参数辨识的方法。利用故障录波装置收集负荷特性数据，在此基础上，选取考虑配电网络的综合负荷模型并采用CQDPSO算法进行参数辨识，结果验证了 CQDPSO算法用于综合负荷模型参数辨识的有效性。与PSO算法及QDPSO算法进行对比表明，CQDPSO算法在收敛速度和收敛精度等方面均具有优势，将CQDPSO算法用于负荷建模能够提高负荷模型的准确性。

[1] Ma Jin, Han Dong, He Renmu, et al. Reducing identified parameters of measurement-based composite load model[J]. IEEE Transactions on Power Systems,2008, 23(1): 76-83.

[2] 王振树, 李林川, 牛丽. 基于贝叶斯证据框架的支持向量机负荷建模[J]. 电工技术学报, 2009, 24(8):127-134, 140.Wang Zhenshu, Li Linchuan, Niu Li. Load modeling based on support vector machine based on Bayesian evidence framework[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 127-134, 140.

[3] 汤涌, 张红斌, 侯俊贤, 等. 负荷建模的基本原则和方法[J]. 电网技术, 2007, 31(4): 1-5.Tang Yong, Zhang Hongbin, Hou Junxian, et al. Study on essential principle and methods for load modeling[J]. Power System Technology, 2007, 31(4): 1-5.

[4] Kosterev D N, Taylor C W, Mittelstadt W A. Model validation for the August 10, 1996 WSCC system outage[J]. IEEE Transactions on Power Systems,1999, 14(3): 967-979.

[5] Pereira L, Kosterev D, Makin P, et al. An interim dynamic induction motor model for stability studies in the WSCC[J]. IEEE Transactions on Power System,2002, 17(4): 1108-1115.

[6] Price W W, Wirgau K A, Murdoch A, et al. Load modeling for power flow and transient stability computer studies[J]. IEEE Transactions on Power Systems, 1998, 3(1): 180-187.

[7] Wang Zhenshu, Bian Shaorun, Liu Yan, et al. The load characteristics classification and synthesis of substations in large area power grid[J]. International Journal of Electrical Power & Energy Systems, 2013,48(1): 71-82.

[8] Lin Chia-Jen, Yung-Tien Chen, Chiou C Y, et al.Dynamic load models in power systems using the measurement approach[J]. IEEE Transactions on Power Systems, 1993, 8(1): 309-315.

[9] Liu Zhonghui, Wang Zhenshu, Su Meihua. Dynamic load modeling based on extreme learning machine[J].Applied Mechanics and Materials, 2012(195-196):1043-1048.

[10] 鞠平, 刘伟航, 项丽, 等. 电力系统负荷建模的自动故障拟合法[J]. 电力系统自动化, 2013, 37(10):60-64.Ju Ping, Liu Weihang, Xiang Li, et al. Automatic post-disturbance simulation based method for power system load modeling[J]. Automation of Electric Power Systems, 2013, 37(10): 60-64.

[11] Ping Ju, Chuan Qin, Feng Wu, et al. Load modeling for wide area power system[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(4):909-917.

[12] Abdelaziz A Y, Badr M A L, Younes A H. Dynamic load modeling of an Egyptian primary distribution system using neural networks[J]. International Journal of Electrical Power & Energy Systems, 2007 29(9):637-649

[13] Maitra A, Gaikwad A, Zhang P, et al. Using system disturbance measurement data to develop improved load models[C]. IEEE Power Systems Conference and Exposition, 2006: 1978-1985.

[14] Ren-Feng Yuan, Qian Ai, Xing He. Research on dynamic load modelling based on power quality monitoring system[J]. IET Generation, Transmission& Distribution, 2013, 7(1): 46-51.

[15] 王振树, 张波, 李欣唐, 等. 新型电力故障录波监测系统[J]. 电力系统自动化, 2007, 31(10): 92-96, 101.Wang Zhenshu, Zhang Bo, Li Xintang et al. A novel type of power fault recording and monitoring system[J]. Automation of Electric Power Systems, 2007,31(10): 92-96, 101.

[16] 仲卫进, 艾芊. 扩展卡尔曼滤波在动态负荷参数辨识中应用[J]. 电力自动化设备, 2007, 27(2): 47-50.Zhong Weijin, Ai Qian. Application of extended Kalman filter in parameter identification of dynamic load model[J]. Electric Power Automation Equipment,2007, 27(2): 47-50.

[17] 艾芊, 陈陈, 沈善德, 等. 简化前馈网络用于负荷模型参数辨识的研究[J]. 中国电机工程学报, 2005,25(5): 21-27.Ai Qian, Chen Chen, Shen Shande, et al. Research on parameter identification of load models by using liner BP networks[J]. Proceedings of the CSEE, 2005,25(5): 21-27.

[18] Hua Bai, Pei Zhang, Venkataramana Ajjarapu. A novel parameter identification approach via hybrid learning for aggregate load modeling[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1145-1154.

[19] 程颖, 鞠平, 吴峰, 等. 负荷模型参数辨识的粒子群优化法及其与基因算法比较[J]. 电力系统自动化,2003, 27(11): 25-29.Cheng Ying, Ju Ping, Wu Feng, et al. Ps algorithm in load parameter identification and its comparison with genetic algorithm[J]. Automation of Electric Power Systems, 2003, 27(11): 25-29.

[20] Van den Bergh F. An analysis of particle swarm optimizers[D]. Pretoria: University of Pretoria, 2001.[21] Jun Sun, Bin Feng, Wenbo Xu. Particle swarm optimization with particles having quantum behavior[C].Proceedings of the 2004 Congress on Evolutionary Computation, 2004: 325-331.

[22] Kou Pangao, Zhou Jianzhong, Wang Changqing, et al.Parameters identification of nonlinear state space model of synchronous generator[J]. Engineering Applications of Artificial Intelligence, 2011, 24(7): 1227-1237.

[23] Sun Jun, Fang Wei, Wu Xiaojun, et al. Qos multicast routing using a quantum-behaved particle swarm optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2011, 24(1): 123-131.

[24] Omkar S N, Khandelwal R, Ananth T V S, et al.Quantum behaved particle swarm optimization(QPSO)for multi-objective design optimization of composite structures[J]. Expert Systems with Applications, 2009,36(8): 11312-11322.

[25] 王爽心, 姜妍, 韩芳, 等. 一种综合负荷模型参数辨识的混沌优化策略[J]. 中国电机工程学报, 2006,26(12): 111-116.Wang Shuangxin, Jiang Yan, Han Fang, et al. A chaotic optimization strategy used in parameter identification of composite load model[J]. Proceedings of the CSEE, 2006, 26(12): 111-116.

[26] Leandro dos Santos Coelho. Tuning of PID controller for an automatic regulator voltage system using chaotic optimization approach[J]. Chaos, Solitons and Fractals,2009, 39(4): 1504-1514.

[27] 汤涌, 张红斌, 侯俊贤, 等. 考虑配电网络的综合负荷模型[J]. 电网技术, 2007, 31(5): 34-38.Tang Yong, Zhang Hongbin, Hou Junxian, et al. A synthesis load model with distribution network[J].Power System Technology, 2007, 31(5): 34-38.

[28] Byoung-Kon Choi, Hsiao-Dong Chiang, Yinhong Li,et al. Measurement-based dynamic load models:derivation, comparison and validation[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1276-1283.