基于等效间隔-频率分布的含风电场电力系统随机生产模拟

谈天夫 高 山 李海峰 罗建裕

（1. 东南大学电气工程学院 南京 210096 2. 江苏省电力公司 南京 210014）

1 引言

随着风电接入量的不断提高，在获得清洁能源相关效益的同时，其出力的间歇性和波动性对电力系统运行、规划等方面的影响日益突出，获得了广泛关注[1-3]。由于风电的随机波动性，系统面临的备用压力有所增大，同时为了满足备用及负荷的需要，常规机组在调度运行中的起停动作也更加频繁，这些都会带来相关生产成本的提高[4-6]。作为评价电力系统生产成本与可靠性的重要途径[7]，电力系统随机生产模拟计算中有必要对风电波动性带来的影响加以考虑，如果能在计算中对风电时序相关信息进行处理，将有助于风电波动性及相关成本的评价。

目前随机生产模拟方法主要分为仿真法和解析法两大类，仿真法以蒙特卡罗法为最多[8-11]，通过对负荷及间歇性电源的时序仿真，能较为方便地考虑其中的时序相关信息。解析法中能对时序相关信息进行处理的主要有两种：一为基于时序负荷曲线的生产模拟方法，由于直接采用时序负荷曲线进行计算，保留了时序相关信息并可在计算中考虑其影响[12,13]。二为基于频率持续法的相关随机生产模拟方法，通过负荷频率曲线，能对时序相关信息进行较多的考虑[14-18]。其中，文献[17,18]将频率持续法与等效电量函数法相结合，能对负荷及风电出力时序波动下的可靠性、燃料成本、动态成本等进行较为有效的评价。

频率持续法及其采用的负荷频率曲线反映了随机生产模拟中时序波动的频率信息部分，但同时忽略了时序波动的其余信息，导致在评价机组起停次数及相关动态成本时，发电机在短时间内的一些频繁起停也被计入其中，这与实际运行情况不符。为了更加全面地反映时序相关信息，本文引入负荷超越的间隔-频率分布（下文中简称为间隔-频率分布）概念，作为负荷频率曲线的一种扩展，由间隔-频率分布组成的间隔-频率分布族不仅包含了负荷频率曲线所含的所有信息，而且能一定程度地反映时序波动的时间分布信息，从而对机组起动次数等指标给出更加合理的评价。利用所提基于等效间隔-频率分布的随机生产模拟方法对EPRI 36机组系统进行计算，验证了所提方法的有效性。

2 基本原理

2.1 负荷频率曲线

时序波动相关信息既包括波动的频率，也包括波动的时间分布等其他信息，较为完整地反映这些信息，有助于相关现象的刻画与描述。随机生产模拟中的仿真法，尤其是采用序贯仿真的方法，在反映与处理这一类信息方面具有较大的优势，且容易实现，所以应用广泛。而在随机生产模拟解析法中，往往需要对其中的一些复杂因素进行简化，这导致了相关信息的丢失和评价结果的误差。

负荷频率曲线（Load Frequency Curve，LFC）反映了负荷在向上方向上超越某一负荷水平的平均频率[17]。图1反映了某典型日原始负荷变化、风电出力变化、以及净负荷变化。对于图中的原始负荷时序曲线，在7时，负荷为74MW，而在8时，负荷上升至86MW，则对于负荷水平80MW，就完成了一次向上方向上的负荷超越，对整个负荷时序曲线进行遍历，就可得到相应的负荷频率曲线，如图2所示。在频率持续法中，通过负荷频率曲线反映负荷的时序相关信息，通过该信息与机组的启、停产生对应关系，从而考察机组的起停、备用等动作及相关费用。在图1中，如果某台机组在负荷80MW处开始带负荷，则8时之前该机处于停机或热备用状态，8时之后处于开机状态，也就是说，这次负荷超越对应了一次开机过程，因而负荷频率曲线中的频率信息是衡量机组起停次数的重要依据。通过将初始负荷时序曲线与间歇性电源出力时序曲线直接相减，可得到净负荷曲线作为负荷频率曲线的生成依据，从而考虑间歇性能源的影响[17]。由于风电的加入，图1中的净负荷曲线与原始负荷曲线相比出现了更多的波动，在相应的负荷频率曲线上，负荷超越频率的总数显著增加，主要分布负荷区域也有所变化。

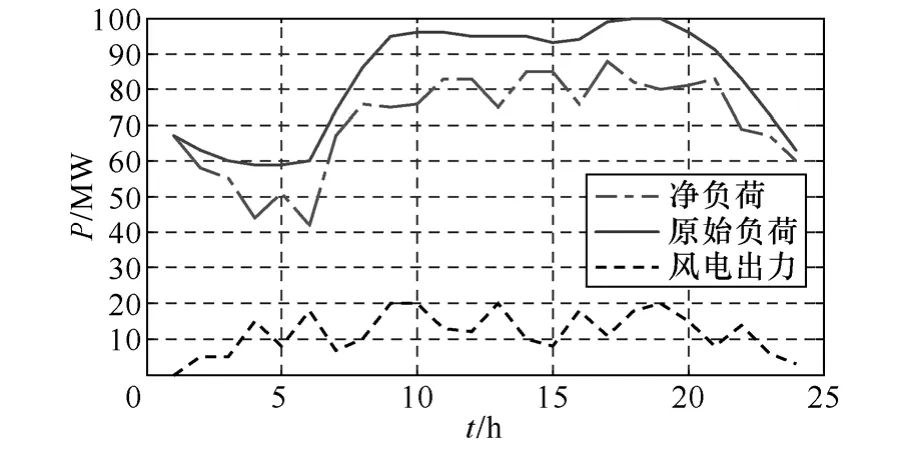
图1 原始负荷、净负荷与风电出力时序曲线Fig.1 Chronological original load，net load and wind output curve

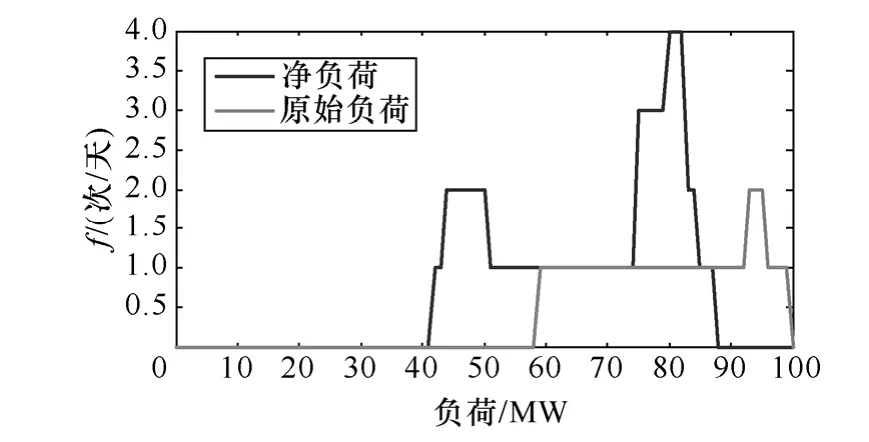
图2 负荷频率曲线Fig.2 Load frequency curve

对于某个负荷水平，相邻两次负荷超越之间存在着一定的时间间隔。在负荷水平80MW处，原始负荷曲线在8时完成了一次负荷超越，其与相邻负荷超越的间隔时间在8h以上。接入风电后，不仅波动的频率有所增加，而且波动的间隔趋于减小。同样以80MW负荷水平为例，净负荷曲线一共发生了4次负荷超越，分别在11时、14时、17时和20时，有三次负荷超越的间隔为3h，如果将负荷超越与开机过程一一对应，这意味着三次间隔时间3h的开机动作。如果该发电机的允许起动间隔时间较长，则其很可能会选择在一些时段保持压出力状态，而不是频繁起停，随着间歇性电源接入量和波动性的提高，这种情况可能会更加频繁地出现，仅仅依靠负荷时序波动的频率信息显得有所不足，需要通过更多的信息进行计算和评价。为此，通过将负荷频率曲线扩展为负荷超越的间隔-频率分布及间隔-频率分布族，同时反映时序波动的频率信息与时间分布信息，从而形成基于等效间隔-频率分布的随机生产模拟方法，对机组的起停次数及相关成本给出更加合理的评价。

2.2 负荷超越的间隔-频率分布

在波动的负荷下，对于某一特定的负荷水平，连续两次负荷超越之间的时间间隔表现为一定区域中的离散分布。

负荷超越的间隔-频率分布，反映的是在研究时间T内，负荷超越某一负荷水平的间隔时间分布。对于负荷频率曲线上的某一负荷水平 x，通过遍历负荷时序曲线，可以得到连续两次负荷超越时间间隔的分布，即形成负荷水平 x对应的间隔-频率分布。对于负荷频率曲线研究范围内的所有负荷水平，都可以形成相应的间隔-频率分布，从而得到与负荷频率曲线相对应的间隔-频率分布族，如图3所示。

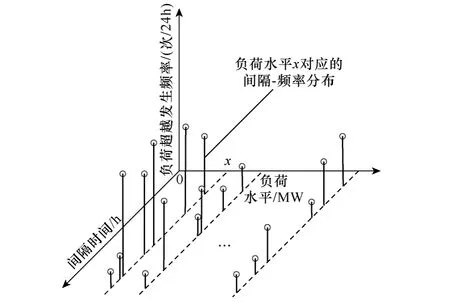
图3 间隔-频率分布族及负荷水平x对应的间隔-频率分布Fig.3 Interval frequency distribution series and interval frequency distribution for load level x

在离散情况下，假设间隔-频率曲线形成过程中的时间取值是步长为1的整数，单位为 h，负荷水平取值也是步长为1的整数，单位为MW，则负荷水平 k对应的间隔-频率分布可以表示为一个向量，其中，Tmax为考虑的最大时间间隔长度（h），为一设定值；kiα表示负荷水平k对应的间隔时间为i小时的负荷超越发生频率，文中将其归算至固定周期T=24h内。由于在实际计算中会出现负荷超越存在但间隔时间大于Tmax的情况以及负荷超越次数为 0（对应于间隔时间无限）的情况，将间隔-频率分布的向量表示扩充为和分别表示负荷水平k对应的间隔时间大于Tmax和无限的负荷超越发生频率。整个间隔-频率分布族可表示为一个由上述向量组成的矩阵，即

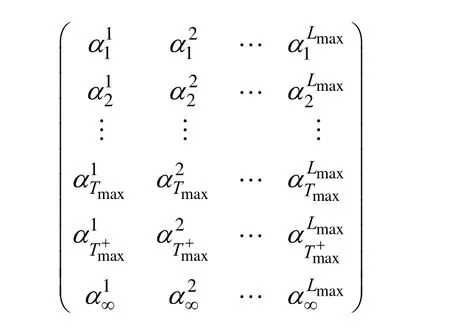
式中，Lmax为考虑的最大负荷水平，MW。

比较负荷频率曲线和间隔-频率分布族的定义可以发现，后者可以看成是前者的一种扩展，包含了前者的所有信息，负荷水平x对应的间隔-频率分布中，其所有间隔时间的负荷超越频率之和等于负荷频率曲线该负荷水平下的负荷超越频率。所以，通过间隔-频率分布族可以还原出负荷频率曲线。

2.3 等效间隔-频率分布的计算

等效间隔-频率分布族通过卷积考虑发电机的故障影响。在等效负荷频率曲线的卷积计算中，主要从负荷的时序波动和机组故障导致的额外起停两方面的影响进行考虑[14,17,18]，等效间隔-频率分布族的卷积过程也需要同时考虑上述两方面的影响。

2.3.1 时序波动影响的考虑

对于净负荷的时序波动影响方面，假设系统内有n台机组，安排第i-1台机组运行后的等效间隔-频率分布族为为负荷水平 x 对应的等效间隔-频率分布，在只考虑净负荷时序波动影响情况下，安排第i台机组运行后的等效间隔-频率分布族计算方法为

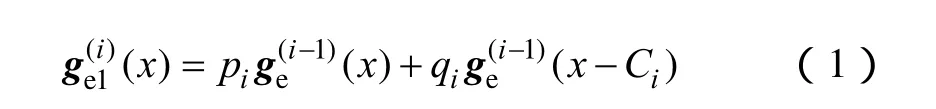
式中，qi为机组 i的强迫停运率，机组i的装机容量。

在2.2节假设的步长下，有

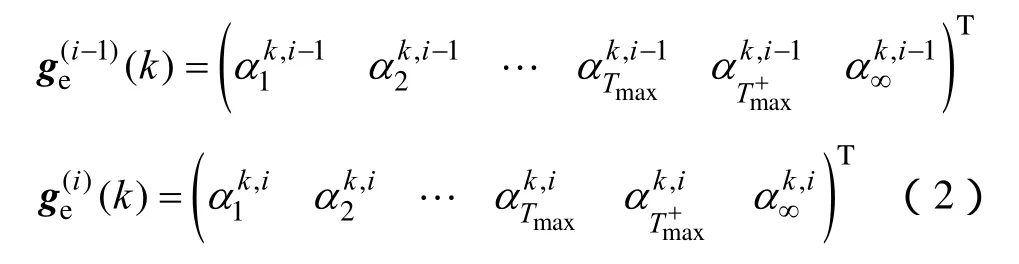
分别为间隔-频率分布族对应矩阵的一列。

式（1）可表示为

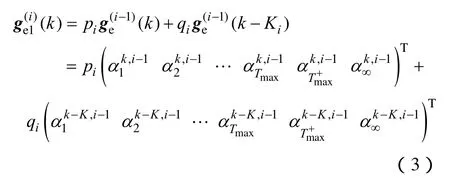
为间隔-频率分布族对应矩阵列之间的加权运算，Ki为Ci对应的步数。

2.3.2 机组故障导致额外起停影响的考虑

机组故障会导致等效负荷发生跃增，这一过程可能会导致某些负荷水平上发生额外的负荷超越，而这些额外的负荷超越意味着相应发电机额外的起停操作，所以，在等效间隔-频率分布族计算中需要对这一方面的影响加以考虑。

由于第i台机组的故障，对应于负荷水平x，期望增加的负荷超越次数可以表示为

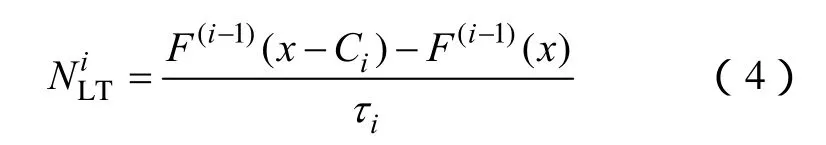
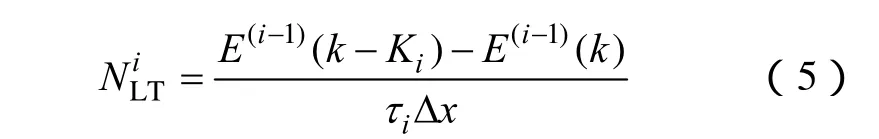
机组故障是随机发生的，在其带来一次额外的负荷超越时，会导致原有的负荷超越时间间隔发生变化，表现为某个包含该次负荷超越的时间间隔被分割成两个更小的间隔，而分割的发生和分割位置是随机的。所以，上述负荷超越次数的额外增加对负荷超越时间间隔的影响表现在间隔被分割后的重新分布，如某一长度为 t的时间间隔被分割后就变为两个单独的时间间隔t1、t2，且t1+t2=t。一个较长的时间间隔被分割后，会以不同的概率得到一系列长度较小的间隔。

由于分割过程不会改变期望的负荷超越次数增加量，且不会增加总的时间长度，在 2.2节的离散表示下，分割后的分布满足以下条件：

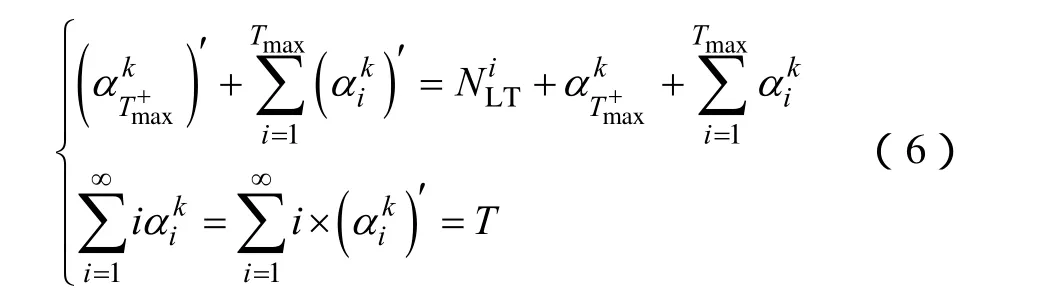
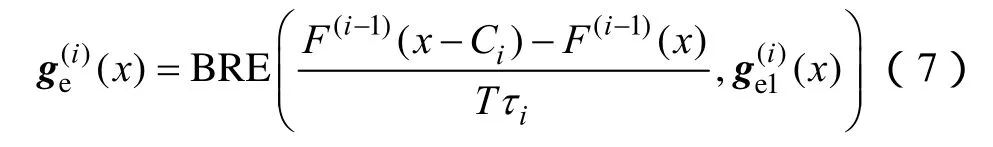
在离散情况下，式（7）可表示为

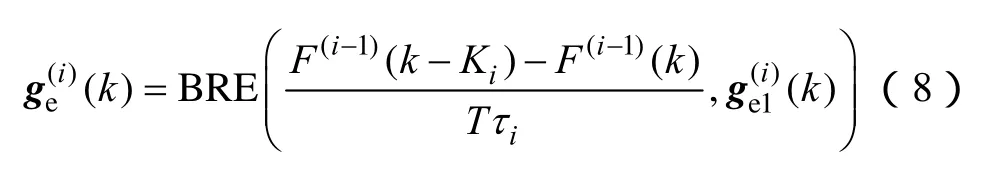
如结合等效电量函数法进行计算，式（7）可进一步表示为

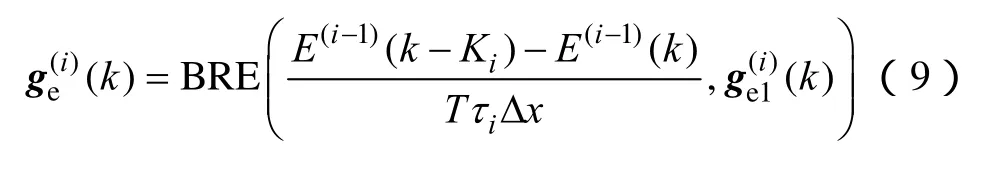
2.3.3 间隔分割的计算

由于间隔-频率分布族在实际计算中表示为离散的数组形式，这里给出BRE(·)在离散表示下的一种计算方法，该方法假设时间间隔的每个离散时段以相同概率发生分割，从而得到新的时间间隔分布。

（1）对于长度为i≤Tmax的间隔，其分割后生成长度为j＜i间隔的概率为j=i间隔的概率为，其中，pbre为单时段内的分割发生概率，

（2）对于长度为无限的间隔，也就是不发生负荷超越的情况，在分割后同样会得到一系列有限长度的分布。折算至单位时间内，其分割后生成长度为j的间隔概率为，折算至时段T内，概率为，而因为无限长段在发生分割后继续存在的概率为0，其本身概率在分割后为0。

（3）对于长度＞Tmax的间隔，由于不确知其长度，难以确切反映其对长度 1 ～Tmax的间隔概率的影响，因服从时段长度与频率的加权和为 T，所以在时可以计算得到等效的＞Tmax时段长度为

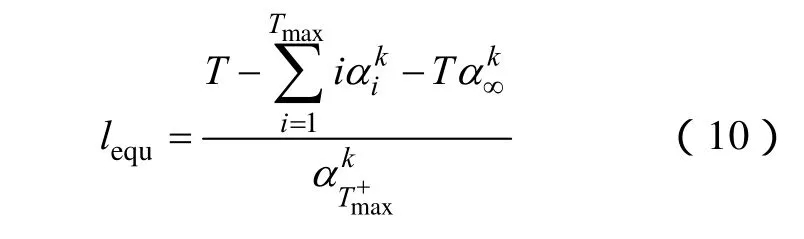
在得到分割后长度1～Tmax的间隔频率结果后，可以通过式（6）计算得到长度＞Tmax的间隔发生频率。对分割计算的流程如图4所示。

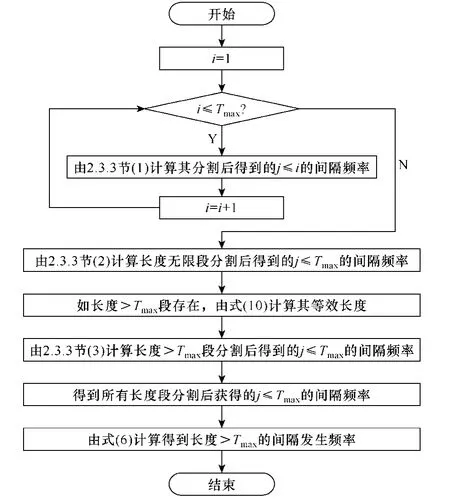
图4 间隔-频率分布分割计算流程Fig.4 Flow chart of break calculation of Interval frequency distribution

可以看到，机组故障影响导致的分割计算首先影响的是负荷超越的总频率，且这是一个确定的数值；其次会影响负荷超越间隔的分布，从而对机组起动相关评价结果产生影响。

2.4 机组开启次数及相关指标计算

负荷超越可以反映对发电机的起动需求，但是由于实际运行中发电机的起动受到负荷水平、发电机状态及最小起停时间、调度方式等多种因素共同影响，是一个相对复杂的决策结果，发电机的起动次数难以通过负荷超越次数来精确获得，只能作出一个总体的评价。

受到发电机最小运行时间和最小停运时间的限制，发电机两次起动的时间间隔不得低于其最小运行时间与最小停运时间之和。将发电机最小运行时间与最小停运时间之和设为该发电机的最小起动间隔时间，并将其作为负荷超越反映的发电机起动需求的可响应判断依据，只认为间隔大于等于该最小起动间隔时间的起动需求会得到响应。

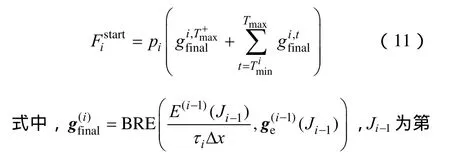
按照上述方法，第i台机组T时间内总的起动次数计算方法为i台机组的加载位置，Ji-1=，xi-1为已加载的前i-1台机组的总容量，为间隔长度为t的负荷超越频率，为间隔长度大于Tmax的负荷超越频率，为第i台机组的最小起动间隔时间。

为综合评价机组起停次数的变化，采用机组单位容量起停频率指标对发电机起动频率进行评价：

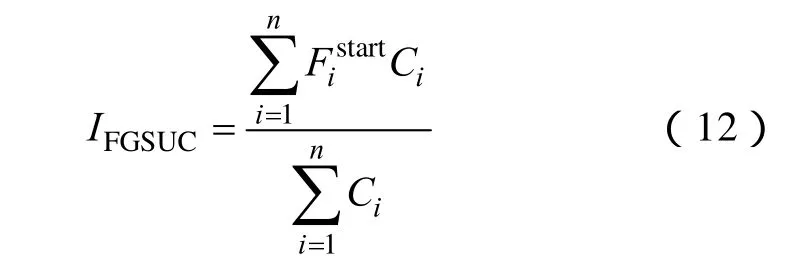
2.5 动态成本及相关指标计算

机组起停操作对应了发电成本中的动态费用，在含风电生产成本计算中，动态费用在总成本中占有明显的比例，有必要对其进行考虑，具体计算方法如下[18]。

动态费用主要包括锅炉起动费用 CBSU和汽轮机起停费用CTSU，即

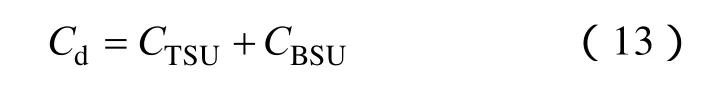
汽轮机起停费用CTSU

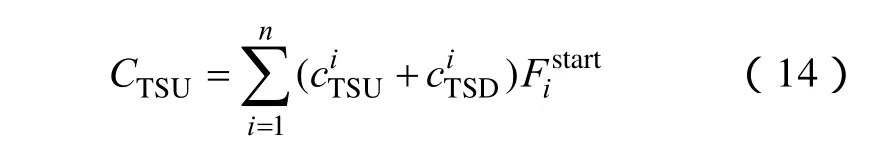
锅炉起动费用CBSU

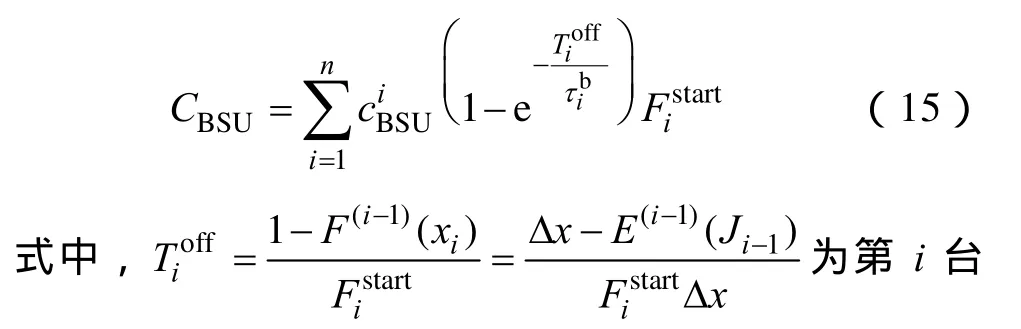
为了较为全面地评价短时间间隔时序波动的影响，同时提出短时间间隔动态费用（Short Time Interval Dynamic Cost, STIDC）指标ISTIDC、机组单位容量短时间间隔时长比例（Short Time Interval Proportion of Unit Capacity, STIPUC）指标ISTIDC。ISTIDC和基于等效间隔-频率分布计算，分别从费用和时间两个角度反映短时间间隔时序波动的影响，具体为

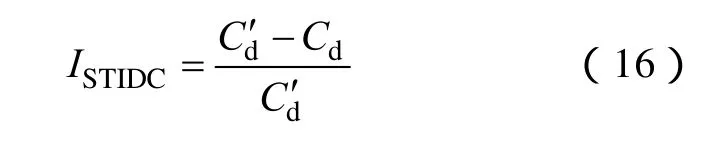
式中，Cd'为考虑所有时间间隔长度的发电机起动需求时得到的动态费用，其对应的发电机起动次数由等效间隔-频率分布族与等效负荷频率曲线的关系可知，Cd'相当于频率持续法的计算结果。

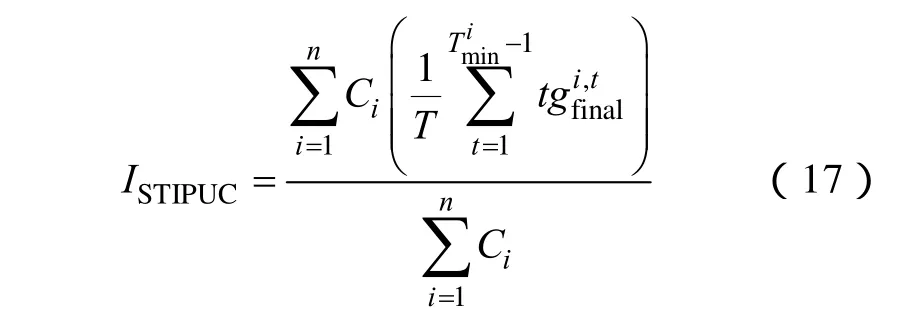
3 计算流程

基于等效间隔-频率分布的随机生产模拟算法采用图5所示流程，等效电量函数法计算在该流程中同步进行。

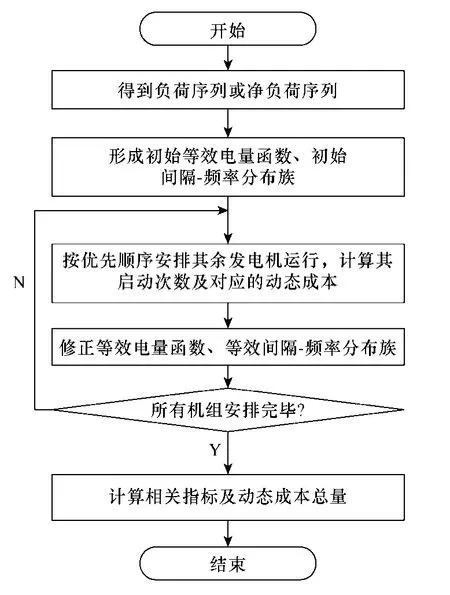
图5 算法流程图Fig.5 Flow chart of the algorithm

4 算例

算例采用EPRI 36机组系统，发电机参数及加载优先顺序由文献[17]数据补充获得，具体见表1，总装机容量为8 800MW。文中通过净负荷时间序列形成初始间隔-频率分布，因而需要以时间序列数据表示负荷及风电场出力。负荷时间序列数据参照IEEE RTS负荷数据[21]，年最大负荷8 502MW，模拟时间为一月份前30天（720h）；风机参数见表2，风速时间序列采用某风电场 30天历史数据，Tmax值取 30h，风电场出力时间序列通过结合风机故障仿真和风速历史数据获得，先通过仿真形成可用机组数的时间序列，再将其与风速历史数据及风机出力特性结合，得到风电场出力时间序列；将风电场出力时间序列与原始负荷时间序列相减，可得到考虑风电后的净负荷时间序列。

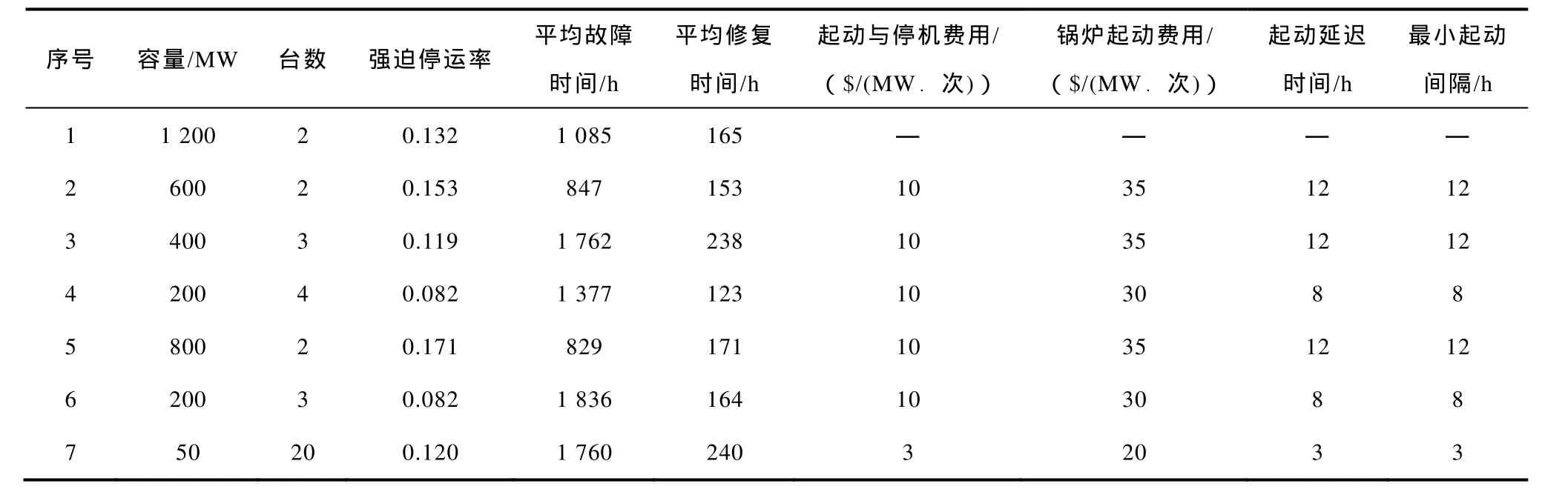
表1 发电机组数据Tab.1 Generator units data

表2 风机参数Tab.2 Data of the wind generator

图6所示为不含风电情况下所提方法计算结果还原的最终负荷频率曲线及通过频率持续法得到的最终负荷频率曲线，可以看到，两条曲线高度重合，这表明等效间隔-频率分布族可以准确还原出负荷频率曲线，其包含负荷频率曲线的所有信息。

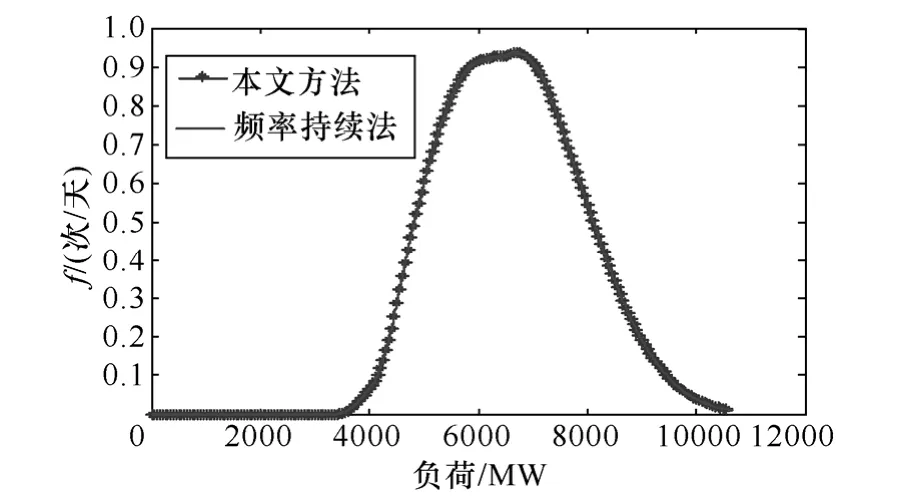
图6 最终负荷频率曲线Fig.6 Result of load frequency curve

图 7所示为不含风电和接入1 000台风机情况下，7号发电机加载对应负荷水平（4 400MW）的等效间隔-频率分布，该机最小起动间隔时间为12h。可以看到，在接入风电以后，间隔时长＜12h和≥12h的负荷超越数量均有明显增加，负荷超越总数增加显著。这表明，风电的波动性不但对发电机产生了更多的起停需求，同时也增加了许多不可能实现的起停需求，从而在计算评价中需要剔除这部分起停需求的影响。

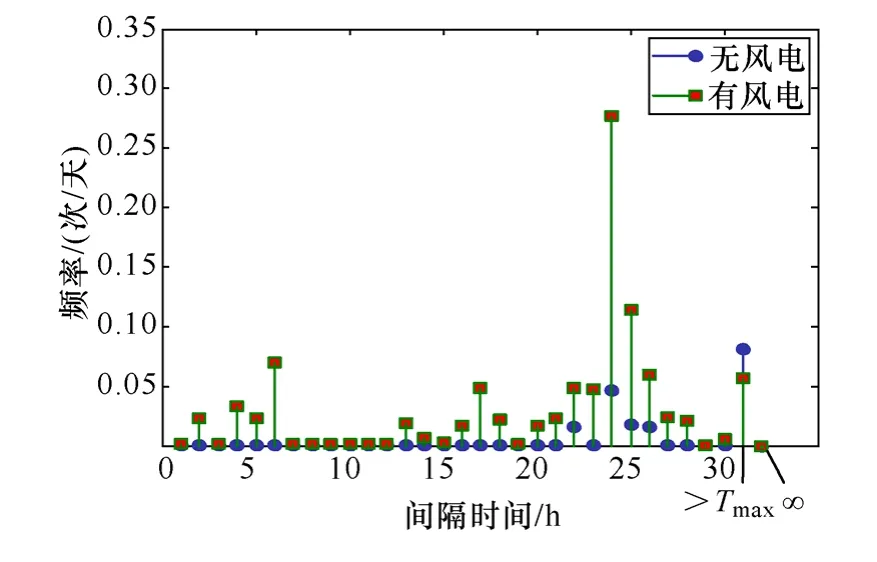
图7 负荷4 400MW处有风电和无风电时的等效间隔-频率分布Fig.7 Equivalent interval frequency distribution at 4 400MW with and without wind power

表3给出了不含风电和接入1 000台风机情况下，本文所提方法与频率持续（Frequency and Duration，FD）法、序贯蒙特卡洛仿真法（Sequential Monte Carlo Simulation，SMCS）的动态费用与IFGSUC指标计算结果。可以看到，相比不含风电的情况，这两个指标均有所增加；同时，由于计算中通过负荷时序波动的时间分布信息忽略了部分时间间隔过小的发电机起动需求，相较于频率持续法的计算结果，本文所提方法计算得到的指标数值相对较小，在两种情况下，动态费用分别相差8.5%和11.8%，IFGSUC分别相差12.4%和15.8%；与仿真法计算结果比较可以发现，相较于频率持续法，所提方法对发电机起停次数的评价结果明显更接近仿真法，由于与实际停机时间的误差，动态费用评价值仍有较大误差，但相比频率持续法有明显改善。

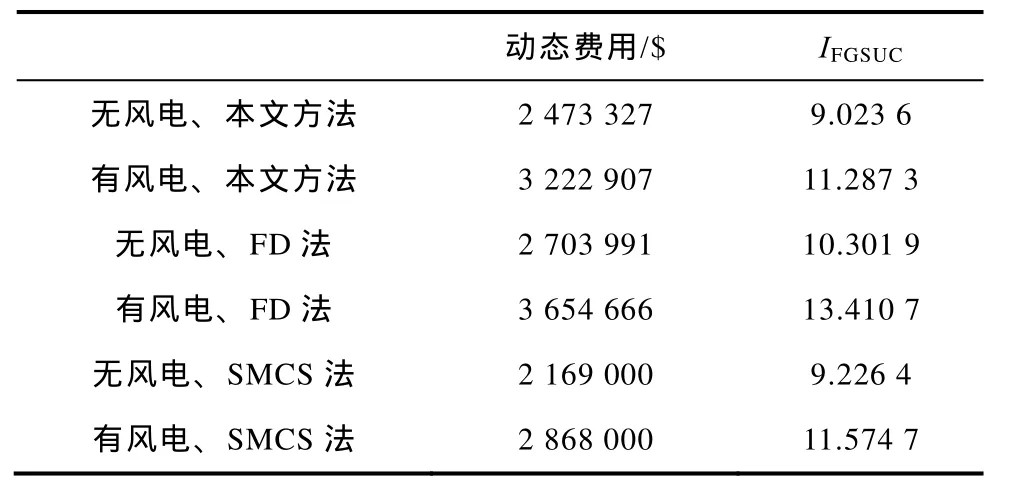
表3 随机生产模拟结果Tab.3 Probabilistic production simulation results

为进一步考察风电接入容量变化对算法结果的影响，比较风机接入数量为0～1 500台时本文所提方法对指标的评价结果，以及所提方法与频率持续法下动态费用计算结果的绝对差值。

式中，Cd1为所提方法得到的动态费用；Cd2为频率持续法得到的动态费用。

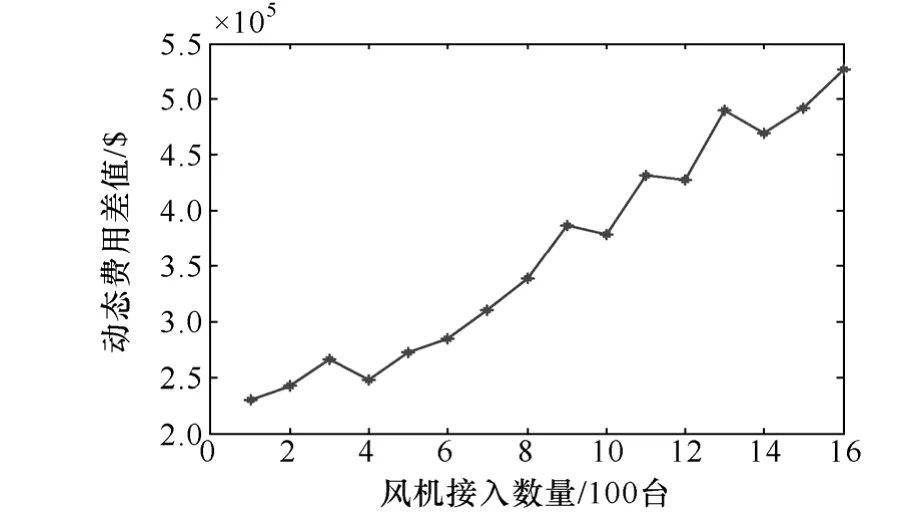
图9 动态费用差值-风机接入数量变化Fig.9 Difference of dynamic cost with different wind penetration

同时，图中存在局部的指标随风电接入量增加下降的现象，这主要由波动分布变化及各发电机加载对应的负荷水平造成，随着风电接入量增加，波动最强的负荷水平区间会发生变化，从而相应的发电机起动需求数量也会随之发生变化。

由于Tmax确定了算法中考虑的间隔时间长度上限，所以其大小可能对计算结果存在一定的影响。通过改变Tmax的数值，对计算结果进行比较，结果表明，Tmax从 13～720的变化并未导致计算结果的明显差异，而小于13则会导致结果的明显变化（系统中发电机的最小起停间隔为 3～12h）。这主要是由单位时间长度的分割概率 pbre较小所致，据此认为，Tmax可以采用一个较小的取值，但必须以发电机最小起动间隔的最大值为参照。

5 结论

本文通过引入负荷超越的间隔-频率分布概念，使随机生产模拟解析法中能同时考虑负荷时序波动的频率信息与时间分布信息，从而在考虑负荷及风电波动性的情况下，获得更加合理的机组起动次数、动态运行成本等指标。

算例表明，间隔-频率分布族包含了负荷频率曲线的所有信息，是后者的一种扩展。与频率持续法的计算结果相比，本文所提方法得到的动态费用及起停次数指标相对较小，反映了与短时间间隔分布时序波动相关的部分短时间间隔发电机起动需求被剔除后的评价结果差别，其在数值上更加接近仿真法的计算结果。

随着风电接入量的增加，其带来的波动性影响进一步增大，短时间间隔分布时序波动对相关指标的影响也将更加显著，值得在生产成本评价中加以考虑。作为一种专门的动态成本评价方法，本文所提方法可与其他随机生产模拟方法结合应用，对生产成本进行综合评价。

在实际运行中，除了负荷及风电的时序波动，调峰调频机组在调度中的作用也会对电力系统的运行效益造成影响，如果能进一步在随机生产模拟解析法中考虑这些因素的影响，其分析结果将更具客观性，在后续的研究中，将对此进行重点考虑。

[1] 胡国伟, 别朝红, 王锡凡. 考虑运行可靠性的含风电电力系统优化调度[J]. 电工技术学报, 2013,28(5): 58-65.Hu Guowei, Bie Zhaohong, Wang Xifan. Optimal dispatch in wind integrated system considering operation reliability[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 58-65.

[2] 张宁宇, 高山, 赵欣. 一种考虑风电随机性的机组组合模型及其算法[J]. 电工技术学报, 2013, 28(5):22-29.Zhang Ningyu, Gao Shan, Zhao Xin. An unit commitment model and algorithm with randomness of wind power[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 22-29.

[3] 袁建党, 袁铁江, 晁勤, 等. 电力市场环境下大规模风电并网系统电源规划研究[J]. 电力系统保护与控制, 2011, 39(5): 22-26.Yuan Jiandang, Yuan Tiejiang, Chao Qin, et al. Study of generation expansion planning of the power system incorporating large-scale wind power in the environment of electricity market[J]. Power System Protection and Control, 2011, 39(5): 22-26.

[4] 雷亚洲, 王伟胜, 印永华, 等. 风电对电力系统运行的价值分析[J]. 电网技术, 2002, 26(5): 10-14.Lei Yazhou, Wang Weisheng, Yin Yonghua, et al.Analysis of wind power value to power system operation[J]. Power System Technology, 2002, 26(5):10-14.

[5] 鲍爱霞. 大规模风电场容量可信度的分析及对华东电网备用的影响[J]. 中国电机工程学报, 2009,29(增刊): 34-38.Bao Aixia. Analysis and research for capacity credit of large scale wind farms and influence on reserve capacity of east china electric power grid[J]. Proceedings of the CSEE, 2009, 29(Sup.): 34-38.

[6] 柳进, 于继来, 柳焯. 针对风电间歇性扰动的旋转备用智能优化调度策略[J]. 中国电机工程学报,2013, 33(1): 163-170.Liu Jin, Yu Jilai, Liu Zhuo. An intelligent optimal dispatch strategy for spinning reserve coping with wind intermittent disturbance[J]. Proceedings of the CSEE, 2013, 33(1): 163-170.

[7] 王锡凡, 王秀丽. 随机生产模拟及其应用[J]. 电力系统自动化, 2003, 27(8): 10-15.Wang Xifan, Wang Xiuli. Probabilistic production simulation method and its application[J]. Automation of Electric Power Systems, 2003, 27(8): 10-15.

[8] Billinton R, Li W. A Monte Carlo method for multiarea generation system reliability assessment[J]. IEEE Transactions on Power Systems, 1992, 7(4): 1487-1492.

[9] 赵渊, 周家启, 刘志宏. 大电网可靠性的序贯和非序贯蒙特卡洛仿真的收敛性分析及比较[J]. 电工技术学报, 2009, 24(11): 127-133.Zhao Yuan, Zhou Jiaqi, Liu Zhihong. Convergence analysis and comparison of sequential and nonsequential Monte-Carlo simulation for bulk power system reliability assessment[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 127-133.

[10] 吴义纯, 丁明, 李生虎. 风电场对发输电系统可靠性影响的评估[J]. 电工技术学报, 2004, 19(11):72-76.Wu Yichun, Ding Ming, Li Shenghu. Reliability assessment of wind farms in generation and transmission systems[J]. Transactions of China Electrotechnical Society, 2004, 19(11): 72-76.

[11] 王剑, 刘天琪, 李兴源. 风电场及储能装置对发输电系统可靠性的影响[J]. 电网技术, 2011, 35(5):165-170.Wang Jian, Liu Tianqi, Li Xingyuan. Influences of connecting wind farms and energy storage devices to power grid on reliability of power generation and transmission system[J]. Power System Technology,2011, 35(5): 165-170.

[12] 夏清, 王少军, 相年德. 时序负荷曲线下电力系统概率性生产模拟[J]. 中国电机工程学报, 1994,14(3): 21-28.Xia Qing, Wang Shaojun, Xiang Niande. The probabilistic power system production simulation based on chronological load curve[J]. Proceedings of the CSEE,1994, 14(3): 21-28.

[13] 邹斌, 李冬. 基于有效容量分布的含风电场电力系统随机生产模拟[J]. 中国电机工程学报, 2012,32(7): 23-31.Zou Bin, Li Dong. Power system probabilistic production simulation with wind generation based on available capacity distribution[J]. Proceedings of the CSEE, 2012, 32(7): 23-31.

[14] Michael G. The inclusion of dynamic factors in statistical power system cost models, part I:assessment of start-up and banking costs[J]. IEEE Transactions on Power Systems, 1989, 4(2): 419-425.[15] Malik A S, Cory B J. An application of frequency and duration approach in generation planning[J]. IEEE Transactions on Power Systems, 1997, 12(3): 1076-1084.

[16] Malik A S. Simulating limited energy units within the framework of ELDC and FD methods[J]. Electrical Power & Energy Systems, 2004, 26(8): 645-653.

[17] 张节潭, 程浩忠, 胡泽春, 等. 含风电场的电力系统随机生产模拟[J]. 中国电机工程学报, 2009,29(28): 34-39.Zhang Jietan, Cheng Haozhong, Hu Zechun, et al.Power system probabilistic production simulation including wind farms[J]. Proceedings of the CSEE,2009, 29(28): 34-39.

[18] 曲翀, 王秀丽, 谢绍宇, 等. 含风电电力系统随机生产模拟的改进算法[J]. 西安交通大学学报, 2012,46(6): 115-121.Qu Chong, Wang Xiuli, Xie Shaoyu, et al. Improved algorithm for probabilistic production simulation of power systems with wind power[J]. Journal of Xi’an Jiaotong University, 2012, 46(6): 115-121.

[19] Wang X. Equivalent energy function approach to power system probabilistic modeling[J]. IEEE Transactions on Power Systems, 1988, 3(3): 823-829.

[20] 王锡凡. 电力系统随机生产模拟的等效电量函数法[J]. 西安交通大学学报, 1984, 18(6): 13-26.Wang Xifan. EEF approach to power system probabilistic modeling[J]. Journal of Xi’an Jiaotong University, 1984, 18(6): 13-26.

[21] The Reliability Test System Task Force of the Application of Probability Methods Subcommittee.IEEE reliability test system [J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(6): 2047-2054.