一种变压器时域场路耦合计算的自适应算法

潘 超 何雯婷 郝文波 徐冰亮

（1. 东北电力大学电气工程学院 吉林 132012 2. 黑龙江省电力科学研究院 哈尔滨 150030）

1 引言

变压器直流偏磁条件下的时域磁场计算以稳态电磁场分析为基础[1-3]，通常直接求解有限元微分方程，数据运算规模庞大，精确性较低[4,5]。文献[6,7]采用谐波平衡有限元法对单元内磁矢量位的各次谐波同时求解再叠加，结果具有较高的精确性；这种方法原理复杂，占用资源较多[8]。文献[9]通过计算分解的方法来优化资源，虽然减少了系统资源的占用率，但是计算时间较传统方法更长。基于电路-磁路耦合的方法能够反映出变压器直流偏磁时的励磁特性，满足工程分析需要，但是没有充分考虑漏磁情况，导致准确性降低[10]。场路耦合方法分为直接耦合与间接耦合两种方式，目前的大部分研究都采用直接方法实现场与路的耦合，将磁场方程与电路方程联立计算，效率较低[11]。上述方法大都建立二维模型模拟变压器铁心磁场分布，具有较高的精度，但二维场或对称场仅可作为局部场域的近似处理，只能用于特定运行方式或模型特性的分析，无法模拟变压器直流偏磁条件下的内部磁场分布[12]。这些问题在变压器等电磁设备的时域电磁计算中尤为突出，并亟需解决。

另一方面，传统时域计算通常采用单步低阶方法，其截断误差较大，且由于时间迭代造成误差累积，易引起求解振荡。若细化空间网格或缩短步长，虽然可以在一定程度上减小振荡，但计算规模会大幅度增加[13,14]。研究表明，变压器瞬态磁场和时域场路计算中均存在计算稳定性、效率及精确性的问题[15,16]。文献[17]讨论了变压器时域场路计算过程中非线性励磁、步长选择及时间离散在直流扰动下的变化情况。但是关于变压器时域场路耦合计算的稳定性、精度及效率等优化问题，目前罕有文献研究。

本文结合变压器直流偏磁问题，推导计算收敛时的稳定域边界，确定时间步长与计算稳定性的关系，研究变压器三维时域场路耦合计算效率与精确性的优化方法。根据稳定性分析提出一种自适应变步长算法，在计算效率和精确性方面与定步长算法对比，并通过实验测量对其计算结果进行验证。

2 时域场路耦合

利用时域场路耦合方法计算变压器磁场和等效电路，动态电感和时域电流为关键耦合参数，分别由三维棱边元磁场模型和等效电路模型计算。

建立变压器磁场模型，不考虑磁滞效应，棱边有限元法采用矢量磁位A，得到非线性磁场方程

变压器磁链方程

式中，ψ 为磁链向量；i为绕组电流向量；LS为静态电感矩阵，表示激励电流与磁链的稳态关系。

实际上，变压器励磁过程中电感与电流均体现出时变非线性的特点[18]。由u=dψ /dt，推导变压器等效电路的时域响应方程

式中，u为交流电压向量；UDC为直流电压；LD为考虑励磁变化的动态电感矩阵，需要通过磁场模型计算获得。

基于能量扰动的思想，根据系统能量变化计算动态电感参数。当线圈电流增加δip（0≤δ≤1，单相变压器中 1≤p≤2）时，将电源总能量与动态电感和电流关联，得到

若由电流增量δi引起的场量变化为δH、δB，变压器内部系统的磁场能量增量为

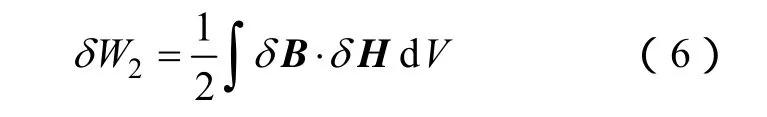
由能量平衡原理，方程（5）和（6）的能量相等，则可计算动态电感LD。

方程（4）的求解可采用四阶龙格库塔法，由tk时刻的线圈电流ik计算tk+1时刻ik+1

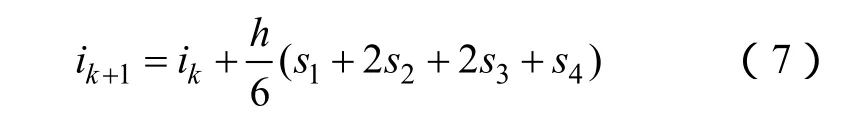
式中，h为步长；s1～s4为步长内的分段计算斜率。

利用绕组电流i与动态电感LD即可实现时域场路耦合，其迭代计算原理如图1所示。

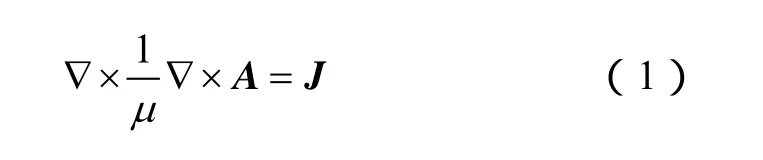
式中，μ 为磁导率；J为电流密度，需要通过电路模型计算得到。

应用格林定理，得伽辽金加权余量方程

式中，Mm为权函数序列，且权函数与基函数相同。

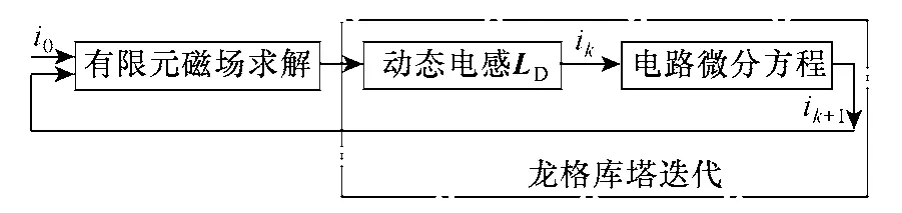
图1 时域场路耦合Fig.1 Time-domain magnetic field and electrical circuit coupling

3 自适应变步长算法

时域电路模型（4）的离散通解为式中，τ 为时间常数，取决于状态矩阵的特征值λmax，且τ =1/λmax。

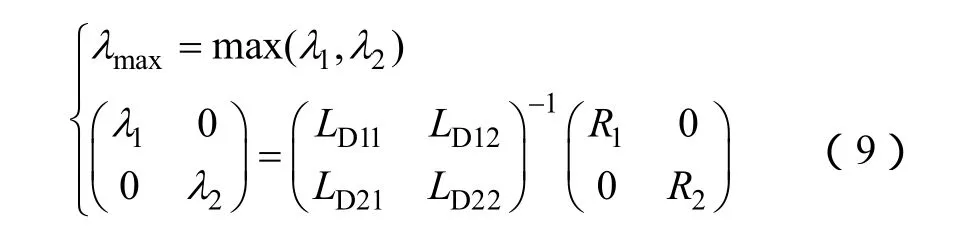
另一方面，在tk时刻式（4）中的泛函可化为常微分方程，得到式中，v为泰勒级数项的组合函数。

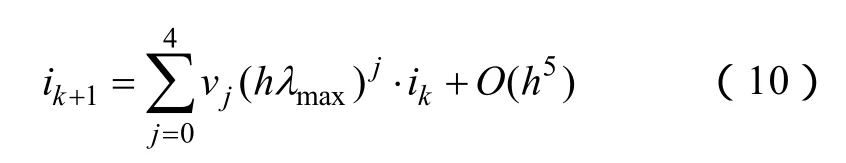
i(tk+1) 与 ik+1一致收敛到 h4阶，联立式（8）和式（10）有

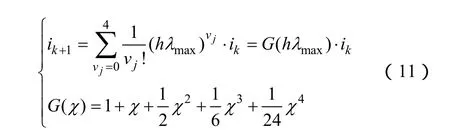
式中，G为传递函数；χ =hλmax。

时域场路耦合计算收敛所对应的绝对稳定域判据为│G│＜1。确定时域场路耦合计算的稳定边界为

式中，h0为稳定边界对应的计算步长。

对时域场路耦合迭代计算进行改进，提出一种自适应变步长算法，其基本原理为

（1）时域场路耦合计算受初值、步长等因素的影响，在起始阶段存在过渡过程，为了减少计算耗时，根据状态矩阵特征值，在计算稳定的前提下增大步长，从而提高效率。

（2）经过某段计算时间直至计算稳定时，在每次磁场求解动态电感之后，由变压器状态矩阵计算特征值，根据稳定域边界确定对应的h0，引入修正因子α(0＜α＜1)，确定下一时刻的计算步长，h=αh0，进行迭代计算。

（3）合理增大磁场计算的时间间隔，即降低磁场求解频率，增加电路迭代计算次数，w=βh0（80≥w≥40，β取整数），从而保证计算效率与精确性。

定义tk时刻的动态电感变化函数g(LD)，表示在该时间段内动态电感参数的变化速率，用来评价磁场计算的精确性。

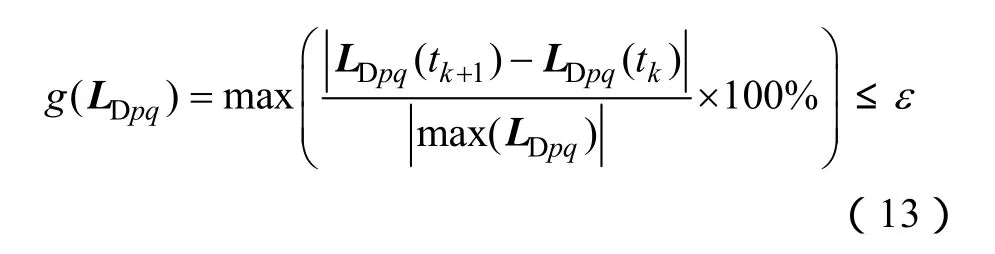
式中，max(LD) 为动态电感的最大值；ε 为变化率限值。

4 算例分析

采用时域场路耦合模型计算变压器直流偏磁问题，编译四阶龙格库塔法程序求解时域电路模型，利用Ansys软件建立变压器的八分之一模型（模型尺寸与实际比例为1∶1），对绝对稳定域边界和自适应算法进行研究分析。实验变压器型号为 BK300，如图 2所示，具体参数见表 1；铁心硅钢片型号为DW360—50，磁化曲线如图3所示。

图2 实验变压器Fig.2 Transformer for experiment

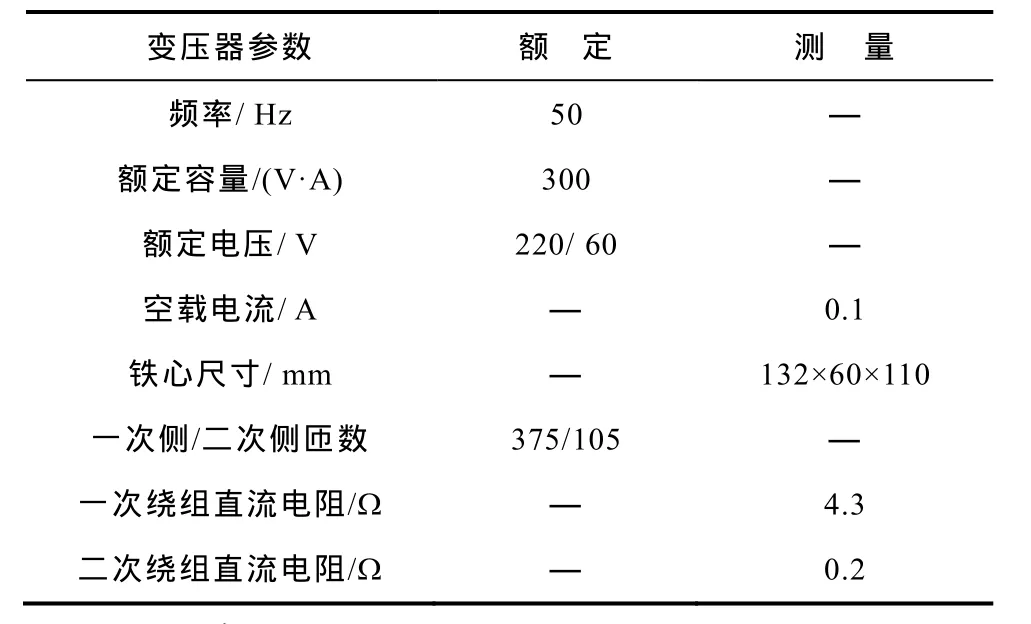
表1 变压器参数Tab.1 Parameters of transformer

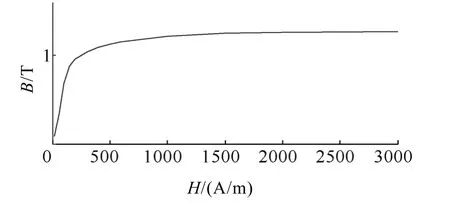
图3 铁心磁化曲线Fig.3 Magnetization curve of the core

4.1 时域场路耦合定步长算法

变压器一次侧空载电流峰值为Im，接入直流源UDC时的直流电流为 IDC。对空载运行 IDC=0、IDC=25%Im、IDC=50%Im、IDC=100%Im时的直流偏磁情况进行实验和仿真计算。无直流时，稳定边界对应步长 h0=6.0×10-4s，步长h取 5.0×10-4s时计算收敛；随着直流电流的升高，铁心励磁饱和程度加深，动态电感变化加剧，状态矩阵特征值增大，稳定性降低。当 IDC=50%Im时，h0=2.57×10-4s，h若取5.0×10-4s不满足稳定性要求；选取步长 h=2.50×10-4s，计算收敛。

分别采用基于时域场路耦合模型的定步长算法和自适应变步长算法进行计算，结果如图4所示。

图4 电流仿真计算和实验测量结果Fig.4 Results of currents of simulation and experiment

空载运行时一次电流 i1即为励磁电流 ie，由于磁场模型未考虑磁滞效应，根据 u→dψ/dt→dΦ/dt→B-H→i1的电磁耦合关系，i1为对称波，如图4a、图4b所示，两种方法计算的电流误差较小。当存在直流时，变压器励磁受直流水平影响，ie波形在正负半周不再对称，随着直流电流增大，变压器励磁饱和程度加深，ie波形畸变严重，正负半周的不对称程度加剧。由图4c可知，空载运行直流偏磁时电流的计算结果与实验测量基本相同；两者存在的误差可能由磁滞所导致，在直流偏磁情况下两者误差更小，从而验证了本文所提方法是正确可行的。

设计低通滤波和时域差分模块测量变压器瞬时电感波形，并与计算的动态电感对比，如图5所示。

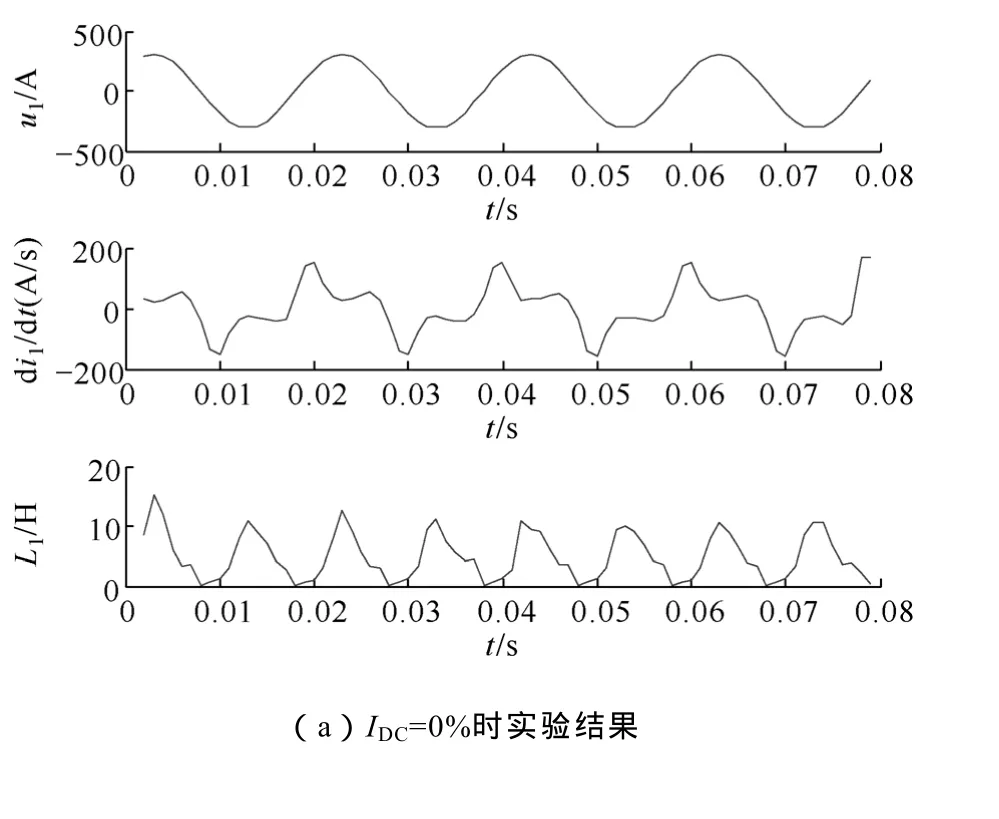
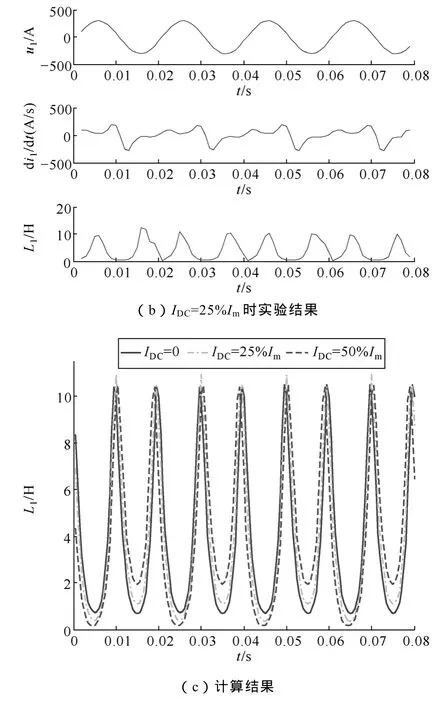
图5 动态电感Fig.5 Results of dynamic inductances of experiment and calculation

由图5可以确定动态电感变化与励磁非线性的对应关系。无直流时，L1在励磁的正负半周为对称波形，L1的波峰、波谷分别对应于励磁的非饱和状态与饱和状态。ie接近零值时，铁心励磁处于不饱和区，L1数值趋于最大；当ie趋于各半周内的极值时，铁心励磁饱和程度逐渐加深，L1数值趋于最小。当存在直流时，L1受直流水平影响，波形在正负半周不对称，随着直流电流增大，变压器励磁饱和程度加深，i1畸变严重，L1波形在正负半周的不对称程度加剧。为了便于对比，计算时采用单调双曲函数对磁化曲线进行拟合，图 5c的动态电感波形为固定步长计算结果，两种算法计算的电感在整体波形上并没有明显差异，因此这里不再给出。

变压器八分之一铁心模型磁场计算结果如图6所示。IDC=0时，铁心最大磁感应强度Bmax为1.24T，IDC=25%Im时，Bmax升至1.25T。通过计算可知，随着直流水平升高，变压器励磁饱和程度加深，铁心磁通密度增加。

图6 铁心磁场计算结果Fig.6 Magnetic distribution in iron core

采用定步长算法计算变压器正常运行，研究h、w对电感变化率和计算速度的影响。分析不同方案的计算稳定性、精确性及效率，结果见表2。

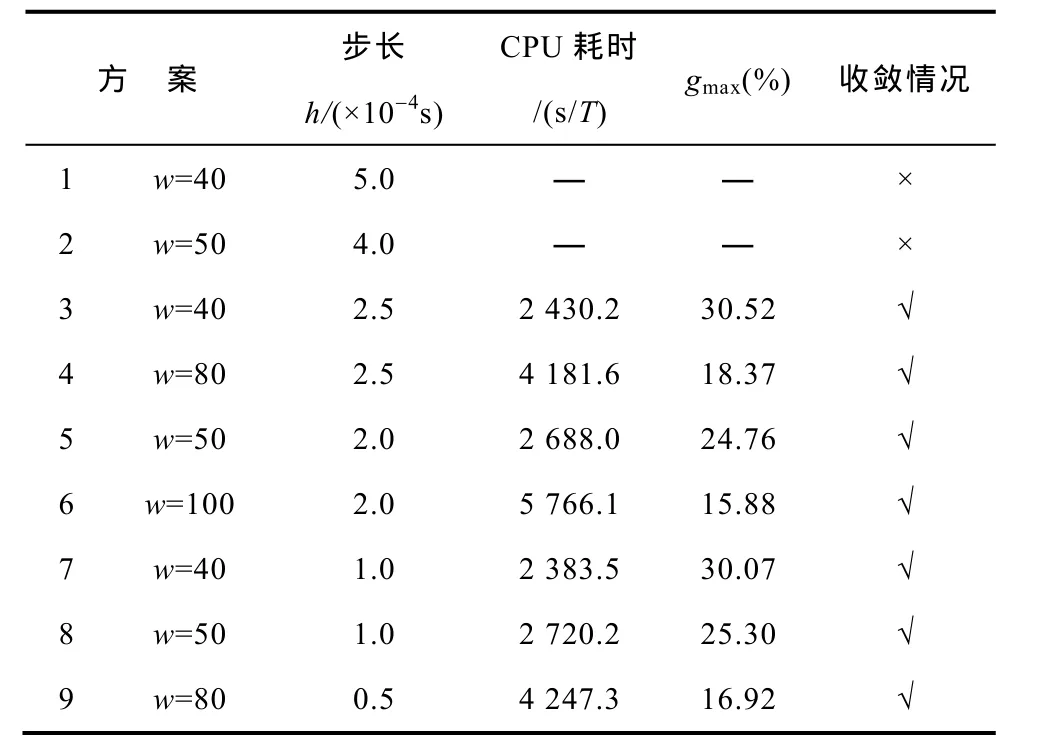
表2 定步长不同方案的计算结果Tab.2 Results of cases with fixed-step algorithm

变压器时域场路耦合计算过程中的电感参数具有时变性，导致励磁饱和时对应的稳定域边界较小。直流偏磁时随着直流分量增大，变压器励磁饱和程度加剧，对计算稳定性的要求也更为严格。当迭代计算的时间步长满足稳定域条件时，可以保证计算收敛，但是按该步长计算将占用较多资源和时间，效率较低。总结其规律，计算的稳定性由时间步长确定，满足绝对稳定域时，步长对计算效率和精确性的影响很小，此时效率和精确性主要取决于磁场的求解频率。不难看出，定步长算法在计算变压器非线性磁场时存在效率和精确性的优化问题。

4.2 自适应变步长算法

采用变步长算法进行计算，并与定步长算法的效率和精确性对比，结果见表3。

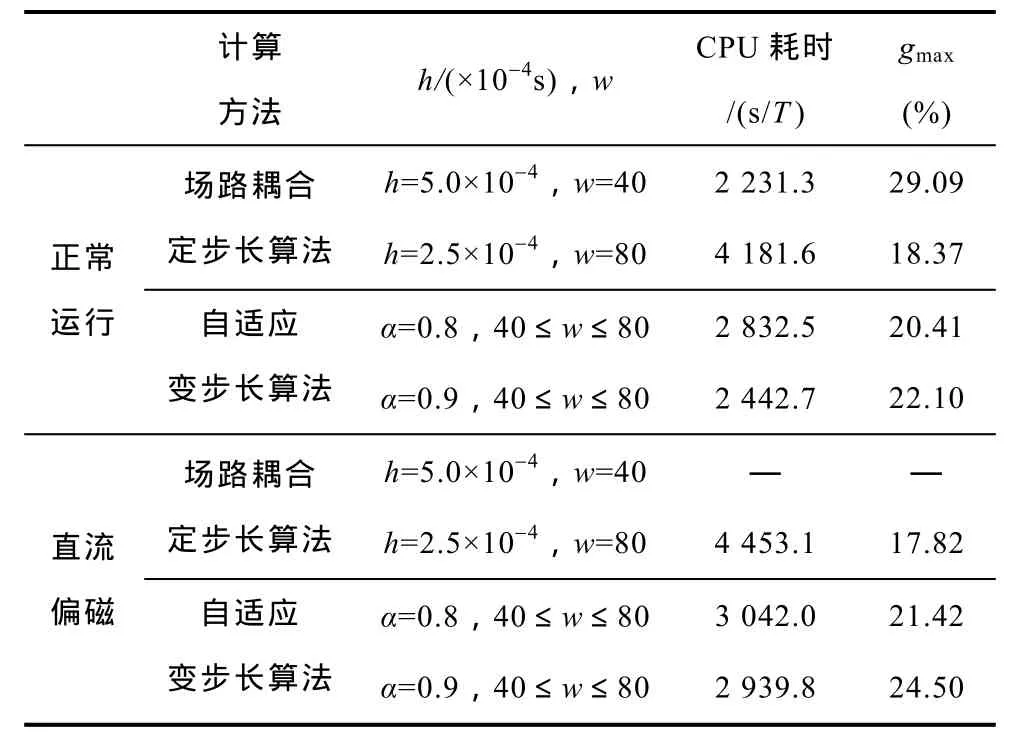
表3 不同方法的计算结果Tab.3 Results of different algorithms

结果表明，两种方法都能模拟变压器直流偏磁时的励磁过程。当时间步长选定为0.25ms时，虽然能够在一定程度上保证计算的稳定性和精确性，但是整个过程将会耗费大量时间。定步长算法虽然能够模拟变压器的励磁过程，但不能充分考虑其随时间变化的励磁特性，因此在计算时可能存在不收敛的问题；同时由于该算法的h和w固定，导致其计算效率和精确性无法改善。自适应变步长方法能够模拟变压器直流偏磁时励磁的时变非线性，时域计算每次迭代的h都能自动满足绝对稳定域边界，因此具有良好的计算稳定性；在此基础上合理选取 w能达到优化计算效率和精确性的目的。

对于实际工程中普遍关注的大型电力变压器直流偏磁问题，定步长算法可能受直流水平影响而不再适用，因而更能凸显出自适应优化算法的计算效率和精确性。目前作者还未能获取足够的实际数据以进行大型变压器的直流偏磁计算，因此该内容将是下一步研究的重点。

5 结论

结合变压器直流偏磁问题，基于时域场路耦合计算的稳定性分析提出一种自适应变步长算法，通过研究得出以下结论：

（1）变压器非线性励磁具有时变性，直流偏磁时励磁饱和程度加深，状态矩阵特征值增大，对应的稳定域边界变小。时域场路耦合计算时必须首先考虑稳定性问题，其计算步长应满足收敛条件，在此基础上合理选取磁场求解频率能够有效提高计算精确性和效率。

（2）与定步长时域场路耦合算法相比，自适应变步长算法计算变压器直流偏磁时能够有效模拟内部励磁的时变非线性，具有良好的计算稳定性，并能实现计算效率与精确性的合理优化。空载直流偏磁的电流计算结果与实验基本相同，验证了该方法的正确性。

[1] C M Liu, L G Liu, R Pirjola. Geomagnetically induced currents in the high-voltage power grid in China[J]. IEEE Transactions on Power Delivery, 2010,24(4): 2368-2374.

[2] 郭满生, 梅佳华, 张喜乐, 等. 直流偏磁条件下单相三柱电力变压器的损耗计算[J]. 电工技术学报,2010, 25(7): 67-71.Guo Mansheng, Mei Jiahua, Zhang Xile, et al.Calculation of losses in three phase limb transformer under DC-biasing[J]. Transactions on China Electrotechnical Society, 2010, 25(7): 67-71.

[3] 赵志刚, 刘福贵, 张俊杰, 等. 直流偏磁条件下变压器励磁电流的实验与分析[J]. 电工技术学报,2010, 25(4): 71-76.Zhao Zhigang, Liu Fugui, Zhang Junjie, et al.Measurement and analysis of magnetizing current in DC-biased transformers[J]. Transactions on China Electrotechnical Society, 2010, 25(4): 71-76.

[4] Lu Shu, Liu Yilu. FEM analysis of DC saturation to assess transformer susceptibility to geomagnetically induced currents[J]. IEEE Transactions on Power Delivery, 1993, 8(3): 1367-1376.

[5] Mauricio Valencia Ferreira da Luz, Jean Vianei Leite,et al. Three-phase transformer modeling using a vector hysteresis model and including the eddy current and the anomalous losses[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3201-3204.

[6] Zhao X J, Lu J W, et al. Analysis of DC bias phenomenon by the harmonic Balance Finite-Element method[J]. IEEE Transactions on Power Delivery,2011, 26(1): 475-485.

[7] Zhao X J, Li L, et al. Characteristic analysis of the square laminated core under dc-biased magnetization by the fixed-point harmonic-balanced FEM[J]. IEEE Transactions on Magnetics, 2012, 48(2): 747-750.

[8] Yamada R, Biringer P P, et al. Calculation of nonlinear eddy-current problems by the harmonic balance finite element method[J]. Transactions on Magnetics, 1991, 26(5): 4122-4125.

[9] 赵小军. 基于谐波平衡有限元的变压器直流偏磁特性研究[D]. 保定: 华北电力大学, 2010.

[10] 李泓志, 崔翔, 卢铁兵, 等. 变压器直流偏磁的电路-磁路模型[J]. 中国电机工程学报, 2009, 29(27):119-125.Li Hongzhi, Cui Xiang, Lu Tiebing, et al. Electric circuit and magnetic circuit combined model of DC biased power transformer[J]. Proceedings of the CSEE, 2009, 29(27): 119-125.

[11] 郭健, 林鹤云, 徐子宏, 等. 单螺旋绕组变压器支路电流的场路耦合计算及分析[J]. 电工技术学报,2010, 25(4): 65-70.Guo Jian, Lin Heyun, Xu Zihong, et al. Calculation and analysis of branch currents of single spiral winding transformer based on field circuit coupled method[J].Transactions on China Electrotechnical Society, 2010,25(4): 65-70.

[12] 潘超. 基于时域场路耦合模型的变压器直流偏磁电磁特性研究[D]. 保定: 华北电力大学, 2013.

[13] Shi Z W, Rajanathan C B. A method of approach to transient eddy current problems coupled with voltage sources[J]. IEEE Transactions on Magnetics, 1996,32(3): 1082-1085.

[14] D Rodger, N Allen. Calculation of transient 3D eddy currents in nonlinear media verification using a rotational test rig[J]. IEEE Transactions on Magnetics,1994, 30(5): 2988-2991.

[15] S L Ho, W N Fu. An incremental method for studying the steady state performance of induction motors using time stepping finite element model[J]. IEEE Transactions on Magnetics, 1997, 33(2): 1374-1377.

[16] S L Ho, S X Niu, et al. A power-balanced timestepping finite element method for transient magnetic field computation[J], IEEE Transactions on Magnetics,2012, 48(2): 291-294.

[17] 潘超, 王泽忠, 杨敬瑀, 等. 变压器直流偏磁瞬态场路耦合计算稳定性分析[J]. 电工技术学报, 2013,28(5): 82-87.Pan Chao, Wang Zezhong, Yang Jingyu, et al. Stability analysis based on transient magnetic-circuit coupled method for DC-biased transformer[J]. Transactions on China Electrotechnical Society, 2013, 28(5): 82-87.

[18] 王泽忠, 潘超, 周盛, 等. 基于棱边有限元的变压器场路耦合瞬态模型[J]. 电工技术学报, 2012,27(9): 146-152.Wang Zezhong, Pan Chao, Zhou Sheng, et al. Transient magnetic-circuit coupled model of transformer based on edge finite element method[J]. Transactions on China Electrotechnical Society, 2012, 27(9): 146-152.