测量控制网解算中两类观测值权的配比问题探讨

□ 侯利云 赵晓囡

（1.山西省测绘产品质量监督检验站，山西太原030002 2.太原理工大学测绘科学与技术系，山西太原030024）

1.引言

测量控制网在测量工作中应用十分广泛，外业观测以及数据预处理后，如何对观测数据进行快速而严密的处理，是广大测量工作者需要面对的一个重要问题。高金辉通过举例说明了在导线网平差中，当边、角权配比不当时，将影响最后的平差质量[1]。Helmert方差分量估计是解决这个问题的一种方法,其基本思想是通过不断的迭代平差来使得不同类型观测值的中误差趋向一致,从而达到最佳的平差效果。其缺点是原理深奥、计算复杂，实际计算中常常采用其近似公式计算[2]。为此，高金辉提出了一种简单易行的定权法——“逐次趋近法”，此法只要测角中误差确定较合理，就能取得与方差估计法相同的效果，且计算量小[1]；沙月进等人介绍了一种适用于两类不同观测值的“等价定权法”，计算简单，对于一般严密平差，平差精度理想[2]；刘长建等人提出了一种调整两类观测值权比的新方案，该方案是对方差分量估计的一个补充，通过固定正确的随机模型而仅仅调整不正确的随机模型，得到合理的结果[3]。

虽然许多学者对导线网平差过程中方差分量估计的应用做了进一步的研究，对其存在的不足做了一些补充[4-8]，但是测量控制网解算中两类观测值权的配比问题依旧缺少简单有效的方法。因此，本文通过算例说明，通过迭代使验后中误差与验前中误差近似相等，可以得到比较合理的平差结果。

2.材料与方法

如图1所示平面控制网。P1（X=4211916.408米，Y=554528.971米）和 P2（X=4209958.296米，Y=553938.346米）为已知点，P3、P4、P5和 P6为待定点，全网有 20个方向观测值（表1）和10个边长观测值（表2）。方向观测值的验前中误差为1.8秒，测距固定误差为2毫米，测距比例误差为3ppm。

图1 控制网略图

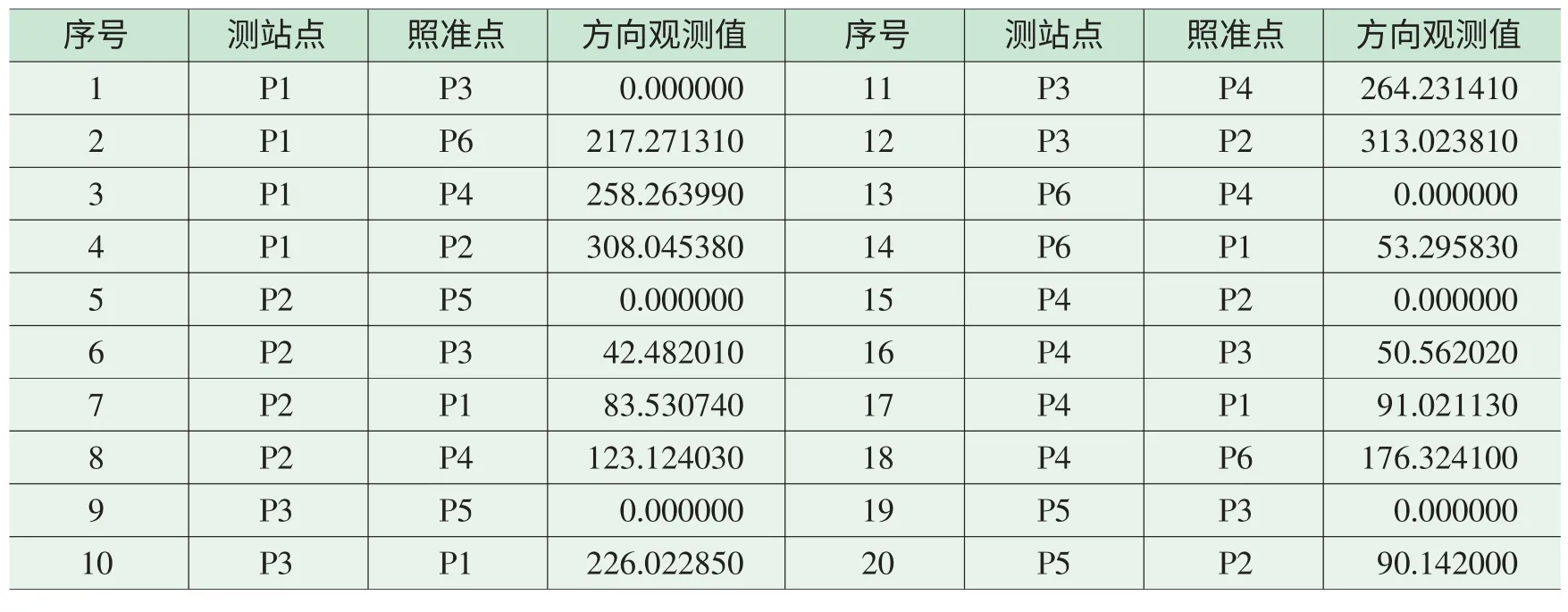
表1 方向观测值（度.分秒）

表2 边长观测值（米）

3.结果与讨论

设方向观测值的中误差为σn，边长观测值的中误差为σsj。对于任意的（秒）σ0>0，方向观测值的权为：

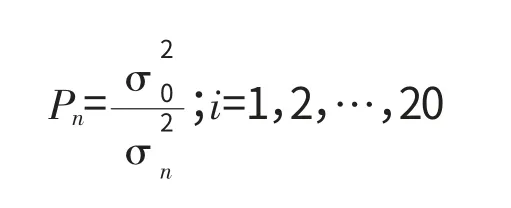
边长观测值的权为：

本例是方向观测值和边长观测值也即两类观测值的平差问题，涉及到两类观测值权的配比。通常认为方向（或角度）观测值等权，即 σn=σ0，Pn=1.0（无单位）。各边长观测值的权则按固定误差和比例误差分别计算，Psj的单位是秒2/毫米2。对于不同的σ0，通过最小二乘法可得到未知数的平差值（表3）、方向观测值的改正数和平差值（表4）、边长观测值的改正数和平差值（表5）、未知数及其函数的精度（表6）。

由表3、表4、表5和表6可知，不同的验前中误差得到的未知数的平差值、方向观测值的改正数及其平差值、边长观测值的改正数及其平差值、未知数及其函数的精度是不同的。对于验前中误差为1.00、1.80和2.02的情形，坐标未知数平差值最大互差的绝对值是 6.1毫米（表3）；方向观测值的改正数最大互差的绝对值是0.7秒（表4）；边长观测值的改正数最大互差的绝对值是7.0毫米（表5）；最弱点（P6）的点位中误差分别为13.9毫米、10.4毫米和9.7毫米，最大互差为 4.2毫米（表6）；最弱边（P4-P6）的边长相对中误差分别为 1/139000、1/213000和1/233000，相互间具有显著的差异。

当验前中误差为1.0时，验后中误差为1.87；当验前中误差为1.80时，验后中误差为2.00；当验前中误差为2.02时，验后中误差为2.02，计算结果说明可以使验后中误差与验前中误差取相同的值。

表3 边角网坐标平差值(米)

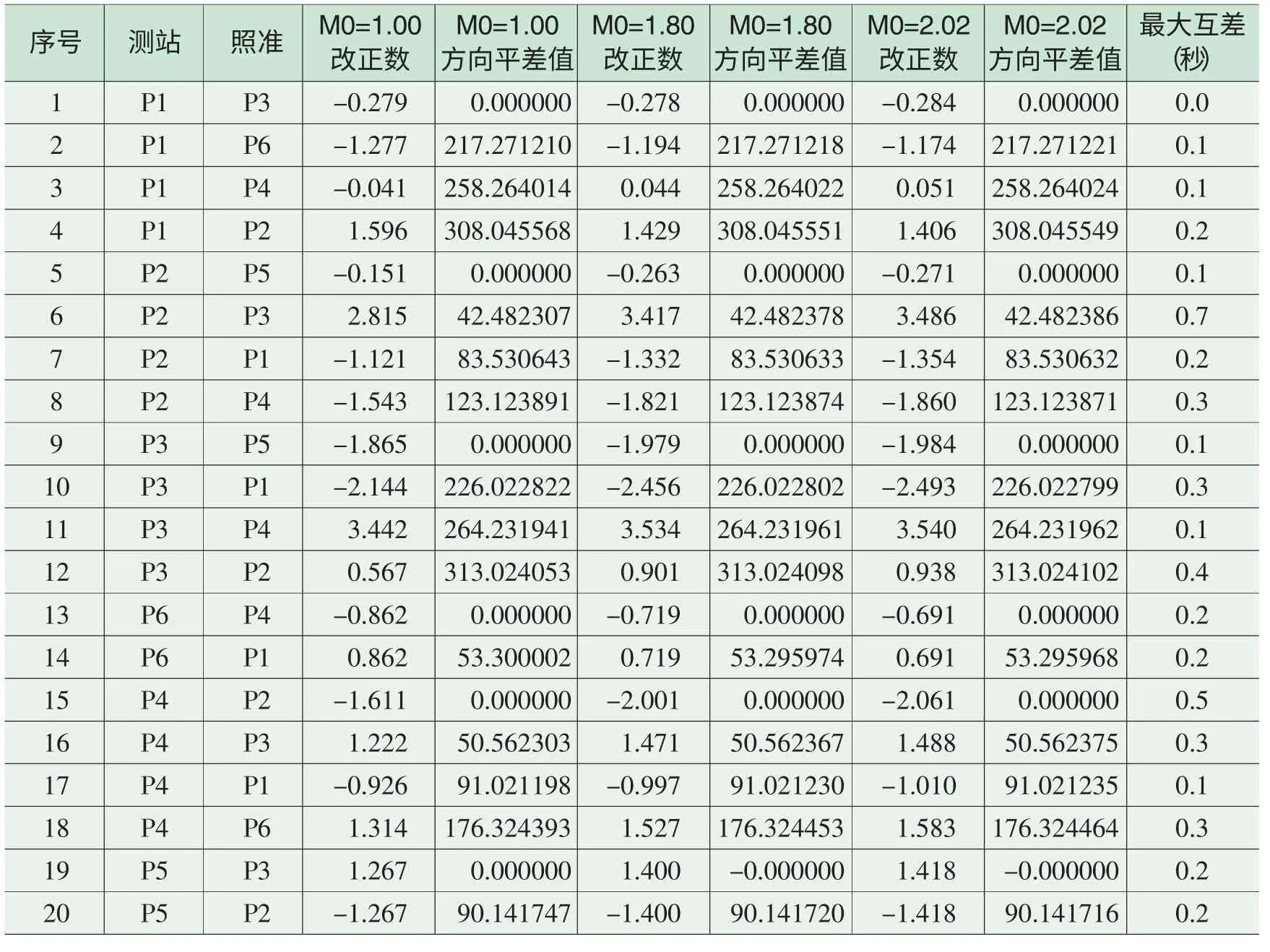
表4 边角网方向改正数（秒）和平差值（度.分秒）

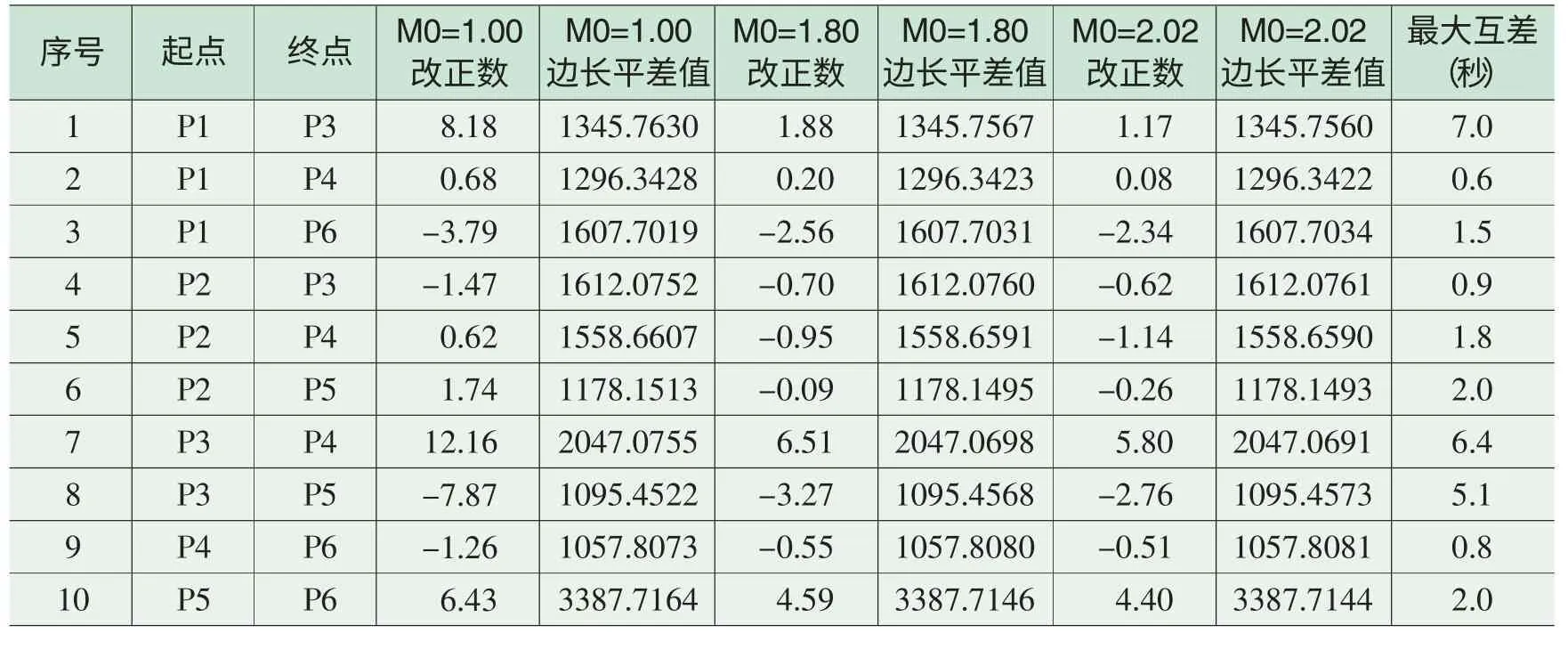
表5 边角网边长改正数（毫米）和平差值（米）

4.结论

对于两类观测值的测量控制网平差，不同的验前中误差对应着不同的验后中误差。不同的验前中误差对观测值的平差值影响并不显著，但是对平差值的精度有着较大的差异。当验前中误差与验后中误差接近时，平差结果是比较合理的。

为了得到两类及其以上观测值条件下坐标未知数、观测值改正数及其平差值和未知数及其函数的精度的唯一解，可用方差分量估计（例如Helmert方差分量估计）的方法确定各类观测值的中误差。然而在生产实践中，观测值的数量往往不能满足方差分量估计计算的需要。合理且可行的方法是通过迭代使验后中误差与验前中误差相等，通常迭代两次就能实现。

【1】高金辉.导线网平差方法的研究[J].矿山测量，1992（4）：3-5，57，61.

【2】沙月进，胡伍生，张凤梅.等价定权法原理及其应用[J].测绘通报，2004（7）:14-15.

【3】刘长建，吴洪举，黄勇.一种调整两类观测值权比的新方案[J].测绘通报，2006（9）:47-48，68.

【4】周秋生.边角网方差分量估计中定向角的处理[J].冶金测绘，1994（1）:7-13.

【5】鲍峰.带权约束参数平差法及其应用[J].同济大学学报（自然科学版），1995（2）:181-185.

【6】王仲锋.导线网方差分量估计的综合研究[J].武汉大学学报（信息科学版），2001（2）:112-117.

【7】杜永昌.导线网相关平差[J].勘察科学技术，1984（5）:48-51.

【8】马凌会.导线网坐标差观测值相关平差方法研究[J].测绘与空间地理信息，2009（3）:205-207.