取太极精髓，塑高效课堂

章薇薇

周敦颐在《太极图说》中说：“无极而太极，太极动而生阳，动极而静；静而生阴，静极复动。”太极内涵博大精深，其“天人合一”、“形神合一”、“虚实相生”、“刚柔相济”、“四两拔千斤”等特点，无不启发着教师们，如何借太极之力，提高课堂效率？如何学会“以功为本”、“借力打力”、“意动形随”使师生能在轻松快乐的氛围中，轻松获取数学知识？带着这两个疑问，笔者作了如下的探究。

一、数学练习重于变—以静制动

俗语说，不变就是变，万变不离其宗。而太极精髓就在于“以静制动”，以不变应万变。

在数学教学过程中，解题是一个必会的技能。而数学题目何其之多，让学生沉浮于题海又没有时间，如何让学生“解一题，会一类”，会触类旁通，举一反三呢？

例1：形变而质不变

原题呈现：如图1Rt△ABC，∠B=90°两直角边长分别是2，4，现将△ABC如图那样折叠，使点A与点C重合，折痕为EF，则求tan∠BAE的值？

变式1：现将△ABC如图2那样折叠，使点B落在AC边的F处，折痕为EF，则求tan∠BAE的值？

变式2：若将Rt△ABC如图3折叠，使得点B与点C重合，折痕为HG，则tan∠ABH的值是多少？sin∠BHA的值呢？

说明：本题的形一直在变化，而解决本类题的方法却没有改变，即构造直角三角形—用勾股定理（相似三角形、锐角三角函数）—列出方程，对于学生来说，题目是做不完的，教师需要通过熟悉其形，然后再了解其本质，接着对症下药，找准方向，在万变中找到其根本，进而使数学练习更扎实有效。

二、数学选例便于探—以功为本

一代太极宗师冯志强先生说：“练好太极功夫一要明理，二要会练，三要懂养。”三者缺一不可，其中“会练”是关键，“会练”就要“以功为本”。这里“功”主要就是太极内功。那么，如何打好数学课堂中的太极呢？数学课堂中的“功”指的是学生对数学题本质的理解。

例2：多解一题溯其源

如图4，在Rt△ABC中，D是边AB的中点，BE⊥CD，垂足为点E，已知AC=6，sinA= 0.8。①求线段CD的长；②求cos∠DBE的值。

对于第二小问，求cos∠DBE的值，学生用了多种思想方法。

分析：由①得，DB=5，关键在于如何求BE的长。

方法一：如图4，利用AD=DC=BD，得∠DBC=∠DCB，可用sin∠DBC=sin∠DCB，直接求出BE的长。

方法二：如图4，可证△ACB∽△BEC，直接求出BE的长度。

方法三：过点A作AMCE，构造△CMD≌△BED，得CM=BE，再用Rt△CMA，求出CM即可。

方法四：如图5，利用面积法可直接求出CM=AC、BC、AB，再证CM=EB即可。

说明：本题难度不高，在正确理解余弦的定义之后，主要难度在于如何求出线段BE的长度，学生利用锐角三角函数、相似三角形、全等三角形、面积法等均是不错的解题方法，表面上，本题解法很多，但探其本质，实则本题的关键在于如何利用自己所学的技能求出线段长，从而得出其实质内容为：求线段长度的常用方法。

三、数学讲解贵于精—四两拔千斤

太极讲究借力打力，用巧力。美国学者、著名的学习专家爱德加·戴尔1946年提出了学习金字塔理论。金字塔理论（见下表）表明：不同的教学方法，其教学效果也大不相同。若课堂上，教师口若悬河、大讲特讲、用足死力、苦口婆心，其效果却大打折扣，如何才能用最少的力达到最大的效果，教师需要向太极文化借智慧。

例3：点拨一语惊醒梦中人

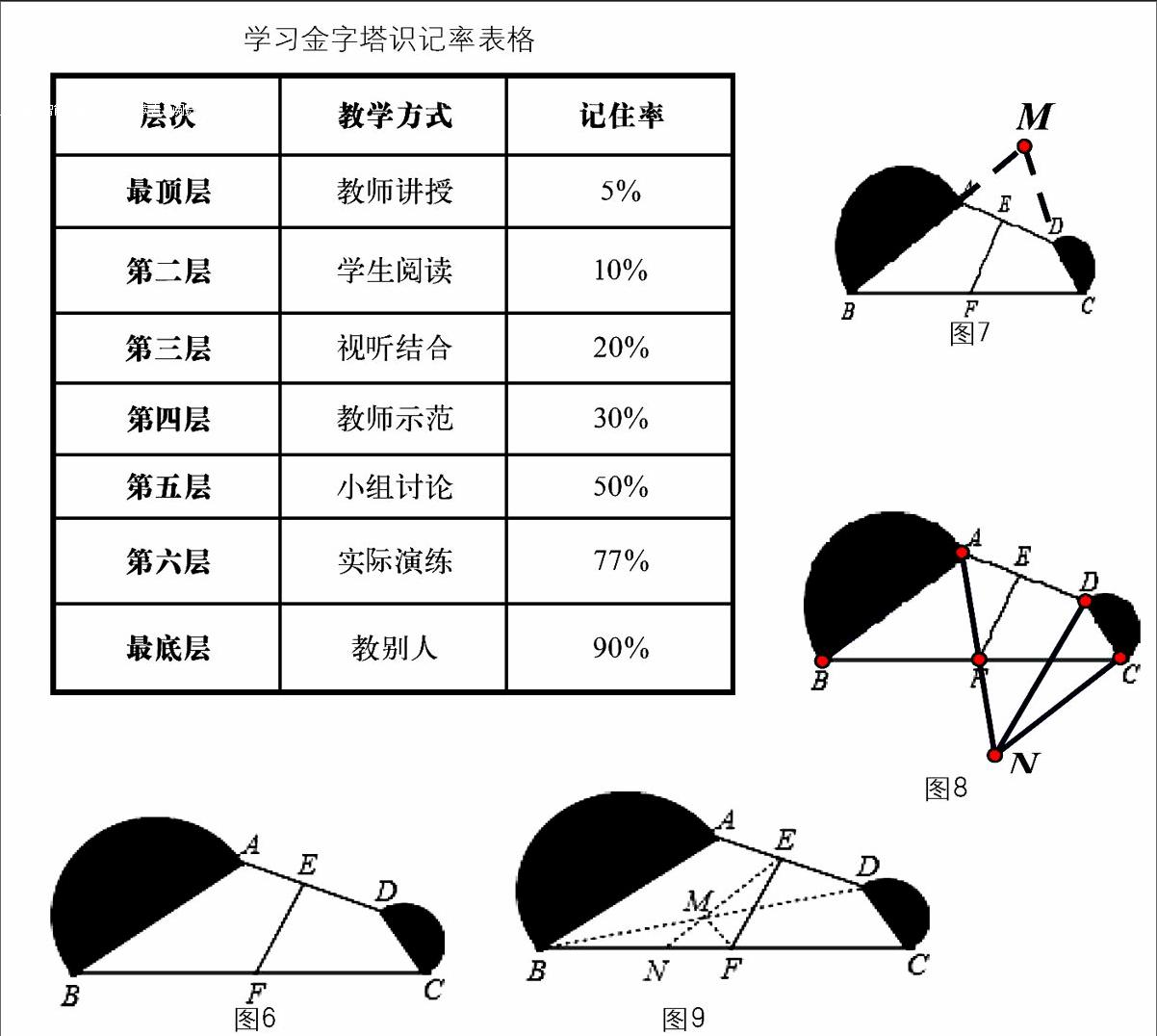
原题呈现：如图6，在四边形ABCD中，已知∠ABC+∠ACB=90°，E、F分别是AD、BC的中点，阴影部分分别是以AB、CD为直径的半圆，且这两个半圆面积之和是8π，则求EF的长度。

学生刚看到这一题时，一时不知如何下手，此时，若教师急于将辅助线交给孩子，以后再碰到类似题目，学生肯定会再次受阻，于是，此时，当孩子思维受阻时，我们教师要做的只是稍加点拔，让学生能顺藤摸到瓜。

师点拨：题中∠ABC+∠ACB=90°，让你想到什么？

学生1：延长BA，CD交于点M，则必得∠M=90°，则三角形MBC为直角三角形。（如图7）

师点拨：点E与点F为两边中点，又可以如何处理呢？

学生1：是直角三角形斜边上的中线，但不知道M、E、F是否三点共线？

学生1看着画好辅助线的图形想了会儿。

学生1：这样的辅助线没有用，即使共线也无法与阴影部分面积相联系。

师点拨：只有延长BA、CD，才能形成直角三角形？

学生2：可以通过平行线，把两个角移到一起去？过点C作CN‖AB，交AF延长线于N。（如图8）

易得∠DCN=90°，△ABF≌△NCF，EF为△AND的中位线，要得EF的长度，则只需在△DCN求出DN的长。

学生3：看到有两个中点，我想到了三角形中位线，但这两个中点无法形成中位线，我想再取一点，构成中位线。连接BD，取BD的中点M，连接EM、FM，延长EM交BC于N（如图9）。易得EM，MF是两条中位线，而∠EMF=90°则将求EF长度的问题转化为Rt△MEF的问题。

说明：当学生思维受阻，无从下手时，教师适时的引导与点拨，起的正是“四两拔千斤”之效。若教师在课堂上，能用最少的语言，达到想到的目标，让学生手动、脑想，思维活起来，那么定能让学生的知识、技能与情感得到锻炼与提升，进而使课堂更有效。

教师在借太极之力打造高效课堂的同时，更应遵循学生发展、认知规律，以培养学生能力为重，以学生的最佳发展为目的，努力做到以题为辅、以问为引、追其多法，溯其本质，努力实现师生在课堂上的最佳表现。endprint