基于高分辨率DEM数据的分形几何岩性识别方法初探
2014-11-12尹力潘蔚田青林
尹力,潘蔚,田青林
(核工业北京地质研究院,遥感信息与图像分析技术国家级重点实验室,北京100029)
岩石作为矿物的集合体具有特定的结构和构造,这种特定的结构构造会反映到宏观层面,如遥感图像上。遥感地质工作者在长期的图像解译中发现,不同类型的岩石形成的自然表面是不同的,如在图像上沉积岩线理或平行线理显得比较明显,火山岩的沟壑方向分布均匀,而花岗岩的沟壑分布有明显的方向性等。所以可以利用目视解译的方法对岩性进行识别。这种目视识别特征,如能利用数学方法进行描述,就有可能促进岩性识别的智能化发展,从而减少目视解译中的主观性和随意性。分形理论致力于研究自然物体的几何特征,并力求从几何特征表征方面的一系列参数来阐述、揭示其非线性动力学机理。许多物理现象的时间或空间函数关系的图形都呈现出分形特征,因而在材料、地质、无线电、金融、社会生活等方面分形理论都有着广泛的研究与应用。遥感研究的地物自然地表表面纹理复杂,难以用一般统计学的参数描述,自1975年B.B.Mandelbrot创立分形几何学理论以来,分形理论被广泛用于山脉、河流等地表真实景观的模拟[1-2],Pentland提出用分形维数去描述自然表面的粗糙度[3],遥感地质中利用分形研究地表纹理特征,多数研究采用计算图像的分形维度作为一个特征参数进行图像分类,识别地物提高分类效果[3-7]。然而维度对复杂图像刻画的精度还不够,自动分类的精度难以满足实际要求,因此,近年来利用多重分形谱对图像进行研究成为新方向[8-9]。本文尝试对航空LIDAR数据生成的DEM数据进行多重分形谱计算来实现岩性分类。
1 多重分形与多重分形谱
简单的分形用一个分形维数就可以描述它的特征。但是对于包含多个或多层次简单分形的复杂现象,只用一个分形维度已不能完全描述其特征,需要对每个或每层的分形特征进行刻画,这种用多个参量才能描述的分形就是多重分形[10]。
为了描述这样的复杂的不均匀性,我们把研究对象 (取其线度为1)分成N等份,每一等份的 “盒子”线度为ε,ε是一个远远小于研究对象线度的测量单位,定义第i个盒子的密度分布函数为Pi。
对于完全均匀的分布,显然有Pi(ε)~εd,d是研究对象所占据的拓扑维数。对于一个简单的分形体,有Pi(ε)~εD,D是研究对象所占据的分形维度。而对于复杂的分形分布,Pi(ε)~εα。非整数α一般称为奇异指数,也称为霍德尔 (Hóelder)指数。D可以看成是在特定情况下,α取值范围缩小到一个点的特例。α取具有相同α值的小盒子的数目记为Nα(ε),它与ε的大小有关,并可以写成

与简单分形中的N(ε)~ε-D相比 (N(ε)为被占据的 “盒子”的数目),不难看出地f(α)的物理意义是表示具有相同α值的子集的分形维数。一个复杂的分形体就可以描述成一系列不同α值所表示的子集,这样多重分形谱α-f(α)谱就能给出这一系列子集的分形特征。
2 实验样本和实验方法
2.1 实验样本
实验区位于东天山东端的甘肃方山口地区,选取5种岩性,每种岩性取3个样本进行研究。样本主要特征见表1,样本DEM数据见表2。
实验所用高分辨率DEM数据是遥感重点实验室航空激光雷达获取的激光点云数据生成的DEM图像,其空间分辨率为1m,水平误差0.4m,高程误差是0.1m。

表1 实验区5类岩石和沉积物样本岩性及纹理特征Table 1 The main texture feature of the five class rocks and sediments in the study

表2 样品DEM三维显示效果Table 2 3Dsurface of the five class sample in the study

续表2黑云母花岗岩第四纪沉积物混合岩硬砂岩图例 0 100200m
2.2 实验方法
归一化DEM数据,归一化的最大值取15个样本的最大值,最小值分别取15个样本的最小值。计算归一化后样本的盒计维度 (表3)。
采用FRACLAB软件计算归一化后各样本数据的多重分形谱[11]。经抽样对比计算,精度参数设定为0.19,维度计算方法采用盒计维度算法,即计算有相同奇异指数α的盒计维度作为多重分形谱的纵坐标,区域的灰度统计方法 (Capacity)选择sum,即把某个区域灰度值的和作为维度计算的依据,其他参数选取默认参数,其详细计算方法参见FRACLAB帮助文件。计算结果如图1所示。
3 编号结果分析
从图1可以看出,不同类岩石DEM数据的盒计维度有差异,盒计维度值与其表面的复杂程度成正比关系。这表明单纯的盒计维度是一个相对简单的参数,能表示一幅图像的复杂程度,但是不能刻画纹理在不同尺度的独特特征。DEM的盒计维度值能作为区分不同类别岩石的一个参数,但不同类型图像盒计维度值差别微小,区分度不高,不能作为精确识别岩性的依据,需要更为精确的参数来描述图像不同尺度的纹理特征。
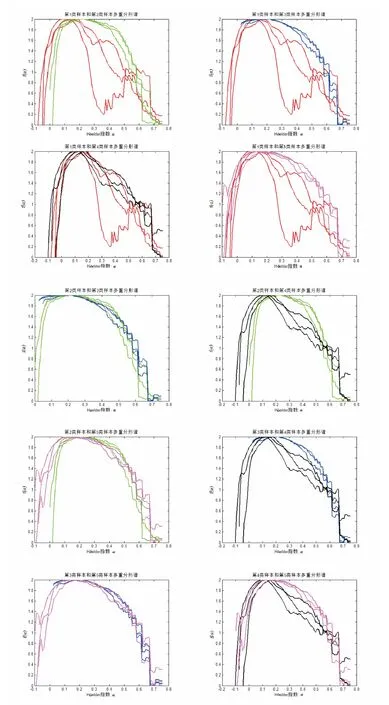
图1 样品DEM多重分形计算结果Fig.1 Multifractal spectra of the DEM of the five classes samples in the study
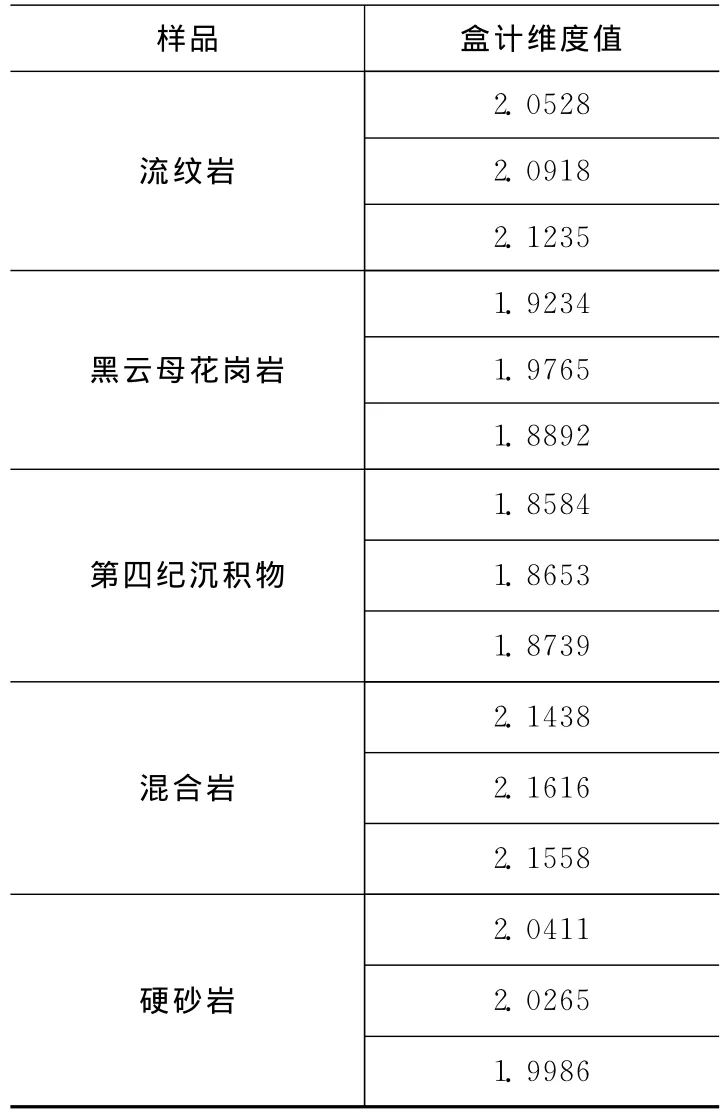
表3 样品盒计维度计算结果Table 3 Box dimensions of the five classes samples in the study
多重分形的结果表明,第3类样本的多重分形曲线特征与其它类别特征差异最明显,由于样本高程起伏很小,几乎是平面,所以在表征强烈变化的细纹理部分 (即α小于0的部分)的曲线没有值,这与目视感官结果一致。第1类样本图像的细纹理发育比较强烈,所以当α在-0.1~0之间时多重分形谱线比较完整。第1类样本在粗纹理和细纹理间连续性不好,跨度比较大,当α在0.2~0.6之间时谱线值比较低。第2类样本由于高差比较小,细纹理发育不强烈,所以当α小于0时多重分形谱值相对较低。有一样本由于表面接近于第3类样本,所以曲线也就接近于此类样本,但由于花岗岩特殊的力学性质,中尺度纹理发育强烈,当α为0.2~0.4时纹理发育强。当α在0.5附近时谱线值迅速下降,当α在0.55附近时谱线值显著低于和花岗岩一样发育有中尺度纹理强的岩石类型。第4类样本由于是古老的变质岩,大沟状纹理发育强烈,所以当α在0.6附近时,其多重分形谱的值要大于其它各类,也表明这一类岩石比较容易形成大的沟系。第5类样本和第1类样本的曲线有相似之处,细纹理发育比较强烈,粗纹理也有发育,在中尺度纹理发育要明显弱于其它类型。第5类和第1类样本曲线相比,α在0.5附近时,第5类样本值为1.1,高于第1类样本值0.9。
岩石自然表面形态主要决定于 (取决于)其内部组成。岩石自然的表面形态主要由风化形成,而地物内部的结构和物质组成决定了风化的特性。对于岩性和成分相近的岩石,其风化特征接近,所以在表面形态上有相似的特征。如果能够定量刻画其纹理特征的共性,就可以充分利用DEM具有的信息,达到遥感光谱分类所不能达到的效果。地球表面的地物形态有很强的自相似性,符合分形的特征,多重分形谱可以刻画地物不同尺度的纹理特性,揭示地物纹理的分布规律。所以多重分形谱可以用来定量刻画岩石的DEM纹理,从而对岩性进行识别。由于自然地表纹理过于复杂,盒计维度不能达到精确刻画自然地表纹理在不同尺度的分布特征,所以用多重分形谱对自然表面进行刻画的效果要优于简单的盒计维度。
4 结论
通过计算岩石DEM的多重分形谱可以得到以下结论:(1)多重分形谱可以用来定量刻画岩石DEM不同尺度的纹理特征;(2)可以利用岩石DEM多重分形谱不同部分的值来区分岩性;分形谱可以作为岩性自动分类的标准,利用分形谱的差异性进行遥感影像纹理分类和岩石信息提取;(3)室内与野外结合,野外验证是最终识别岩石类型的重要标准。
多重分形谱理论上可以用来描述岩石的表面形态,但要准确识别每一种岩性还有许多问题亟待解决: (1)岩石表面形态与内部结构、物质组成之间的关系需要探究; (2)多重分形谱计算参数的选择只能采用统一或默认值的方式解决,今后需要明确原则。
[1]杨绍国,尹忠科,罗炳伟.分形多尺度纹理图像分割 [J].模式识别与人工智能,1998,11(3):349-351.
[2]郑桂香,蔺启忠.遥感图像分形特征提取与分割[J].遥感信息,2008,9 (7):9-15.
[3]A.P.Pentland.Fractal based description of natural scenes [J].IEEE Transactions on Pattern Recognition and Machine Intelligence,1984,6(6):661-674.
[4]舒 宁.卫星遥感影像纹理分析与分形分维方法[J].武汉测绘科技大学学报,1998,23 (4):370-373.
[5]薛重生,王 霞.基于分形几何的遥感图像纹理分析方法及应用 [J].地质科技情报,1997,16(增刊):99-105.
[6]Sonny Novianto,et al.Near optimum estimation of local fractal dimension for image segmentation[J].Pattern Recognition Letters,2003,24(1):365-374.
[7]李 平,胡可乐,张秉宏.多重分形在材料分析中的应用 [J].南京航空航天大学学报,2004,26 (1):78-81.
[8]韩书霞,戚大伟,于 雷.基于多重分形的原木CT腐蚀图像的处理与分析 [J].森林工程,2007,23 (5):15-18.
[9]潘 蔚,倪国强,李瀚波.基于遥感图像地形结构-岩性组分分解的岩类多重分形特征研究[J].地学前沿,2009,16 (6):248-256.
[10]陈 颙,等.分形几何学 (第2版) [M].北京:地震出版社,2011.
[11]Lévy Véhel J,Legrand P.Signal and image processing with FRACLAB [M].Novak M M.Thinking in Patterns,Fractals and Related Phenomena in Nature.Singapore,London,New Jersey,Hong Kong:World Scientific Publishing Co.,2004.
