一维无限深势阱的波函数
2014-11-10贾晶
贾 晶
(山西大学物理电子工程学院,山西太原 030000)
一维无限深方势阱中束缚态作为量子力学最基本的问题,大部分的量子力学书中都有讲述[1~2].由于它是可以求得解析解的为数不多的例子之一,所以研究它的状态对于掌握量子力学的基本概念和处理问题的方法都有帮助,所以近年来仍然有不少文章对它进行讨论,并提出一些新的见解[3~6].
本文讨论一维无限深方势阱中束缚态中波函数的相位问题,其中数学计算相对容易,物理图像清晰,对于深入理解波函数具有相位不确定性这一特性可以起到一定的积极作用.
1 无限深势阱的波函数
考虑在一维空间中运动的粒子,它的势能在一定区域内(x=-a到x=a)为零,而在此区域外势能为无限大.粒子的势可由下式描述:

这种势称为一维无限深势阱.它的一组波函数的解为:

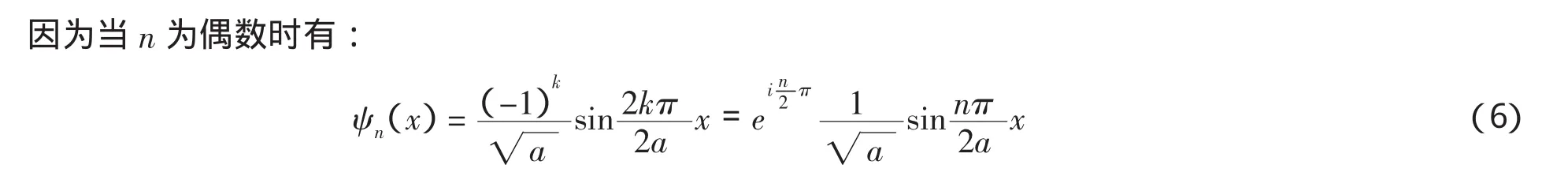
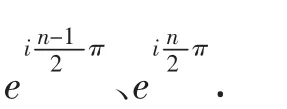
2 波函数曲线
由(2)和(3)式可作出波函数图1~图6.由(4)式作出的波函数图为图7~图12.作图时以势阱宽度a为单位长度.下面根据(2)式编制程序绘制n=2,4,6的波函数,根据(3)式编制程序绘制n=1,3,5的波函数.而根据(4)编制的程序可以绘制n=1,2,3,4,5,6的波函数.
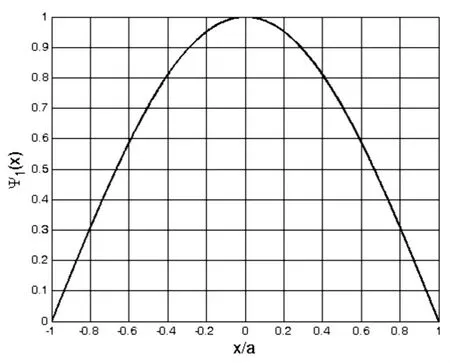
图1 利用式(3)绘制的n=1的波函数图像
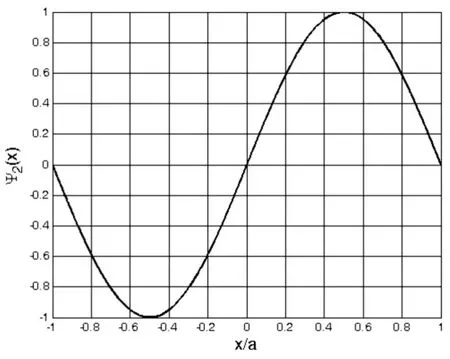
图2 利用式(2)式绘制的n=2的波函数图像

图3 利用(3)式绘制的n=3的波函数曲线

图4 利用(2)式绘制的n=4的波函数曲线

图5 利用(3)式绘制的n=5的波函数曲线

图6 利用(2)式绘制的n=6的波函数曲线
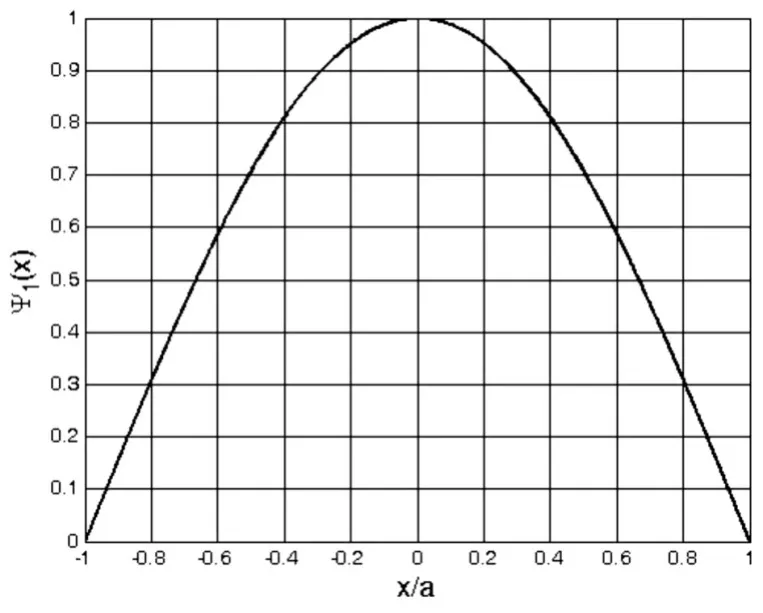
图7 利用式(4)绘制的n=1的波函数图像

图8 利用式(4)绘制的n=2的波函数图像

图9 利用(4)式绘制的n=3的波函数曲线

图10 利用(4)式绘制的n=4的波函数曲线

图11 利用(4)式绘制的n=5的波函数曲线

图12 利用(4)式绘制的n=6的波函数曲线
从(5)和(6)式看出(2)式、(3)式与(4)式之间有一个相位差为(-1)k=eikπ=einπ/2(k=n/2)(n偶数)和(-1)k=eikπ=ei(n-1)π/2(k=(n-1)/2)(n为奇数).所以当n=1,4,5…时两者绘出的波函数图形是相同的,但当n=2,3,6,7…时两者绘出的图是反相的.即当n取奇数时,对于使ei(n-1)π/2=1的奇数两波函数的相位相同,对于使ei(n-1)π/2=-1的奇数两波函数的相位相反.即当n取偶数时,对于使einπ/2=1的偶数两波函数的相位相同,对于使e-inπ/2=-1的偶数两波函数的相位相反.
3 概率密度曲线
当然(2)和(3)式与(4)式描写的粒子的概率密度应该是一致的,这非常关键,因为在同一时刻同一地点找到粒子的概率是一可测量的物理量,解应该是唯一的,不可能存在两种不同的结论.根据量子力学的基本原理,波函数可以相差一常数相位因子,所以(2)式和(3)式与(4)式描写的波函数都是可以的(仅差一相位因子).我们分别由(2)和(3)式与(4)式绘制的概率密度曲线,如图13~图18.发现由(2)和(3)式与(4)式绘制的概率密度曲线完全一致.

图13 n=1对应的概率密度曲线

图14 n=2对应的概率密度曲线

图15 n=3对应的概率密度曲线

图16 n=4对应的概率密度曲线

图17 n=5对应的概率密度曲线

图18 n=6对应的概率密度曲线
此问题也可利用有限差分法进行数值计算.结果见图19~图24.对比发现与(2)和(3)式或(4)式描写的波函数均不完全一致,似乎有一定的“随意性”.量子力学中的波函数的可以相差一相位因子是这种“随意性”存在的依据.当然由此得到的概率密度分布与解析解得到的概率密度分布曲线是完全相同的.

图19 数值计算得到n=1的波函数

图20 数值计算得到n=2的波函数

图21 数值计算得到n=3的波函数

图22 数值计算得到n=4的波函数
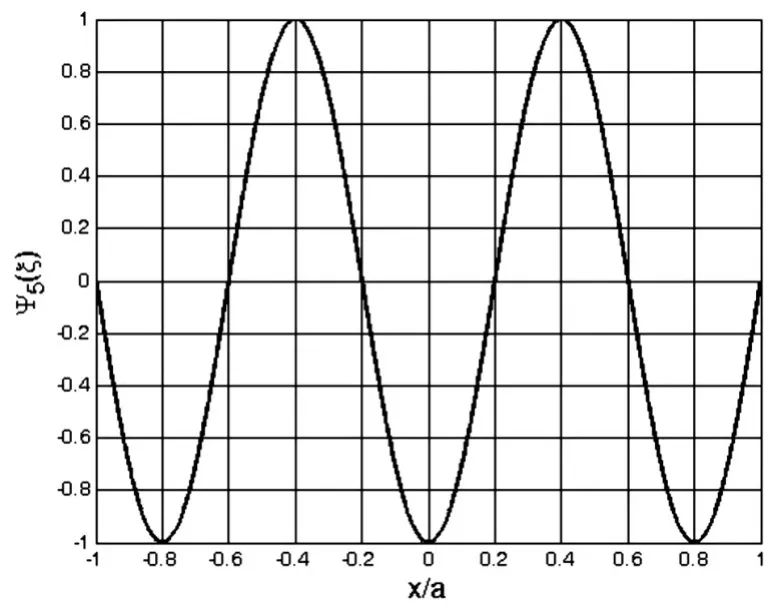
图23 数值计算得到n=5的波函数

图24 数值计算得到n=6的波函数
4 总结
量子力学的基本原理告诉我们,归一化后的波函数仍然存在一不确定的常数相位因子,因此波函数的图像可能不完全相同,但由于粒子分布的概率密度是一个量子力学中的可测量的量,所以应该是唯一的.
我们在本文中分析了无限深势阱的不同解析解对应的波函数及数值解对应的波函数,分析了它们存在不同的原因及这种不同的合理性.同时也指出它们所对应的概率密度分布是完全一致的,这也是量子力学所要求的.
[1]周世勋.量子力学教程[M].北京:高等教育出版社,1979.
[2]曾谨言.量子力学[M].3版.北京:科学出版社,1981.
[3]额尔敦朝鲁.关于一维无限深方势阱描述的一个注记[J].大学物理,1997(11):50.
[4]郑富年,聂义友.一维无限深方势阱中运动粒子的讨论[J].景德镇高专学报,1996(4):5~8.
[5]王国文.一维无限深势阱中粒子动量概率分布引出的问题[J].光子学报,1998(5):6~7.
[6]易其顺.一维无限深势阱内粒子概率密度演示仪[J].物理实验,2010,30(7):24~26.
