基于用户相似度迁移的协同过滤推荐算法*

柯良文，王 靖

（华侨大学 计算机科学与技术学院，福建 厦门361021）

协同过滤技术是推荐系统中应用最为广泛和成功的推荐技术之一[1]，其基本思想是：利用整个用户集对项目集的历史评分数据来预测目标用户对其未评分的项目集的偏好程度，从而选择若干个预测后偏好程度最高的项目作为推荐结果[2]。

传统的协同过滤算法最为关键的步骤是度量用户之间或项目之间的相似度。随着系统规模的不断扩大，用户对项目评分数据极端稀疏时，利用传统的方法难以准确地度量相似性，导致了推荐系统的推荐质量降低。为了缓解稀疏性的问题，多领域数据的迁移学习已受到了学者们的高度关注。目前，研究者已提出了多种基于迁移学习的推荐算法，如SINGH等人提出了一种联合矩阵分解模型 CMF(Collective Matrix Factorization)[3]，Li Bin等人提出了一种评分矩阵生成模型RMGM(Rating Matrix Generative Model)[4]，Pan Weike等人则提出了一种坐标系统迁移模型CST(Coordinate System Transfer)[5]。这些算法均通过对辅助领域的知识进行迁移来帮助提高目标领域的推荐精度。

然而，在现有的迁移学习推荐算法中，如CMF模型和CST模型，需要辅助领域与目标领域的用户空间一致，并且模型中需要控制较多的参数，受到了一定的限制。针对这些局限，本文提出一种用户相似度迁移的协同过滤模型 UST(User Similarity Transfer)，对辅助领域和目标领域共同用户的相似度进行迁移。为了能够充分利用辅助领域的用户评分信息，本文的模型在辅助领域里采用先填充后计算用户相似度的策略。另一方面，通过一种用户特征子空间的距离来度量模型中的平衡参数，一定程度上消除了人为调控的局限性。

1 相关定义

首先给出本文中所使用的符号及含义。在辅助领域里，定义一个p×q的矩阵RA来表示p个用户对q个项目的评分；在目标领域里，定义一个m×n的评分矩阵RT来表示m个用户对n个项目的评分。评分矩阵的项ri，j表示用户ui对项目vj的偏好程度，分值越大表示用户对项目的偏好程度越高。为了方便描述评分矩阵的项是否被评分，在辅助领域和目标领域里分别定义一个只有0和 1值的标记矩阵 WA和WT，其中0表示该项未被评分，1表示该项已被评分。

2 基于用户的协同过滤算法

基于用户的协同过滤算法根据其他用户的观点产生目标用户的推荐列表。首先利用已有的评分数据计算目标用户与其他用户的相似度，其次通过目标用户的最近邻居对某个项目的评分来预测目标用户对该项目的评分[6]。

2.1 相似度的计算方法

相似度的计算是基于用户的协同过滤算法中最为关键的一步。传统的相似度度量方法有余弦相似度、修正的余弦相似度和pearson相关系数[2]，本文采用实践中实现效果较好的pearson相关系数来度量[7]。设I是ui和uj共同评分的项目集合，则 ui和uj的pearson相似度计算方法如下：

其中，ri、rj分别表示ui、uj对它们共同评分项目的平均评分。

2.2 产生推荐结果

根据目标用户ui的最近邻居集合C对项目的评分信息预测ui对未评分项目的评分，选择预测评分最高的若干个项目作为推荐结果反馈给目标用户。目标用户ui对未评分项目vk的预测评分，可以根据ui的最近邻居集合C对vk评分的平均加权得到[8]，计算方法如下：

其中，ri、rj分别表示用户 ui、uj对其已知评分项目的平均评分。

3 基于用户相似度迁移的推荐模型

3.1 UST模型介绍

现实世界中，辅助领域和目标领域往往只有部分共同的用户或项目，导致大部分现有的迁移学习算法在实际应用中具有一定的局限性。为了能够提高传统协同过滤算法用户相似度计算的准确性，本文从相似度迁移的角度出发，建立用户相似度迁移模型，以更好地利用辅助领域的评分信息帮助目标领域用户相似度的学习。

定义Asim为辅助领域计算得到的用户相似度矩阵，Tsim为目标领域计算得到的用户相似度矩阵，通过加权的方法建立如下UST模型：

其中，α为平衡参数，用来控制辅助领域的用户相似度对目标领域用户相似度学习的迁移程度。

在UST模型中，首先利用辅助领域用户评分数据计算用户之间的相似度，然后通过式(3)计算目标领域的用户相似度矩阵，最后对目标领域未评分的项目进行预测。

3.2 辅助领域用户相似度的学习

为了利用辅助领域的评分数据来计算用户相似度矩阵，UST模型首先通过一种填充的方法对辅助领域的缺失评分矩阵进行填充，然后对填充后的矩阵计算用户间的相似度。这样做的好处是能够更有效地利用辅助领域已知评分的信息来计算用户的相似性度。

矩阵分解MF(Matrix Factorization)技术是一种有效的填充方式，它希望通过找到一个低秩的矩阵来逼近RA[9]。记填充后的低秩矩阵为ZA，则通过矩阵分解的方法可以将ZA近似分解成如下形式：

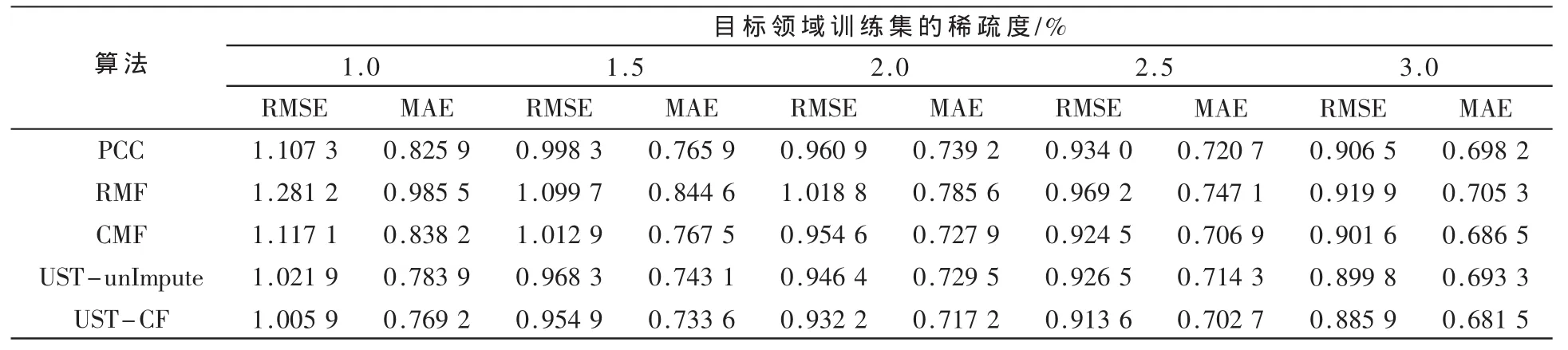
其中，d 表示特征的维度，d<

其中，||·||F表示 Frobenius范数，⊙表示 Hadamard积，例如(W⊙R)i，j=Wi，jRi，j。 为 了 避 免 过 度 拟 合 ， 在 式 (5)中 引入了正则项，则矩阵分解的模型可以修改为：

其中，λ1、λ2为正则项的控制参数，用来协调实际用户评分矩阵和矩阵分解模型学习后的填充矩阵之间的训练误差。为了获得式(6)模型的最优解，参考文献[10]提出了一种交替最小二乘ALS(Alternation Least Squares)的迭代算法，它通过求 ∂Γ(U，V)/∂U=0 和 ∂Γ(U，V)/∂V=0 来交替地更新U和V，使模型逼近最小值，具体计算公式如下：

进一步地，将辅助领域填充后的矩阵ZA通过式(1)计算出辅助领域的用户相似度矩阵Asim。

3.3 目标领域用户相似度的学习

在UST模型中，α的大小受到目标领域和辅助领域相关性的影响。为了度量α的值，采用一种目标领域和辅助领域的用户特征子空间距离来估计。设正交矩阵UT和UA分别是目标领域和辅助领域的用户特征矩阵，则UT和UA的子空间距离可由下式计算：

其中，σ min(Z)表示Z的最小奇异值。为了获得辅助领域和目标领域的用户特征子空间UT和UA，可以通过矩阵的QR分解将U分解成一个列正交的矩阵Q和上三角矩阵 T[11]：

确定了平衡参数α，根据模型式(3)计算出目标领域最终的用户相似度矩阵，最后通过式(2)为目标用户产生推荐结果。

4 实验结果和分析

为了验证UST-CF算法的有效性，选取了以下几种经典的非迁移学习协同过滤算法和迁移学习的协同过滤算法做比较：基于pearson相关相似性的协同过滤算法(PCC)[6]；基于传统矩阵分解的单个目标领域协同过滤算法(RMF)[10]，即本文式(6)的模型；联合矩阵分解的协同过滤算法(CMF)。为了验证辅助领域评分矩阵填充后是否有利于提高目标领域用户相似度计算的准确性，本文还对辅助领域未填充的UST-unImpute算法进行比较。

4.1 实验数据集

采用 MovieLens(http://www.gouplens.org/node/73)站点的电影评分数据集来对比各种算法的效果。MovieLens数据集包括71 567个用户对10 681个电影项目的约107条评分数据，其评分形式为{0.5，1.0，1.5，…，5.0}。为了度量整个数据集的稀疏性，引入数据稀疏度的概念，定义为用户已评分数据占整个数据集的比例，可以得到该数据集的稀疏度为 107/(71 567×10 681)≈1.31%。

4.2 评价标准

推荐系统的质量由预测结果的精度决定。实验中，采用两种广泛的评价方法：均方根误差RMSE(Root Mean Square Error)和平均绝对误差 MAE(Mean Absolute Error)，具体计算方式如下：

其 中 ，pi，j、ri，j分 别 表 示 预 测 评 分 值 和 实 际 评 分 值 ，TE表示训练集的下标集合。

4.3 参数设定

对几种比较算法的参数做如下设定：对于基于最近邻的协同过滤算法(如 PCC、UST-unImpute、UST-CF)，选择的最近邻居数为{5～300}；对于RMF模型和CMF模型，选择的特征维度为{4，5，…，10}，正则项参数为{0.1，1，5，10}，平衡参数为{0.1，0.5，0.9}。

4.4 实验方案和结果分析

根据目标和辅助领域的用户集相同且评分形式一致、用户集相同但评分形式不一致、用户集不相同但评分形式一致这三种情形设计3个实验方案，每种方案的辅助领域的稀疏度均固定为5%。

方案1用户集相同且评分形式一致

从数据集中随机选取1 000个用户对2 000个电影的评分数据，将其中1 000部电影作为辅助领域的项目，剩余的1 000部电影作为目标领域的项目。目标领域内每个用户至少评价过25部以上的电影。进一步地划分目标领域的训练集和测试集，其中训练集按照不同的数据稀疏度划分为5组，每一组的稀疏度依次为1.0%、1.5%、2.0%、2.5%和3.0%，而每组剩余的评分数据作为测试集。

方案2用户集相同但评分形式不一致

从数据集中随机选取1 000个用户对1 500个电影的评分数据，将其中1 000部电影作为辅助领域的项目，剩余的500部电影作为目标领域的项目。在辅助领域里人为地对用户评分数据进行如下转化：对评分≧4的项用1来代替，评分<4的项用0来代替。目标领域里每个用户至少评价过20部以上的电影，训练集和测试集的划分同方案1。

方案3用户集不同但评分形式一致

从数据集中随机选取2 000部电影，其中1 000部作为辅助领域的项目，剩下的1 000部作为目标领域的项目。辅助领域和目标领域的用户数均固定为1 500个，并且按照两个领域的共同用户数划分5组实验。每组实验的共同用户数分别为 300、600、900、1 200、1 500。 目标领域里每个用户至少评价25部以上电影，并且训练集的稀疏度为1%。

三个实验方案的结果分别如表1～表3所示。从实验结果可以看出，与其他协同过滤算法相比较，本文提出的UST-CF算法均能取得最好的推荐效果。从表1和表2可以看出，目标领域的稀疏度越低，UST-CF算法取得的优势越明显，这说明对评分数据极其稀疏的情形，UST-CF算法体现了更好的适应性,能有效缓解数据稀疏的问题。从表3可以看出，即使只有部分的共同用户，UST-CF算法也能有效利用这部分共同用户的评分数据，改进目标领域测试集的推荐精度。

本文提出了一种用户相似度迁移的协同过滤推荐算法，有效地缓解了目标领域数据稀疏性的问题。此外，算法采用一种用户特征子空间的距离来度量UST模型中的平衡参数，大大提高了模型的智能性。本文算法只考虑了对辅助领域的用户相似度进行迁移，因此如何改进模型，使模型能够对辅助领域的其他知识进行迁移(如用户的评价特征、项目的属性等)，进一步提高目标领域的推荐精度，是一个有意义的研究方向。

表1 方案1实验结果比较

表2 方案2实验结果比较

表3 方案3实验结果比较

[1]SU X，KHOSHGOFTAAR T M.A survey of collaborative filtering techniques[J].Advances in Artificial Intelligence，2009(4)：1-19.

[2]马宏伟，张光卫，李鹏.协同过滤推荐算法综述[J].小型微型计算机系统，2009，30(7)：1282-1288.

[3]SINGH A P，GORDON G J.Relational learning via collective matrix factorization[C].Proceeding of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，ACM，2008：650-658.

[4]Li Bin，Yang Qiang，Xue Xiangyang.Transfer learning for collaborative filtering via a rating-matrix generative model[C].Proceeding of the 26th Annual Internatioal Conference on Machine Learning，ACM，2009：617-624.

[5]Pan Weike，XIANG E W，LIU N N，et al.Transfer Learning in Collaborative Filtering for Sparsity Reduction[C].AAAI，2010(10)：230-235.

[6]BREESE J S，HECKERMAN D，KADIE C.Empirical analysis of predictive algorithms for collaborative filtering[C].Proceeding of the 14th Conference on Uncertainty in Artificial Intelligence，Morgan Kaufmann Publishers Inc.，1998：43-52.

[7]MCLAUGHLIN M R，HERLOCKER J L.A collaborative filtering algorithm and evaluation metric that accurately model the user experience[C].Proceeding of the 27th Annual International ACM SIGIR Conference on Research and development in Information Retrieval，ACM，2004：329-336.

[8]SARWAR B，KARYPIS G，KONSTAN J，et al.Item-based collaborative filtering recommendation algorithms[C].Proceeding of the 10th International Conference on World Wide Web，ACM，2001：285-295.

[9]BUCHANAN A M，FITZGIBBON A W.Damped newton algorithms for matrix factorization with missing data[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition，CVPR 2005，2005(2)：316-322.

[10]李改，李磊.基于矩阵分解的协同过滤算法[J].计算机工程与应用，2011，47(30)：4-7.