深度神经网络的快速学习算法
2014-11-08卓维,张磊
卓 维,张 磊
(中山大学数学与计算科学学院,广州 510275)
0 前言
神经网络[1]是机器学习的重要分支,是智能计算的一个主流研究方向,长期受到众多科学家的关注和研究.它植根于很多学科,结合了数学、统计学、物理学、计算机科学和工程学.已经发现,它能够解决一些传统意义上很难解决的问题,也为一些问题的解决提供了全新的想法.
在传统的研究成果中,有很多表达数据的统计模型,但大都是比较简单或浅层的模型,在复杂数据的学习上通常不能获得好的学习效果.深度神经网络采用的则是一种深度、复杂的结构,具有更加强大的学习能力.目前深度神经网络已经在图像识别、语音识别等应用上取得了显著的成功.这使得这项技术受到了学术界和工业界的广泛重视,正在为机器学习领域带来一个全新的研究浪潮.
1 多层感知器的原理和相关研究
1.1 神经元
神经元[1]是受生物神经元启发而得到的计算模型.它接收到一些输入(类比于突触),然后与对应的权值相乘(对应于信号的强度)并求和,然后由一个数学函数来决定神经元的输出状态.作为计算模型,它按表达式 t=f(∑wixi+b)产生输出,在式中,输入为xi到xn,对应权值分别为wi到wn,偏置值是 b,将这些值对应相乘后送入累加器(SUM),累加器的输出会被送入一个传输函数(或称激活函数,f),由f产生最终输出t.有三种常用的激活函数:阈值函数、线性函数和Sigmoid函数.本文中采用Sigmoid函数中的其中一种:logistic函数.具体表达式为

图1 神经元的结构
1.2 多层感知器
多层感知器[1]由三部分组成:输入层,一层或多层的隐藏层,输出层.输入信号在层与层之间前向传播,通过整个网络.这种网络被称为多层感知器(multilayer perceptrons,MLPs).图2是拥有两个隐藏层的多层感知器.
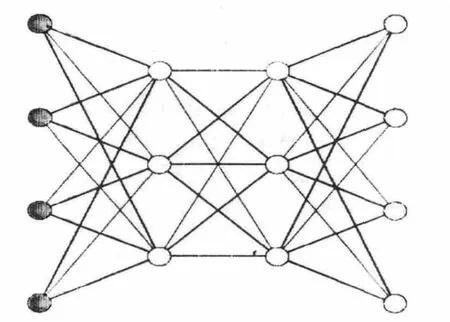
图2 含有两个隐含层的多层感知器
在图2中,每一层都含有多个神经元,同一层的每个神经元都有相同的输入神经元,即上一层的全部神经元.多层感知器中的信号从左往右逐层流过,依次根据神经元的计算方式得到各层的状态,并最终产生输出.一般地,对于多层感知器,希望对给定的输入,产生可靠的接近于目标值的输出.不同的网络权值会产生不同的处理效果,希望网络实际响应产生的输出从统计意义上接近于目标响应.通常采用反向传播算法(back-propagation algorithm)来调整网络权值,进而实现这一目的.在很多实际应用中,人们发现这种算法非常有效.通过成功的学习,可以得到输入与输出之间的复杂映射关系,比如,给定手写数字的图片,将图片的像素作为输入,可以输出图片中所包含的数字信息,即这个数字为 0,1,…,9.
1.3 反向传播算法
多层感知器中所有的权值 w1,w2,…,wn是要求的参数.假设网络的误差函数为f,极小化f将产生最优解.借助梯度下降的思想,将对这些权值依次求偏导数,传统的反向传播算法[1]将按下式更新权值,其中ŋ>0代表学习速率.上面的表达式表示每一次的学习都是沿着梯度方向下降的.
1.4 深度学习算法
在2006年前,大部分的多层神经网络都未能成功训练得到真正的最优解(除了卷积神经网络[2]),多层的神经网络一般比只含有一两个隐含层的神经网络表现更差[3].但在 2006 年后,由 Hintion[4]和Bengio[5]等人提出的深度学习算法成功地解决了深度神经网络的学习问题.这种学习方法可以理解为在采用传统的BP算法学习之前采用无监督的方法进行预训练.通过预训练,可以为后续更复杂的学习提供了较好的初始化权值,使得全部权值所构成的向量处在对全局训练有利的区域.
2 改进算法
2.1 带权值约束的神经元设计(即SCN)
在传统的神经网络中,基本的构成元素是“神经元”.在即将创建的模和固定的多层感知器中,采用的是类似的组成元素.在这里将其命名为“模和固定的神经元”(图3),为方便表达,将其简称 SCN(Sum Constant Neuron).

图3 模和固定的神经元示意图
它与传统神经元的唯一不同之处,是在权值上追加一个约束:∑=|Wi|=Ms.在输入输出响应的计算上它们都是一致的,即t=f(∑wixi+b)
2.2 基于SCN的神经网络(即SC-MLP网络)
在这种新型神经网络中,假定每个需要计算的神经元的输入权值的模的和是固定的,这个和值是一个常数,不妨就称作模和,用记号Ms表示.在这里主要讨论的是对于多层感知器的改造,对于采用SCN来代替传统神经元的多层感知器,称为模和固定的多层感知器,SC-MLP.
2.3 对SC-MLP的反向传播算法(即NBP算法)
在SC-MLP中强烈指定了模和固定这个约束条件,为此必须采用特殊的权值更新方法来学习,以保证“模和固定”.这就是我们即将提及的依神经元规范化的反向传播算法(Neuron Backpropagation,NBP).
在NBP中也将利用偏导数,只是方向与梯度不同.这个算法,可以保证模和固定.在表1中,将详述这个算法的细节.

表1 依神经元规范化的反向传播算法(即NBP算法)
3 实证分析
3.1 数据集简介
手写数字数据库(The MNIST database of handwritten digits)包含了60 000张训练图片,每张图片都是28*28像素,每张图片包含的是0~9中某个数字的手写形式(图4).这是一份经典的模式识别数据库,可以很好地用于新方法的比较和评估.很多不同的模式识别方法已经被应用于这份数据.
在这个手写数字的识别任务中,我们并不知道相关数字的几何特性,在系统建立的过程中也没有进行特殊的图像处理,在我们的实验中,仿效了文献[4]中的数据划分方法,从训练集中抽取出44 000张图片作为真实的训练集(training set),即将用作网络学习.这份真实的训练集分成440批,每批含有100个数字,数字0 ~9(图4)各含10个.在每批数字训练后进行权值更新.剩余的训练数据将用作测试集(test set),共有16 000张.

图4 手写数字示例图
神经网络的结构是784-10-10-20-10(即输入层含有784个神经元,第一、二、三个隐含层分别含有10、10、20个神经元,输出层含有10个神经元).输出层的激活函数是softmax,其他层的激活函数是,误差函数采用了交叉熵(cross-entropy).为了方便比较,设定训练次数为400(即在权值的训练过程中,训练集共使用了400次).
3.2 传统反向传播算法的学习效果
在实验中,对每一个学习率寻找合适的惩罚参数.惩罚参数是指在误差函数中添加项l‖w‖2,w是网络所有权值构成的向量,此项的加入可以有效地限制权值的大小,从而提升网络的学习能力对参数的选择,参考了文献[6]中的处理方式:按一定的数量级选择出待选的参数集,然后对这些参数进行组合实验,以确定最佳的参数组合.那么在下面的实验中,对学习率和惩罚参数,我们限定参数范围:惩罚参数学习率 ŋ∈{1,0.5,0.2,0.1,0.05},ʅ∈{10-1,10-2,10-3,10-4,10-5,10-6,0}.对于神经网络的每一层,权值都从均匀分布中随机抽样得到,其中n是上一层的神经元个数.
经过实验,可以发现学习率1和0.05分别因过大和过小而不合适.另外几个学习率对应的最佳参数组合是 {0.5,10-4}、{0.2,10-5}、{0.1,10-5},表2给出了这几个表现较优的参数组合的学习效果.

表2 传统神经网络不同学习率得到的最终模型的效果
3.3 深度学习方法的学习效果
先用自动编码机[5]的技术对除了输出层外其他层次的权值进行预训练,然后再采用反向传播算法进行训练整个神经网络.在自动编码机的训练过程中,采用了学习率为0.1,每层各训练100次.然后,用在上一节传统反向传播算法中得到的最优参数组合({0.5,10-4},{0.2,10-5},{0.1,10-5})来分别训练经自动编码机预训练的神经网络.这几个表现较优的参数组合的学习效果如表3所示,其效果明显优于采用了对应参数组合的传统模型.
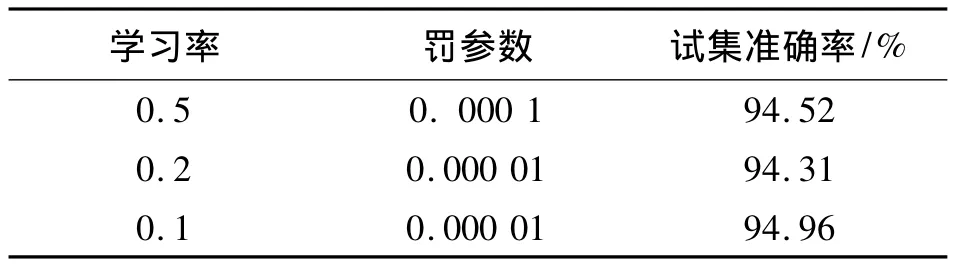
表3 深度学习得到的最终模型的效果
3.4 NBP算法的学习效果
从第一隐含层到输出层各层的模和为60、15、20、30,偏置限定值为 0.5.在模型的学习过程中,学习率采用了0.1、0.05、0.02、0.01.通过比较这四个学习率,可以发现最终在NBP算法中选择0.02的学习率是最为合适的(表4).学习率为0.02时最终达到的准确率是94.95% .
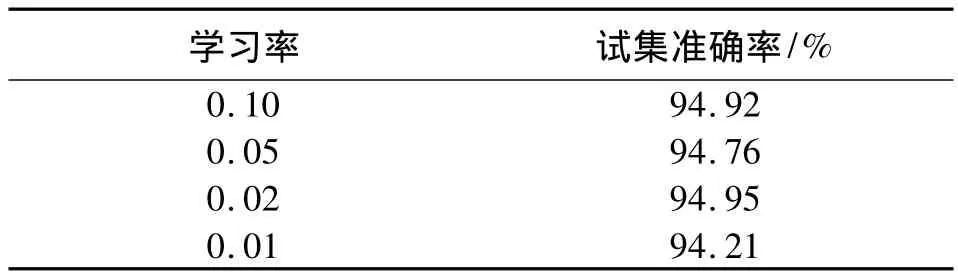
表4 NBP学习算法在不同学习率得到的最终模型的效果
3.5 各种学习算法的在手写数字识别中的结果对比
将取得最好效果的深度学习算法(即经过预训练,并且全局反向传播学习率为0.1,惩罚参数为10-5,图中标记为“auto Best”)、传统学习算法(未经过预训练,并且全局反向传播学习率为0.5,惩罚参数为10-4,图中标记为“trad Best”)及本文的NBP学习算法(学习率为0.02)进行综合的比较.在图5中,传统的反向传播算法在学习的前期就陷入了收敛,最终的学习准确率并不高.深度学习算法的准确率保持稳步的上升,最终在三种方法中获得了最高的准确率.本文中提出的NBP学习算法在精度上明显地优于传统的反向传播算法,并与深度学习算法相当.而且在学习速度上,本文的NBP学习算法很快,在上面的实验中优于深度学习算法,用较少的时间就可以达到很高的准确率.
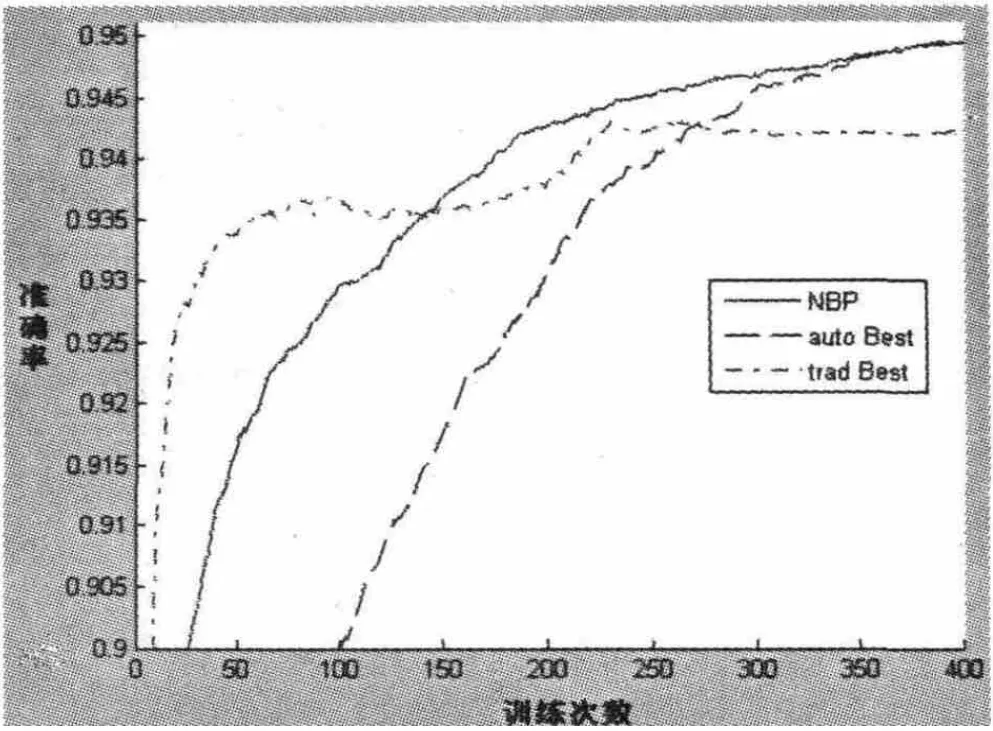
图5 NBP算法(学习率0.02)和深度学习算法(学习率0.1,惩罚参数10-5)、传统的反向传播算法(学习率 0.5,惩罚参数10-4)的对比
4 结论
随着计算机技术的发展和深度学习算法的诞生,深度神经网络的应用已经开始在现代科技中崭露头角.谷歌、微软和百度等拥有大数据的高科技公司都相继地投入大量的资源进行深度学习技术的研发.
本文提出了一个新的网络结构“模和固定的多层感知器”(SC-MLP)及与之对应的新的学习算法“依神经元规范化的反向传播算法”(NBP).在手写数字的识别问题中,本文对比分析了三种方法的效果,即:反向传播算法,深度学习算法,本文的NBP学习算法.结果表明:NBP学习算法学习很快,在实验中优于深度学习算法,可以用较少的时间达到很高的准确率,具有进一步研究的价值.
[1]HAYKIN S.神经网络原理[M].叶世伟,史忠植,译.北京:机械工业出版社,2004.
[2]SIMARD P,STEINKRAUS D,PLATT J C.Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis[C]//ICDAR.2003(3):958 -962.
[3]BENGIO Y.Learning deep architectures for AI[J].Foundations and trends?in Machine Learning,2009,2(1):1-127.
[4]HINTON G E,OSINDERO S,TEH Y W.A fast learning algorithm for deep belief nets[J].Neural computation,2006,18(7):1527-1554.
[5]BENGIO Y,LAMBLIN P,POPOVICI D,et al.Greedy layer- wise training of deep networks[J].Advances in neural information processing systems,2007(19):153.
[6]ERHAN D,BENDIO Y,COURVILLE A,et al.Why does unsupervised pre-training help deep learning?[J].The Journal of Machine Learning Research,2010(11):625-660.
