中小企业供应链金融演化博弈分析

南京工业大学 陆旦强

一、供应链金融概述

供应链金融源自于企业供应链管理，是在整个经济系统的分工由企业内分工向企业间分工的演变过程中，伴随着供应链上企业资金管理而产生的。供应链所阐述的主要是企业间的分工，即整个供应链的各个环节分别由不同的企业独立完成，不同企业之间乃至整个生产过程通过市场交易机制来协调。供应链上的独立企业有着明确的职能分工，其中的核心企业通过对“三流”，即信息流、物流及资金流的控制，从原材料的采购入库，中间环节的生产控制到最后的产品销售，将整个链条上的供应商、制造商、分销商、零售商，直至最终用户连接到一起，形成一个功能齐全的网链结构。

供应链上企业间的分工使得有效分工理论由企业内部成员这一微观主体层面，上升到独立企业这一中观主体层面。这对于过去大而全的企业来说，可以集中资源致力于自身最具优势的领域，而将其余业务交由外部企业来承担；对于中小企业而言，通过承接大企业生产外包或全球化采购模式下的外包业务，同样可以做到“小而强大”，提高自身竞争力。然而目前不论是从供应链管理的实践还是理论研究来看，上述企业在供应链管理中做得比较好的是供应链三个“流”中的前两个流，即信息流和货物或服务流，而表现不尽如人意、受关注最少的则是资金流。这在很大程度上制约了供应链管理在企业降低运营成本、提高运营绩效中所发挥的作用。

实际上，供应链金融正是为了解决供应链管理中的“木桶短板效应”而发展起来的。对于供应链金融的含义，不同的学者给出了不同的答案。胡跃飞、黄少卿（2009）认为供应链金融是人们为了适应供应链生产组织体系的资金管理而开展的资金与相关服务定价与市场交易活动；牟龄（2006）认为供应链金融是银行将核心企业和上下游企业联系在一起提供灵活运用的金融产品和服务的一种金融服务。笔者认为，供应链金融是基于供应链上下游企业之间建立的长期合作关系，为了消除链上企业，尤其是中小企业的资金瓶颈，提升整个供应链的竞争力，以银行围绕核心企业向供应链上各企业授信为核心的一种融资服务过程。供应链金融尤其适用于中小企业融资。因为，银行围绕核心企业的授信，正是对应于中小企业与大型企业共建信誉来补足中小企业信用，实现中小企业信贷融资的关键环节。

供应链金融并不是传统的对单一业务或企业授信融资，而是采用“1+N”融资模式，评估整个供应链及其交易活动的信用风险。其中的“1”代表的是供应链中的一家核心企业，“N”代表的则是供应链上，围绕一家核心企业的众多供应商、制造商、分销商、零售商甚至最终用户。在“1+N”模式中，供应链上的众多中小企业建立在与核心大企业的长期合作关系之上的信誉共建机制，能够弥补银行等金融机构与中小企业间的信息不对称，改善银行等金融机构对中小企业信用风险评估，突破中小企业信贷配给约束，解决中小企业信贷渠道受阻问题。其中，核心企业实际上起到的是对中小企业的反向担保、信用质量提升作用，当然一旦信誉共建机制破裂，核心企业就有责任成为银行等金融机构的追偿对象，这样一来又化解了银行等金融机构的信用风险。

二、供应链金融演化博弈模型

（一）理论基础 演化博弈论源于生物进化理论，其在分析社会习惯、规范、制度或体制形成的影响因素及其自发形成过程中取得了令人瞩目的成绩。同时，演化博弈的研究成果为群体演化的研究提供了有效分析工具，为群体演化实施提供了合理的方法论，从而为供应链金融系统的演化分析提供了理论依据。演化博弈论假定，在有限理性的博弈双方重复博弈过程中，在有限理性引起的差错与偏差的干扰下，仍能够恢复的均衡策略是演化稳定策略均衡（Evolutionarily Stable Strategy，简称ESS）。该均衡是博弈双方动态重复博弈的过程中形成的。

（二）银行与中小企业演化博弈模型 具体如下：

（1）模型假设。对于中小企业有两种融资情况，一种是“游离”，即中小企业不参与到供应链融资模式中，不存在与其保持稳定而长期合作的核心企业，中小企业无法得到供应链融资模式中核心企业给予的反向担保，因而在中小企业违约的情况下，银行无法从核心企业处获得补偿，独立于供应链之外的中小企业违约情况下也几乎没有额外损失；另一种是“不游离”，即中小企业参与到供应链融资模式中，与供应链上的核心大企业有着良好而持久的产供销合作，核心企业在整个供应链融资中起着反担保的作用，当供应链中的中小企业出现贷款违约情况，核心企业将承担弥补银行损失的责任，同时核心企业将放弃与中小企业继续合作，以实现对中小企业失信行为的惩罚。

（2）银行与游离状态下中小企业的演化博弈模型。首先考虑银行与“游离”状态下中小企业之间的2×2 非合作重复博弈，双方的支付矩阵如表1 所示：

表1 银行与游离状态下中小企业之间交往的支付矩阵

其中L 为银行给予中小企业的贷款金额，r 为银行贷款利率，Lr 为银行的贷款利息收益，其大于交易成本c；i 为中小企业将所得贷款用于投资经营所获得的平均收益率，假定i＞r，否则中小企业没有积极性从银行等金融机构处融资并进行负债经营；c 为银行与中小企业达成信贷交易，所需付出的沟通、谈判、信用风险评估等交易成本，并假定双方都需承担此成本。

模型中有两类博弈群体，即贷款银行群体（k=1）及“游离”状态下的中小企业群体（k=2）。银行群体有两种策略，分别是“贷款”（j=1）和“不贷款”（j=2）；“游离”状态下的中小企业同样有两种策略，分别是“守约”（j=1）和“违约”（j=2）。这里两类群体的策略交往可以描述在一个二维平面内，于是状态s=（sjk）=（s11，s21），（s12，s22）可以用［0,1］×［0,1］区域中的一点（p,q）来表示。s11=p 表示银行群体中采取“贷款”策略银行所占的比例；s21=q 表示中小企业群体中采取“守约”策略中小企业的比例，显然s21=1-p，s22=1-q，分别表示银行群体中采取“不贷款”策略及中小企业群体中采取“违约”策略的个体所占比例。

演化博弈中的适应度表示种群中选择某个策略的个体数量在博弈后的增长率，适应度函数可以理解为策略与适应度的函数关系，代表了种群中个体选择某一策略的收益水平，即fk（ej；s）（k=1,2及j=1,2），它表示个体以概率ej（j=1，2）选择策略S 所获得的期望收益。e1=（0,1）表示银行或中小企业以概率1 选择“贷款”或“守约”策略，e2=（0，1）表示银行或中小企业以概率1 选择“不贷款”或“违约”策略。假定，银行群体与中小企业群体在一个“自然”（不考虑其他约束）的环境中进行策略交往。则对于银行群体采取“贷款”及“不贷款”策略的适应度分别为：

f1（e1；s）=q（Lr-c）-（1-q）（L+c）

f1（e2；s）=0

银行群体的平均适应度为：

f1（p；s）=pf1（e1；s）+（1-p）f1（e2；s）

对于中小企业群体，采用“守约”及“违约”策略的适应度分别为：

f2（e1；s）=p（Li-Lr-c）-（1-p）c

f2（e2；s）=p（Li+L-c）

中小企业群体的平均适应度为：

f2（q；s）=qf2（e1；s）+（1-q）f2（e2；s）

根据Malthusian 动态方程，在动态演化过程中，某种策略的增长率等于该策略的相对适应性。于是，银行群体“贷款”策略的增长率（lnp）=p/p 就等于其相对适应性，即p/p=f1（e1；s）-f1（p；s），因此得到：

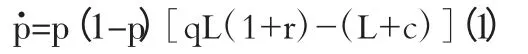
同理，中小企业群体“守约”策略的增长率等于其相对适应性，同样得到：

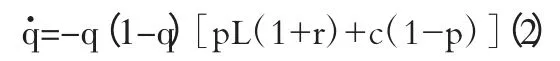
按照Friedman 提出的方法，对于一个由微分方程系统描述的群体动态，其均衡点的稳定性是由这个系统的雅克比（Jacobian）矩阵的局部稳定分析得到的。所以本文使用Jacobian 矩阵的局部稳定分析方法来研究上述方程（1）和方程（2）组成的系统稳定性。

方程（1）和方程（2）组成系统的Jacobian 矩阵为：

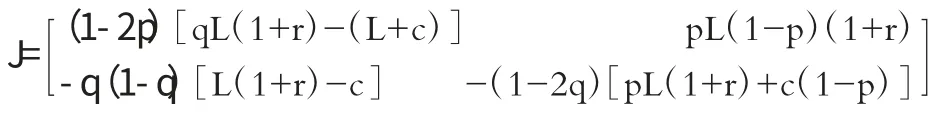
上述Jacobian 矩阵的行列式和迹分别为：

DetJ=-（1-2p）（1-2q）［qL（1+r）-（L+c）］［pL（1+r）+c（1-p）］+pqL（1-p）（1-q）（1+r）［L（1+r）-c］

trJ=（1-2p）［qL（1+r）-（L+c）］-（1-2q）［pL（1+r）+c（1-p）］

则局部均衡分析的结果如表2 所示：

表2 银行与游离状态下中小企业演化博弈局部稳定分析结果

可见，系统的平衡点中，只有（0,0）点是ESS。而（0,1）和（1,0）是鞍点，（1,1）是不稳定平衡点。即只有双方采取“不贷款”和“违约”策略的不合作状态是ESS，而双方采取合作策略是不稳定策略。双方的不合作策略是主导策略，即从任何初始状态出发，系统都将收敛于（0,0）见图1。

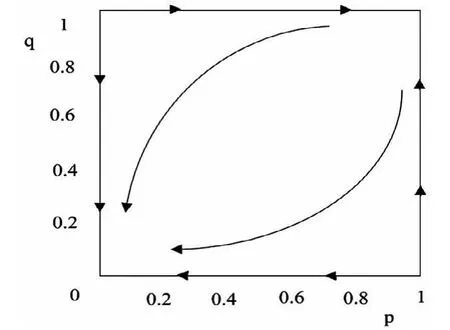
图1 企业游离状态下的系统动态演化相图

当中小企业参与到供应链融资模式中，供应链中的核心企业为中小企业提供反向担保，成为银行在中小企业违约情况下的追偿对象，并在中小企业违约的情况下给予中小企业足够大的惩罚力度，来约束中小企业的行为；同时银行也由于中小企业参与到供应链融资模式中，与核心企业建立信誉共享机制，而对中小企业的信用风险评价得到改善。于是，银行和中小企业的合作（双方分别采取“贷款”及“守约”策略）可能成为双方的主导策略，此时系统将收敛到（1，1）点。

（3）银行与不游离状态下中小企业演化博弈模型。接下来考虑银行与“不游离”状态下中小企业之间的2×2 非合作重复博弈，双方的支付矩阵如表3 所示：

表3 银行与不游离状态下中小企业之间交往的支付矩阵

中小企业在“不游离”状态下，一旦其采取“违约”策略，核心企业将永远拒绝与中小企业合作以惩罚中小企业的失信行为，这使得中小企业损失今后与核心企业的合作收益。假定损失贴现值为，其中为贴现因子，0＜δ＜1］。

基于上述支付矩阵，同样得到银行与“不游离”状态下中小企业群体策略交往的微分方程系统：

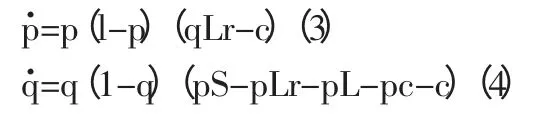
方程（3）和方程（4）组成系统的Jacobian 矩阵为：

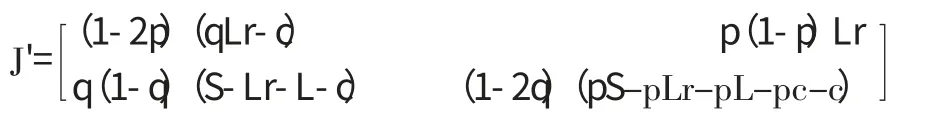
上述Jacobian 矩阵的行列式和迹分别为：

DetJ'=（1-2p）（1-2q）（qLr-c）（pS-pLr-pL-pc-c）-pqLr（1-p）（1-q）（S-Lr-L-c）

trJ'=（1-2p）（qLr-c）+（1-2q）（pS-pLr-pL-pc-c）

为了使博弈双方的支付更加符合实际情况增加约束条件。对于“不游离”状态下的中小企业群体，当供应链上的核心企业给予其违约惩罚后，其收益小于守约时的收益，即Li+L-c-S＜Li-Lr-c，只有这样，“不游离”状态下的中小企业在核心企业介入才后才有积极性采取“守约”策略。于是得到，S＞L（1+r）。当然也可以假定S远比双方的交易成本c 大得多，因为只有这样的损失贴现对中小企业才是有“威慑”的。则此时局部均衡分析的结果如表4 所示：

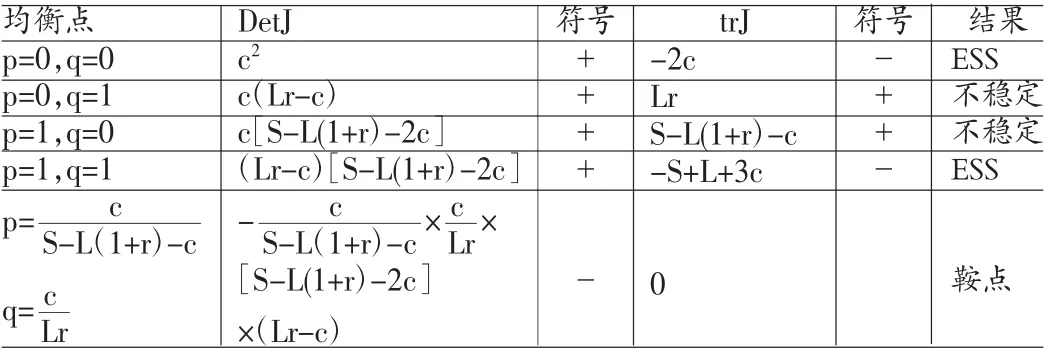
表4 银行与不游离状态下中小企业演化博弈局部稳定分析结果

由表4 可知，系统的5 个局部平衡点仅有两个是稳定的，是演化稳定战略（ESS），他们分别对应于银行与“不游离”状态下中小企业的两种策略模式，即（贷款，守约）与（不贷款，违约）模式。方程（3）和方程（4）组成的系统还有两个不稳定平衡点（p=0,q=1）和（p=1,q=0）以及一个鞍点。

图2 中由2 个不平衡点A、C 和鞍点N 连成的折线可以看作是系统收敛于不同状态的临界线，初始状态在ABCNA 区域时，系统都将收敛到模式（贷款，守约），这是一种双方合作的“理想”状态；而当处于OANCO 区域时，系统都将收敛到模式（不贷款，违约），这是一种不合作的不良“锁定”状态。

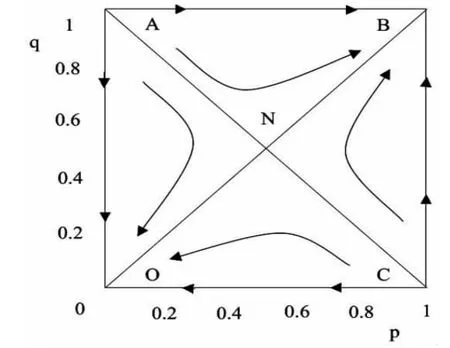
图2 企业不游离状态下的系统动态演化相图

三、演化结果的影响因素

本文使用相图的变化示意图来讨论参数变化对系统演化结果的影响。在鞍点处：

四、结论

从前文的银行群体与中小企业群体间动态博弈分析可以得出，在不对称信息条件下，中小企业征信系统缺失所导致的信用供给不足背景下，要使银行与中小企业双方采取（贷款，守约）这种合作模式，合理的中小企业信用补充机制是至关重要的。合理的中小企业信用补充机制能够消除中小企业信用不足、信贷融资渠道受阻等问题，帮助中小企业克服债务资本融资缺口，在资本市场无法涉足的情况下，极大缓解中小企业发展过程中的资金约束限制。

本文的分析结果显示，供应链融资模式是一种合理的中小企业信用补充机制。其中的关键要素有两个，一是要通过改变传统的信用评价体系，将专注于中小企业自身信用风险的评估，转变为对整个供应链及其交易活动的评估，降低银行对中小企业授信过程中的各项交易成本，从根源上杜绝中小企业信贷融资中的“逆向选择”问题，提升中小企业的信用质量；二是密切供应链中的核心企业与中小企业的合作，充分发挥供应链组织运行的合作效应，提高中小企业“不游离”状态下从与供应链核心企业合作中获得的收益水平，并将这种收益作为诱使中小企业采取“守约”策略的激励因素，通过这种收益诱捕机制，改变银行对中小企业策略选择动机的考量。本文的演化博弈分析进一步表明，银行与中小企业的策略选择更多的是基于对外部因素影响彼此收益考虑之后做出的选择。供应链金融中，核心企业及整个供应链利益关系的介入改变了“不游离”状态下中小企业与银行的外部利益影响因素，驱使双方能够从不合作状态，转化为相互信任的合作状态，这在降低银行信用风险的同时，更大程度上解决了中小企业的融资难题。

［1］胡跃飞、黄少卿：《供应链金融：背景、创新与概念界定》，《金融研究》2009 第8 期。

［2］牟龄：《供应链金融：对中小企业融资的新思维》，《金融时报》2006。

［3］盛昭瀚、蒋德鹏：《演化经济学》，上海三联书店2002 年版。