水平轴潮流能水轮机的流固耦合分析

田美灵，刘雪峰，王晋宝，唐志波，陈正寿，孙忠军

(1.浙江海洋学院海运与港航建筑工程学院,浙江舟山 316022; 2.浙江海洋学院船舶与海洋工程学院,浙江舟山 316022;3.浙江欧华造船股份有限公司,浙江舟山 316101)

水平轴潮流能水轮机的流固耦合分析

田美灵1，刘雪峰2，王晋宝1，唐志波1，陈正寿2，孙忠军3

(1.浙江海洋学院海运与港航建筑工程学院,浙江舟山 316022; 2.浙江海洋学院船舶与海洋工程学院,浙江舟山 316022;3.浙江欧华造船股份有限公司,浙江舟山 316101)

叶轮作为潮流能水轮机捕能的关键部件,其水动力性能以及结构性能会影响水轮机的捕能效果及其结构的安全性。本文以30W的小型水平轴潮流能水轮机为例,分别基于单向流固耦合和双向流固耦合模型对在设计工况下的叶轮水动力性能与结构性能进行了稳态分析,对比研究了两种耦合模型所得到的叶轮捕能系数、叶轮表面压力分布等水动力性能和叶轮应力分布等结构性能,为进一步对叶轮结构优化提供参考依据。

潮流能水轮机;单向流固耦合;双向流固耦合;水动力性能;结构性能

随着经济的发展,人类对能源的需求也在持续增加,由此导致传统能源面临枯竭等问题。然而,潮流能作为一种蕴藏丰富的可再生能源,合理对其开发利用可以有效的缓减能源问题,因此其也受到许多国家的重视。

潮流能水轮机叶轮作为能量捕获的关键部件,人们最关心的是其捕能效果,因此对其多进行水动力性能研究。但是,随着水轮机技术的发展,水轮机也向着大型化发展,其安全问题也越来越受人们重视,除了要对其水动力性能进行研究外,还要考虑其结构性能。而流固耦合正是解决流体和结构相互作用这类问题的,因此将流固耦合技术应用到研究水轮机水动力性能和结构性能的分析中会成为一种必然趋势。

本文以30W的小型水平轴潮流能水轮机为例,利用数值模拟方法对其在设计工况下的部分水动力特性和结构特性进行了单向流固耦合与双向流固耦合分析,并对两种耦合方法下的结果进行了对比分析,进而为水轮机模型优化及制作提供一定的参考依据。另外由于对流固耦合问题进行数值模拟时不仅耗时而且对电脑配置要求高,因此这里只对设计工况下的叶轮性能进行了稳态分析而未考虑其在其它工况下的性能。

1 流固耦合基本理论

流固耦合问题是计算流体力学(CFD)与计算固体力学(CSM)交叉生成的一门学科,同时也是多物理场研究的一个重要分支,研究的主要是可变形固体在流场作用下的各种行为以及固体变形对流场的影响。由于流固耦合问题同时考虑了流体特性和结构特性,可以有效地减少分析时间并且节约成本,而且其分析结果比较接近于物理现象本身的规律,因此,流固耦合分析近年来在工程设计中的应用越来越广泛。流固耦合问题在自然现象中本来就存在,再加上计算流体力学(CFD)和计算固体力学(CSM)快速发展,才使得流固耦合分析方法实现并得到广泛的应用。

1.1 流体控制方程

流体流动遵守质量守恒、动量守恒和能量守恒。对于一般的可压缩牛顿流体来说,守恒定律主要通过如下控制方程描述。

质量守恒方程:

动量守恒方程:

其中,t表示时间,ff是体积力矢量,ρf为流体密度,v为流体速度矢量,τf为剪切力张量,如下,

式中,p为流体压力,μ为动力粘度,e为速度应力张量且

1.2 固体控制方程

对于固体部分的控制方程,由牛顿第二定律得出:

式中,ρs为固体密度,σs为柯西应力张量,fs为体积力矢量, 为固体当地加速度矢量。

1.3 流固耦合方程

在流固耦合分析中,流体域与固体域在流固耦合交界面上要同时满足运动学条件和动力学条件,要遵循基本的守恒原则,即在流固耦合交界面上要满足流体与固体应力(τ)和位移(d)等变量的相等或守恒,如下,

式中所有下标f表示流体域,所有下标s表示固体域。

目前用来求解流固耦合问题的方法主要有两种:直接解法和分离解法。直接解法是在同一求解器中同时求解流体和固体的控制方程,不存在时间滞后问题,因此在理论上很先进、很理想,但在实际中却很难将CFD和CSM技术真正结合到一起,而且同步求解既耗时又很难收敛;而分离解法与直接解法不同,它是按顺序在同一或者不同求解器中分别求解流体方程和固体方程,同时通过耦合交界面相互传递流体域和固体域的计算结果。等到这一时刻收敛达到要求,再进行下一时刻的计算,依此而行求得最终结果,存在时间滞后问题并且在耦合交界面上的能量不完全守恒,但是它最大地利用了已有计算流体力学和计算固体力学两门学科。另外分离解法需要的内存也较低,可以用来解决大规模问题[1]。目前,几乎所有的CAE商业软件,对于流固耦合问题都采用分离解法进行求解。

1.4 单向与双向流固耦合分析

前边已提到过,几乎所有商业软件对于流固耦合问题都采用分离解法也即载荷传递法求解。根据数据传递形式,可以将流固耦合分为单向流固耦合和双向流固耦合。

对于单向流固耦合分析,在耦合交界面出数据的传递是单向的,一般是将流体域计算结果传递到固体域进行结构分析,而不把固体结构分析结果传递给流体域,因此可以认为,只有流体域对固体域有影响,而固体域对流体域几乎没有影响。

对于双向流固耦合分析,在耦合交界面处的数据传递是双向的,即在流体域计算结果向固体域传递的同时也会有固体域计算结果向流体域传递,流体域与固体域相互作用、相互影响。

2 流固耦合分析方法

根据文献[2]和[3]选取设计流速0.8m/s。选取叶片数5。根据文献[4],选取叶尖速比3.0,捕能系数0.4,并且可以通过计算得到叶轮半径为0.3m。具体参数见表1。

表1 潮流能水轮机叶片设计参数Tab.1 Designing parameters of tidal current energy turbine blades

2.1 模型的建立

根据叶轮设计参数,建立起叶轮几何模型。对于流场模型,采用圆柱内部挖去叶轮来实现,这样圆柱内部型腔是叶轮外形[5]。其中,流体域包括静止域与旋转域,旋转域只要包含了叶轮模型即可。

2.2 叶轮材料的定义

参照文献[6],选用环氧玻璃钢作为叶轮材料,其材料参数见表2。

表2 叶轮材料参数Tab.2 Parameters of turbinematerial

2.3 网格的划分

在进行数值模拟计算时,要求网格的划分要适应区域中物理场的变化情形,在变化比较剧烈的地方网格要适当稠密一些,在变化平缓的地方网格可以稀疏一点。采用四面体网格对流体域进行划分,在叶轮附近要适当加密,划分后网格数量为3 156 035,其中旋转域网格数量为2 856 936,静止域网格数量为299 099;同样采用四面体网格对固体域进行划分,因为这样可以较好的适应叶轮结构比较复杂的形状,最后得到网格数量为153 560。

2.4 边界条件的设置

对于结构模型,叶轮转速可以根据尖速比求得,并且对叶轮径向和轴向进行位移约束使其只能绕中心轴旋转,同时定义好叶轮表面以便施加流场载荷。

对于流场模型,在设定边界条件时,采用速度入口边界,大小已知。采用压力出口边界,出口相对压力为0 Pa。旋转域转速、转向都可以知道,其中流体域内腔随旋转域旋转,设置为固壁边界,且与叶轮结构表面组成一对流固耦合面。

2.5 湍流模型的选取

本文进行CFD模拟计算时,选用SST湍流模型。SST湍流模型属于混合模型,它具有k-ω模型在近壁面区域附近模拟准确性和k-ε模型在处理主流区域时计算代价小的优点[7]。由于潮流能水轮机在工作时,叶片周围的流场会出现边界分离,且主要基于翼型绕流,靠来流对叶片作用产生力矩使叶轮旋转,因此,采用SST模型更适合来模拟此问题。对SST模型,其k和ω运输方程如下:

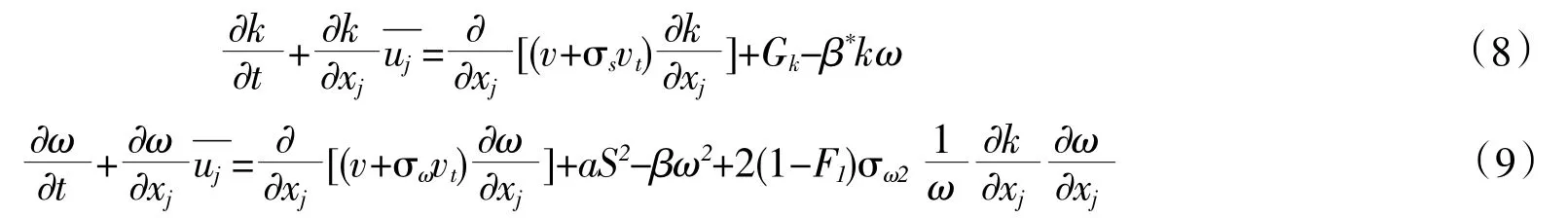
其中,

湍流粘性系数为

混合函数为

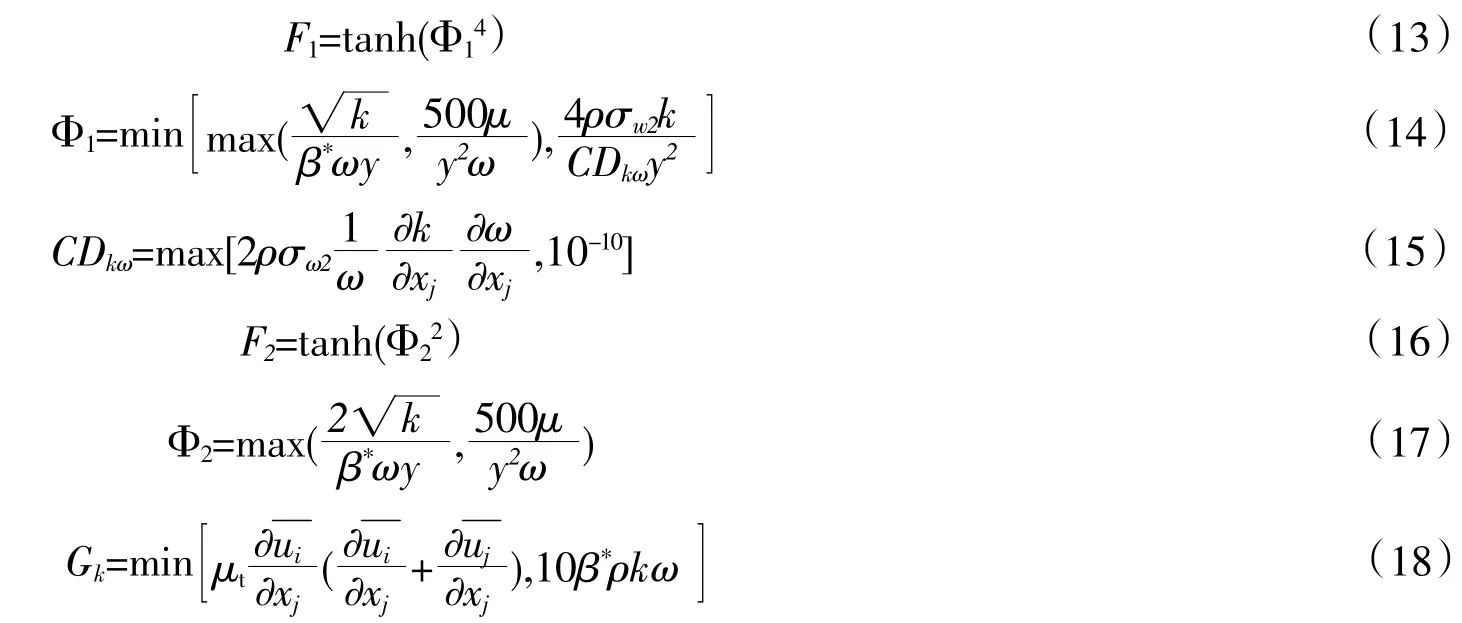
3 单、双向流固耦合结果的对比与分析

3.1 轴功率、捕能系数、推力系数的对比分析

在单、双向流固耦合两个计算过程中监测了叶轮所受轴向推力与转矩,图1、图2分别给出了在单向与双向流固耦合过程中叶轮所受轴向推力和转矩。由图1可知,对于单向流固耦合,在设计工况下叶轮所受轴向推力大小为74.546 N,转矩大小为4.181 3 N·m;由图2可知,对于双向流固耦合,在设计工况下叶轮所受轴向推力大小为75.123 N,转矩大小为3.807 6 N·m。由此可以求的两种情况下对应的叶轮轴功率、捕能系数和轴向推力系数,对应公式如下。轴功率公式:

捕能系数公式:

轴向推力系数公式:

图1 单、双向流固耦合叶轮所受轴向推力与转矩Fig.1 Thrust force and torque of turbine under one-way and double-way FSI

根据以上公式及图1可以求得单向流固耦合和双向流固耦合情况下的计算结果,见表3。

表3 单、双向流固耦合计算结果对比Tab.3 Comparison of results under one-way and double-way FSI

由表3可知,与设计功率30W和捕能系数0.40相比,通过单向流固耦合方法得到的轴功率和捕能系数都相对偏大,而通过双向流固耦合方法得到的结果与设计所选参数更接近,这也说明与单向流固耦合相比,双向流固耦合所模拟出的情况与设计工况更接近。另外,对比单、双向流固耦合方法所得轴向推力系数可以看出,双向流固耦合所得结果较单向流固耦合结果稍大,对应轴向推力也较大,这也对叶轮结构的安全性会有一定的影响,其值过大可能导致叶轮结构的破坏,因此叶轮结构需要满足强度要求,后边将会涉及到叶轮结构强度分析。

3.2 流场压力的对比分析

图2和图3分别给出了利用单向流固耦合和双向流固耦合方法得到的在设计工况下叶轮叶片表面流场压力的分布云图。

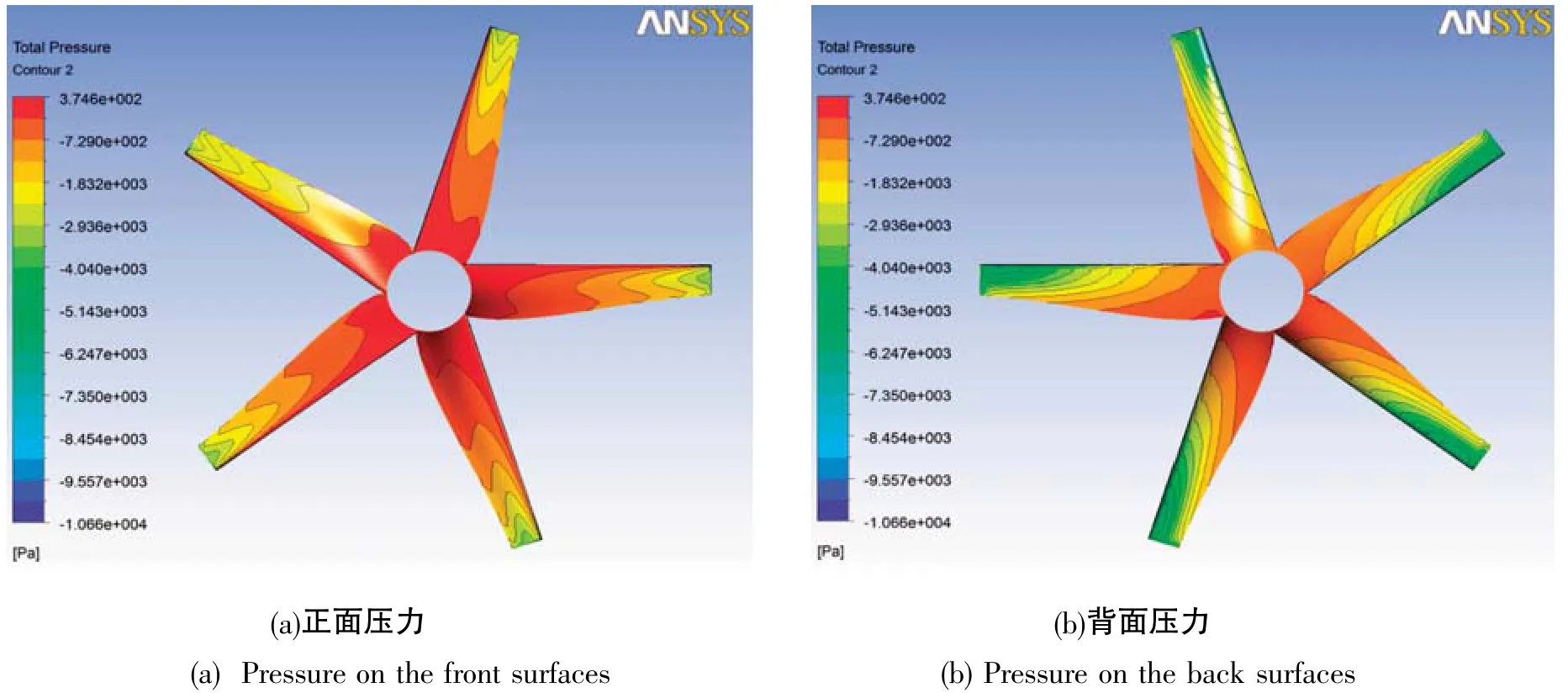
图2 单向流固耦合叶片表面流场压力图Fig.2 Fluid pressure contour on the blades surface under one-way FSI

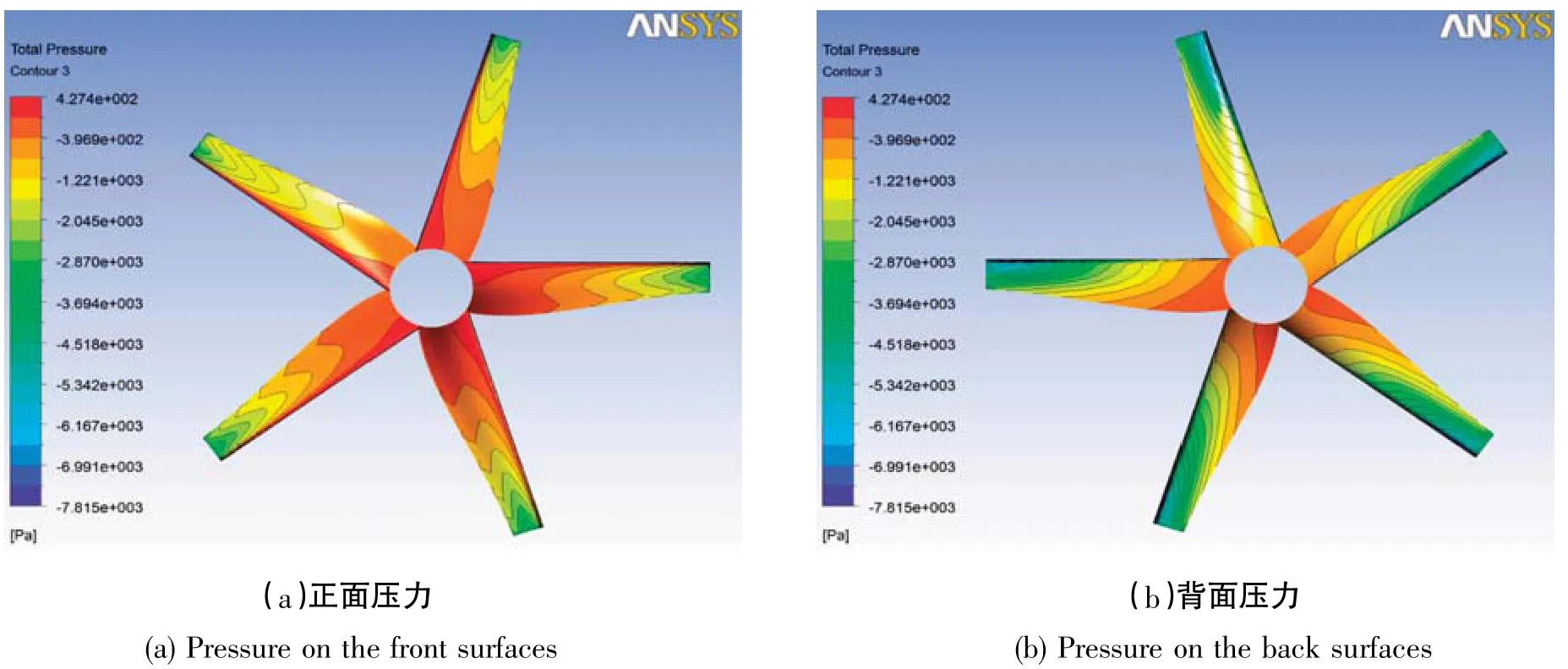
图3 双向流固耦合叶片表面流场压力图Fig.3 Fluid pressure contour on the blades surface under double-way FSI

从图2、图3可以看出,叶片正面(压力面)压力均大于叶片背面(吸力面)压力,正是由于压力面和吸力面之间的压力差才使得叶片翼型受到升力与阻力作用,进而使得叶轮旋转。此外,由于叶轮在以一定转速工作时,半径小的地方线速度一定小,因此在叶尖处的线速度必然大于叶根处的线速度;另外,由于在叶轮旋转时,会使得叶轮周围水流也产生旋转,因此会对来流速度产生影响,且在叶片处的流体实际速度为叶片处水流旋转线速度与水流来流速度的合速度,因此在叶片处的流场速度由叶根到叶尖是逐渐增加的。由于在叶根处流体速度相对最小、叶尖处流体速度相对最大,因此叶片表面的流场压力在叶根处相对最大而在叶尖处相对最小。

可以看到,对于单向流固耦合,叶片表面流场压力最大值约为3.75×102Pa,最小值约为-1.07×104Pa;而对于双向流固耦合,叶片表面流场压力最大值约为4.27×102Pa,最小值约为-0.78×104Pa。可以看出在双向流固耦合情况下,叶片表面流场压力最大值较大。另外,对于压力面,在靠近叶片前缘处的压力都比靠近叶片后缘处的压力大;同时对于吸力面,在靠近叶片前缘处的压力则小于靠近叶片后缘处的压力,根据伯努利原理可知这也与二维翼型表面压力分布一致,而且通过比较图2、图3可以看出在双向耦合的情况下,这种现象表现的更为明显。

3.3 叶片结构应力、应变及变形的对比分析

图4、图5和图6分别给出了单、双向流固耦合对应的叶轮叶片的应力、应变和总变形图,从图中可以看出叶片应力、应变在叶根处最大,在叶尖处最小;而对于总变形则是在叶尖处最大,在叶根处最小。且对于单向耦合,叶片最大应力值约为2.54×106Pa,最小应力值约为128.52 Pa,最大应变值约为0.13×10-3m/ m,最小应变值约为6.70×10-9m/m;而对于双向耦合,叶片最大应力值约为2.58×106Pa,最小应力值约为145.7 Pa,最大应变值约为0.13×10-3m/m,最小应变值约为7.44×10-9m/m。另外,由于叶片叶根被固定而其它部分悬空,且展向长、弦向短,而且叶轮在工作时受到水流的轴向推力作用,除此之外还受到转矩作用,因此叶片既有轴向上的变形而且有其旋转方向上的变形。且从叶片总变形图总可以知道,在水流作用下,叶片最大总变形对于单向耦合其值约为0.67×10-3m,对于双向耦合其值约为0.69×10-3m。

综上可知,在双向流固耦合情况下,与其对应的叶片应力、应变及最大总变形都稍比单向流固耦合情况下大,但是叶片最大应力、最大应变以及最大总变形的值都很小,根据叶轮材料特性可以知道叶片结构满足强度要求。

图4 单、双向流固耦合叶片应力图Fig.4 The blades stress under one-way and double-way FSI

图5 单、双向流固耦合叶片应变图Fig.5 The blades strain under one-way and double-way FSI

图6 单、双向流固耦合叶片总变形图Fig.6 The blades total deformation under one-way and double-way FSI

4 结论

通过对在设计工况下的叶轮分别进行单向和双向流固耦合对比分析,可以得到如下结论:

(1)通过对比两种耦合情况下叶轮的轴功率、捕能系数可知道,双向流固耦合模拟情况与设计工况更接近,其中利用双向耦合方法得出的功率比设计所选功率大1.53%,捕能系数比设计所选值大5%;而利用单向耦合方法得出的功率比设计所选值大11.5%,捕能系数比设计所选值大15%。

(2)通过对比两种耦合情况下叶片表面的流场压力知道,叶片表面的流场压力分布与二维翼型表面的流场压力分布一致,即在压力面上靠近叶片前缘处的流场压力大于靠近叶片后缘处的流场压力,而在吸力面上靠近叶片前缘处的流场压力则小于靠近叶片后缘处的流场压力;同时,叶根处的流场压力相对最大,而叶尖处的流场压力相对最小;此外,利用双向流固耦合方法得到的流场压力最大值要比利用单向流固耦合方法得到的流场压力最大值大。

(3)利用双向耦合方法得到的叶轮轴向推力系数较单向耦合方法所得值大,即叶轮受到的轴向推力更大,所以要求叶轮结构强度要满足要求。同时通过对比单、双向流固耦合下叶片结构的应力、应变以及总变形可知,叶片的最大应力、最大应变均发生在叶根处,而最大总变形发生在叶尖处,而且这些值在双向耦合情况下要稍大于在单向耦合情况下的值,但是这些值都很小,根据所选叶轮材料特性可以知道叶片结构强度满足要求。

[1]宋学官.ANSYS流固耦合分析与工程实例[M].北京：中国水利水电出版社，2012.

[2]王俭超.水平轴潮流水轮机叶片设计和模型试验研究[D].青岛：中国海洋大学，2011.

[3]徐学涛.水平轴潮流能发电机械叶片设计及特性分析[D].杭州：浙江大学，2012.

[4]赵丹平.风力机设计理论及方法[M].北京：北京大学出版社，2012.

[5]陈海萍.风力发电机叶片的流固耦合分析[J].机床与液压，2010，38（19）：79-82.

[6]武玉龙.3 MW风力机叶片设计建模与模态分析[J].机械研究与应用，2013，26（3）：4-7.

[7]荆丰梅.潮流能水轮机单向流固耦合计算方法[J].振动与冲击，2013，32（8）：91-95.

Fluid-structure Interaction Analysis on Horizontal Axis Tidal Current Energy Turbine

TIANMei-ling1，LIU Xue-feng2，WANG Jin-bao1，et al
(1.School of Shipping and Ports Architecture Engineering of Zhejiang Ocean University，Zhoushan 316022; 2.School of Ship and Ocean Engineering of Zhejiang Ocean University，Zhoushan 316022，China)

As the key component of tidal current energy turbine，the hydrodynamic and structural performance of the turbine will have some effect on the turbine＇s energy-catching efficacy and its safety.In this paper，taking 30W small horizontal axis tidal current energy turbine as an example，its hydrodynamic and structural performances in designed working condition were analyzed based on one-way and double-way fluidstructure interactionmodes，respectively.Then，the hydrodynamic performance，such as energy-catching coefficient and pressure distribution on the surface，and its structural performance，such as the stress distribution，are compared and analyzed，which result from two kinds of couplemodes.Finally all the resultswill be useful for the further optimal design of the turbine.

tidal current energy turbine；one-way fluid-structure interaction；double-way fluid-structure interaction；hydrodynamic performance；structural performance

TH212

A

1008-830X（2014）05-0430-07

2014-03-20

国家海洋局项目(ZJ2010ZC01);舟山市科技局项目(2013C41014);浙江海洋学院校级课题

田美灵(1977-),女,山西原平人,讲师,研究方向:海洋能源开发与利用.E-mail：eileen@zjou.edu.cn