有限振幅扰动下高超声速钝楔绕流感受性
2014-11-05唐小军王振清孟祥男吕红庆
唐小军 王振清 孟祥男 吕红庆
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨150001)
由于流场中的扰动对高超音速飞行器的升阻力及热流等气动热力学特性的影响,飞行器的性能显著地受到制约,而流场中的扰动多种多样且广泛存在,例如在高超音速飞行器热防护设计的前缘人工引入反向喷流[1-4],飞行中遭遇突风[5]及爆炸波[6]等情形,飞行器表面的变形和颤振[7]引发边界层的分离和层流-湍流转捩等.这些扰动对流场流动情况、飞行器气动热力学特性及结构强度有着显著影响,且它们的影响也各不相同.流场中扰动形式的多样性和扰动影响的不确定性给飞行器的设计带来了问题.在当前的飞行器设计中,为了确保安全,往往要求更高的安全系数,准确分析扰动对流场的影响机理将会给飞行器设计带来很大的改进.因此,研究扰动与流场的干扰及其对流场稳定性特征的影响具有重要的现实意义.诸多学者做过扰动方面的研究[8-13],A.V.Fedorov 和 A.P.Khokhlov[8]结合渐近线法和数值计算研究了高超音速平板边界层对壁面扰动的感受,在他们的研究中,包括壁面振动、吹吸及温度扰动被考虑,并得出边界层对壁面吹吸扰动的感受强于壁面振动和温度扰动.通过求解可压缩线性化 N-S方程,M.R.Malik等[9]研究了马赫数为8的来流绕尖楔流动对3种外加扰动的响应,发现不同的扰动在边界层产生相同形式的不稳定波.A.A.Maslov等[10]通过应用高阶激波捕捉格式求解了非定常N-S方程,研究了马赫数为21的平板流动边界层扰动的演变.T.Anatoli等[11]运用模态分解方法对在高超音速绕平板和尖楔流动边界层下游的吹吸扰动进行了直接数值模拟,以研究壁面吹吸扰动对高超音速边界层的影响.但大部分都集中在讨论连续的微弱的扰动对层流-湍流转捩及转捩位置的影响[12-13],而且通常研究的是非定常流达到时间周期后的状态[14],很少有研究专注于数值模拟脉冲波扰动及扰动波的演变,而流场中脉冲波扰动也是存在的,如飞行器遭遇爆炸波等情形,同时,脉冲波和连续扰动波情形边界层扰动波的演变及边界层稳定性特性有着显著的不同.鉴于高超音速边界层扰动波演变对边界层稳定性有很大影响,并且扰动波演变机理依然不完全明白,因而,高超音速边界层对脉冲波的感受性及边界层稳定性的研究可为边界层稳定性研究、层流-湍流转捩预测及气动设计提供一个新的视角,目前这一领域仍缺乏系统的研究.
本文为了探究自由流脉冲波作用下高超音速流场感受性特征,基于马赫数为6的自由来流,0°攻角及8°半楔角的钝楔,采用高阶有限差分法来直接数值模拟慢声波脉冲钝楔高超音速非定常流场,并采用傅里叶频谱分析方法讨论了边界层内扰动波模态演变.
1 控制方程和数值方法
1.1 控制方程
为了进行流场数值计算,将N-S方程由笛卡尔坐标系xi转换为一般曲线坐标系:

式中,J为坐标变换的雅可比矩阵;U为状态矢量;t为时间;为对应于一般曲线坐标下坐标轴方向的无黏通量项;为对应于一般曲线坐标下坐标轴方向的黏性通量项;φi为一般曲线坐标系的坐标方向.
具体的转换过程如下:
φi(x1,x2)是xi的单值连续可微函数,则有


式中Fj和Fvj分别为笛卡尔坐标系下的无黏项和黏性项.
1.2 数值方法及其验证
不连续函数的高阶逼近在不连续区域将会产生数值震荡,且震荡行为随阶数的增加而增大[15],而间断性是高超音速绕钝楔流与脉冲波干扰的非定常流场的重要性质.由于能够使高阶逼近时在间断区域抑制数值震荡且在连续区域保持良好的精度,WENO格式及改进的WENO格式在复杂可压缩流动的高阶精度直接数值模拟中被广泛使用[16].由于文献[17]改进的 WENO 格式在保持高阶精度和抑制数值震荡方面更为优越,因此,为了准确模拟高超音速脉冲扰动非定常流场,本文采用高阶精度有限差分方法直接求解一般曲线坐标系下N-S方程,通过Steger-Warming矢通量分裂方法将N-S方程无黏项分裂为正通量项和负通量项,并对其采用五阶迎风加权本质无振荡(WENO)格式离散,这使得该方法具有高阶逼近且能够很好地抑制数值振荡和数值耗散[17].同时采用六阶精度中心差分格式对黏性项进行离散和三阶TVD龙格-库塔法进行时间推进.具体离散格式如下.
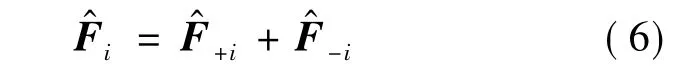
对于正通量项和负通量项,五阶迎风离散格式分别为

对于黏性项,六阶中心差分格式:
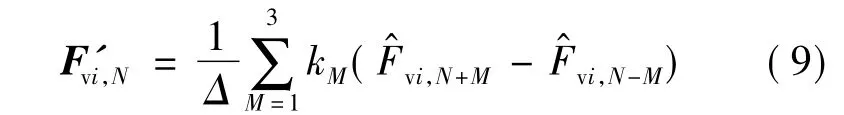
对于时间项,采用三阶 TVD龙格库塔法(Runge-Kutta)离散,如下所示:

用上述方法模拟Lobb等的马赫数为7.1的0°锥角钝体实验模型[18]以验证方法的有效性,如图1所示.本文计算的激波位置与实验结果拟合得很好.同时用本文的数值方法计算了文献[19]中的高频自由流快声波作用下马赫数15的非定常来流绕5°半锥角钝锥算例,计算结果与文献[19]的计算结果拟合得很好,如图2所示.因此本文的数值方法是可靠的.
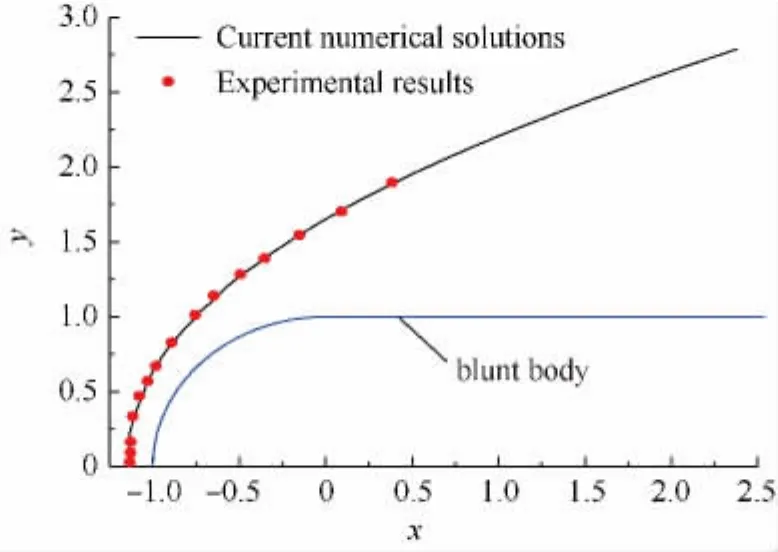
图1 激波脱体位置与文献[18]实验结果比较

图2 边界层二阶压力扰动模态与文献[19]结果比较
2 计算条件与模型
在本文的研究中,考虑了马赫数为6的自由来流绕钝楔流动,计算模型半楔角θ=8°球头半径rn=1 mm的钝楔,图3为计算模型及示意图.计算域上游采用来流条件,出口条件采用外推方法,壁面采用无滑移、无穿透和绝热条件,考虑到对称性,对y=0边界采用对称边界条件.为了捕捉头部强激波和边界层,采用网格拉升的方法对球头部区域及壁面附近的网格进行了局部加密,网格数为300×120,这样的网格密度与文献[19-20]类似模型的高超音速非定常流场直接数值模拟研究中的网格密度相当,甚至更密集.鉴于文献[19-20]等研究中更加微弱的扰动波被精确捕捉,关于网格密度验证这里不再敷述.本文定义流场变量非定常扰动量 L'(x,y,t)=L(x,y,t) -L0(x,y),其中 L(x,y,t)为非定常流场的瞬时参数,L0(x,y)为无扰动波的定常流场参数.

图3 计算模型及示意图

来流温度T=69 K,攻角为0°,基于自由流参数和球头半径rn决定的雷诺数,Ren=ρ0rnu0/μ0=10000,其中 ρ0,u0,μ0分别为来流密度、来流速度、黏性系数.本文对参数进行了无量纲处理:u/u0,v/u0,h/rn,P/(ρ0u0)和 t/(rn/u0),其中 t,u,v,h,P,T和T0分别是时间、坐标x方向速度、坐标y方向速度、特征长度、压强、流场温度和来流温度.首先计算了未受扰动的定常流场,然后待稳态流场迭代收敛后,在无量纲时间t=40.0时,在计算域外边界引入一个时长2(u0/rn)的1/2个周期正弦形式的慢声波脉冲扰动,其形式如式(11)所示,t1=40.0,t2=42.0.式中,扰动振幅 A=8 ×10-2,波数 k=3.1446 ×10-4,广义频率 F=50π,Ma=6.0.
3 结果与讨论
3.1 扰动波对高超音速流场的影响
图4a~ 图 4d 分别为 t=42.5,44.5,46.5,48.5时刻,在受到形如式(11)所示的脉冲作用后流场瞬态压力扰动云图.图4显示,当来流脉冲波进入流场,首先与弓形激波相互作用.在遭遇慢声波脉冲时,弓形激波变形并向外凸起,其附近的压力也显著地受来流慢声波脉冲扰动的影响.由于激波的变形,激波向外凸起区域S1(下同)的压力显著地增大,而弓形激波下方的流场压力显著地变小,其变小的幅值远大于来流压力扰动值,显然,来流扰动被显著放大.换句话说,扰动波与弓形激波的作用产生了强扰动波.由图4a~图4d可以看到,扰动波与弓形激波的作用产生的强扰动波由流场上游向下游传播,在壁面附近,即边界层内的压力也有明显的变化,如图4c、图4d中P1—P2—P3是一个变小—增大—变小的3个相邻的边界层区域.来流扰动波与弓形激波干扰形成的边界层内外的压力扰动模态存在明显差别.
图5a~图5b分别为 t=46.5,48.5时密度扰动 ρ'(x,y,t)云图,图 5c ~ 图 5d 分别为 t=46.5,48.5时温度扰动 T'(x,y,t)云图.图 5a、图 5b 中可以看到流场密度在弓形激波凸起区S1密度增大.随着扰动波从上游流场向下游流场传播,边界层外的流场密度扰动存在主要的2个特征区域,即图5b中的D1和D2区,D1区密度显著减小,而D2区密度增大.即来流脉冲波与弓形激波相互干扰后,弓形激波下方的流场密度首先显著地变小,随着扰动向下游流场传播而远离,该区域的密度将会增大.相对于激波附近流场密度显著变化,边界层内密度受脉冲波的影响小很多.图5c、图5d显示,温度与密度一样受扰动的影响变化很大.在脉冲扰动波作用下,边界层外与弓形激波之间的高超音速流场温度扰动存在主要的2个特征区域,即图5d中的T1和T2区,T1—T2依次增大—减小,这与流场密度扰动变化趋势类似,而边界层内温度扰动模态非常复杂.需要指出的是D1,D2,T1和T2均呈斜条带状,从流场上游到流场下游,该条形区域变长.这是由于来流扰动通过激波减速,离壁面越远,流场来流方向速度越大,正是这样导致了扰动向下游传播速度的差异引起的.由于自由流扰动经激波干扰后进入边界层,并会与边界层相互作用诱导出新的扰动[21],而热力学参数扰动(变化)是边界层扰动的主要形式.由图4~图5可以看到,脉冲波作用下,边界层压力和温度显著变化,而压力和温度分别是边界层内力学机制、热特性的特征参数,显然,自由流脉冲扰动改变边界层强剪切流动热力学机制,而热力学机制被认为对边界层稳定性有着重要影响[21].

图4 不同时刻压力扰动P'(x,y,t)云图

图5 密度扰动 ρ'(x,y,t)及温度扰动 T'(x,y,t)云图
图6a~图6d分别为对应 t=42.5,44.5,46.5,48.5时刻的速度扰动云图.从云图中可以看到在脉冲作用下,在脉冲波与激波干扰区域、边界层与激波之间流场及边界层内速度显著变化,来流扰动波与弓形激波干扰形成的边界层外的速度扰动模态和近壁面边界层内形成的速度扰动模态存在明显分界.边界层速度扰动等值线梯度很大,这说明了慢声脉冲波作用下的钝楔高超音速绕流的边界层内存在复杂干扰,由于存在反射波的作用,边界层内速度扰动模态变得更为复杂.

图6 不同时刻速度扰动云图
由图4~图6可以看到,来流脉冲扰动波与弓形激波干扰后形成的边界层外的扰动波与近壁面区域内由外扰动波所形成的边界层扰动波,两种波模态存在明显差别.来流扰动波与弓形激波干扰进入流场,一部分波将会由流场上游向下游传播,还有一部分波将会在激波与壁面之间往复振荡[21],如图3所示.对于来流连续扰动波这种往复振荡会一直持续,但对于脉冲波,由于被黏性耗散的作用这种往复振荡次数是有限的.需要指出的是,图4~图6中存在反射波引起的等值线,如图中F1,但仅限于弓形激波附近,这是因为扰动波经激波反射将会被放大[21],经弓形激波反射后在流场下游传播过程中存在耗散作用.下面将分析扰动波及反射波与边界层的干扰及边界层内扰动模态的演变.
3.2 边界层扰动波的演变
图7给出了不同时刻壁面气动热力学参数扰动分布.在来流脉冲扰动作用下,摩擦系数先变小再增大,其变化趋势类似来流脉冲扰动.然而,当脉冲扰动完全通过时由来流脉冲扰动引起的影响没有消失,参数受扰动影响的幅值将经历一个阻尼振荡过程,直到幅值完全消失,这是由于一部分扰动波在壁面和弓形激波之间往复振荡形成的.
由图7a可以看到,在来流慢声波脉冲扰动的作用下,壁面摩擦系数C'f在球头部的变化趋势与非头部区域不同,这是由于这两个区域的构型差异导致它们之间的流场差异,特别是弓形激波(头部近似正激波),进而使其与来流的慢声波脉冲的之间的相互作用产生了差异.
图7b、图7d和图7e显示不同时刻的壁面ρ'(x,y,t),T'(x,y,t),P'(x,y,t)分布,这些热力学参数的变化与壁面摩擦系数的变化呈现一个相似的变化趋势.但它们之间也有些细微的差别,壁面摩擦系数、密度、压力和温度的扰动幅值彼此之间差异明显,摩擦系数、密度、压力在球头部的扰动幅值要大于温度在头部的扰动幅值,来流慢声波脉冲扰动对壁面摩擦系数、密度、压力在球头部与非头部区域的影响差异很大,而对温度在头部和非头部区域的影响差异则相对较小.图7显示头部壁面压力扰动最大,这说明,虽然可压流动中任何一种来流扰动与激波干扰将会产生3种独立模态:声波模态、熵波模态和涡波模态[22],但球头区边界层感受到很强的压力扰动即声波扰动.
由图7可知,在自由流作用下,边界层流场参数显著改变,特别是,摩擦系数作为一个表征剪切流动的重要参数,显然这说明,在自由流作用下的边界层强剪切流动结构已经发生改变.由图7可知,脉冲波作用前后壁温扰动差别明显,说明自由流脉冲波对边界层流动热力学特性影响很大.根据文献[21]的研究,边界层强剪切流动结构的热力学机制将会影响边界层的稳定性甚至层流-湍流转捩.因而下面将会基于边界层扰动波演化分析自由流脉冲波作用下的边界层稳定性特征.
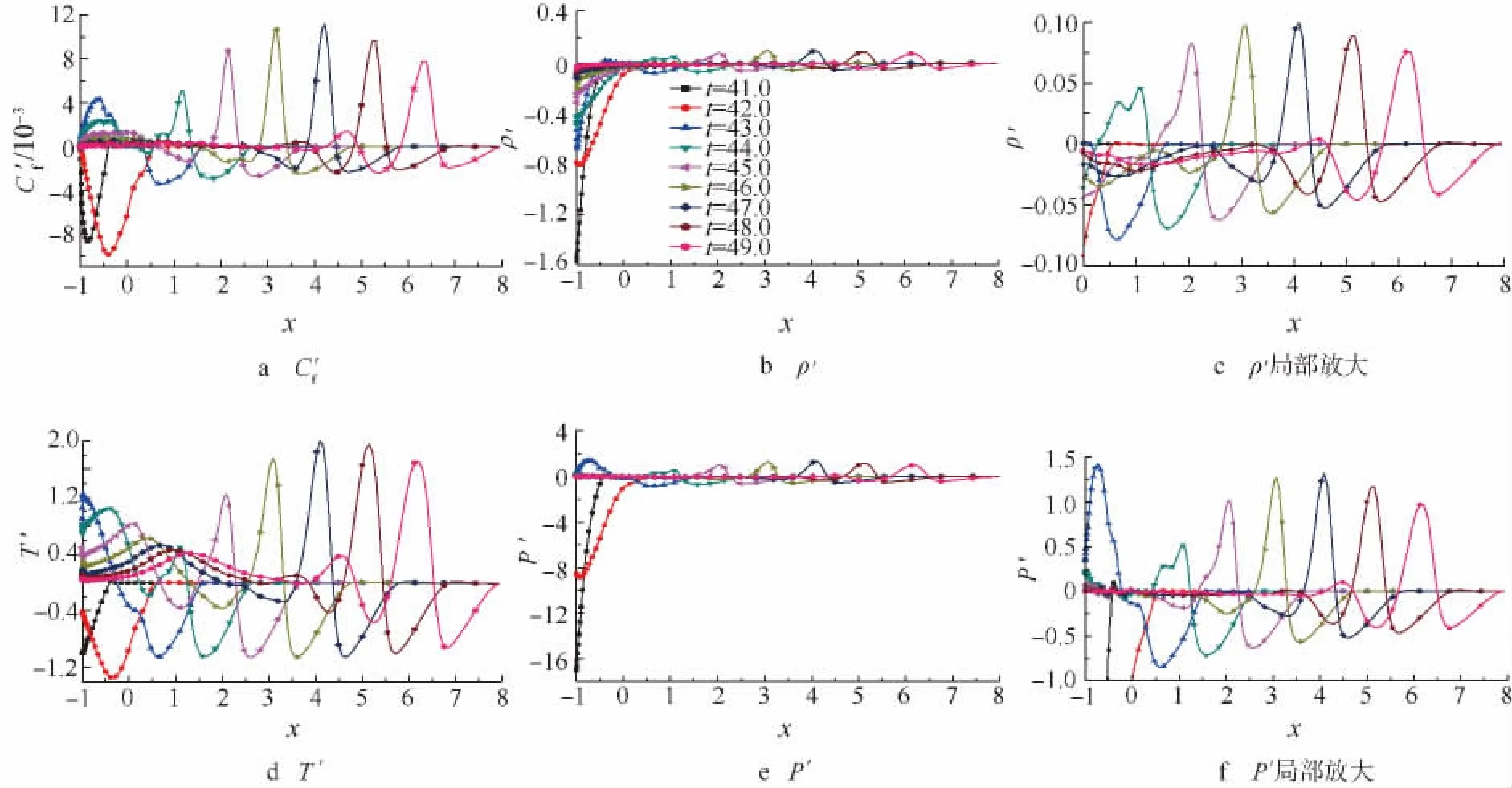
图7 不同时刻壁面气动热力学参数扰动分布
由于外加了脉冲扰动波,如上所述,当遭遇脉冲扰动波后,流场参数将会类似脉冲形式地波动,之后会迎来反射波引起的振荡.在边界层,存在扰动波的传播及反射波的干扰,同时它们与边界层之间也存在复杂的相互干扰作用,这些干扰的存在使边界层流动变得复杂.为了研究边界层扰动波的演变,选取壁面沿流向观测点以记录扰动变量的时间演变过程,本文记录并分析了不同壁面观测点压力扰动的变化时间序列.图8给出了8个不同壁面位置的观测点压力扰动P'(x,y,t)随时间变化曲线.钝楔体表面母线S与x轴的关系如式(12)所示.
在壁面位置S=0.581 46处,即头部区域的压力扰动图(图8a)可以看出,由于头部正激波(近似正激波)的缘故,来流压力扰动通过激波后被显著地放大,随着时间的变化,经历增大—变小—再增大—再变小的振荡后消失为0.
图8b、图8c中矩形放大区域显示壁面压力扰动P'(x,y,t)小的振荡,这是因为反射波干扰引起的.

图8 不同壁面位置的压力扰动P'(x,y,t)

利用傅里叶变换对压力扰动的信号进行分解,并按频率顺序展开,使其成为频率的函数,从而将压力扰动的时域信号转化为频域信号,傅里叶变换如式(13)所示.
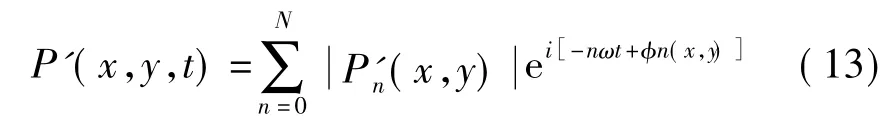
图9为不同壁面位置的压力扰动傅里叶变换后的幅值-频率图.图9显示:
1) 当S=0.581 46,即 S<π/2的球头区,壁面的压力扰动的傅里叶频谱分析(FFSA)幅值要远大于其他壁面位置的压力扰动的FFAS幅值;当在S>π/2的远离球头区,FFSA最大幅值首先迅速变小,之后保持基本不变.图8和图9均表明,扰动波在球头区(S<π/2)有很大的幅值,这正是球头前缘的正激波(近似正激波)放大了外加的扰动,且这些扰动在进入激波层后,在壁面和球头前缘的正激波(近似正激波)之间往复振荡,被放大[21],出了球头区,由于正激波迅速变为斜激波而使这种放大作用显著减弱.
2)S=0.58146 ~2.80255,低频迅速衰减,主导模态迅速向高频迁移,当S>2.802 55,主导模态在0.45<f<0.6(无量纲)频率段附近并缓慢地向高频迁移,在整个边界层发展阶段,主导模态是一个连续的频率波段,而不是间断的多个频率段.当 S<1.705 65,f<0.4 的低频扰动模态幅值要大于f>0.4的高频扰动幅值,低频波主导了边界层内扰动,但当S=1.70565 ~2.80255 时,总扰动模态中的低频模态(f=0.4以下)成分和高频模态(f=0.4以上)成分所占的比例开始转变,高频模态成分显著地增大,发展至S=3.83551处,f=0.5左右的扰动模态成为主导模态.并且随着边界层扰动模态沿流线的演变,频带明显向f=0.5(二阶谐频)附近收窄.
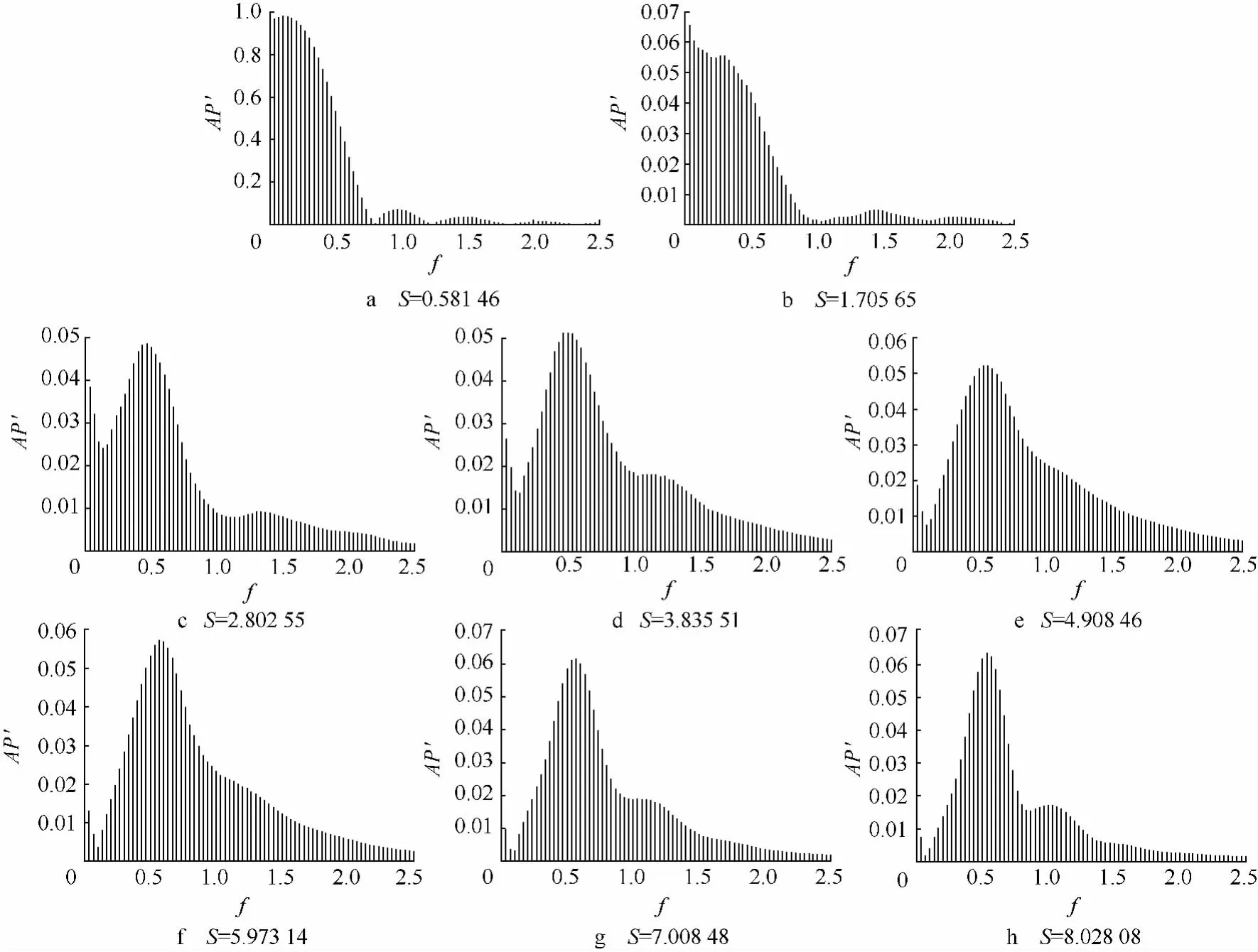
图9 不同壁面位置压力扰动傅里叶频谱分析幅值-频率图
3)在边界层内的发展阶段,一些扰动模态持续增长,一些扰动模态衰减,甚至被过滤掉,而也有一些扰动模态先衰减再增长.
图10为自由流脉冲波作用下钝楔边界层内不同压力扰动模态(基频波P1、谐波P2~P4)的幅值随S的变化.可以看到,无论基频波还是谐波,头部区域边界层的扰动模远大于远离头部区域的模.在钝楔头部区域基频扰动波的模远大于谐波,这表明头部区域边界层感受到的主要是基频波,这与文献[19]研究连续波情形得到的结果一致.出了球头区,边界层基频波保持基本稳定,而对于所有谐频模态,在初始阶段边界层都会迅速增长,而随着往下游流场的发展,除了二阶谐频模态持续增长外,其他模态受到抑制,要么不再增长保持稳定,要么迅速衰减基本被过滤掉.表明边界层存在扰动模态竞争的物理现象,主导模态的发展对其他模态的发展有很强的抑制作用.扰动幅值越大,扰动能量越大,这同时表明不同模态之间激烈的模态竞争伴随着能量迁移.
在诸多边界层对自由流或者壁面扰动的感受性研究中,线性稳定理论(LST)被引入分析该问题[21,23-24].即以定常流场的数值模拟结果作为平均流的解,在平行流的假设下,流动的扰动参数可写为正模态形式[21].对于空间模式,α = αr+ αi,αr为流向波数,αi为扰动波的增长率.图11a给出了自由流脉冲波作用下钝楔边界层内不同位置扰动波增长率随频率的变化.图11b给出了Xian等[21]、Zhong 等[23]、Malik 等[24]采用 LST 得到的自由流连续波作用下马赫数为7.99的来流绕7°半楔角钝体边界层扰动波增长率随频率的变化.由图11a和图11b可以看到,虽然两种情况下都存在不同频率扰动模态消与长的过程,但自由流连续扰动与脉冲扰动作用下,边界层扰动波的增长率变化与连续波情形显著不同.显然,一方面,这与扰动波的形式直接相关,另一方面,在基于空间模式扰动波增长率的分析中,自由流连续波情形,一般都是对处于时间周期状态的分析[14],即时域不相关;而自由流脉冲波情形,没有时间周期状态,即基于空间模式的边界层扰动波增长分析中同时存在时域演变.由图11a也可以看到,在流场上游(S<2.802 55),高阶谐频增长很快,特别是三阶谐频附近扰动模态增长最快,至下游流场(S>7.008 48),除二阶谐频附近模态持续增长外,其他模态迅速衰减,特别是三阶谐频附近衰减最为迅速,这将必然导致边界层扰动波频带向二阶谐频附近收窄,这些与图9和图10所得结果相符.
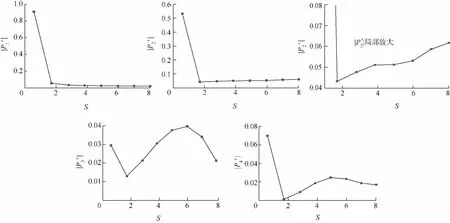
图10 边界层不同频率模态沿流向的压力扰动Pn幅值

图11 边界层扰动波增长率随频率变化
4 结论
本文采用高精度差分方法模拟了高超音速来流慢声波脉冲扰动非定常流场,分析了脉冲波与高超音速流场干扰,讨论了边界层扰动模态的发展,研究了脉冲波作用下高超音速边界层感受性特征.得出以下结论:
1)慢声波脉冲扰动波与弓形激波存在强烈的相互作用,弓形激波在来流慢声波脉冲作用下出现弯曲,自由流扰动波与激波干扰后产生强扰动波,流场气动特性被显著地影响,边界层外流场密度、温度将会产生斜条形奇异区.边界层内存在脉冲波、反射波与边界层之间复杂的相互干扰,边界层内外扰动波模态有显著差别.
2)在球头向非球头区过渡段,主导模态迅速向高频,特别是二阶谐频迁移,在远离球头区间,主导模态频率缓慢向高频迁移,总的来说,在球头附近f=0.4以下的低频扰动模态为主导模态.出了球头区,总扰动模态中的低频模态成分和高频模态成分所占的比例迅速转变,高频模态,特别是二阶谐频附近模态成分显著地增大.扰动波在边界层内的发展过程中,不同频率扰动模态呈现不同变化规律,但边界层不稳定扰动模态是一个连续的频率波段,而不是间断的多个频率段,沿流线发展,频带向二阶谐频附近明显收窄.
3)在球头区,所有模态迅速衰减,在非球头区上游流场(S<2.802 55),基频模态基本稳定,高阶谐频增长很快,特别是三阶谐频附近扰动模态增长最快,至下游流场(S>7.008 48),除二阶谐频附近模态持续增长外,其他模态迅速衰减,特别是三阶谐频附近衰减最为迅速.钝楔头部区域边界层感受到的主要是基频波,边界层不同扰动模态之间存在模态竞争的物理现象,主导模态的发展对其他模态的发展有抑制作用.不同扰动模态之间的模态竞争伴随着能量迁移.
References)
[1]Meyer B,Nelson H F,Riggins D.Hypersonic drag and heattransfer reduction using a forward-facing jet[J].Journal of Aircraft,2001,38(4):680 -686
[2]Hayashi K,Aso S.A study on reduction of aerodynamic heating by opposing jet in supersonic flow[J].Journal of the Japan Society for Aeronautical and Space Sciences,2004,52:38 -44
[3]Venukumar B,Jagadeesh G,Reddy P J K.Counter flow drag reduction by supersonic jet for a blunt body in hypersonic flow[J].Physics of Fluids,2006,18(11):571 -576
[4]Finley P J.The flow of a jet from a body opposing a supersonic free stream[J].Journal of Fluid Mechanics,1966,26:337 -368
[5]孙忠恕,温功碧.运动突风作用下机翼-机身-尾翼亚音速非定常气动力数值计算[J].航空学报,1981,2(3):23 -30
Sun Zhongshu,Wen Gongbi.Numerical computation of unsteady subsonic aerodynamic forces on wing-body-tail exposed to traveling gust[J].Acta Aeronautica et Astronautica Sinica,1981,2(3):23-30(in Chinese)
[6]王振清,唐小军,孟祥男,等.钝锥高超音速绕流脉冲扰动研究[J].哈尔滨工程大学学报,2013,34(3):298 -305
Wang Zhenqing,Tang Xiaojun,Meng Xiangnan,et al.Study on the effect of pulse perturbation in hypersonic flow over a blunt cone[J].Journal of Harbin Engineering University,2013,34(3):298-305(in Chinese)
[7]吴志刚,惠俊鹏,杨超.高超声速下翼面的热颤振工程分析[J].北京航空航天大学学报,2005,31(3):270 -273
Wu Zhigang,Hui Junpeng,Yang Chao.Hypersonic aerothermoelastic analysis of wings[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(3):270 - 273(in Chinese)
[8]Fedorov A V,Khokhlov A P.Receptivity of hypersonic boundary layer to wall disturbances[J].Theoretical and Computational Fluid Dynamics,2002,15:231 -254
[9]Malik M R,Lin R S,Sengupta R.Computation of hypersonic boundary-layer response to external disturbances[R].AIAA Paper 1999-0411,1999
[10]Maslov A A,Kudryavtsev A N,Mironov S G,et al.Numerical simulation of receptivity of a hypersonic boundary layer to acoustic disturbances[J].Journal of Applied Mechanics and Technical Physics,2007,48(3):368 -374
[11]Anatoli T,Wang X W,Zhong X L.Numerical simulation and theoretical analysis of perturbations in hypersonic boundary layers[J].AIAA Journal,2011,49(3):463 -471
[12]Wheaton B M,Juliano T J,Berridge D C,et al.Instability and transition measurements in the Mach-6 quiet tunnel[R].AIAA Paper 2009-3559,2009
[13]Saric W S,Reed H L,Kerschen E J.Boundary-layer receptivity to freestream disturbances[J].Annual Review of Fluid Mechanics,2002,34:291 -319
[14]梁贤.高超声速钝锥边界层稳定性特征[D].上海:上海大学,2009
Liang Xian.Boundary layer stability characteristics of hypersonic flow over a blunt cone[D].Shanghai:Shanghai University,2009(in Chinese)
[15]Kursat K,Ponnampalam B,Osama A K.Effects of nose bluntness on hypersonic boundary-layer receptivity and stability over cones[J].AIAA Journal,2011,49(12):2593 -2606
[16]Jiang G S,Shu C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics,1996,126:202-228
[17]Liu X D,Osher S,Chan T.Weighted essentially non-oscillatory schemes[J].Journal of Computational Physics,1994,115:200-212
[18]Lobb R K.Experimental measurement of shock detachment distance on spheres fired in air at hypervelocities[M].Washington:Defense Technical Information Center,1962
[19]Zhang Y D,Fu D X,Ma Y W,et al.Receptivity to free-stream disturbance waves for hypersonic flow over a blunt cone[J].Science in China Series G:Physics,Mechanics & Astronomy,2008,51(11):1682 -1690
[20]Prakash A,Parsons N,Wang X,et al.High-order shock-fitting methods for direct numerical simulation of hypersonic flow with chemical and thermal nonequilibrium[J].Journal of Computational Physics,2011,230(23):8474 -8507
[21]Liang X,Li X L,Fu D X,et al.Effects of wall temperature on boundary layer stability over a blunt cone at Mach 7.99[J].Computers& Fluids,2010,39(2):359 -371
[22]Kovasznay L S G.Turbulence in supersonic flow[J].Journal of the Aeronautical Sciences,1953,20(10):657 -682
[23]Zhong X L,Ma Y B.Boundary-layer receptivity of Mach 7.99 flow over a blunt cone to free-stream acoustic waves[J].Journal of Fluid Mechanics,2006,556:55 -103
[24]Malik M R.Prediction and control of transition in supersonic and hypersonic boundary layers[J].AIAA Journal,1998,27(11):1487-1493
