基于附加参数光束法平差的非量测型数码相机检校研究

曹良中，杨辽，李欣，张伟阁，贾洋，阚培涛

（1.中国科学院新疆生态与地理研究所，乌鲁木齐 830011；2.中国科学院大学，北京 100049；3.武汉大学 遥感信息工程学院，武汉 430079）

1 引 言

随着计算机技术、数字图像处理技术的进步，数字摄影测量已经逐步取代传统的解析摄影测量，成为当今摄影测量研究的主要测量方法，而数字摄影测量的一项重要任务就是获取原始影像。获取原始影像的装置可以分为两种：第1种是量测型相机，如DMC，UCX等。该类相机虽然内方位元素参数已知，影像几何位置关系明确，但是仪器笨重，价格昂贵，需要借助于大型飞机作为航摄平台，不能灵活机动的进行外业拍摄。第2种是非量测型相机，如单反相机，卡片机等［1］。该类相机具有价格低廉，体积小，重量轻，使用灵活方便，适应性强，社会拥有量大等优点。但毕竟不是专门为摄影测量而设计的，非量测型相机存在着镜头畸变差较大，内方位元素不稳定等缺陷。因此研究如何检校非量测型数码相机的畸变对于非量测型数码相机应用于生产，进而节省人力物力，提高经济效益具有重要意义。基于此，对相机检校方法的研究已成为近年来的研究热点。李平将直接线变换应用于相机检校［2］，该方法虽然能够覆盖所有像差变形，但是依靠直接线性变换求解通常只能独立处理单个模型，模型与模型之间不能整体平差［3］；张学民对两步法进行了改进并应用于相机检校［4］，该方法迭代参数少，能自动提供较好的初始值，求解速度快，考虑了部分像差，精度较高，但是像差修正只能是轴对称的，且对像主点无纠正［5］；谢文寒对基于多像灭点的相机标定进行了深入研究［6］，该标定方法操作简易、灵活，可做到“随时随地”标定相机，但是像主点对灭点误差的敏感度非常强，只能进行弱标定［7］。基于附加参数光束法平差的相机检校由于理论最为成熟、严密，因而检校的结果也最为精确，已广泛应用于非量测型数码相机的检校。

2 检校内容

相机检校的目的是为了恢复每张影像光束的正确形状，进而保证像点、对应的地面点以及投影中心位于一条直线上，因而对于数码相机而言，恢复每张影像光束的正确形状，需要检校的内容包括［8］：

①内方位元素：像主点位置（x0，y0）及主距（f）

②光学畸变差：径向畸变，偏心畸变

2.1 内方位元素

内方位元素是用来确定相机的镜头中心相对于影像位置关系的参数，它包括以下3个参数：像主点相对于影像中心的位置x0，y0以及镜头中心到影像面的垂距f。当这3个参数获取之后，摄影光束的形状即可确定。

2.2 光学畸变差

光学畸变差是指相机物镜系统在设计、制作以及装配阶段所引起的像点偏离其理想位置的点位误差。作为影响像点坐标质量的一项重要误差，光学畸变分为径向畸变和偏心畸变［9］。

2.2.1 径向畸变

径向畸变是指像点沿物镜向径方向偏离其准确理想位置的畸变差，由镜头形状缺陷所引起，它只与像点离主点的距离有关。一般径向畸变差是对称的，对称中心与主点并不完全重合，但通常将主点视为对称中心，径向畸变有正有负，相对主点向外偏移为正即桶形畸变，向内偏移为负即枕形畸变。图1中的a、b、c分别为径向畸变中的桶形畸变、枕形畸变和无畸变3种情况。

图1 径向畸变

根据几何光学原理，物镜的径向畸变可用公式（1）表达：

其中，Ki是径向畸变系数；r为径向距离。

2.2.2 偏心畸变

偏心畸变是由于装配和振动使得物镜系统各单元透镜偏离了轴线或歪斜，从而引起像点偏离其准确理想位置的畸变。

根据几何光学原理，物镜的偏心畸变可用公式（2）表达：

其中：Pi是偏心畸变系数。

一般情况下，偏心畸变远比径向畸变小，仅为径向畸变差的1／5～1／7，对于较好的物镜系统，偏心畸变差影响就更小［10］。

3 检校的原理

本文采用附加参数光束法平差测定内方位元素和光学畸变差。它是由共线条件方程式演绎而来，其基本关系式如（3）［11］：

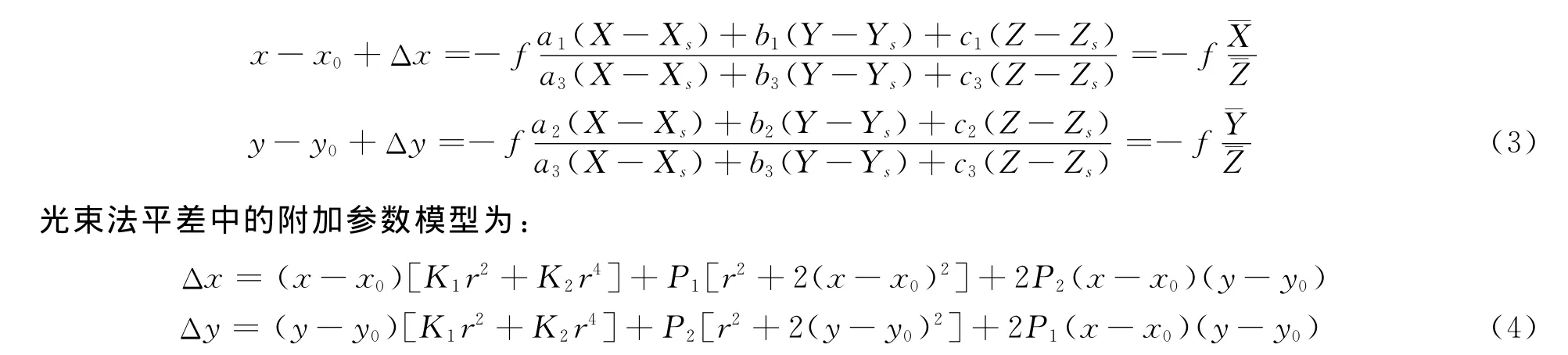
其中，（x，y）为像点坐标，（x0，y0）为像主点坐标，（X，Y，Z）为地面点坐标，（Xs，Ys，Zs）为摄影中心相对物方坐标系的位置，Ki为径向畸变系数，Pi为偏心畸变系数，r为径向距离。

将控制点坐标视为真值，像点坐标视为观测值，各项畸变系数和待定点的空间坐标视为未知数，附加参数的光束法平差的误差方程如公式（5）所示。

设X1，X2，X3，X4分别为外方位元素改正数、内方位元素改正数、待定点坐标改正数、为系统畸变系数改正数。设A1，A2，A3，A4为相应未知数的系数向量，L＝ ［x－（x）y－（y）］T，其中，（x），（y）为按共线方程计算的各片像点坐标近似值，（x，y）为像点量测坐标，则误差方程如式（6）所示。

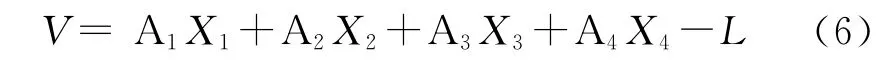
根据误差方程即可列出相应的法方程，进而解算出内方位元素以及相机畸变参数。

4 相机检校

4.1 相机介绍

此次试验采用的相机为PhaseOne IQ180－645DF中幅面数码相机，此相机的相关参数见表1。

表1 待检校相机参数

4.2 相机固定

由于待检校相机为非量测型相机，其部件间的连接存在着微小的隙动且没有任何加固措施，如果不做任何处理，会影响相机稳定性，同时也会影响相机调焦位置的固定。因此，通过机械加固对相机进行了固定，以保证检校结果的持续可用性。

4.3 检校场拍摄

应用待检校的数码相机对武汉大学高精度室内三维实验场进行了数据采集。为了避免数码相机结构上的不严谨所造成的焦距变化和主点位置（x0，y0）变化，并为了保证每张影像上主距f相同，在拍摄时将摄影方式设为手动曝光方式。为了锁定主距（锁定主距之后内方位元素值和物镜畸变系数保持不变），本文将物镜的焦距固定在无穷远处。另外，通过相机绕光轴旋转90°获取2张旋转影像，目的是削弱像主点、主距和畸变差的相关性等，进一步提高标定精度。在控制场内，分别在6个摄站对室内高精度三维控制场拍摄6张影像，其中2张旋转90°摄影，平均摄影距离5m。

图2 检校用影像

4.4 相机检校

本次相机检校采用自己编写的检校软件进行检校，该软件由面向对象程序设计语言Visual C＋＋编制，主要由以下3个功能模块构成：标志点像平面坐标的自动识别获取模块，基于附加参数光束法平差的成果计算模块和计算结果精度分析模块。图3为软件设计流程图。

采用光束法平差计算时，在控制场中选取9个点作为检查点，其物方空间坐标与检校参数同时计算。经过计算，检校参数结果如表2所示。

图3 软件设计流程图

表2 检校结果

5 精度分析与可靠性验证

5.1 精度分析

经过计算，观测值单位权中误差σ＝±0.29976pixel，各检校参数精度统计如表3、表5所示（注：Y方向为摄影方向）。

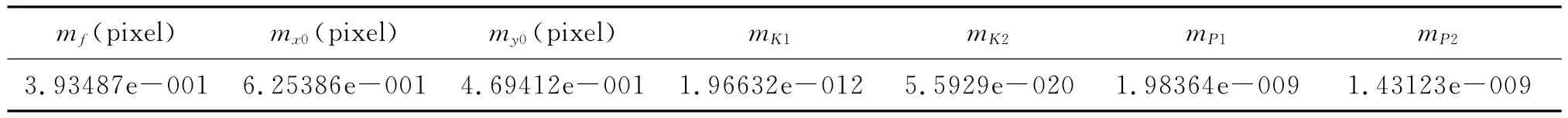
表3 内方位元素及畸变系数精度

表4 各影像外方位元素精度

表5 检查点精度

图4 试验区概略图

5.2 可靠性验证

前面对检校参数的分析，只是从检校参数精度方面说明了应用基于附加参数光束法平差的这种检校方法所检校出的各参数结果满足规定要求，但不能真实说明各检校参数实际的可靠程度。为了真实地反映检校成果是否真正可靠，在新疆和静县采用该相机进行了一次可靠性验证试验。试验区位于86°22′7.08″E～86°24′51.97″E，42°18′3.64″N～42°20′9.64″N，试验区面积为15.9927km2。该次试验飞行参数如表6所示。

表6 飞行参数

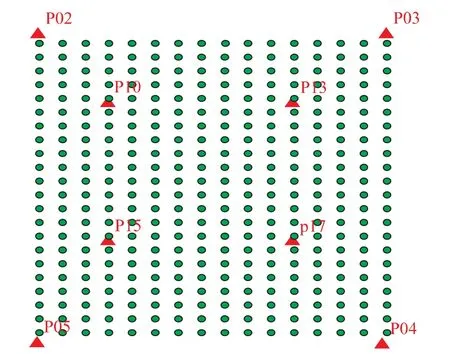
图5 检查点分布情况

为了对比检校好的相机参数对精度的影响，分别用原始相机参数和检校后的相机参数做了两次空中三角测量，为了避免刺点对两次实验的结果产生影响，控制点只刺1次，第2次空三直接导入第1次选刺的结果。经过试验，检校前和检校后控制点精度表7所示。

表7 检校前后检查点精度对比

表7中精度已经基本上满足测制1∶500等大比例尺地形图的要求，进一步验证了相机检校参数的可靠性。

6 结束语

本文运用附加参数的光束法平差方法对PhaseOne IQ180－645DF相机进行了检校，通过对检校的结果和可靠性分析表明：应用附加参数的光束法平差方法检校出的各参数结果可靠，经过检校的相机，其采集的影像数据经过影像改正后可以满足摄影测量的应用要求，能够应用于大比例尺测图，此方法可以推广到其他数码相机的检校。

［1］杨军.非量测数码相机检校方法的研究［J］.测绘科学，2009，34（4）：89－91.

［2］李平.非量测型数码相机检校［D］.西安：西安科技大学，2009.

［3］苗红杰.数码相机应用于物体表面三维重建的检校技术研究［D］.北京：首都师范大学，2005.

［4］张学民，宋述隐.两步法摄像机标定的改进［J］.自动测量与控制，2006，25（9）：73－75.

［5］苗红杰，赵文吉，刘先林.数码相机检校和摄像测量的部分问题探讨［J］.首都师范大学学报（自然科学版），2005，20（1）：117－120.

［6］谢文寒.基于多像灭点进行相机标定的方法研究［D］.武汉：武汉大学，2004.

［7］詹总谦.基于纯平液晶显示器的相机标定方法与应用研究［D］.武汉：武汉大学，2006.

［8］王冬，冯文灏，卢秀山.NikonD1X相机检校［J］.测绘科学，2007，32（2）：33－35.

［9］张本昀，吴晓明，喻铮铮，等.非量测型相机检校及可靠性研究［J］.测绘科学，2008，33（10）：84－86.

［10］陈新玺，李浩，张曼祺.普通数码相机构像畸变差两种检校模型的比较［J］.北京测绘，2005（4）：51－54.

［11］冯文灏.近景摄影测量［M］.武汉：武汉大学出版社，2002.