大型集装箱船弹振和颤振研究

吴 小 平

（上海船舶研究设计院，上海 201203）

式中： jp——第j个海况出现的概率； jFDR——第j个海况对结构造成的疲劳损伤率。分别计算各个装载工况下的疲劳损伤率，根据船舶生命期内各装载工况所占的航行时间比例，即可得到船舶的疲劳损伤。例如船舶设计寿命25年，满载和压载比例分别为 sP和 bP，以迎浪为例，疲劳损伤为：

0 引 言

近年来，集装箱船的大型化趋势非常明显。集装箱船越大，其单位装箱的运费就越低。与此同时，集装箱船的巨型化给结构设计提出了更高的要求。大型集装箱船的结构设计不能仅将适用于中小型集装箱船的规范进行简单的外延，而应更多地考虑船体巨型化所带来的一系列非线性影响，例如砰击、弹振和颤振等，本文将主要研究弹振和颤振对大型集装箱船的影响。

为了在甲板上装载尽可能多的集装箱，集装箱船一般都具有大外飘的特点，大型集装箱船尤为明显。过大的艏外飘，直接导致其艏部容易受到波浪砰击作用。砰击不仅会造成局部结构破坏，而且还有可能引起船体梁振动，给总强度带来危害。相对中小型集装箱船而言，大型集装箱船刚度较小，固有频率较低；另一方面，大型集装箱船航速快，在迎浪航行时遭遇频率会随着航速的增加而增大，当船体梁的垂向2节点固有频率与波浪遭遇频率接近时，船体梁将发生共振，称为弹振；当船体梁受到瞬间剧烈的砰击作用时，船体梁会产生瞬间高频振动，称为颤振[1]。弹振和颤振对船体梁结构强度都会产生不利影响，弹振主要影响船体梁的疲劳强度，而颤振则更多地体现在对极限强度的影响。事实上，弹振和颤振往往同时发生，二者之间并无明显的区分界限。

1 船舶运动

弹振和颤振本质上是船舶在波浪中的一种振动行为，与船舶在波浪中的相对运动有关。为了了解船舶在波浪中的运动情况，首先要对其进行耐波性分析。目前可采用的数值分析方法有频域方法和时域方法。前者用于对波浪进行大规模筛选，获取频域响应函数；后者用于对筛选出的危险海况作进一步分析。频域方法中，通常在迎浪和随浪之间，以15°为间隔，选取多个浪向。对于每个浪向，选取20～30个波浪频率，进行相对运动和相对速度的响应计算。通过计算得到频域响应函数，由频域响应函数和波浪谱确定响应谱：

式中：SR（ω）——响应谱密度函数；Sξ（ω）——波浪谱密度函数； H（ω）——频域响应函数。由响应谱可得到短期响应统计值，对于第j个海况，响应值超过 x0的短期概率 P rj为：

式中：0jm ——响应谱零阶谱矩。短期响应预报一般只适用于数小时之内的短期海况，而要计算船舶在生命期内的长期响应值，则要进行长期响应预报。响应值超过0x的长期概率Pr为：

式中：ip、jp——为第i个浪向和第j个海况出现的概率，通常取10–8超越概率水平作为长期设计极值。根据长期响应极值和频域响应函数，可以推导出用于时域分析的等效设计波。对于任意主要控制参数，其等效设计波波幅wa为：

式中：LTR——长期响应极值；RAOmax——频域响应函数的最大值。等效设计波的频率和浪向为 R AOmax对应的频率和浪向。

2 砰击

砰击是指船体某处出水后，由于相对运动又迅速浸没于水中，导致船体与波浪之间发生剧烈相互作用的一种现象。砰击由波浪引起，船体和波浪之间的垂向相对运动将直接决定砰击是否发生以及砰击的剧烈程度。砰击可分为三种：底部砰击、艏外飘砰击、艉部砰击[2]。对于集装箱船，由于其明显的艏外飘和方艉特点，将重点考虑艏外飘砰击和艉部砰击。图1所示为艏外飘砰击计算点。大量研究表明，发生砰击必须具备两个条件：一是垂向相对位移要超过局部吃水，二是垂向相对速度要超过某一临界速度。该临界速度可表示为船长的函数[3]：

图1 艏外飘砰击计算参考点

式中：Vcr——临界速度，m/s；g——重力加速度，m/s2；L——船长，m。根据发生砰击的两个条件在统计上不相关的事实，砰击概率可表示为两个条件概率的乘积[3]：

艏部出水概率为：

相对速度超过临界速度的概率为：

式中：rη和rV——相对位移和相对速度；和——相对位移和相对速度的方差；d——参考点到水线的垂向距离。将式（7）和式（8）代入式（6），则砰击概率可表示为：

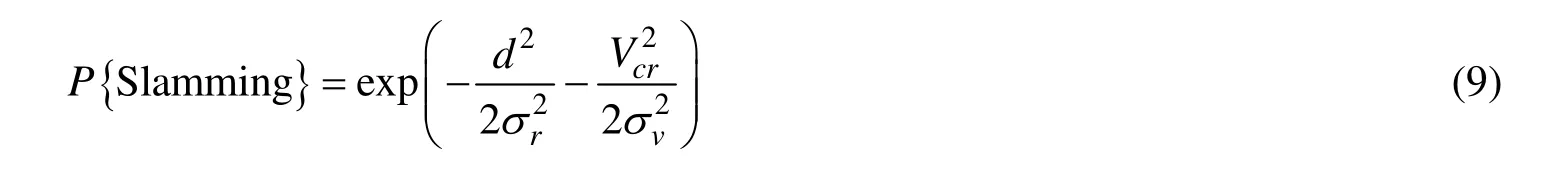
3 弹振和颤振的简化算法

3.1 冲击载荷

冲击载荷与艏部的形状和相对运动速度有关。对于大型集装箱船，可以将其水线以上、计算参考点以下的艏部横剖面近似看作楔形，其单位长度的冲击载荷可表示为[4]：

式中：q——冲击载荷，kN；ρ——水密度，t/m3；rV——相对运动速度，m/s；t——时间，s；pC ——砰击系数，可近似表示为斜升角α的函数并参见图2。

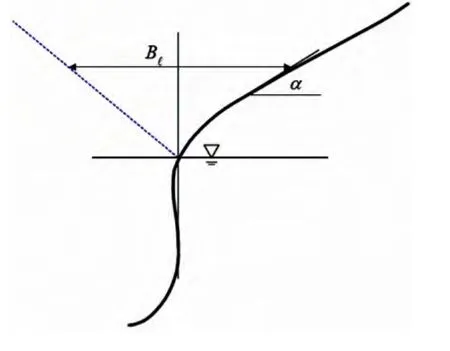
图2 砰击系数计算

3.2 弹振对疲劳损伤的影响

对于刚体船体运动分析，波浪频率一般取0.2～1.2rad/s即可，如果考虑水弹性，波浪频率范围应扩大到至少能覆盖2节点垂向振动固有频率，建议取0.2～10.0rad/s。疲劳损伤表达式为[5]：

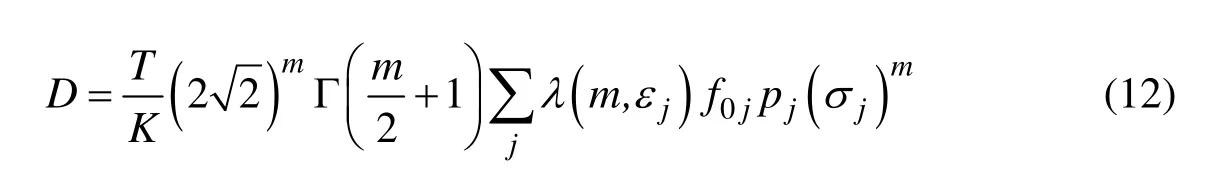
式中：D——疲劳损伤；m、K——S–N曲线参数；T——疲劳设计年限；pj——第j个海况出现的概率；σj——该海况作用下的应力幅值范围；f0j——应力响应的过零频率；Γ(⋅)——完整Gamma函数；λ(⋅)——带宽修正系数；εj——带宽参数。

如果不考虑弹振的影响，则疲劳损伤可认为完全由波浪引起，其疲劳损伤可由式（12）直接计算，记为 Dwave。如果考虑弹振影响，则疲劳损伤由波浪和弹振共同引起，为了对二者进行区分，此时应将响应谱在某一频率处分为两个区间，分别代表波浪和弹振对疲劳损伤的作用区间。对于大型集装箱船，这一频率可取 2.0rad/s。对响应谱的两个频率区间分别进行统计分析，得到波浪和弹振的响应方差、响应过零频率等。计算波浪和弹振引起的总疲劳损伤，记为 Dtotal_s。于是可得到弹振对疲劳损伤的影响程度，以系数αs表示[5]：

3.3 颤振弯矩

根据冲击压力，计算由颤振引起的垂向弯矩[4]：

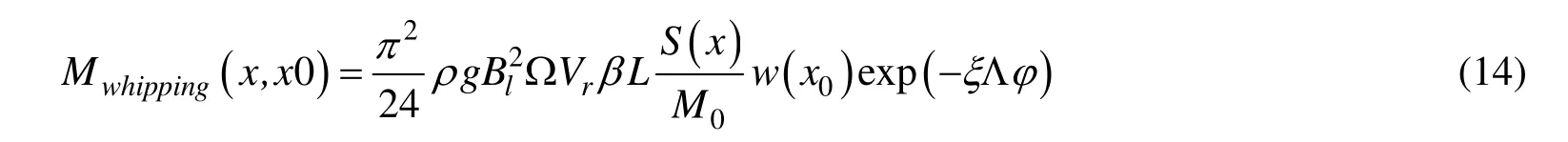
式中：Ω——2节点振动固有频率，rad/s；ξ——2节点振动模态阻尼系数，可近似取1.5%，Λ=Tz/T2，其中 T2——2节点振动固有周期，s；Tz——海况过零周期，s；φ——颤振弯矩与波浪弯矩的相位差，可取 30°。

3.4 颤振对疲劳损伤的影响

由颤振和波浪引起的总疲劳损伤可以近似分为两部分：一部分由颤振单独引起，另一部分由波浪响应和颤振响应的包络部分引起。前者引起的疲劳损伤为[4]：

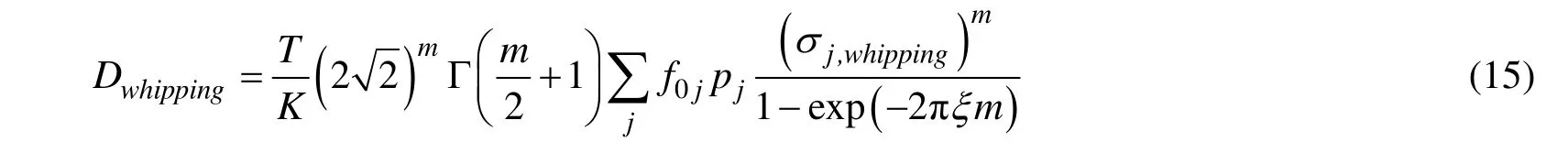
包络部分的疲劳损伤为[4]：

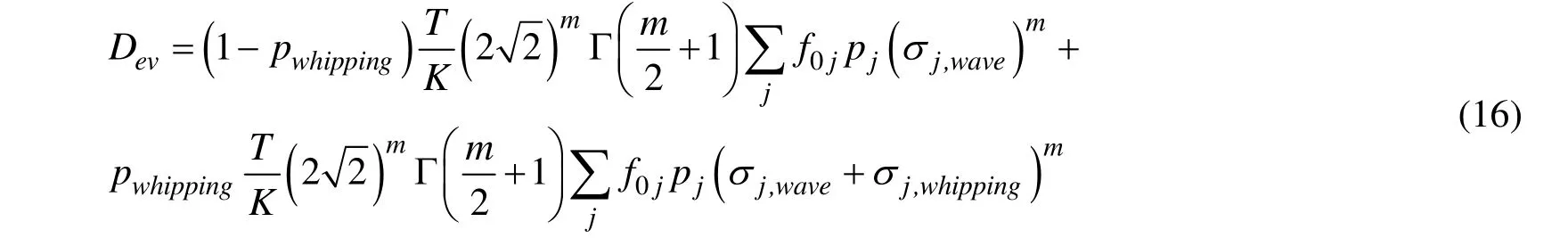
式中：pwhipping——颤振概率。计算波浪和颤振引起的总疲劳损伤，记为Dtotal_w。

由此可知颤振对疲劳损伤的影响程度，以系数wα表示[4]：

4 试验研究

由于弹振和颤振涉及水弹性理论，目前这方面的研究正处于发展当中，常规数值分析方法尚无法取得令人满意的效果。要得到精确可靠的结果，应采用模型试验的方法。

4.1 试验设置

与阻力模型试验不同，用于弹振和颤振试验的模型采用多个分段连接而成，通过调节连接处的弹性铰接装置，可以实现模型刚度调节。模型的质量分布也可以调节。通过调节刚度和质量分布，使模型的固有频率与实船的固有频率相一致。

模型设置好之后，根据海况要求，在耐波性水池中制造规则波或不规则波，对模型进行试验，模型上的测量传感器记录测量数据，用于数据处理。

4.2 海况选择

根据实际航线选择合适的海况。理论上，最准确的方法是对波浪散布图中所有可能出现的海况进行试验，但工作量非常大。常用的做法是根据经验在波浪散布图中选择有代表性的海况，例如，选择4个波高、4个周期，对二者进行组合可得到16个海况，如表1所示[6]。

图3 弹振颤振试验模型[6]

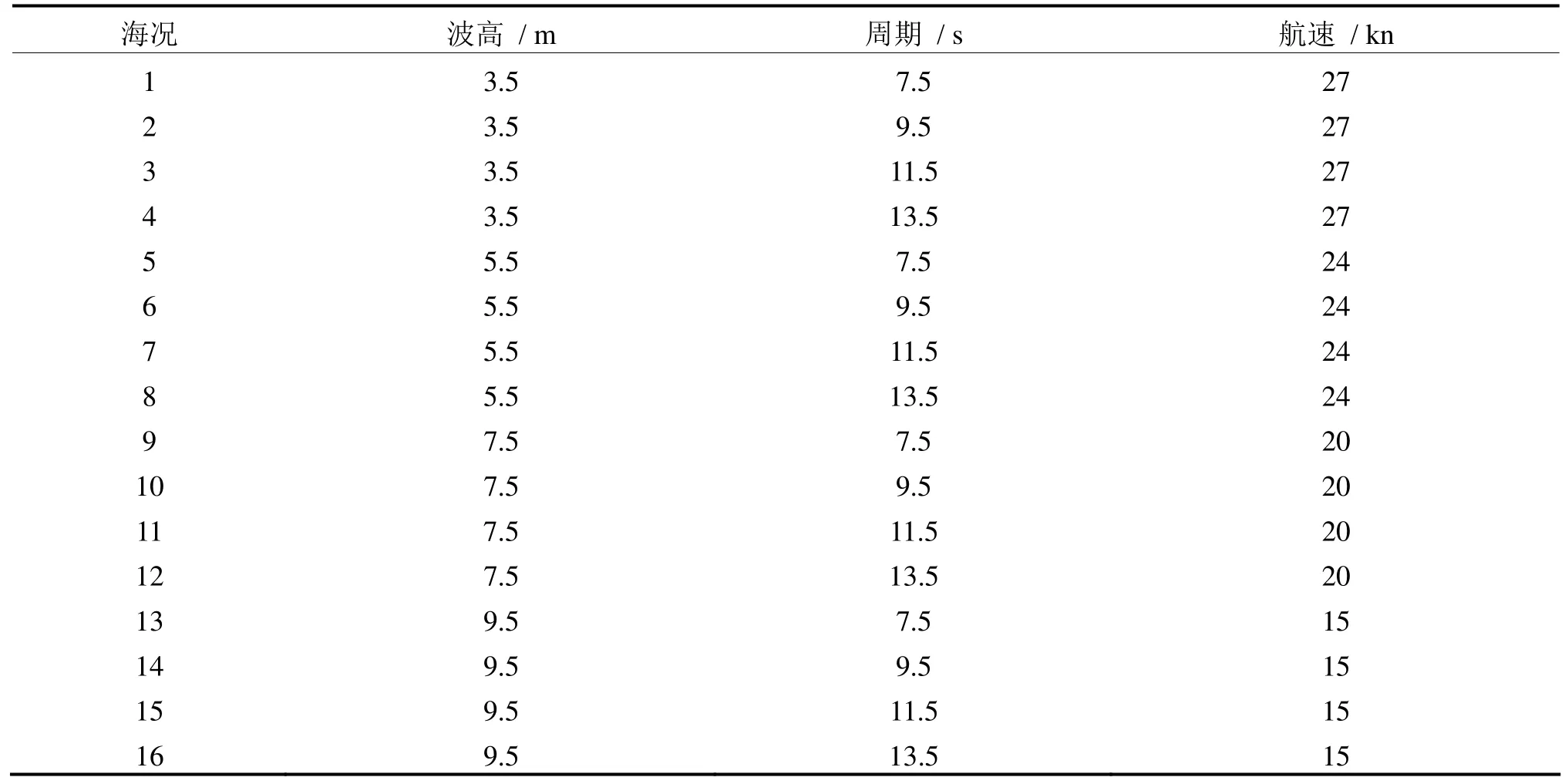
表1 海况选择

4.3 疲劳损伤

疲劳损伤的计算方法很多，最常见的是基于线性累积损伤理论的S–N疲劳曲线方法。这种方法的基本原理是将结构累积损伤表示为不同应力水平下的损伤之和[7]。

式中：D——累积疲劳损伤；ni——第i个应力范围中应力次数；Ni——根据应力范围Δσi由S–N曲线查到的次数；k——应力范围的个数；、m——S–N曲线疲劳参数，S–N曲线中各参数之间的关系如下：

对于迎浪航行状态，名义应力可近似表示为：

式中：σnorminal——名义应力；VBM——垂向弯矩；Z——计算参考点距基线高度；Zneutral——中性轴距基线高度； Iyy——计算剖面对y轴的惯性矩。

通过对某大型船舶进行弹振和颤振模型试验，结果表明，由于弹振和颤振的影响，垂向弯矩有明显增加。平均增加幅度为30%～50%，有些时刻甚至达到100%。这种瞬间冲击将会造成瞬间高应力，对船体梁的总强度带来极大考验。根据测量得到的垂向弯矩时域曲线，通过雨流计数法计算出时域信号的幅值范围，进而根据式错误！未找到引用源。得到应力的幅值范围。根据实际情况选择应力集中系数，得到切口应力幅值范围。选择适当的S–N曲线，即可由式（19）计算疲劳损伤。

4.4 疲劳损伤率

将计算得到的疲劳损伤除以试验时间，得到疲劳损伤率，即单位时间内的疲劳损伤。对表1中的每个海况，按照上述步骤进行试验和计算，得到每个海况的疲劳损伤率。根据海况在波浪散布图中出现的概率和疲劳损伤率，计算平均疲劳损伤率，见式（22）。

式中：jp——第j个海况出现的概率；jFDR——第j个海况对结构造成的疲劳损伤率。分别计算各个装载工况下的疲劳损伤率，根据船舶生命期内各装载工况所占的航行时间比例，即可得到船舶的疲劳损伤。例如船舶设计寿命25年，满载和压载比例分别为sP和bP，以迎浪为例，疲劳损伤为：

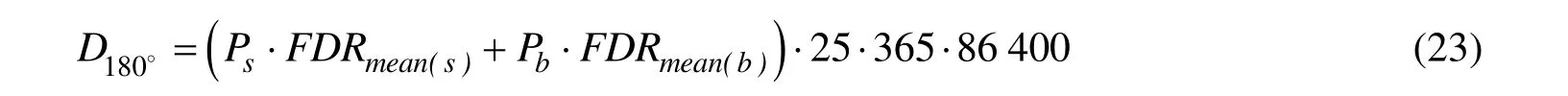
式中：FDRmean( s )、 FDRmean(b)——分别为满载和压载平均疲劳损伤率。

图4为某13000TEU超大型集装箱船弹振和颤振模型试验结果[6]，图中横坐标为海况编号（见表1），纵坐标为疲劳损伤率。从图4可以看出，多个海况下弹振和颤振引起的疲劳损伤要高于波浪引起的疲劳损伤。这表明，对于超大型集装箱船来说，弹振和颤振对船体结构的影响非常显著，如果忽略它们的影响，势必会带来安全隐患。从图4中还可以看出，随着波浪周期增加，弹振和颤振疲劳损伤有下降的趋势。这表明，波浪周期增加，频率降低，波浪频率远离船体梁2节点固有频率，所以对减小疲劳损伤有利。

4.5 弹振和颤振对疲劳的影响

分别计算有弹振颤振作用和无弹振颤振作用时的平均疲劳损伤率，比较二者可以发现弹振和颤振对船体疲劳损伤的影响。

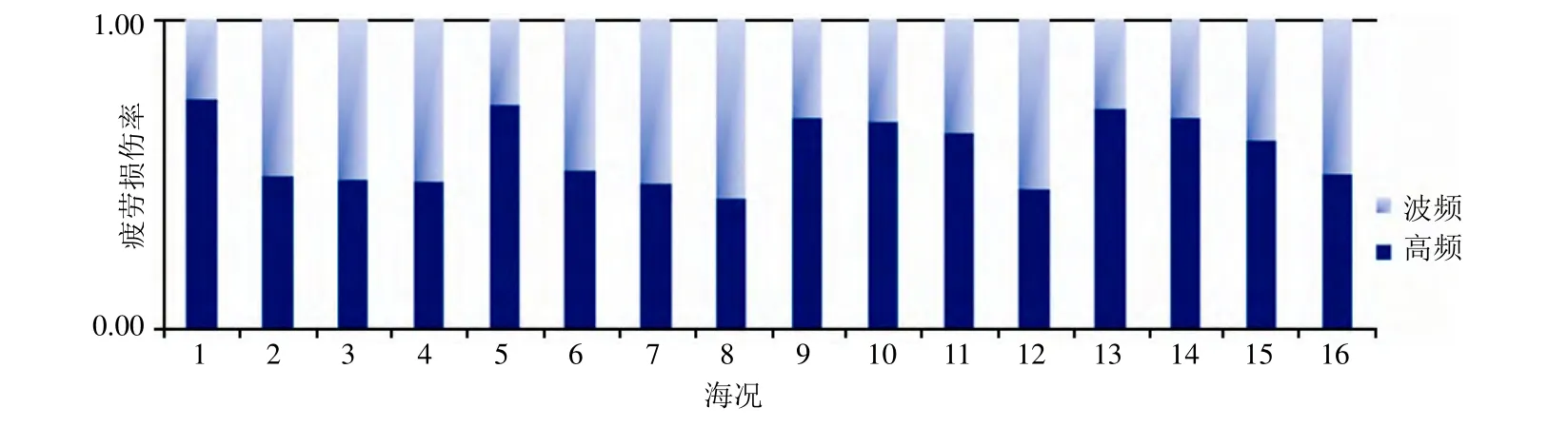
图4 疲劳损伤中波频和高频组成成分比较

5 结 语

由于具有刚度小、航速高的特点，大型集装箱船容易受到弹振和颤振的作用。研究表明，弹振和颤振对大型集装箱船的结构强度有重要影响，由于弹振和颤振，船体疲劳损伤和极限弯矩都有显著增加，在恶劣海况下，弹振和颤振对船体的影响甚至已经超过波浪对船体的影响，在设计中应予以关注。

[1] Storhaug, G. Experimental Investigation of Wave Induced Vibrations and Their Effect on the Fatigue Loading of Ships[D]. PhD dissertation, Norwegian University of Science and Technology (NTNU). 2007.

[2] American Bureau of Shipping. Guide for Slamming Loads and Strength Assessment for Vessels[S]. 2011.

[3] O.M. Faltinsen. Sea Loads on Ships and Offshore Structures[M]. Cambridge University Press. Cambridge. 1990.

[4] American Bureau of Shipping. Guidance Notes on Whipping Assessment for Container Carriers[S]. 2010.

[5] American Bureau of Shipping. Guidance Notes on Springing Assessment for Container Carriers[S]. 2010.

[6] Gaute Storhaug, Sime Malenica, etc. Consequence of Whipping and Springing on Fatigue and Extreme Loading for a 13000TEU Container Vessel based on Model Tests[OL]. http://www.veristar.com.

[7] MingKang Wu. Evaluation of Fatigue Damage Rates Based on Model Tests for the 400,000 DWT Ore Carrier Designed by Shanghai Merchant Ship Design and Research Institute[R]. Marintek report No. 530527.00.10. 2010.