一类双调和方程基态解的存在性

杨玉蓓

（武汉工程大学邮电与信息工程学院，湖北 武 汉430079）

0 引言

我们研究如下双调和方程：

的基态解的存在性．

在文献［1］中，Ambrosetti和Rabinowitz给出了山路引理，并且利用它得到了以下有界边值问题的基态解的存在性．此时，非线性项要求满足AR条件，即

（AR）存在μ＞2，使得0＜μF（x，u）≤uf（x，u），其中

在其后相关问题进行研究时，多半的非线性项赋予了AR条件，也得到了许多很好的结果．由AR条件，容易得出F（x，u）≥C｜u｜μ．自然而然地，我们不禁要问如果我们将方程（2）中非线性项的条件改成超二次增长，即

那么又会有什么样的结果呢？

我们注意到，验证山路引理的几何结构和PS序列的有界性都离不开AR条件，而在超二次条件（SQ）下，这些都是难以验证的．

文献［2］中，刘兆理，王志强利用Nehari流形方法来处理方程（2），得到了其基态解的存在性．文献［3］中，李永青，王志强，曾晶又将文献［2］中的结果推广到无界域．本文中，我们将文献［3］中的结果推广到双调和方程（1）．

我们的记号是标准的．C总是指正常数．→和⇀分别表示相应空间中的强收敛和弱收敛．2＊＝．m表示Rn上的勒贝格测度．

1 主要结果及其证明

我们考虑如下方程：

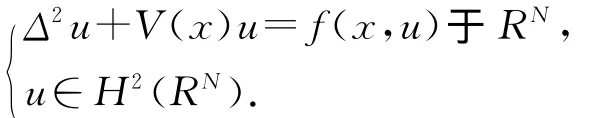
其中f（x，u），V（x）满足以下假设：

（V）V（x）∈C（RN，R），inNfV（x）≥V0＞0，V（x）对于自变量的每一分量x1，…，xN都以1为周期．

R

（f1）f（x，t）∈C1对于x的每一分量x，…，x都以1为周期．f是Caratheodory函数并且存在常

1Nt

数C＞0使得

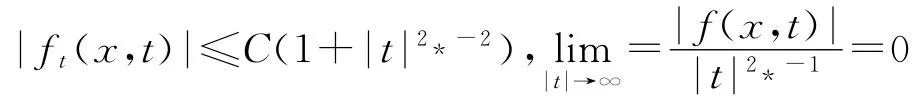
关于x∈RN一致成立．

（f2）f（x，t）＝o（t）（t→0）关于x∈RN一致成立．

方程（1）式的能量泛函是：

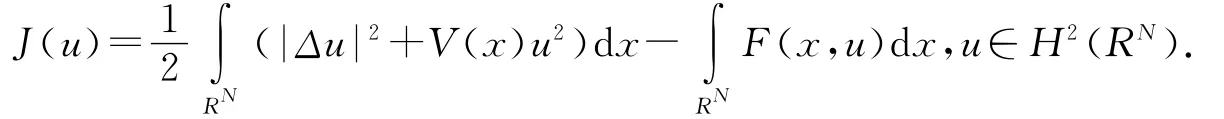
我们的主要结果是：

定理 在条件（V），（f1）～（f4）下，方程（1）式具有基态解．即存在w∈H2（RN）使得对于任何φ∈H2（RN）都有，并且，其中 N ＝｛u∈

在证明定理以前，我们先证明几个引理．

引理1．1的证明 参见文献［4］中的定理4．2．

引理1．2 令｛un｝⊂N是关于c的极小化序列，则

（ⅰ）∃β＞0，使得‖un‖H2≥β．

（ⅱ）｛un｝在 H2（RN）中有界．

（ⅲ）在抽取子列的意义下，∃yn∈ℕN，使得⇀u≠0于H2（RN），其中（x）＝un（x＋yn）．

引理1．2的证明 （ⅰ）由（f1），（f2）知，对于∀ε＞0使得，故

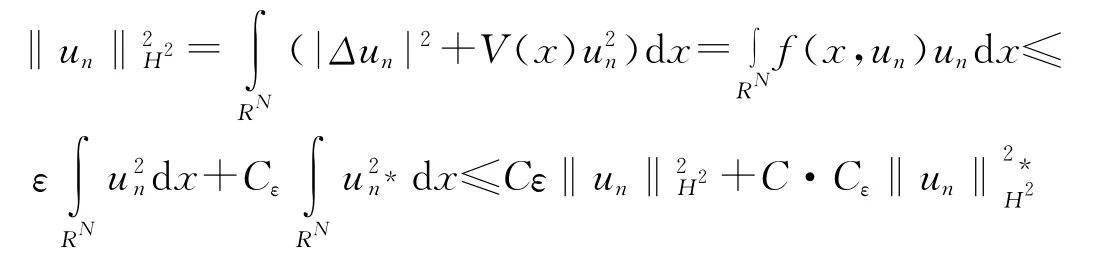
（ⅱ）如果｛un｝无界，我们定义vn＝un／‖un‖H2，则‖vn‖H2＝1．在抽取子列的意义下于H2（RN），对一切q∈［1，2＊），有

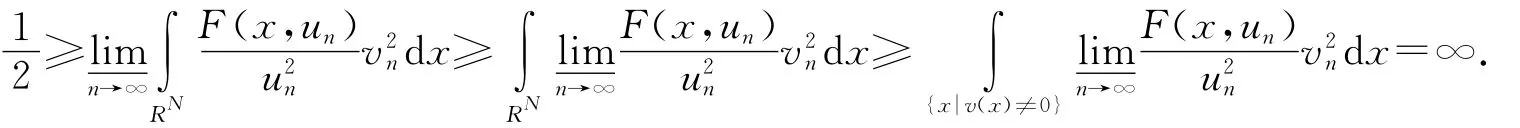
得到矛盾．

v′a．e．如果存在yn∈ℕN使得，类似于前述v≠0的情形，可以得到矛盾．

由消失引理（见参考文献［5］），对任何q∈（2，2＊），vn→0于Lq（RN）．固定s∈（2，2＊），由（f1），（f2），对于∀ε＞0，∃Cε＞0使得则，固定有

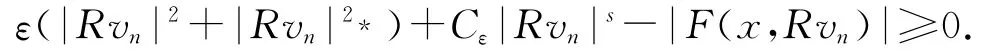
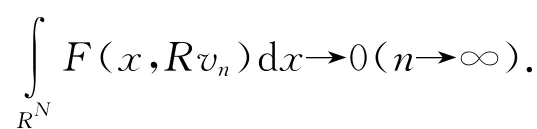
再由Fatou引理可知

由（f4），对一切t＞0，有J（tun）≤J（un），故

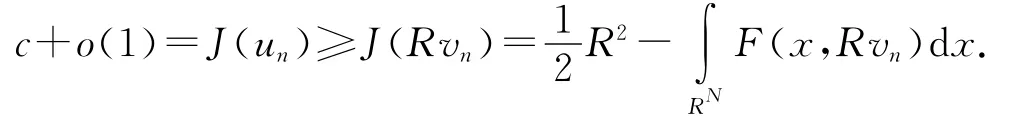
令n→∞，可得矛盾，故｛un｝在 H2（RN）中有界．

（ⅲ）若对于一切yn∈ℕN，都有⇀0于H2（RN），类似于（ⅱ）的证明，我们有对任何q∈（2，2＊），，结 合 （f1），（f2）可 知 当 n→ ∞ 时 ，．再结合（ⅰ）有0＜β2≤，矛盾，（ⅲ）成立．

引理1．3 任取u∈H2（RN）＼＼｛0｝，存在唯一的t（u）＞0，使得t（u）u∈N．

引理1．3的证明 参见文献［6］．

引理1．4 令｛un｝⊂H2（RN）满足，则存在tn＞0，使得，并且当n→∞时，tn→1．

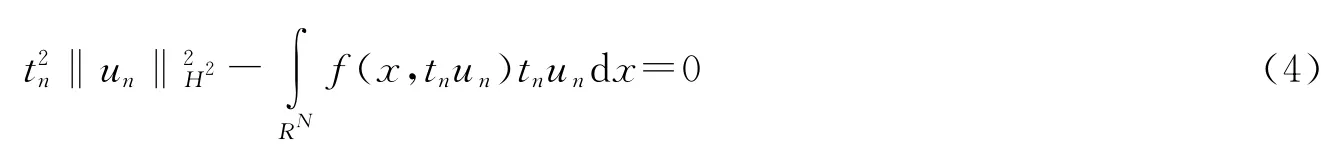
由（f1），（f2），对于∀ε＞0，∃Cε＞0使得｜f（x，u）u｜≤ε｜u｜2＋Cε｜u｜2，故

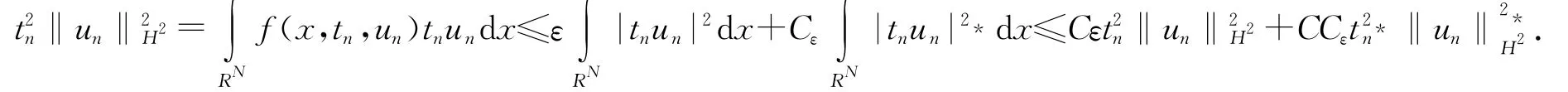
则

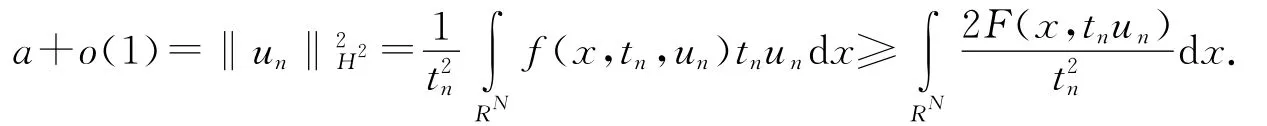
类似于引理1．2，在相差一个平移的意义下，un→u＝0a．e．故由（f3）可知

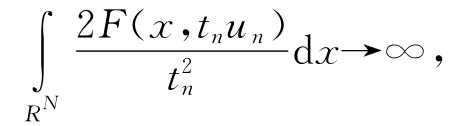
矛盾．故tn有正下界正上界，设tn→T＞0．由〈J′（un），un〉→0，知

将方程（1）式限制在开球BR（0）上，即考虑如下方程

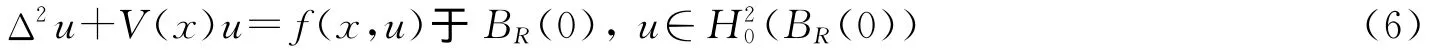
方程（6）式的能量泛函是：

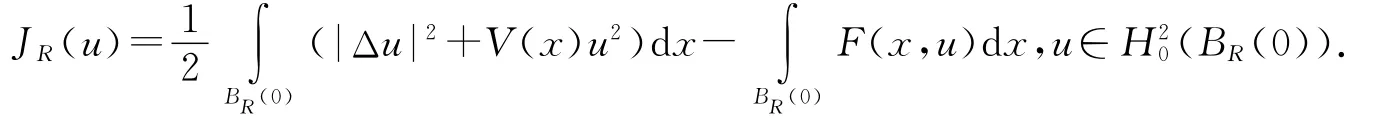
引理1．5 方程（6）式具有基态解．

引理1．5的证明 令｛wn｝⊂NR是cR的极小化序列，类似于引理1．2（ⅱ）的证明，可知｛wn｝在（BR（0））中有界．故不妨假设wn⇀wR于H20（BR（0））．类似于1．2（ⅰ），有，则

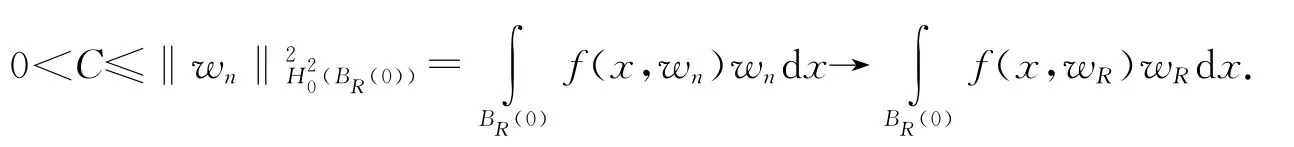
故wR≠0，存在tR＞0，使得tRwR∈NR，故

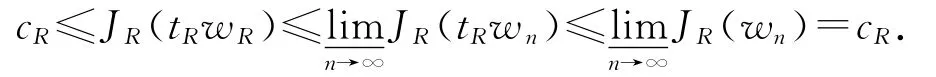
记tRwR＝uR，由拉格朗日乘子定理，∃λ使得J′R（uR）＝λγ′R（uR），其中γR（·）＝〈J′R（·），·〉由（f4），〈γ′R（uR），uR〉＜0．由于tRwR∈NR，〈J′R（uR），uR〉＝0．故λ＝0．则λ′R（uR）＝0，即uR是（6）式的基态解．

容易验证cR≥c，并且当R→∞时，cR→c，这说明｛uR｝是c的极小化序列．令Rn→∞，记un∶＝uRn，固定s∈（2，2＊），有

引理1．6 在抽取子列的意义下

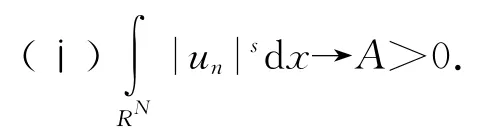
（ⅱ）存在｛yn｝⊂ℕN，使得⇀u≠0于H2（RN）且

引理1．6的证明 （ⅰ）由引理1．2（ⅱ），‖un‖H2有界．

由（f1），（f2），对于∀ε＞0，∃Cε＞0使得，故

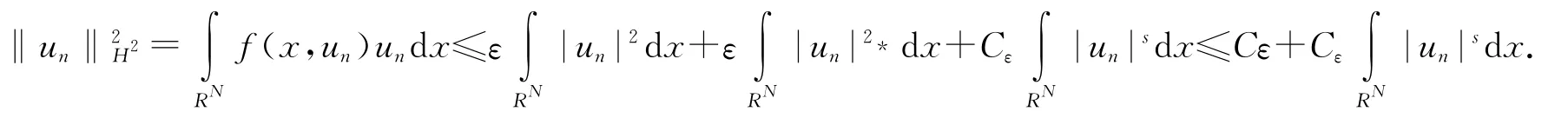
（ⅱ）由引理1．2（ⅲ），存在｛yn｝⊂ℕN，使得）．我们对运用集中紧原理（见参考文献［7］），存在｛xn｝⊂RN，α∈（0，1］使得对于∀ε＞0，∃R＞0对于一切r′≥r＞0，有

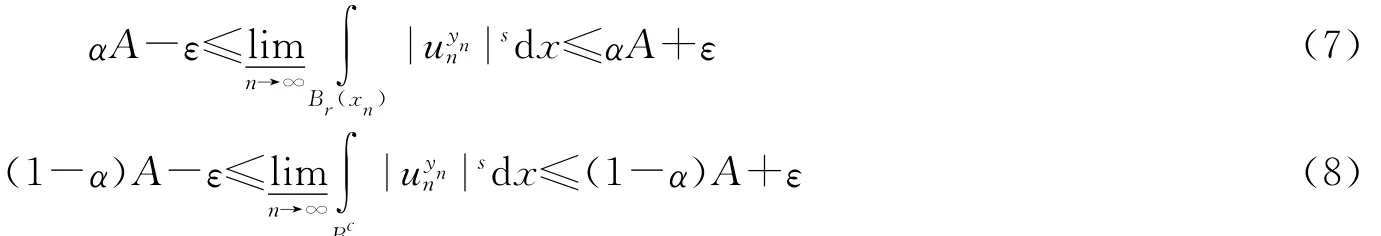
其中

下面证明α＝1，假设α∈（0，1），选取εn→0，rn→∞且r′n＝4rn，令0≤ξ≤1是一个光滑截断函数，当t≤1或t≥4时，ξ（t）＝0，当2≤t≤3时，ξ（t）＝1，且｜ξ′（t）｜，｜ξ″（t）｜≤C．定义．由（7）～（8）式可知，再结合（f1），（f2）可知

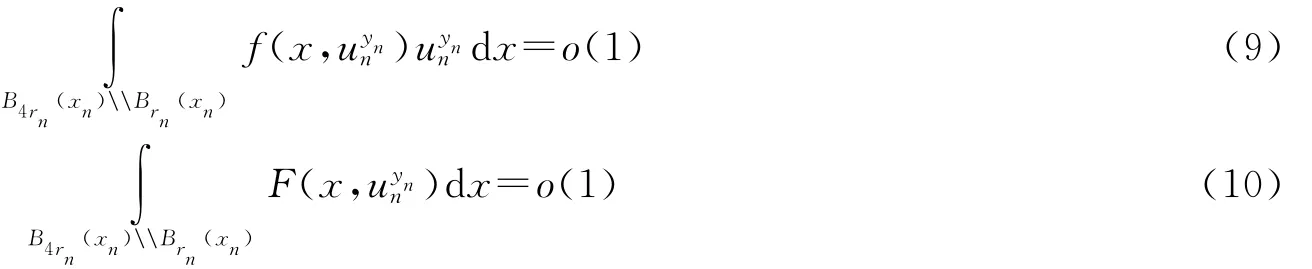
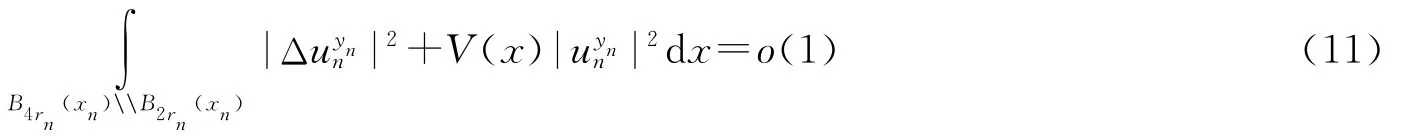
由（9）式，结合方程可以得到

令0≤η≤1是另一个光滑截断函数，当t≥3时，η（t）＝0，当t≤2时，η（t）＝0，且｜η′（t）｜，｜η″（t）｜≤C，记wn＝，由（9）式，（11）式可知

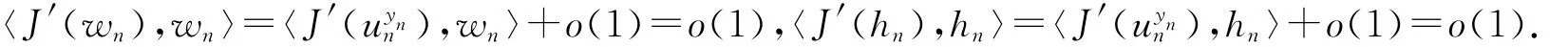
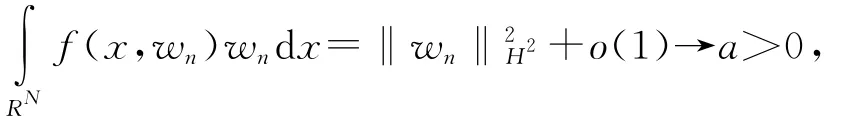
下面说明｛xn｝⊂RN有界，否则对任意固定的r＞0，如果n足够大，有Br（xn）⊂（0），则当r够大时，结合（8）式，ε，再令r→∞，这意味着u＝0，矛盾，故｛xn｝⊂RN必须有界．故可以选取有界集K使得对于任意固定的r都有Br（xn）⊂K，再结合（7）式可知，

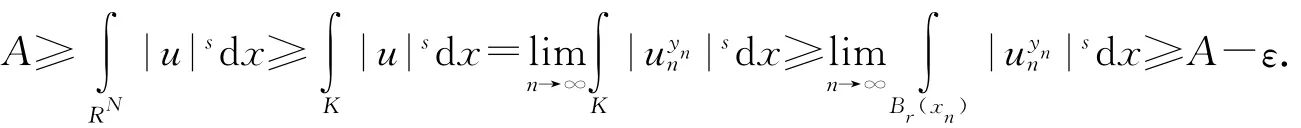
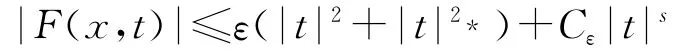
利用Fatou引理可知，（ⅱ）成立．

最后类似于引理1．5最后一段的证明，我们可以得到方程（1）的基态解的存在性，从而完成了定理的证明．

［1］Ambrosetti A，Rabinowitz P H．Dual variational methods in critical point theory and applications［J］．J Funct Anal，1973，14：349－381．

［2］Liu Z，Wang Z Q．On the Ambrosetti－Rabinowitz superlinear condition［J］．Adv Nonlinear Stud，2004（4）：561－572．

［3］Li Y Q，Wang Z Q，Zeng J．Ground states of nonlinear Schrodinger equations with potentials［J］．Ann Inst H Poincare Anal Non Lineaire，2006，23：829－837．

［4］Willem M．Minimax theorems［M］．Boston：Birkhauser，1997：73．

［5］Lions P L．The concentration－compactness principle in the calculus of variations：the locally compact case：part 2［J］．Ann Inst H Poincare Anal Non Lineaire，1984（2）：223－283．

［6］Rabinowitz P H．On a class of nonlinear Schrodinger equations［J］．Z Angew Math Phys，1992，43：270－291．

［7］Lions P L．The concentration－compactness principle in the calculus of variations：the locally compact case：part 1［J］．Ann Inst H Poincare Anal Non Lineaire，1984（2）：109－145．