干扰对消系统的非零带宽性能与延时匹配
2014-10-27蒋云昊陈炜峰钟水明贾红云曹永娟毛鹏
蒋云昊,陈炜峰,钟水明,贾红云,曹永娟,毛鹏
(1. 南京信息工程大学 信息与控制学院,江苏 南京 210044;2. 南京信息工程大学 计算机与软件学院,江苏 南京 210044)
1 引言
共平台通信系统天线密集,而空间有限。当多台发射机和接收机同时工作时,发射机会对接收机产生严重的干扰,影响接收机对有用信号的接收,甚至阻塞接收机,使接收机不能正常工作。传统的解决办法是使发射机和接收机分时分频工作,这将大大降低通信系统的效能。自适应干扰对消技术是解决该问题新的有效途径,由于军事用途,可见的报道较少。
自适应干扰对消技术的理论基础源于 Widrow B等早先对自适应噪声对消理论的研究和LMS算法[1]。Glover J研究了自适应噪声对消系统的数字频域特性,给出了系统的数字频域近似模型[2]。LMS算法简单,易于实现,得到了广泛应用。但也存在收敛慢,失调大等问题,在对 LMS算法进行深入研究后,人们又提出改进算法,以提高和改善算法的性能[3~10]。杜武林等跟踪研究了自适应干扰对消技术,指出了该技术的基本原理、关键技术以及在军事通信应用中的重要意义[11]。郑伟强等讨论了开环前馈和闭环反馈的干扰对消,并指出解决大功率强耦合干扰(如舰载、机载通信系统的干扰)的干扰对消系统采用 LMS算法的模拟实现较为合适,文中还提出一种适合大功率应用的步进衰减器,以解决由PIN二极管构成的电调衰减器存在大功率下的非线性失真问题[12]。马义广等对自适应干扰对消系统在单频干扰信号下的性能进行了分析,并给出了系统的设计思路[13]。German.F等人研究了共平台干扰的自动测量预测分析技术[14]。文献[15]研究了实际系统中正交功分器非正交对系统暂态和稳态性能的影响。文献[16]讨论了零漂抑制方法对干扰对消系统带来的影响。由于实际干扰信号有一定的带宽,而且宽带通信日益发展,因此有必要研究模拟实现的自适应干扰对消系统对具有一定带宽干扰信号的对消性能和提高对消带宽的方法。
本文对干扰信号为一般形式下,自适应干扰对消系统的性能进行了分析,给出了系统的频域模型,并从时域角度研究了系统的收敛特性和稳态特性,最后给出提高对消带宽的方法。
2 系统模型
自适应干扰对消系统组成如图1所示,相关器由乘法器和积分器构成。相应的自适应干扰对消系统原理框如图2所示。
XI(t)为接收天线接收到的干扰信号,Xε(t)为对消剩余信号,Xs1(t)和Xs2(t)为耦合器I提取的信号经过功分器后的两路参考信号,W1(t)和W2(t)为权值,Y1(t)和Y2(t)为加权输出信号,Y(t)为合成信号,k为权值控制支路增益,积分器表示为1/τ1s,τ1为时间常数。

图1 自适应干扰对消系统组成
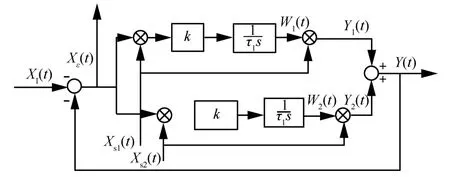
图2 对消系统原理
假设参考信号的一般形式为
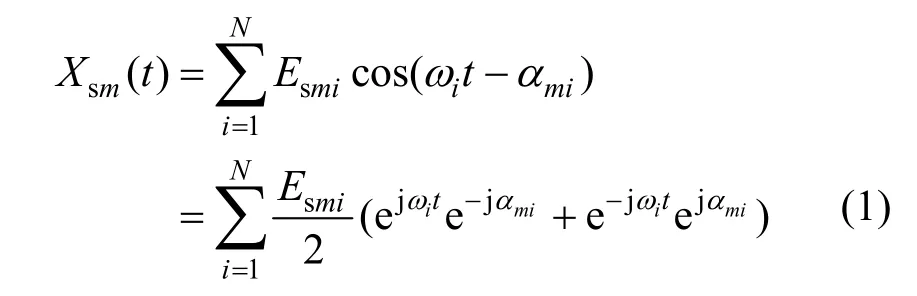
其中,Esmi是m(m=1,2)路参考信号第i个频率分量的幅值(单位 V);ωi为角频率(单位 rad/s);αmi是初相位(单位rad);N为参考信号所含频率分量个数。
干扰信号为
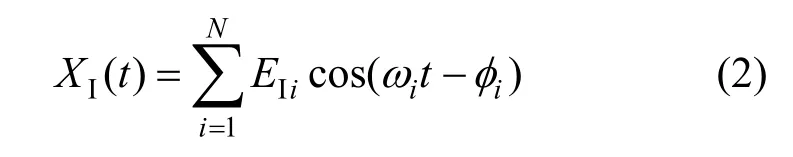
其中,EIi是干扰信号第 i个频率分量的幅值(单位V);ωi为干扰信号角频率(单位rad/s);φi是干扰信号初相位(单位rad)。
由图2可知,对消剩余干扰信号可表示为

3 频域分析
为从频域角度分析系统特性,以下根据文献[15]对单频干扰信号的干扰对消系统频域建模方法,推导非零带宽干扰信号自适应干扰对消系统的频域模型。由图2、式(1)和式(3)可得剩余干扰信号和参考信号乘积为

用 E(s)表示 Xε(t)的 Laplace变换,并利用Laplace位移性质可得
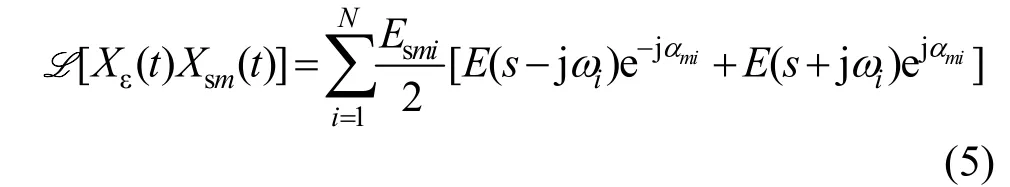
由图2可得,权值为
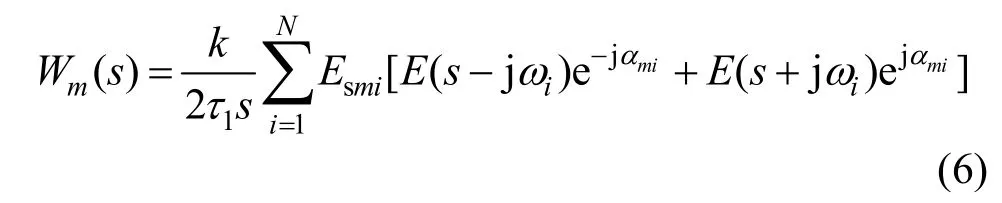
权值和参考信号乘积的Laplace变换为
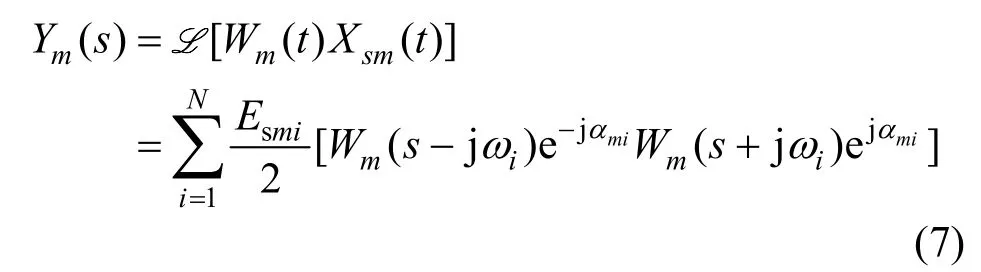
将式(6)代入式(7)可得

由式(8)及图2可得,合成信号Y(s)为
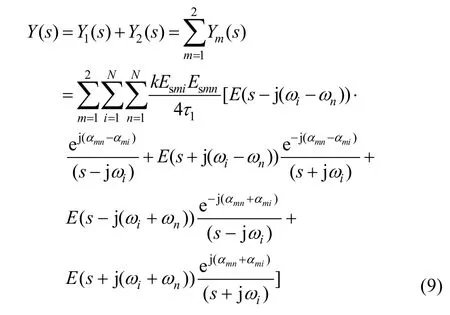
如图1所示,由于参考信号Xs1(t)和Xs2(t)是正交功分器的输出信号,所以两者等幅正交,因此有

由于两参考信号幅值相等,统一定义为Esi。由式(10)可得 α1n−α1i=α2n−α2i,并统一定义为αn−αi。
将式(12)代入式(9),合成信号Y(s)的频域表示可简化为
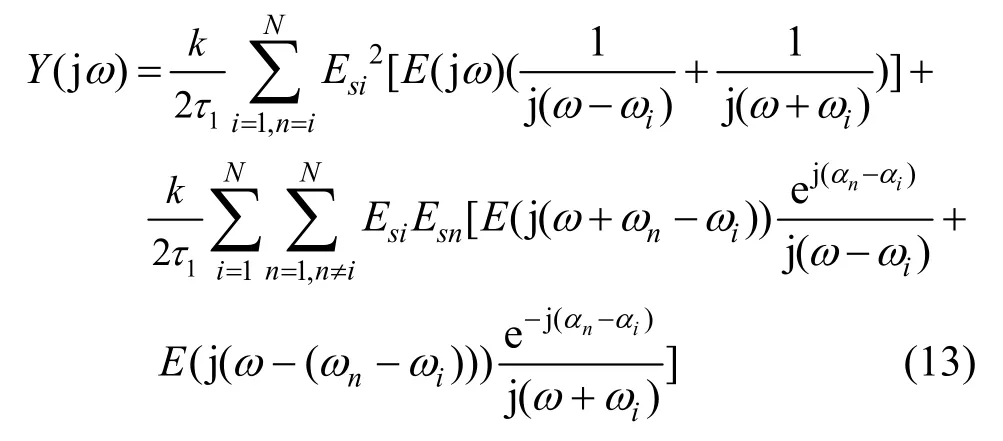
由于式(13)中E(j(ω+ωn−ωi))和 E(j(ω−(ωn−ωi))为频移项,系统本质上是时变的,难以写出Y(jω)/E(jω)的闭合表达式。若干扰信号为窄带信号,即
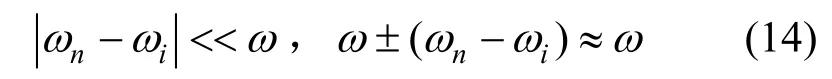
则式(13)可近似为
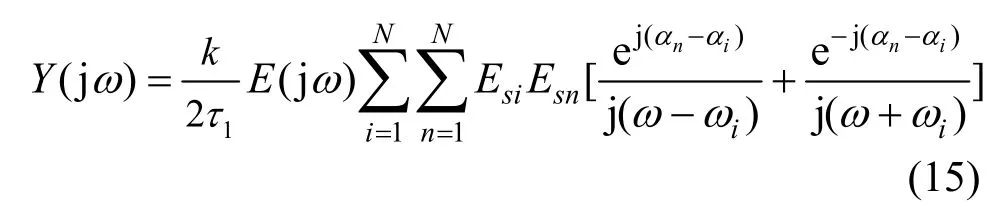
可得合成信号Y(s)至剩余干扰信号E(s)的传函为
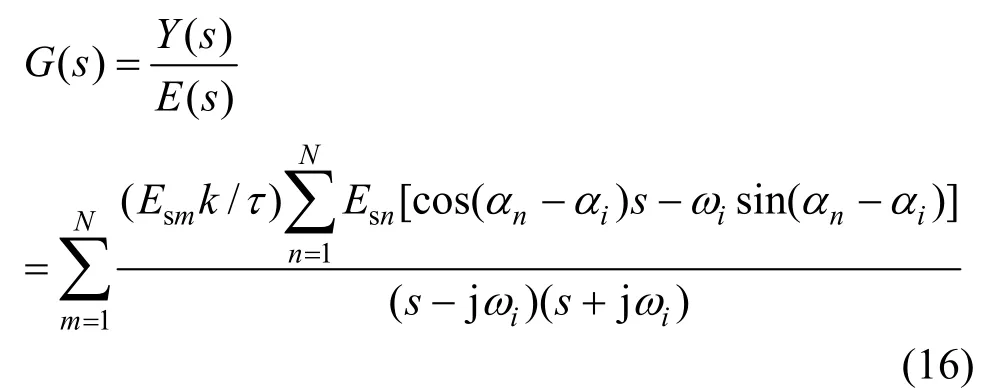
式(16)展开求和可得
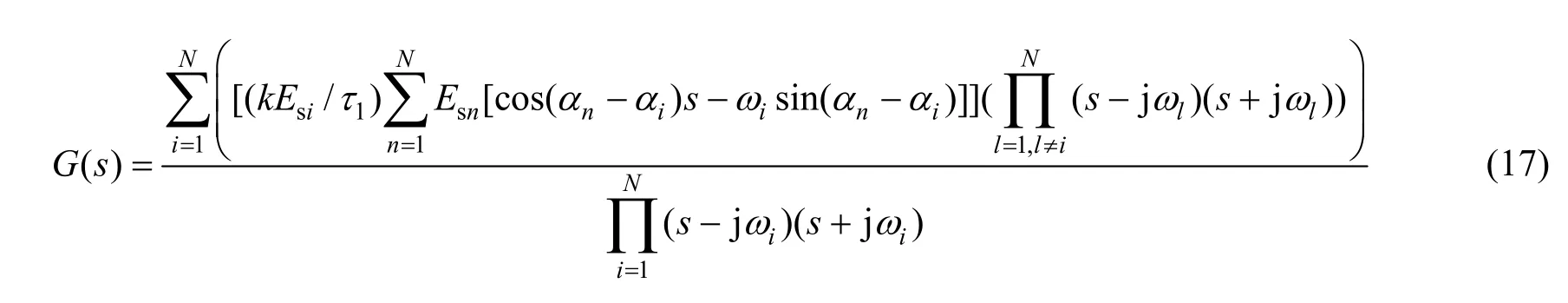
由图2和式(17)可知,剩余干扰信号E(s)至输入XI(s)的闭环传函为
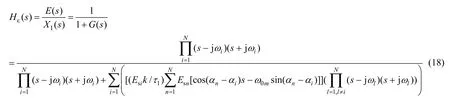
由式(18)可见,若干扰信号为窄带信号,满足式(14),则系统可近似为在每个干扰信号频率点ωi都有零点的梳状滤波器。如果干扰信号频率发生变化,滤波器的陷波频率也自适应变化,能够实现对干扰信号的自适应对消。若干扰信号带宽较宽,不满足式(14),则由于系统时变,将得不出式(18)的闭环传函形式。为了进一步研究干扰信号为一般形式时系统的对消特性,以下将从时域进行分析。
4 时域分析
由图2和式(1)可得,2个正交参考信号可表示为

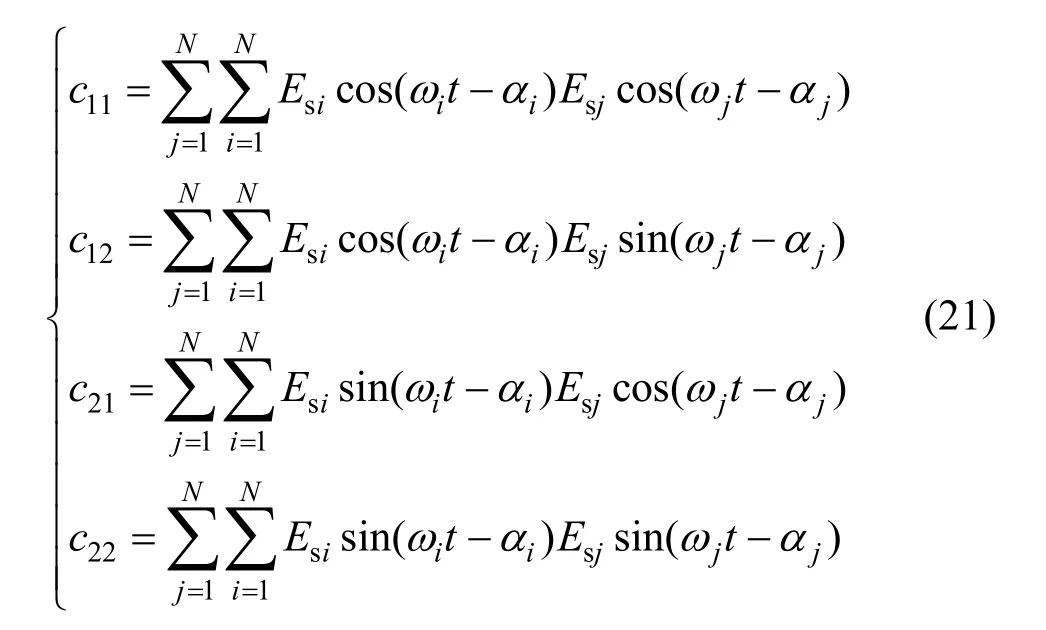
对式(20)取平均可得相关性为
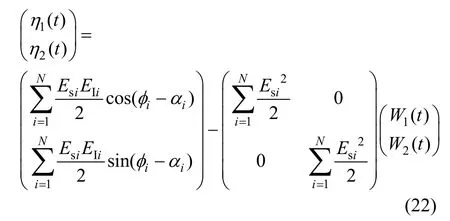
当相关性为零时,可得系统的最优权值为
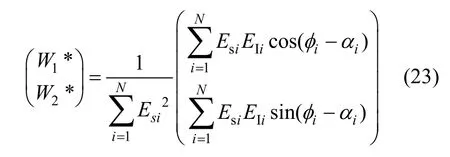
若系统能收敛至最优权值,则剩余干扰信号为


当N=1,即干扰信号为单频时,可得最优权值为
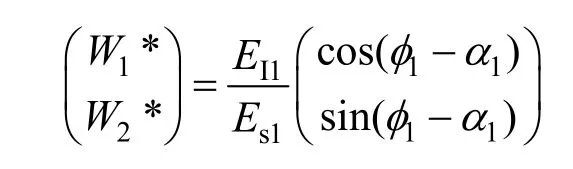
此时,剩余干扰信号为
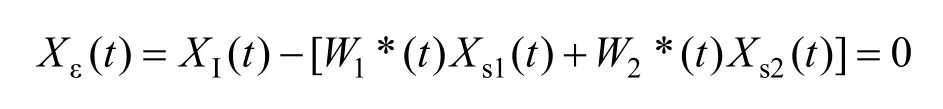
即在单频信号下,权值收敛到最优权值可使剩余干扰信号为零,这就是单频干扰信号下两权值自适应干扰对消系统的结论[14]。若N≠1,即干扰为非零带宽信号,由式(24)可知,即使在最优权值下,两权值自适应干扰对消系统的剩余干扰信号不为零,一般仍然含有N个频率的干扰信号。所以,当干扰信号不是单频信号时,利用两权值对消系统,理论上一般不可能将干扰对消至零。
以上未考虑实际系统的收敛过程,而直接根据最优权值进行分析。由于实际系统中的积分器具有低通特性,这里用低通代替积分进行分析。低通可表示为k1/(τ2s+1),k1=τ2/τ1为低通的增益,τ1、τ2为低通的2个时间常数。
如图 2 所示(用 k1/(τ2s+1)代替 1/τs),并考虑低通的输入输出关系,可得权值微分方程组为
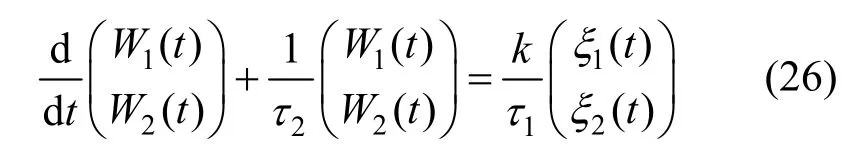
其中,ξ1(t)、ξ2(t)的表达式如式(20),为参考信号和剩余干扰信号的乘积。
将式(20)代入式(26)可得

根据式(21),将其展开可得

由式(28)可知,式(26)是一组时变微分方程组,直接求解困难,以下从平均模型进行分析。
对式(26)取平均,即忽略交流量,可得
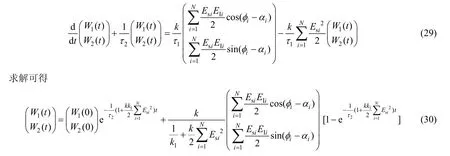
由式(30)可见,权值的收敛速度由指数项决定。提高系统增益k、低通增益k1和参考信号幅值可提高系统的收敛速度。
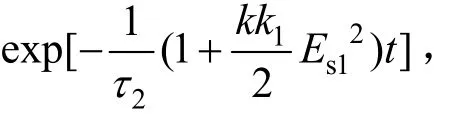
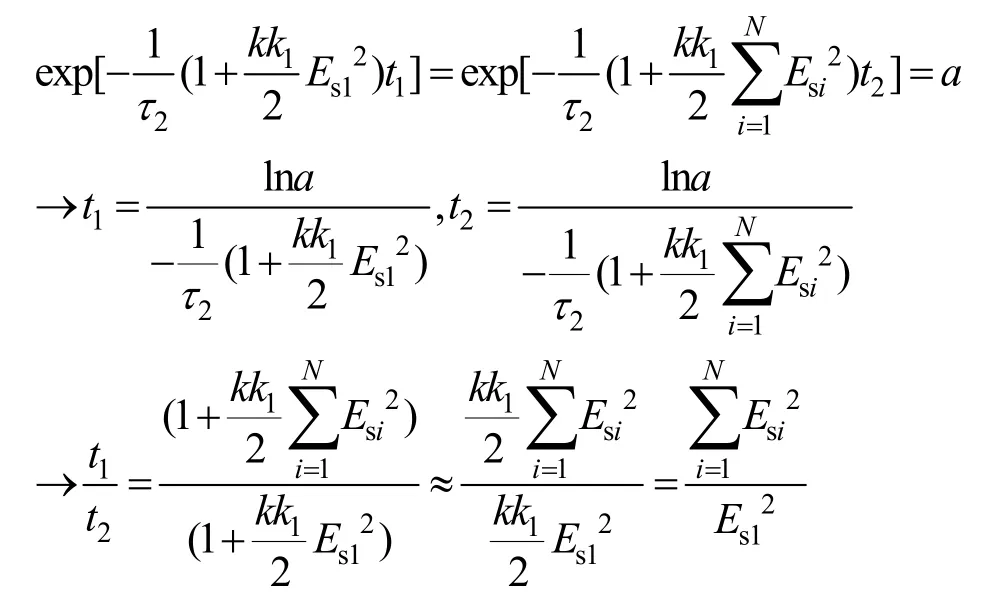
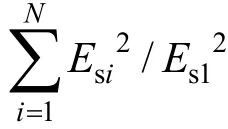
由式(30),当t→∞,可得稳态权值为
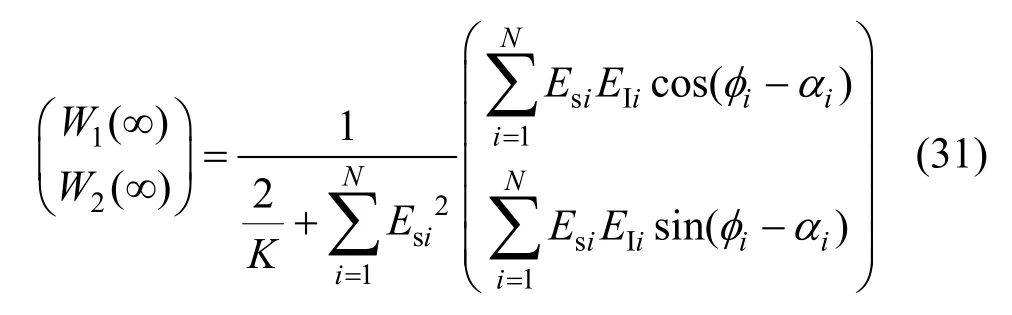
其中,K=k(τ2/τ1)=kk1。若 τ2→∞,则 K→∞,实际积分器变为理想积分器,式(31)与式(23)完全一致。
利用式(2)、式(3)、式(19)和式(31),可得稳态下,剩余干扰信号为

由式(32)、式(33)可见,此时剩余干扰信号仍然含有N个频率的信号,各频率分量的干扰对消比为

若K→∞,即积分器为理想积分器,式(33)与式(25)完全一致。此时剩余干扰信号仍然含有N个频率的信号。
5 延时匹配与宽带对消
如图1所示,两权值大功率强耦合干扰对消系统需要2个大功率电调衰减器和相应的干扰信号提取、权值控制和合成信号注入系统。从算法的角度,若要提高多频干扰信号(特别是宽带干扰信号)的对消性能,需要成倍增加权值,这将大大增加系统硬件实现的复杂性和成本。为提高干扰对消比和对消带宽,并能简化系统的实现,就需要研究其他解决方法。
由于 EIi=Esi/β[13](β为干扰信号空间耦合衰减系数,如图 1所示),根据式(2)、式(19),如果Φi-αi=0,即参考信号与接收干扰信号同相,则由式(33)可知
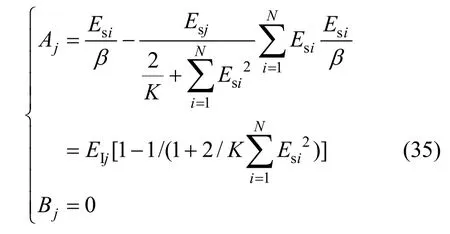
将式(35)代入式(32)可得此时剩余干扰信号为
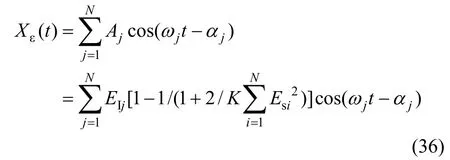
各频率干扰信号的干扰对消比为

由式(37)可知,延时匹配下,各干扰信号频率分量有近似相同的干扰对消比。若K→∞(相当于采用理想积分器),系统的剩余干扰信号为零,理论上干扰信号可被完全对消。只要匹配好干扰信号至耦合器II和参考信号至耦合器II的时延,就可以提高宽带信号的干扰对消比,且延时匹配越精确,对消效果越好,第6节将通过实例加以具体分析。因此,可以简便地在耦合器I至正交功分器间的信号提取支路上增加延时器来提高宽带干扰信号的对消效果。
6 仿真实例分析
以单频率调制信号为例,仿真参数如下。
参考信号
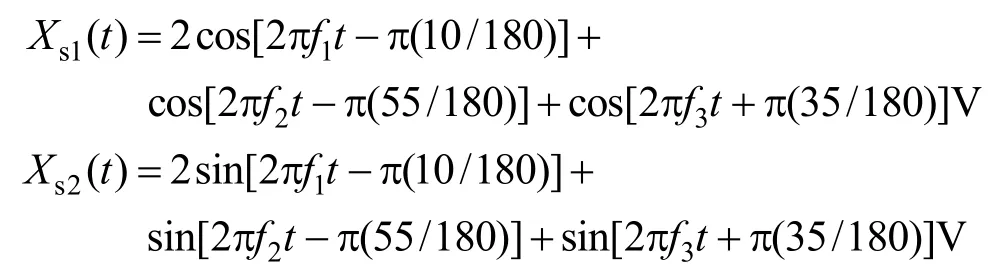
干扰信号
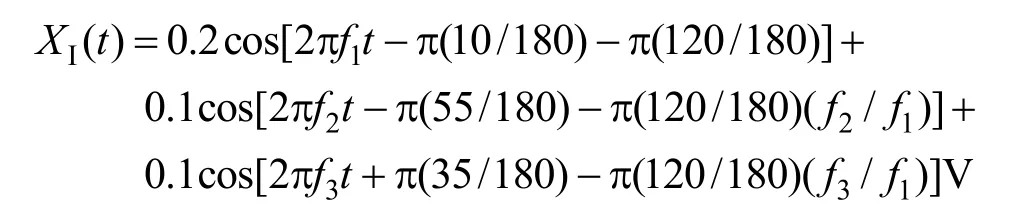
低通的2个时间常数分别取τ1=0.1 s,τ2=1 s,低通增益为k1=τ2/τ1=10,系统增益为k=100,f1=4 MHz。f2、f3为边带信号频率,取值如表1所示。表1中,2BW表示信号带宽,BW表示半信号带宽。为简化分析,仿真选择3个带宽值,即2BW分别为200 Hz、20 kHz和2 MHz,则对应的BW分别为100 Hz、10 kHz和1 MHz。

表1 信号带宽与对应频率
1)未延时匹配
干扰对消比随BW变化的计算和仿真结果如图3所示,其中横坐标取对数坐标。图中ICRcf1、ICRcf2、ICRcf3分别为理论计算(根据仿真参数,由式(33)、式(34)计算)得到f1、f2、f3频率分量干扰信号的干扰对消比随BW变化的曲线,其中BW取值范围为10 Hz~1 MHz。ICRsf1、ICRsf2、ICRsf3分别为仿真得到的f1、f2、f3频率分量干扰信号干扰对消比在BW分别为100 Hz、10 kHz和1 MHz时的结果。
由图 3可知,两边带干扰信号的干扰对消比随BW的变化规律基本一致。随着干扰信号带宽的增加,干扰对消比呈下降趋势,且带宽越大,下降越快。特别是随着干扰信号带宽的增加,边带信号的对消效果下降显著。图中的仿真结果和计算结果吻合较好。
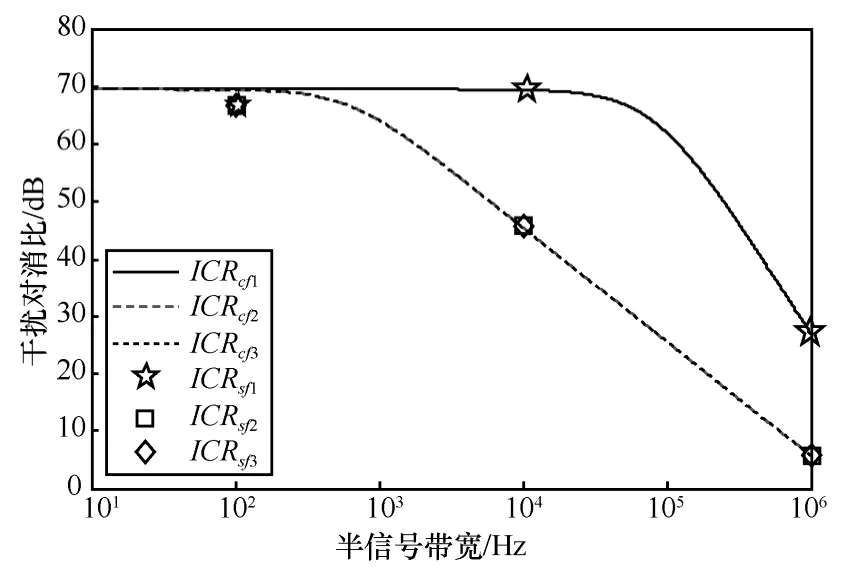
图3 干扰对消比随BW变化的计算和仿真结果(未延时匹配)
2)延时匹配
设延时匹配相位为γ,为便于分析,对γ取4组数据进行理论计算和仿真分析。根据仿真参数中参考信号和干扰信号的相位,当γ取0°时为未采用延时匹配;当γ取100°和115°时为未完全匹配;当γ取120°时为完全匹配。仿真和利用式(33)、式(34)计算得到的干扰对消比与BW和延时匹配程度间的关系如图4所示。简便起见,选取表1中最大的带宽(BW=1 MHz)进行仿真。
图4中分别表示3个频率分量的干扰对消比计算和仿真结果。当γ取0°时,未采用延时匹配,相应的计算和仿真结果与图3一致。当γ取100°和115°时,采取了一定的延时匹配,由图4可见,3个频率分量干扰对消比都有所提高。当γ取120°时,延时完全匹配,此时3个频率分量的干扰对消比相同,达到系统参数下干扰对消比的最大值。图中仿真结果与计算结果一致。
以BW=10 kHz、延时匹配γ=100°为例,边带干扰信号的干扰对消比提高了ΔICR≈15 dB。如果要求对消系统的边带干扰对消比不低于 60 dB,采用γ=100°的延时匹配后,对消带宽(BW)由原来的约2 kHz提高至约10 kHz,提高了5倍,ΔBW≈8 kHz。因此,采用简便的延时匹配方法可以显著提高系统的宽带干扰对消比和干扰对消带宽。
7 结束语
本文就干扰信号为非零带宽的一般信号下,自适应干扰对消系统的对消性能进行了理论分析,给出了系统的近似频域表达式和成立条件。从时域角度,推导出系统平均模型下的最优权值、稳态权值和各频率信号干扰对消比计算式。并给出通过延时匹配提高宽带对消比的方法。仿真分析证实了理论分析的正确性。文中分析的主要结论如下。
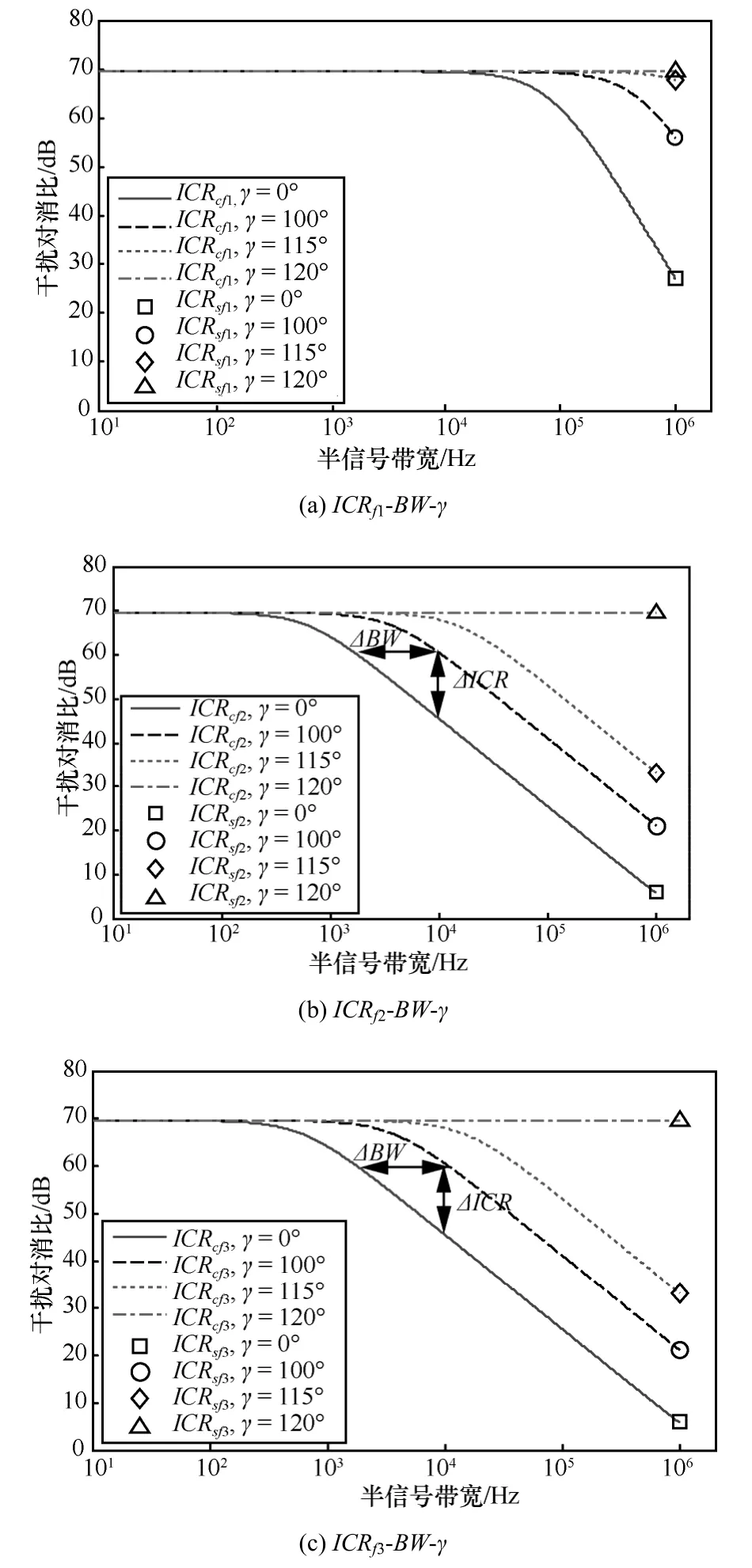
图4 干扰对消比与BW和延时匹配间关系的计算和仿真结果
1)对于非零带宽干扰信号,系统本质上是一时变系统,当带宽远小于中心频率,系统在理想积分方式下可近似为干扰信号各频率点具有陷波的自适应梳状滤波器,且带宽越窄,近似越准确。
2)系统的平均收敛速度除与权值控制支路增益、低通增益有关外,还与总参考信号幅值(各频率分量幅值平方和)有关,总参考信号幅值越大,系统的平均收敛速度越快。
对于非零带宽干扰信号,两权值系统在理论上一般不可能将干扰对消至零,并且干扰对消比随着干扰信号带宽的增大而减小,其中边带干扰对消性能的下降尤为明显。采用延时匹配的方法,可以显著提高系统的干扰对消带宽和宽带对消比,系统实现也相对简单。
[1]WIDROW B,GLOVER J R,MCCOOL J M. Adaptive noise cancelling: Principles and applications[J]. Proceedings of the IEEE,1975,63(12):1692-1716.
[2]GLOVER J R. Adaptive noise canceling applied to sinusoidal interferences[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing,1977,25(6):484-491.
[3]TOBIAS O J,SEARA R. On the LMS algorithm with constant and variable leakage factor in a nonlinear environment[J]. IEEE Transactions on Signal Processing,2006,54(9):3448-3458.
[4]AKHTAR M T,ABE M,KAWAMATA M. A new variable step size LMS algorithm-based method for improved online secondary path modeling in active noise control systems[J]. IEEE Transactions on Audio,Speech and Language Processing,2006,14(2):720-726.
[5]ZHANG Y,CHAMBERST J A,WANG W,et al. A new variable step-size LMS algorithm with robustness to nonstationary noise[A].IEEE International Conference on Acoustics,Speech and Signal Processing[C]. Piscataway,USA: IEEE Signal Processing Society,2007.1349-1352.
[6]DAS D P,PANDA G,KUO S M. New block filtered-X LMS algorithms for active noise control systems[J]. IET Signal Processing,2007,1(2):73-81.
[7]MUHAMMAD T A,MASAHIDE A,MASAYUKI K. A new variable step size LMS algorithm-based method for improved online secondary path modeling in active noise control systems[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing,2007,14(2):720-726.
[8]PASCHEDAG J,LOHMANN B. Error convergence of the filtered-X LMS algorithm for multiple harmonic excitation[J]. IEEE Transactions on Audio,Speech,and Language Processing,2008,16(5):989-999.
[9]DAS D P,PANDA G,KUO S M. New block filtered-X LMS algorithms for active noise control systems[J]. IET Signal Processing,2007,1(2):73-81.
[10]PASCHEDAG J,LOHMANN B. Error convergence of the filtered-X LMS algorithm for multiple harmonic excitation[J]. IEEE Transactions on Audio,Speech,and Language Processing,2008,16(5):989-999.
[11]杜武林. 干扰抵消技术的原理和应用[J]. 电信科学,1988,(5):51-55.DU W L. Principle and application of interference cancellation technology[J]. Telecom Science,1988,(5):51-55.
[12]郑伟强,杜武林. 自适应干扰抵消研究[J]. 电讯技术,1991,31(6):20-27.ZHENG W Q,DU W L. Study of adaptive interference canceling[J].Telecommunication Engineeting,1991,31(6):20-27.
[13]马义广,杜武林. 自适应干扰抵消系统的性能分析与设计[J]. 西安电子科技大学学报,1992,19(1): 84-92.MA Y G,DU W L. Performance analysis and design of adaptive interference canceling system[J]. Journal of Xi’dian University,1992,19(1):84-92.
[14]GERMAN F,ANNAMALAI K,YOUNG M,et al. Simulation and data management for cosite interference prediction[A]. IEEE International Symposium on Proc 2010 Electromagnetic Compatibility(EMC)[C]. 2010.869-874.
[15]JIANG Y H,MA W M,ZHAO Z H. Influence of non quadrature of phase shifter to adaptive interference cancellation system[A]. Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics[C]. Piscataway,USA: IEEE Computer Society,2009.359-363.
[16]蒋云昊,马伟明,赵治华. 斩波稳零下自适应干扰对消系统的性能分析[J]. 通信学报,2010,31(3):65-74.JIANG Y H,MA W M,ZHAO Z H. Analysis of chopping stabilizing zero for adaptive interference cancellation system[J]. Journal on Communications,2010,31(3): 65-74.
