浅谈确定防洪堤冲刷深度的几点体会

张 永

（新疆兵团勘测设计院（集团）有限责任公司 新疆 乌鲁木齐 830002）

1 工程概况

本次冲刷深度的讨论结合本人设计的云南省南汀河云县幸福段防洪工程来展开。南汀河流域位于云南省西南部，流域地处云贵高原西部的边缘，横断山脉南延段，整个流域地势呈北东向西南方向倾斜。云县幸福镇属中切割中山宽谷区，为河流冲积侵蚀型河谷。堤基位于河漫滩，是粗砂层，表层细颗粒含量较高，堤基承载力较低。工程防洪标准为10年一遇，防洪堤的级别为5级。其断面结构为：堤顶宽度3.0 m，前后堤坡坡比均为1∶2；迎水坡2年一遇洪水位以下采用格宾石笼挡墙护脚，护脚格宾挡墙高2.0 m～5.0 m；临水侧护坡采用30cm雷诺垫层护坡，背水侧护坡采用植草护坡。

2 防洪堤冲刷深度计算

2.1 按《堤防工程设计规范》（GB50286-2013）推荐公式计算

规范推荐公式如下：

式中，hs——局部冲刷深度，m；

Ho——冲刷处的水深，m；

Ucp——近岸垂线平均流速，m/s；

n——与防护岸坡在平面上的形状有关，取n=1/4；

η——水流流速不均匀系数，根据水流流向与岸坡坡交角查规范表D.2.2采用；

U——行进流速，m/s；

d50——床沙的中值粒径，m，取0.024；

γs、γ—泥沙与水的容重，k N/m 3，分别取值为19、10。

计算结果见表1。

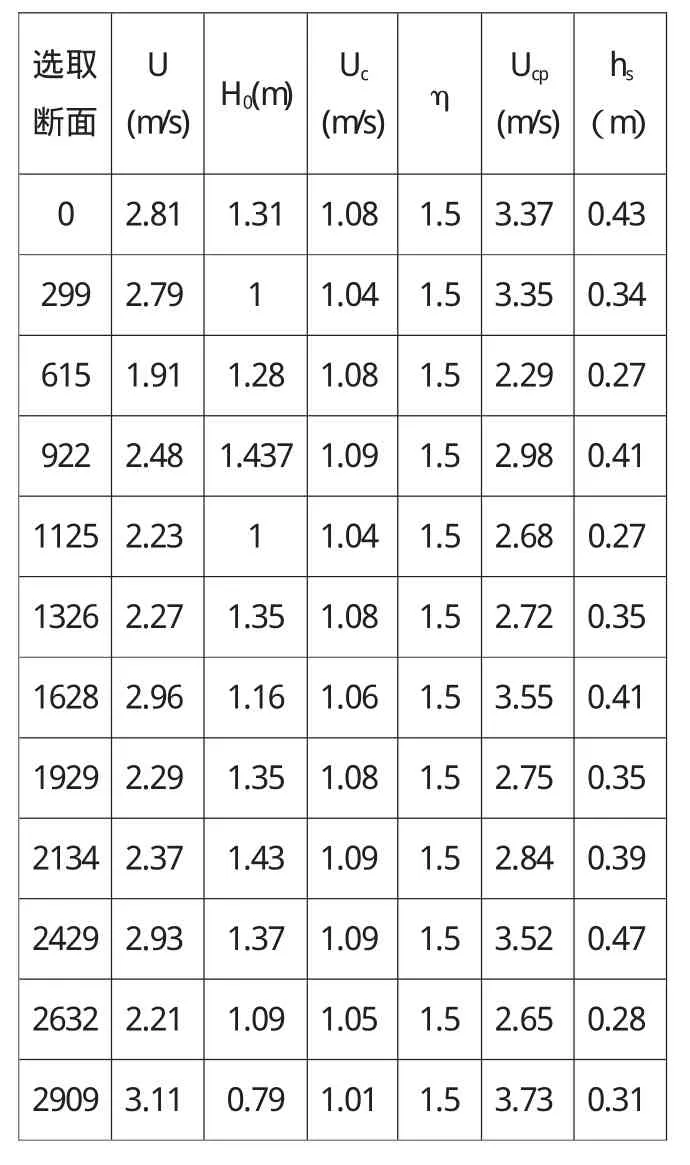
表1 《堤防工程设计规范》公式冲刷深度计算结果表

2.2 按《河道整治设计规范》（GB50707-2011）推荐公式计算

该公式对冲刷深度计算分水流平行于防护工程和水流斜冲防护工程两种情况分别计算。

2.2.1 水流平行于防护工程产生的冲刷深度计算

公式如下：

式中，△hB——局部冲刷深度，m；

hp——冲刷处冲刷前的水深，m；

Vcp——平均流速，m/s；

V允——河床面上允许不冲流速，m/s；

n——与防护岸坡在平面上的形状有关，取n=1/4。

计算结果见表2。

表2 《河道整治设计规范》公式平冲冲刷深度计算结果表

2.2.2 水流斜冲防护工程产生的冲刷深度计算公式如下：

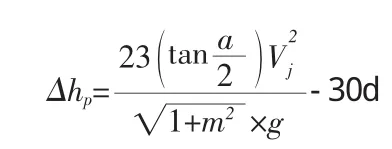
式中，△hp——从河底算起的局部冲刷深度，m；

α——水流流向与岸坡坡交角，30°；

m——防护建筑物迎水面边坡系数，2；

d15——坡脚处土壤计算粒径，m，0.05；

Vj—水流的局部冲刷流速，m/s，按有无滩地河床分别进行计算。

计算结果见表3。

表3 《河道整治设计规范》公式斜冲冲刷深度计算结果表

3 冲刷深度计算分析

（1）从公式形式来看，《河道整治设计规范》仍沿用旧版的《堤防工程设计规范》（GB50286-98），冲刷深度计算分水流平行于防护工程和水流斜冲防护工程两种情况进行计算。而新版的《堤防工程设计规范》（GB50286-2013）则采用一个公式来进行计算，但从其实际计算过程的取值来看，该公式实际上是将平冲和斜冲两种情况统一考虑，计算过程更为简单明了。

（2）从计算过程取值来看，部分取值实际操作较困难。

①《河道整治设计规范》中对水流的局部冲刷流速Vj的计算，该规范对Vj的计算分为有无滩地的两情况。对于滩地界限的划分本身就比较难确定，而对于很多游荡摇摆性的河流，滩地又可能会经常发生变化。而这些都将影响冲刷深度计算结果与实际是否相符。

②对于冲刷深度起算位置的确定，在《河道整治设计规范》中，当计算斜冲时，明确是从河底算起的局部冲刷深度；而当计算平冲时，则仅写为局部冲刷深度，从何处算起并没有说明。《堤防工程设计规范》也仅写为局部冲刷深度，没有明确。本人目前计算时均将其视为从河底算起的局部冲刷深度。

③规范上计算冲刷深度时采用现状河床面上堤脚处的泥沙粒径和允许不冲流速或起动流速，而实际操作中，大部分是将原堤脚开挖料再回填至堤脚，对于冲刷深度较大，堤脚基础下得较深，而河床地层岩性又存在分层的情况，则很可能导致河床面上的粒径、允许不冲流速和起动流速发生了较大变化，从而使原计算的冲刷深度与实际不符。是否需对新回填的堤脚土的冲刷深度重新计算，如果小于原设计的冲刷深度尚可，但若大于原设计的冲刷深度该如何处理。

（3）从计算结果来看，《河道整治设计规范》冲刷深度计算值要大于《堤防工程设计规范》。

①《河道整治设计规范》的水流平行于防护工程的冲刷深度计算结果比《堤防工程设计规范》的计算结果稍大。究其原因，《河道整治设计规范》采用的是平均流速与河床面上允许不冲流速的比值，《堤防工程设计规范》采用的是平均流速与泥沙起动流速的比值。允许不冲流速是指使河床泥沙不被水流冲刷破坏的最大断面平均流速，主要与河床泥沙和水流的含沙量有关。对清水水流可直接从第二版的《水力计算手册》上查询，对挟沙水流该手册上推荐了根据我国部分渠道实测资料总结出来的经验公式。泥沙起动流速是指静止于河床表面的泥沙颗粒，当水流强度逐渐增加大某一临界值时，泥沙颗粒就会开始运动，此时的水流强度即为泥沙起动流速。天然河流中泥沙颗粒的形状、大小不同，与其他颗粒的相对位置都是随机的，另外，在天然河流中，水流都具有脉动的性质，即作用在某一指定位置上颗粒的力也完全是随机的，因此床面上某一指定位置的泥沙颗粒的起动具有双重的随机性。起动流速公式其实质就是相对某一起动概率下的起动流速。对于两本规范分别采用河床面上允许不冲流速和泥沙起动流速来进行冲刷深度的计算到底哪一个更符合实际，由于本人水平有限，目前不敢轻易下结论，有待实践进一步验证。

②《河道整治设计规范》水流斜冲防护工程的冲刷深度计算结果则明显大于《堤防工程设计规范》计算结果。产生较大差异的原因，笔者认为，水流斜冲防护工程冲刷深度计算公式中，当河床坡脚处粒径较小时，斜冲冲刷深度计算结果几乎只与水流流向与岸坡的夹角和水流流速有关，而基本与河床地质情况无关，忽视了河床本身抵抗冲刷的能力，导致其计算结果明显大于《堤防工程设计规范》的计算结果。但从本工程附近已实施的防洪堤实际调查情况来看，《堤防工程设计规范》的计算结果更符合实际。

4 结语

冲刷深度计算是个比较复杂的过程，不能简单地套公式进行计算，要结合当地的实际情况，对已发生的冲刷水毁情况要进行调查，不能对整个工程冲刷深度的确定搞一刀切。就现行规范中某些参数的取值以及包括推荐的两种计算公式究竟取哪一种，目前也没有明确的说法，笔者认为，考虑现在气候异常，在用两种公式计算的基础上结合实际，在满足规范的前提下取大值以利安全。

［1］《河道整治设计规范》（GB 50707-2011）[S].

［2］《堤防工程设计规范》（GB 50286-2013）[S].

［3］王兴奎等，河流动力学[M]，北京：科学出版社，2004.

［4］李炜等，水力计算手册[M]，北京：中国水利水电出版社，2006.