Cl0，2k＋1的张量积分解式与矩阵表示

宋元凤，李武明

（1.吉林大学 数学学院，长春130012；2.通化师范学院 数学学院，吉林 通化134002）

Clifford代数在高维几何、理论物理、编码理论、机器人科学和地理科学等领域应用广泛［1－2］.设Clp，q为ℝp，q上的实 Clifford代数，Lee等［3－4］给出了实 Clifford代数Cl0，3的一种矩阵表示；曹文胜［5］给出了Cl0，3的另外两种矩阵表示，并探讨了其运算性质；文献［6］给出了实Clifford代数Clp，q的张量积表达式与矩阵表示，其中把实Clifford代数Clp，q的中心作为张量积分解式的一个因子.本文把文献［6］的结果进一步细化，给出了实Clifford代数Cl0，2k＋1的张量积分解式及矩阵表示.当Cl0，2k＋1的中心同构于ℂ时，得到了“Cl0，2k＋1同构于Cl1，1的k次张量幂和Cl0，1的张量积”的结论，并利用该结果得到Cl0，2k＋1的矩阵表示，由于此时Cl0，2k＋1为单代数［7］，所以在同构意义下Cl0，2k＋1的矩阵表示是唯一的.当Cl0，2k＋1的中心同构于ℝ与ℝ的直和时，得到了Cl0，2k＋1的张量积分解与矩阵表示，但此时矩阵表示不一定是唯一的.结合上述两种情况，得到了本文的主要结果：

其中：k为非负整数；2k＋1≡αmod 8；δ＝［1－｛α／3｝］.特别地，当2k＋1＝3时，可得一种与文献［3－5］形式不同的矩阵表示.

本文HH 表示四元数，⊗kCl1，1表示Cl1，1的k次张量幂，Cen（Clp，q）表示实 Clifford代数Clp，q的中心，e12…s为Cl0，2k＋1的s次单位向量，Mat（2，ℝ）表示2阶实矩阵代数，｛a｝表示实数a的小数部分，［a］表示实数a的整数部分，其他符号参见文献［8－9］.

1 Cl0，2k＋1的张量积分解

设｛e1，e2，…，ep＋q｝是ℝp，q的一组标准正交基，Clp，q上的Clifford乘积定义为

因此实 Clifford代数Clp，q是2p＋q维结合代数［8］.

本文从中心同构于ℂ和ℝ与ℝ直和两种情况探讨Cl0，2k＋1的张量积分解，首先给出中心同构于ℂ和ℝ与ℝ直和的充要条件.

引理1 设k是非负整数，则如下3个结论等价：

1）Cen（Cl0，2k＋1）同构于二维实代数ℂ；

证明：设e12…（2k＋1）为Cl0，2k＋1的2k＋1次单位向量，则

根据文献［6］经简单计算即可得结论.

引理2 设k是非负整数，则如下3个结论等价：

1）Cen（Cl0，2k＋1）同构于二维实代数ℝ⊕ℝ；

证明类似于引理1.

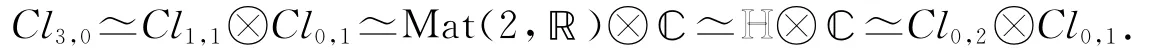
事实上，Cl3，0可视为由〈e1，e2〉和〈e123〉的乘积生成，而

经简单的张量积验证易知

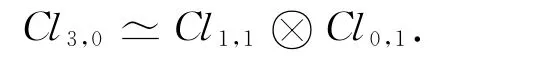
Cl3，0也可视为由〈e12，e13〉和〈e123〉的乘积生成，而

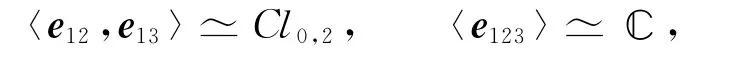
经简单的张量积验证易知

注1 引理3的内容可参见文献［8］中第四章与第十七章，为考察Cl3，0的结构本文给出了Cl3，0的另一种证明.

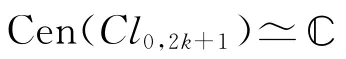
所以当2k＋1≡1mod 8时，式（3）成立.当2k＋1≡5mod 8时，由引理3有

由文献［6］经简单计算可得如下引理.

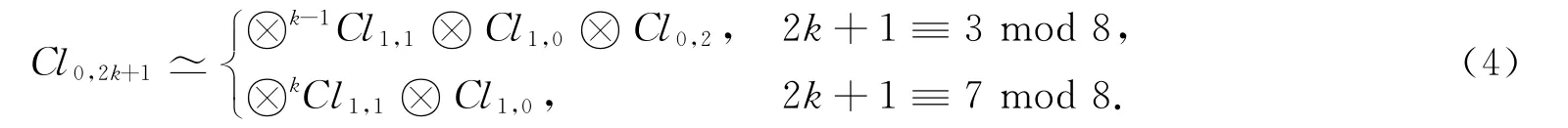
结合引理4和引理5可给出Cl0，2k＋1的张量积分解式：

定理1 设k是非负整数，则

其中：2k＋1≡αmod 8；δ＝［1－｛α／3｝］.

2 Cl0，2k＋1的矩阵表示

定义1［10］设A 是有限维F－代数，V 是有限维F－向量空间.如果存在 F－代数同态ρ：A→EndF（V），则称（V，ρ）是A的一个F－表示.

定义2［10］如果存在F－线性同构f：M→N，使得∀a∈A，fρ（a）＝η（a）f，则称A的两个F－表示（M，ρ）和（N，η）等价.

设Fm表示域F上的m 阶全矩阵代数.对于A＝（aij）∈Fm，B＝（bij）∈Fn，记

或

设

引理6 当 Cen（Cl0，2k＋1）≃ℂ时，

证明：因为

所以当 Cen（Cl0，2k＋1）≃ℂ时，

引理7 设 Cen（Cl0，2k＋1）≃ℝ⊕ℝ.

1）如果2k＋1≡7mod 8，则

2）如果2k＋1≡3mod 8，则

证明：1）如果2k＋1≡7mod 8，则有式（3）.因为

所以

2）如果2k＋1≡3mod 8，则

因为

所以

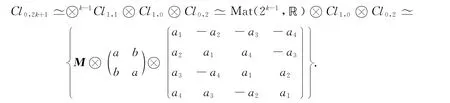
特别地，当2k＋1＝3时，

又

结合引理6和引理7可得：

定理2 设k是非负整数，

其中：2k＋1≡αmod 8；δ＝［1－｛α／3｝］.

［1］Baylis W E.Clifford（Geometric）Algebras with Applications to Physics，Mathematics and Engineering［M］.Boston：Birkhäuser，1996.

［2］Corrochano E B，Sobczyk G.Geometric Algebrawith Applications in Science and Engeneering［M］.Boston：Birkhäuser，2001.

［3］Lee D H，Song Y K.The Matrix Representation of Clifford Algebra［J］.J Chungcheong Math Soc，2010，23（2）：363－368.

［4］Lee D H，Song Y K.Applications of Matrix Algebrato Clifford Groups［J］.Adv Appl Clifford Algebra，2012，22（2）：391－398.

［5］CAO Wen－sheng.Similarity and Consimilarity of Elements in 4－Dimensional Clifford Algebra ［J］.Acta MathematicaScientia，2010，30A（2）：531－541.（曹文胜.四维 Clifford代数的相似与合相似 ［J］.数学物理学报，2010，30A（2）：531－541.）

［6］SONG Yuan－feng，DU Xian－kun，LI Wu－ming.Real Clifford Algebras as Tensor Products over Centers［J］.Adv Appl Clifford Algebra，2013，23（3）：607－613.

［7］刘绍学，郭晋云，朱彬，等.环与代数 ［M］.2版.北京：科学出版社，2009.

［8］Lounesto P.Clifford Algebras and Spinors［M］.2nd ed.Cambridge：Cambridge University Press，2001.

［9］Gallier J.Clifford Algebras，Clifford Groups and aGeneralization of the Quaternions：The Pin and Spin Groups［D／OL］.2013－11－12.http：／／arxiv.org／pdf／0805.311v2.pdf.

［10］冯克勤，章璞，李尚志，等.群与代数表示引论 ［M］.2版.合肥：中国科学技术大学出版社，2003.