基于MATLAB的光电转换分析

付敏 陈军峰 侯学华

【摘要】本文首先介绍了在能源危机的大背景下，太阳能光伏发电的重要性。主要分析了光伏电池的电路模型，推导出光伏电池的电流输出和功率输出，然后利用MATLAB绘出光伏电池的U-I、U-P特性曲线，以及在不同光照和温度下的输出特性，最后对光伏电池最大功率点跟踪算法进行了简单介绍。

【关键词】太阳能;光伏电池;输出特性;最大功率点

一、引言

太阳能是一种新兴的绿色能源，以可靠耐用、维护成本低、安全且无污染等优点。但在应用中仍存在以下缺点。

（1）光伏阵列发电效率低。

（2）系统成本高。

（3）环境因素影响较大等。

面对以下难题，各个国家都在积极展开如何提高光伏电池组件的能量转换效率的研究并提出解决办法。

1.改造光伏电池的制造工艺。

2.对太阳光角度进行跟踪。

3.设计MPPT控制器。

二、光伏电池的电路模型分析

硅太阳能电池是使用最普遍的一种利用半导体光伏效应将太阳能直接转化为电能的光伏电源。为实现太阳能光伏发电系统，就要对硅太阳能电池的数学模型进行分析处理，以便对光伏系统进行研究和设计。

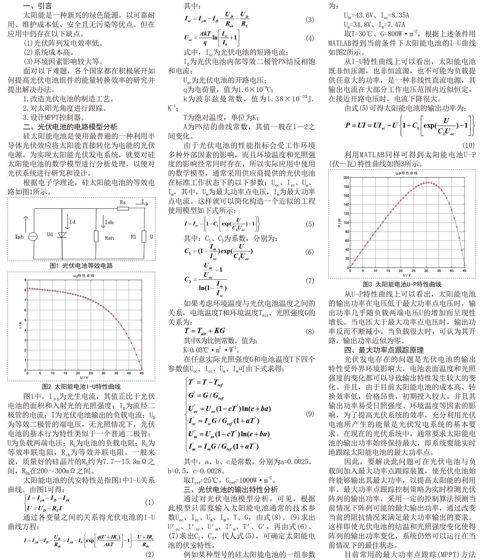
根据电子学理论，硅太阳能电池的等效电路如图1所示。

图1 光伏电池等效电路

图2 太阳能电池I-U特性曲线

图1中，Iρh为光生电流，其值正比于光伏电池的面积和入射光的光照强度;ID为流经二极管的电流;I为光伏电池输出的负载电流;UD为等效二极管的端电压，无光照情况下，光伏电池的基本行为特性类似于一个普通二极管;U为负载两端电压;RL为电池的负载电阻;RS为等效串联电阻，Rsh为等效并联电阻。一般来说，质量好的硅晶片的RS约为7.7～15.3mΩ之间，RSh在200～300mΩ之间。

太阳能电池的伏安特性是指图1中I-U关系曲线。由图1可得：

（1）

通过各变量之间的关系得光伏电池的I-U曲线方程：

（2）

其中：

（3）

（4）

式中，Isc为光伏电池的短路电流;

I0为光伏电池内部等效二极管PN结反相饱和电流;

Uoc为光伏电池的开路电压;

q为电荷量，值为1.6×10-9C;

k为波尔兹曼常数，值为1.38×10-23J.K-1;

T为绝对温度，单位为K;

A为PN结的曲线常数，其值一般在1—2之间变化。

由于光伏电池的性能指标会受工作环境多种外部因素的影响，而且环境温度和光照强度的影响经常同时存在，所以实际应用中使用的数学模型，通常采用供应商提供的光伏電池在标准工作状态下的以下参数：Uoc、Isc、Um、Im，其中，Um为最大功率点电压，Im为最大功率点电流。这样就可以简化构造一个近似的工程使用模型如下式所示：

（5）

其中：C1、C2为系数，分别为：

（6）

（7）

如果考虑环境温度与光伏电池温度之间的关系，电池温度T和环境温度Tair、光照强度G的关系为：

（8）

其中K为比例常数，值为：

K=0.03℃·m2 ·W-1。

在任意实际光照强度G和电池温度T下四个参数值Uoc、Isc、Um、Im可由下式求得：

（9）

其中，a、b、c是常数，分别为a=0.0025，b=0.5，c=0.0028。

取Tref=25℃，Gref=1000W·m-2。

三、光伏电池的输出特性分析

通过对光伏电池模型分析，可见，根据此模型只需要输入太阳能电池通常的技术参数Uoc、Isc、Um、Im、T、G，由式（8）、（9）求出U'oc、I'sc、U'm、I'm、T'、G'，再由式（6）、（7）求出C1、C2，代人式（5），可确定太阳能电池的伏安特性。

例如某种型号的硅太阳能电池的一组参数为：

Uoc=43.6V、Isc=8.35A

Um=34.8V、Im=7.47A

取T=30℃、G=800W·m-2，根据上述条件用MATLAB得到当前条件下太阳能电池的I-U曲线如图2所示。

从I-U特性曲线上可以看出，太阳能电池既非恒压源，也非恒流源，也不可能为负载提供任意大的功率，是一种非线性直流电源，其输出电流在大部分工作电压范围内近似恒定，在接近开路电压时，电流下降很大。

由式（5）可得太阳能电池的输出功率为：

（10）

利用MATLAB同样可得到太阳能电池U-P （伏—瓦）特性曲线如图3所示。

图3 太阳能电池U-P特性曲线

从U-P特性曲线上可以看出，太阳能电池的输出功率在电压低于最大功率点电压时，输出功率几乎随负载两端电压U的增加而呈现性增长。当电压大于最大功率点电压时，输出功率反而不断减小。当负载很大时，可认为其开路，输出功率近似为零。

四、最大功率点跟踪原理

光伏发电存在的问题是光伏电池的输出特性受外界环境影响大，电池表面温度和光照强度的变化都可以导致输出特性发生较大的变化。并且，由于目前太阳能电池的成本高、转换效率低，价格昂贵，初期投入较大。并且其输出功率易受日照强度、环境温度等因素的影响，为了提高光伏系统的效率，充分利用光伏电池所产生的能量是光伏发电系统的基本要求。在现在的光伏系统中，通常要求太阳能电池的输出功率始终保持最大，即系统要能实时地跟踪太阳能电池的最大功率点。

因此，要解决此问题可在光伏电池与负载间加入最大功率点跟踪装置，使光伏电池始终能够输出其最大功率，以提高太阳能的利用率。最大功率点跟踪控制策略为实时检测光伏阵列的输出功率，采用一定的控制算法预测当前情况下阵列可能的最大输出功率，通过改变当前的阻抗情况来满足最大功率输出的要求。这样即使光伏电池的结温和光照强度变化使得阵列的输出功率变化，系统仍然可以运行在当前情况下的最佳状态。

目前常用的最大功率点跟踪（MPPT）方法主要包括恒定电压法、扰动观察法、电导增量法、间歇扫描法、“上山法”等，主要通过测量电池的输出电压和输出电流。来判断输出功率的变化方向，从而调整电池工作状态向最大功率点位置移动。

传统的扰动观察法是通过不断的外加扰动电压来观察光伏电池的输出功率的变化，从而寻找最大功率点。参考图3通过改变光伏阵列的输出电压，观察其输出功率的变化，若扰动后的输出功率大于原输出功率，则表明此刻的扰动方向是正确的，应继续向该方向扰动;若扰动后的输出功率小于原输出功率，则表明当前扰动方向错误，应往反方向进行扰动。

參考文献

[1]赵乐.太阳能光伏发电系统能效控制研究[J].长安大学，2012，6.

[2]吴新江.基于Matlab/Simulink的聚光太阳能电池仿真[J].武汉理工大学，2012，4.

[3]任奇，李永晨，唐敏，夏东伟.单极式光伏并网发电系统的仿真与实验研究[J].电力电子技术，2008（42）.

[4]文韬，洪添胜，李震.太阳能硅光电池最大功率点跟踪算法的仿真及试验[J].农业工程学报，2012（28）.

[5]李明杨.独立光伏发电系统的控制策略及其应用研究[J].中南大学，2010，6.