基于多级CBF的长流识别

刘元珍

0 引言

高速网络因其速度快、数据量巨大而使得对网络流量的测量非常困难，在高速网络流量测量领域，采用各种算法针对不同应用的研究被广泛关注[1-4]。

在互联网中，由于少量的长流占据了网络流量的大部分，因此对长流的识别显得尤其重要，长流识别也成为研究热点。吴桦等[6]提出了基于双重Counter Bloom Filter的长流识别算法，使用两层Counter Bloom Filter结构将长流过滤和长流存在分开处理。YuZhang[5]提出Weighted Lossy Counting（WLC）方法，以常量时间（O(1)）识别出长流，并以大的存储空间获取高的精确率。

本文提出了基于多级 CBF的长流识别算法，首先对组成网络流的报文进行抽样，然后通过哈希映射查找被抽样的报文所属的流是否在长流信息表中，若存在则更新流信息表，若不存在则将抽样报文用多级CBF（Multistage Counting Bloom Filters，MSCBF）进行过滤，对各级CBF均达到阈值的抽样流，创建长流记录来维护该长流的信息，并将该流对应的各级CBF计数器减去阈值。多级CBF极大的降低了哈希冲突引起的误报率，而由于采用抽样和只对达到阈值的流进行长流信息维护，又有效的控制了资源损耗。第一节描述了长流及多级CBF，第二节描述了具体的长流识别算法，第三节对算法进行性能分析，第四节进行实验分析，最后一节总结全文。

1 长流及多级CBF

在网络中，流是指具有相同属性的报文的集合，属性一般采用源/宿IP地址、源/目的端口号、协议类型等。长流是指占据了大部分的网络通信量的流，但这部分流在数量上却相对较少。长流也可被定义为包含的报文数（字节数）超出了某个预先定义好的阈值的流。

Bloom Filter是一种哈希结构，支持集合元素查询，它的核心算法是一个V向量和一组哈希函数，使用长为m的位串V表达n个元素的集合 S= {s1,s2...sn}。使用k个哈希函数 hi，对于集合每个元素s，向量位串中对应于 h1( s) , h2(s ),...,hk(s )的位置被设置成1，否则为0。但在该向量位串中，存在某个位可能被多次置1，因此会导致某个元素不属于集合而被指称为属于集合，其概率误差称“p误报率”。经过一系列计算可得当 k=(m / n )ln2时，误报率err取得最小值 0.6185m/n。

标准Bloom Filter支持集合成员的插入和查询，但并不支持删除操(作)。计数型Bloom Filter即Counting Bloom Filter，以计数器 c i代替BF中的位，对于每个元素s，位串中对应的计数器值都增加1，删除该元素时则将对应的计数器值都减去1，从而在删除元素时不会修改其它元素的置位。

本文中的多级CBF（Multistage Counting Bloom Filters，MSCBF）使用并行的多级CBF，各级CBF采用相异的哈希函数组，虽然BF固有的误报率存在，但相异的哈希函数组在多级CBF匹配时可以极大减小误报率。

2 长流识别算法

长流识别首先在测量时间段内随机抽取 m个报文，然后通过多级CBF来识别报文数达到阈值的长流并使用长流信息表来维护这些长流的信息，多级CBF结构如图1所示：

图1 多级CBF结构

当一个报文被抽取时其所在的流也即被抽样，首先将抽取的报文通过经过一系列哈希映射得到哈希值作为地址指针，查找长流信息表中是否存在该流信息。若已存在，则更新该流信息。若不存在则将该报文通过多级CBF进行过滤，在每级CBF中，经过一系列哈希计算后，将对应的计数器加1。对各级CBF均达到阈值即 c( i)＞ =Tthd的抽样流，在流信息表中创建并维护该长流的信息，为了防止CBF溢出，创建了长流信息后，将该流对应的各级CBF计数器减去阈值。

算法的具体描述如下：

3 性能的分析

3.1 误报率及空间复杂度

通过一些具体数据对多级 CBF（MSCBF）的误报率及空间复杂度进行分析。

假设一个宽带为100MB/s的链路，有100000个活动的流，将阈值T定义为每秒流量大于链路传输容量的1%，即1MB。假设多级CBF中每级CBF有1000个计数器，那么一个不大于100KB的流通过MSCBF的可能性有多大呢？在一级CBF的情况下，这个流要通过，则其它的流必须要至少贡献 1M-100K=900KB（为了便于计算，按照1MB=1000KB计算）。在 1000个计数器中，最多有 99900/900=111个这样的计数器，因此，这个流能够通过一级CBF的概率为111/1000=11.1%。对于4级相互独立的CBF，一个不大于 100KB的流能够通过所有 4级 CBF的概率为(11.1%)4≈1.52×10-4。

因此，小于等于100KB的流能通过MSCBF被识别为长流的流数量大概为100000×(11.1%)4≈1.52×10-4＜16。 而在100KB/S链路情况下，大于100KB的流最多有999个，按照阈值T=1M的标准，这些流并不一定能够通过MSCBF。即使这些流全部通过，那么所有需要放入长流信息表的流的个数为：999+16=1015。所有通过MSCBF的流将被放入长流信息表中，根据以上分析，系统只需要为这些流分配1015个长流记录空间。

因此，为了处理100000个流，只需要4级CBF分配大约4000个计数器（每级1000个计数器）和大约1015个长流记录空间。

假设C为带宽，即整个测量时间段内的字节数；s为流的大小（单位Byte）；T为判断长流的阈值（单位Byte），b为一级CBF中的计数器个数，d为CBF的级数；n为当前活动流的个数。假设各级 CBF使用的哈希函数都是相异独立的，则一个大小s且s＜(T - C/ b)的流通过MSCBF的概率为ps，且有公式（1）：

若给定概率ps的要求，则可根据上式计算过 MSCBF级数d的大小。由于采用了多级CBF，成指数级得降低了单级CBF的误报率。

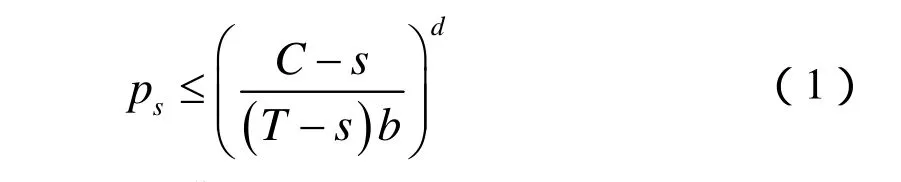
3.2 误差分析

基于多级CBF的算法主要误差来源自以下几个方面：抽样的误差、判断报文是否属于已知长流时哈希映射到长流信息表时产生的哈希冲突误差和多级CBF的误差。

抽样会带来不可避免的统计误差，根据抽样数据估计原始数据时，简单的可使用比例估计法，也可以使用复杂度高和更接近的 EM 算法，甚至在系统负载允许的情况下采用全流量测量，完全避免由抽样带来的误差。

判断报文是否属于已知长流时哈希映射到长流信息表时会产生哈希冲突而导致更新流信息的误差，但由于此时修改的流信息主要是报文数，对流信息的影响也主要是报文的数目即流长度，采用合理的哈希算法可以降低这一冲突。文献[5]中使用CBF称作Longflow_CBF来进行哈希运算，由于只需要进行查询操作，可使用标准BF，比CBF更节约空间，通过调整哈希函数和BF位串的长度来降低BF和CBF本身都固有的误报率，从而减小误差。

多级CBF结构的误差。对于属于某一长流的报文数目累计一定能达到阈值，因此也一定可以被识别，长流漏报率（false negative error）不存在，但存在误报率，即不是长流的流由于多级CBF的哈希累加可能被判定为长流。单级CBF的误报率与计数器的个数、不属于已知长流的报文集合数及哈希函数个数有关，但由于判断出某流是长流后，即将该流对应的计数器减去阈值，将流移到已知长流信息表，使集合样本减少，从而减小误报率。

4 实验分析

利用互联网公开提供的实际数据进行实验分析，其中，报文数超过1000的长流比例为0.17%。多级CBF的级数与其误报率最大值的关系如图2所示：

图2 多级CBF级数与误报率最大值关系

由于在子测量段结束时清空CBF及识别出长流后即将CBF计数器减去阈值，都会使多级CBF的实际误报率远小于误报率的最大值。当级数为1时，多级CBF退化成单级CBF。

5 总结

本文提出了一种基于多级CBF的长流识别算法，用多级 CBF结构来识别到达阈值的长流，可以有效的降低长流识别所需的存储空间，提高了长流识别的准确率，并可根据系统负载能力调整抽样率以满足更高的精度要求。

[1]周爱平,程光,郭晓军.高速网络流量测量方法[J].软件学报,2014.25(1):135-153.

[2]Sanjuàs-Cuxart J, Barlet-Ros P, Duffield N, Kompella R.Cuckoo sampling: Robust collection of flow aggregates under a fixed memory budget[C].In: Proc.of the 31st Annual IEEE Int’l Conf.on Computer Communications(Mini-Conf.).Orlando: IEEE, 2012.2751-2755.

[3]程光,唐永宁.基于近似方法的抽样报文流数估计算法[J].软件学报,2013,24(2):255-265.

[4]Hu CC, Liu B, Wang S, Tian J, Cheng Y, Chen Y.ANLS:Adaptive non-linear sampling method for accurate flow size measurement.IEEE Trans.on Communications[J],2012,60(3):789-798..

[5]吴桦,龚俭,杨望.一种基于双重Counter Bloom Filter的长流识别算法[J].软件学报, 2010,21(5):1115-1126.

[6]Zhang Y, Fang BX, Zhang YZ.Identifying heavy hitters in high-speed network monitoring.SCIENTIA SINICA Informationis[J].2010,53(3):659-676.