水平井“多段分簇”压裂簇间干扰的数值模拟
2014-10-20潘林华张士诚程礼军陆朝晖柳凯誉
潘林华 张士诚 程礼军 陆朝晖 柳凯誉
1.国土资源部页岩气资源勘查重点实验室·重庆地质矿产研究院
2.重庆市页岩气资源与勘查工程技术研究中心·重庆地质矿产研究院
3.油气资源与探测国家重点实验室·重庆页岩气研究中心
4.中国石油大学(北京)石油工程学院 5.中国石油长城钻探公司井下作业分公司
水平井分段压裂已经成为低渗透油气藏开发的关键技术[1],常规水平井压裂一般采用单簇射孔、多段压裂的施工模式,形成的压裂裂缝体积有限。国内外学者在常规的水平井压裂的基础上,对压裂工具和压裂工艺进行改进,形成了水平井“多段分簇”压裂方法,每个压裂段射多簇孔,每段能形成多条压裂裂缝,这样能尽可能增加改造体积[2-4],保证低渗透油气藏和非常规油气藏的压裂增产效果。
水平井分段压裂方面,目前主要集中在压裂裂缝条数、裂缝长度和裂缝间距对水平井产能的影响[5-10]。但是,在水平井“多段分簇”压裂过程中,压裂裂缝间的相互干扰是一个无法回避的问题,裂缝干扰的存在可能导致中间的射孔簇无法形成有效的压裂裂缝[11-13]。
笔者基于流—固耦合的基本方程和损伤力学原理,建立了水平井“多段分簇”压裂的三维有限元模型,利用该模型研究了储层物性、施工参数、射孔簇数等对水平井“多段分簇”压裂裂缝干扰的影响。利用所建立的模型对西南某区块的一口水平井进行了压裂设计优化,优化后压裂井的产量增加明显,表明本模型对现场压裂具有指导和借鉴意义。
1 水平井“多段分簇”压裂裂缝扩展数学模型
水平井“多段分簇”压裂,从力学方面分析,可以分成以下3个流场[13]:①液体流场——压裂液在裂缝中的流动,对裂缝面产生应力、应变的影响;②岩石应力场——储层基质承受一定的应力并产生应变;③孔隙中渗流场——孔隙中充满流体,在压裂过程中会发生流动和交换,反过来会影响储层基质的应力和应变。水平井“多段分簇”压裂裂缝干扰主要通过这3个流场的变化而产生。
1.1 流—固耦合基本方程
储层基质的应力遵循有效应力原理为:

根据虚功原理,压裂储层岩石的平衡方程为[14]:
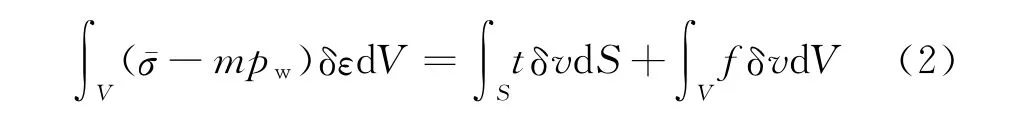
式中δε为储层基质的虚应变率,s-1;t为单元面载荷,N/m2;δv为储层基质的虚运动速度,m/s;f为体力载荷,N/m3;dS为面载荷的作用面积,m2;dV 为计算单元的体积,m3。
根据流体质量守恒原理,流体介质的连续性方程为[14]:

式中J为储层孔隙的体积改变率,无因次;nw为孔隙中液体体积与储层总体积的比值,无因次;ρw为储层液体密度,kg/m3;x为液体流动的方向向量,m;dt为时间步,s;vw为储层液体的流动速度,m/s。
孔隙液体流动速度的计算公式为[15]:
式中a为单位转换常量;g为重力加速度,m/s2;μ为孔隙液体黏度,Pa·s;K 为储层的动态渗透率,mD;pw为储层孔隙压力增量,Pa。
储层的孔隙压力和应力相互耦合,储层孔隙压力和有效应力的变化对孔隙度和渗透率产生影响。本计算模型中,孔隙度和渗透率在计算过程中动态变化,变化方式如下所示[16]:

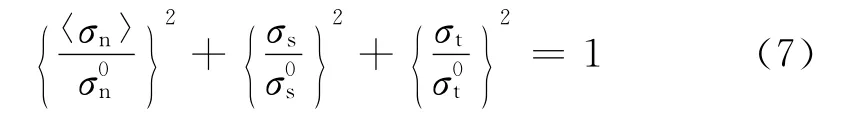
式中σn为垂直于黏结单元的法向应力,Pa;符号〈〉表示黏结单元不抗压;σs、σt分别为平行于黏结单元的两个切向应力,Pa;σ0n为黏结单元的法向损伤极值,Pa;σ0s、σ0t分别为黏结单元的切向损伤的极值,Pa。
裂缝扩展过程中,裂缝扩展造成黏结单元的损伤采用弹性模量线性退化准则:

式中E0为储层的初始弹性模量,Pa;E为储层的动态弹性模量,Pa;d为裂缝扩展造成的损伤因子,无因次,根据裂缝的位移计算获得。
式中φ为储层的动态孔隙度,无因次;φ0为储层的初始孔隙度,无因次;εv为计算单元的体积应变,无因次;K0为岩石的初始渗透率,mD。
1.2 裂缝扩展模型
采用零厚度黏结单元模拟水平井“多段分簇”压裂的裂缝扩展过程,利用黏结单元的损伤表征压裂裂缝扩展。
根据张应力和剪切应力的复合判断准则评价裂缝的起裂、扩展,判断准则为[17]:

式中Qt为黏结单元切向流量,m3/s;topen为张开位移,m;Δp为黏结单元间的压差,Pa。
压裂液沿黏结单元表面的法向流量[19]:

式中Qn为黏结单元的法向流量,m3/s;cn为压裂液的滤失系数,m3/(Pa·s);pb为黏结单元相邻的基质单元的孔隙压力,Pa;pi为黏结单元流压,Pa。
模拟过程中,将混合支撑剂和压裂液的携砂液等效为一种流体,液体等效黏度与支撑剂浓度关系为[20]:

压裂液流动分解为切向流动和法向流动。压裂液沿水力裂缝单元切向流动的计算公式为[18]:
式中μ为等效后的液体的黏度,Pa·s;μ0为无支撑剂的液体黏度,Pa·s;c为携砂液中支撑剂的体积浓度,无因次。
2 水平井“多段分簇”压裂裂缝扩展计算模型
根据西南某地区的部分压裂井的微地震监测和测井解释结果,发现该区块的天然裂缝不发育,压裂过程中,压裂裂缝以平面裂缝为主,因此,本计算模型假设压裂裂缝为平面缝。
所建立的计算模型示意图如图1所示,计算模型的总厚度为60.0m,压裂目的层厚度为40.0m,上下隔层的厚度为10.0m,计算模型的宽度为200.0m,长度(压裂裂缝长度方向)为300.0m。
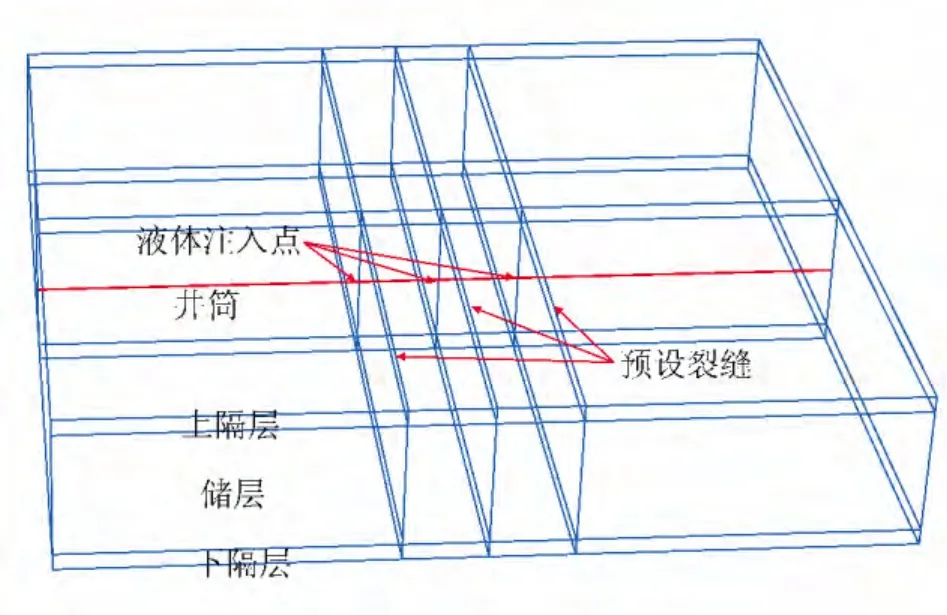
图1 水平井“分段多簇”射孔压裂计算模型示意图
计算模型的参数如表1所示,计算模型主要包括岩石力学、孔隙度、渗透率、地应力、压裂液黏度、施工排量等参数。为了研究某些参数对裂缝干扰的影响,部分参数可能会发生改变。

表1 计算模型参数表
3 模拟结果分析
水平井“分段多簇”压裂过程中,由于采用多簇射孔,每个压裂段可能形成多条压裂裂缝,施工参数、储层参数和射孔簇间距等都会对多裂缝的形成产生影响,如果部分可控参数设置不合理,可能导致部分射孔簇不能开启或不能形成有效的压裂裂缝,从而降低改造体积,减少压裂施工的效率。
利用上述计算模型,主要研究了射孔簇数、射孔簇间距、储层参数、施工参数等对水平井“多段分簇”压裂裂缝干扰规律的影响。
3.1 射孔簇数及簇间距
射孔簇数和簇间距的确定是水平井“多段分簇”压裂设计的核心部分。压裂段长度相同,射孔簇数对压裂裂缝有重要影响,射孔簇数越多,中间的射孔簇越难形成有效压裂裂缝。
笔者模拟了2簇、3簇和4簇射孔在不同的射孔簇间距条件下的裂缝扩展,图2所示为3簇射孔、不同的射孔簇间距条件下的扩展结果,图2-a为射孔簇间距为20.0m时的裂缝扩展结果,中间的射孔簇只能开启小段距离后就发生止裂,不能形成有效裂缝;图2-b所示的为射孔簇间距为26.0m时的裂缝宽度图,中间的射孔簇产生的压裂裂缝能扩展一段距离,但是裂缝的长度有限,不到两端射孔压裂裂缝的一半;图2-c所示的是射孔簇间距为30.0m时的裂缝扩展结果,中间的裂缝长度只比两端的裂缝略短,形成了有效裂缝。
假设中间射孔簇形成的压裂裂缝长度达到两端裂缝的一半以上,认为中间裂缝形成了有效裂缝。不同射孔簇数、簇间距条件下的裂缝扩展情况如图3所示,从图3可以看出:射孔簇数增加,能形成有效裂缝的极限间距增加,且增加幅度较大;射孔簇数为2簇,极限干扰距离为13.0m;射孔簇数增加到4簇,极限干扰距离增加到38.0m。

图2 3簇射孔不同射孔簇间距条件下的裂缝扩展模拟结果图
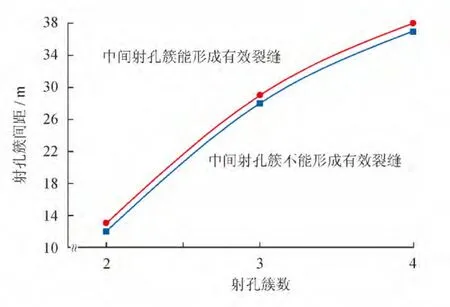
图3 不同射孔簇数和间距条件下裂缝扩展结果图
压裂段的射孔簇数不同,每簇射孔能形成有效裂缝的最小间距与射孔簇数密切相关。射孔簇数越多,中间裂缝能形成有效裂缝的最小射孔簇间距越大,压裂裂缝间的干扰越大,中间的射孔簇越难形成有效裂缝。
3.2 储层参数
储层的弹性模量增大,压裂裂缝宽度降低,这样会降低射孔簇间的干扰,增加中间射孔簇压裂裂缝的长度。图4所示的是3簇射孔、弹性模量为5.5×1010Pa时的裂缝扩展情况,图2-b所示的是3簇射孔、弹性模量为3.5×1010Pa时的裂缝扩展情况,可以发现:储层弹性模量增大2.0×1010Pa时,中间射孔簇的裂缝长度增加了53.0m,中间裂缝形成了有效裂缝。
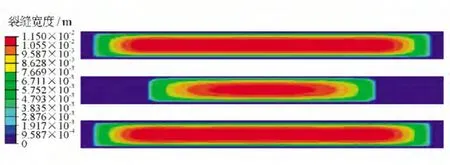
图4 弹性模量为5.5×1010 Pa时,3簇射孔压裂的扩展结果图
弹性模量增大,所有的压裂裂缝的宽度有一定的降低,但是裂缝宽度降低有助于减少裂缝间的干扰,能增加中间射孔簇裂缝的裂缝长度。
储层的抗张强度增加,中间裂缝由于会受到两端裂缝的挤压和干扰,会导致中间裂缝的开启难度增大,这样会加剧射孔簇间的干扰,导致射孔簇间的极限干扰距离增大。
3.3 施工参数
施工排量较大时,压裂裂缝初期的裂缝宽度增加速度较快,会加剧裂缝间的干扰,特别是射孔簇数为4簇时,施工排量的影响尤为明显。
图5所示的是4簇射孔、射孔簇间距为38.0m,施工排量分别为12.0m3/min和16.0m3/min时的裂缝扩展情况,施工排量增大4.0m3/min,中间裂缝的长度发生了明显变化;施工排量为16.0m3/min、4簇射孔条件下,中间射孔簇无法形成有效裂缝。

图5 4簇射孔,不同施工排量下的裂缝扩展结果图
施工排量增大,压裂的初始阶段各射孔簇形成的裂缝的宽度比低排量形成的裂缝的宽度大,这样会加剧裂缝间的干扰,导致中间射孔簇无法形成有效裂缝。
压裂液黏度增加,压裂裂缝的宽度和长度发生变化,但是变化不明显,对水平井“多段分簇”射孔压裂的干扰的影响较小。
4 现场应用
利用所建立的力学模型,对西南某区块的一口水平井的每个压裂段长度和射孔簇间距进行了优化。优化的水平井的储层深度参数如表2所示,水平井在储层1的中下部,离该储层的顶部10.0m,水平井井段长度为1 000.0m。

表2 优化井储层的深度数据表
该水平井的邻井已进行过压裂施工,水平段长为1 000.0m,与将要优化的水平井的水平段长度相同,压裂总计15段,每段长度为66.0m,每个压裂段射3簇孔,射孔簇间距为22.0m,压裂施工后,产量远没有达到设计的预期值,通过对每簇射孔的流量监测发现:大部分压裂段中间的射孔簇几乎没有产量或者产量较小,每个压裂段两端的射孔的产量占总产量的80%以上。产量监测结果证明中间射孔簇没有形成有效的压裂裂缝。
根据改造储层的物性参数以及相邻水平井的压裂施工参数,对要优化的水平井进行了“分段多簇”压裂裂缝扩展模拟,不同射孔簇间距条件下得到的压裂裂缝长度如图6所示(考虑对称性,两端射孔簇的裂缝在图中只画一条曲线):当射孔间距为22.0m时,中间射孔簇的压裂裂缝基本没有压开,只形成了很短的压裂裂缝。当射孔簇间距为30.0m时,中间的射孔簇形成的压裂裂缝和两端射孔簇形成的压裂裂缝基本相当。因此,压裂设计过程中,射孔簇的间距设定在30.0m左右比较合适,根据射孔簇间距参数,每个压裂段的长度确定为90.0m,压裂段数为11段。
压裂施工后,通过对每段射孔簇的产量进行监测发现:每簇中间射孔都有一定的产量,且差别不是很大。压裂过程中减少了4个压裂段,但是,优化后的井的油气总产量比邻井的总产量更高。这样也证明了设计的每簇射孔都形成了比较长的有效裂缝,间接验证了计算模型的正确性和指导性。

图6 不同射孔簇间距条件下的裂缝长度结果图
5 结论
基于流—固耦合的基本方程和损伤力学的基本原理,建立了水平井“多段分簇”压裂裂缝扩展的三维有限元力学模型,利用该模型对水平井“多段分簇”压裂簇间裂缝干扰进行了模拟计算,通过模拟发现:
1)射孔簇数和射孔簇间距是影响水平井“多段分簇”射孔压裂簇间裂缝干扰的主要影响因素。射孔簇数越多,每个压裂段裂缝间的干扰越严重,射孔簇间距越小,裂缝间的干扰越严重。
2)施工参数和储层参数会对裂缝扩展结果产生一定的影响,其中施工排量对4簇射孔的影响较大。
3)利用所建立的计算模型,可以为现场压裂施工确定射孔簇数和射孔簇间距提供一定的指导和借鉴。
[1] 李春芹.水平井分段压裂在特低渗透油藏开发中的应用[J].西南石油大学学报:自然科学版,2011,33(6):85-88.LI Chunqin.Application of horizontal well fracturing technology in thin layer and ultra-low permeability reservoir development[J].Journal of Southwest Petroleum University:Science & Technology Edition,2011,33(6):85-88.
[2] 程远方,李友志,时贤,等.页岩气体积压裂缝网模型分析及应用[J].天然气工业,2013,33(9):53-59.CHENG Yuanfang,LI Youzhi,SHI Xian,et al.Analysis and application of fracture network models of volume fracturing in shale gas reservoirs[J].Natural Gas Industry,2013,33(9):53-59.
[3] 吴奇,胥云,王腾飞,等.增产改造理念的重大变革——体积改造技术概论[J].天然气工业,2011,31(4):7-12.WU Qi,XU Yun,WANG Tengfei,et al.The revolution of reservoir stimulation:An introduction of volume fracturing[J].Natural Gas Industry,2011,31(4):7-12.
[4] 李勇明,彭瑀,王中泽.页岩气压裂增产机理与施工技术分析[J].西南石油大学学报:自然科学版,2013,35(2):90-96.LI Yongming,PENG Yu,WANG Zhongze.Analysis of shale gas fracture stimulation mechanism and operating techniques[J].Journal of Southwest Petroleum University:Science & Technology Edition,2013,35(2):90-96.
[5] 邹雨时,张士诚,马新仿.页岩气藏压裂支撑裂缝的有效性评价[J].天然气工业,2012,32(9):52-55.ZOU Yushi,ZHANG Shicheng,MA Xinfang.Assessment on the effectiveness of propped fractures in the fracturing of shale gas reservoirs[J].Natural Gas Industry,2012,32(9):52-55.
[6] 赵金洲,任岚,胡永全.页岩储层压裂缝成网延伸的受控因素分析[J].西南石油大学学报:自然科学版,2013,35(1):1-9.ZHAO Jinzhou,REN Lan,HU Yongquan.Controlling factors of hydraulic fractures extending into network in shale formations[J].Journal of Southwest Petroleum University:Science & Technology Edition,2013,35(1):1-9.
[7] AYERS K L,AMINIAN K,AMERI S.The impact of multistage fracturing on the production performance of the horizontal wells in shale formations[C]∥paper 161347 presented at the SPE Eastern Regional Meeting,3-5October 2012,Lexington,Kentucky,USA.New York:SPE,2012.
[8] 郭肖,杜志敏.非均质性对水平井产能的影响[J].石油勘探与开发,2004,31(1):91-93.GUO Xiao,DU Zhimin.Impacts of permeability heterogeneity on horizontal well productivity[J].Petroleum Exploration and Development,2004,31(1):91-93.
[9] 曾凡辉,郭建春,何颂根,等.致密砂岩气藏压裂水平井裂缝参数的优化[J].天然气工业,2012,32(11):54-58.ZENG Fanhui,GUO Jianchun,HE Songgen,et al.Optimization of fracture parameters of fractured horizontal wells in tight sandstone gas reservoirs[J].Natural Gas Industry,2012,32(11):54-58.
[10] WONG S W,GEILIKMAN M,XU G S.Interaction of multiple hydraulic fractures in horizontal wells[C]∥paper 163982presented at the SPE Middle East Unconventional Gas Conference and Exhibition,28-30January 2013,Muscat,Oman.New York:SPE,2013.
[11] 赵金洲,王松,李勇明.页岩气藏压裂改造难点与技术关键[J].天然气工业,2012,32(4):46-49.ZHAO Jinzhou,WANG Song,LI Yongming.Difficulties and key techniques in the fracturing treatment of shale gas reservoirs[J].Natural Gas Industry,2012,32(4):46-49.
[12] 胡永全,贾锁刚,赵金洲,等.缝网压裂控制条件研究[J].西南石油大学学报:自然科学版,2013,35(4):126-132.HU Yongquan,JIA Suogang,ZHAO Jinzhou,et al.Study on controlling conditions in network hydraulic fracturing[J].Journal of Southwest Petroleum University:Science & Technology Edition,2013,35(4):126-132.
[13] 彪仿俊,刘合,张士诚,等.水力压裂水平裂缝影响参数的数值模拟研究[J].工程力学,2011,28(10):228-235.BIAO Fangjun,LIU He,ZHANG Shicheng,et al.A numerical study of parameter influences on horizontal hydraulic fracture[J].Engineering Mechanics,2011,28(10):228-235.
[14] ZIENKIEWICZ O C,TAYLOR R L.The finite element method:An introduction with partial differential equations[M].Burlington:Elsevier,2005:42-45.
[15] 董平川,徐小荷.储层流固耦合的数学模型及其有限元方程[J].石油学报,1998,19(1):64-70.DONG Pingchuan,XU Xiaohe.The fully coupled mathematical model of the fluid-solid in an oil reservoir and its finite element equations[J].Acta Petrolei Sinica,1998,19(1):64-70.
[16] 冉启全,李士伦.流固耦合油藏数值模拟中物性参数动态模型研究[J].石油勘探与开发,1997,24(3):61-65.RAN Qiquan,LI Shilun.Study on dynamic models of reservoir parameters in the coupled simulation of multiphase flow and reservoir deformation[J].Petroleum Exploration and Development,1997,24(3):61-65.
[17] ADACHI J,SIEBRITS E,PERICE A.Computer simulation of hydraulic fractures[J].International Journal of Rock Mechanics & Mining Sciences,2007,44(5):739-757.
[18] CAMANHO P P,DAVILA C G.Mixed-mode decohesion finite elements for the simulation of delamination in composite materials[R].NASA/TM-2002-211737,Hampton,Virginia:Langley Research Center,2002:1-37.
[19] 李宗利,王亚红,任青文.自然营造力作用下岩石单裂纹水力劈裂数值仿真模型[J].岩石力学与工程学报,2007,26(4):727-733.LI Zongli,WANG Yahong,REN Qingwen.Numerical simulation model of hydraulic fracturing of rock with a single fracture under natural hydraulic power[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(4):727-733.
[20] 张广明,刘合,张劲.油井水力压裂流—固耦合非线性有限元数值模拟[J].石油学报,2009,30(1):113-116.ZHANG Guangming,LIU He,ZHANG Jin.Simulation of hydraulic fracturing of oil well based on fluid-solid coupling equation and non-linear finite element[J].Acta Petrolei Sinica,2009,30(1):113-116.
