波罗的海干散货运价指数的马尔可夫链分析
2014-10-18毕艳芳
毕艳芳
(上海海事大学经济管理学院,上海201306)
一、引言
波罗的海干散货指数(BDI)是投资者研究航运股的重要工具,干散货航运上市公司的股价走势与BDI紧密相关。波罗的海干散货市场运价指数即BDI,一直被认为是反映国际干散货运输市场变化的晴雨表,同时是初级商品市场价格走势的风向标。研究BDI的波动规律,对其发展趋势进行预测得到人们广泛的关注。吕靖(2002)通过对波罗的海国际干散货运价指数分别提取长期趋势项、周期波动项和季节波动项以后,建立ARMA模型,对 BFI(BDI的前身)进行了短期预测[1];徐萍(2005)采用小波分析和神经网络对BFI进行了预测研究[2];刘晶,卢春霞(2008)结合FFA市场,建立了波罗的海干散货运价指数ARMA预测模型[3];聂金龙,李序颖(2009)引入ARFIMA模型,来改进传统的ARMA预测模型[4];靳廉洁(2010)针对巴拿马型干散货船舶,进行基于支持向量机(SVM)模型的波罗的海运价指数预测研究[5];魏文臻杰,李序颖(2011)通过引入波罗的海原油运价指数BDTI这一外生变量,提出了一种ARMAX模型的短期 BDI预测方法[6]。
本文将引入马尔可夫链理论,建立BDI的马尔可夫预测模型,并据此分析BDI的短期波动变化趋势可能性[7]。
二、数学理论
1.马尔可夫链的定义
将具有“过去只影响现在,而不影响将来”特点的随机过程成为马尔可夫过程。状态离散的马尔可夫过程称为马尔可夫链。符合马氏性的随机数列可用马尔可夫链进行状态预测。
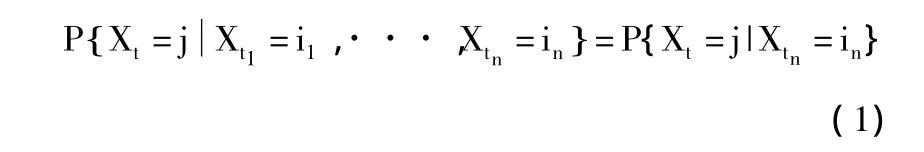
则称{Xn:n≥0}为马尔可夫链,简称马氏链。
随机过程Xn:n≥{}0是马氏链的充要条件是,对于任意的 n≥1,及任意的 i1,i2,···,in,j∈S,有
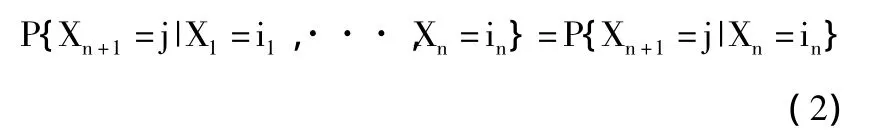
2.转移概率
对于 马 氏 链{Xn:n≥0},称P(ijn)(m)=PS为系统在时刻m时处于状态i的条件下,经过n步转移到状态j的n步转移概率。P(ijn)(m)具有以下性质:
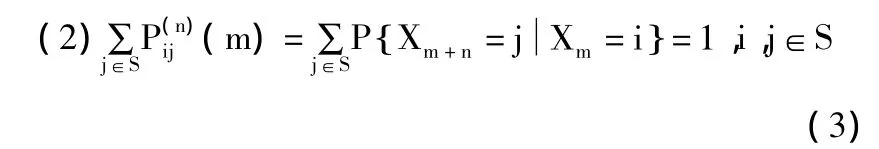
对于齐次的马氏链Xn:n≥{}0,有
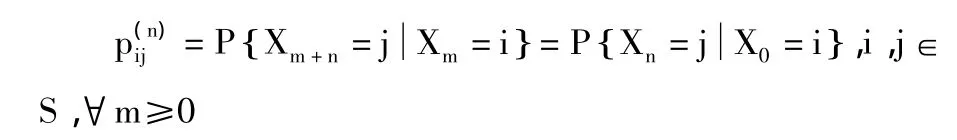
转移概率矩阵形式为

P满足:(1)所有元素非负,(2)各行元素之和为1。
3.马氏性的检验
检验随机过程是否具有马氏性,是应用马尔可夫链模型进行数据分析的首要前提。通常对于离散型的马尔可夫链是用χ2统计量来检验:
为了说明我们引入频数矩阵(nij)n×n,nij是系统从状态i转移到j状态的次数。
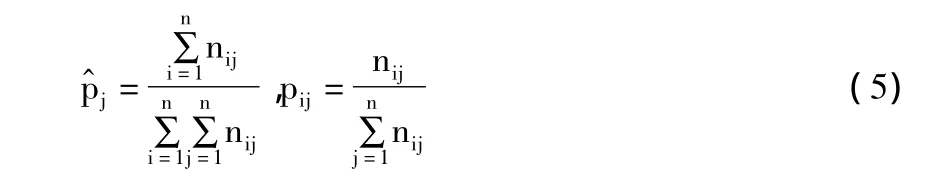
则统计量
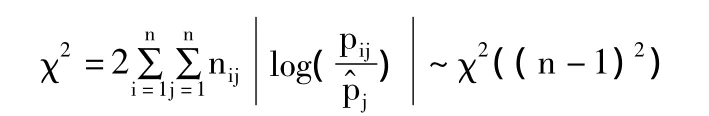
4.C-K方程
对于齐次马氏链{Xn:n≥0}的n步转移概率,有
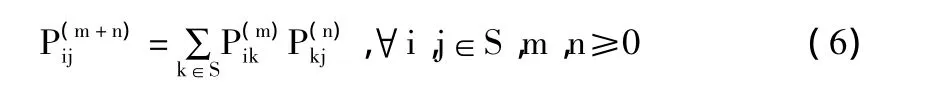
即为C-K方程,在马尔可夫链转移概率计算中起着重要作用。写成矩阵形式即:P(m+n)=P(m)P(n),且P(n)=Pn。所以对齐次马尔可夫链来说,一步转移概率Pij就可以确定所有的n步转移概率,即
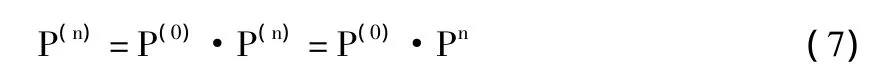
这对于应用马尔可夫链来进行预测有关键意义。
二、马尔可夫链分析模型的建立
1.数据选取与状态划分
波罗的海干散货运价指数BDI随着时间而不断变化,形成时间序列数据。这里选取2013年12月2日至2014年3月5日的BDI数据(来源Clarkson SIN数据)。
因为BDI一直被认为是反映国际干散货运输市场变化的晴雨表,也为简化分析,将状态划分为“上涨”“持平”“下跌”三种状态[8],具体划分法如下:
(1)将BDI数据进行差分处理;
(2)状态划分标准:指数上涨超过20点,为状态1,称为“上涨”;指数上涨或者下跌在20点范围内,为状态2,称为“持平”;指数下跌超过20点,为状态3,称之为“下跌”。故状态空间S=1,2,{}3。
(3)据上述标准进行状态划分,得到如下结果(见表1).
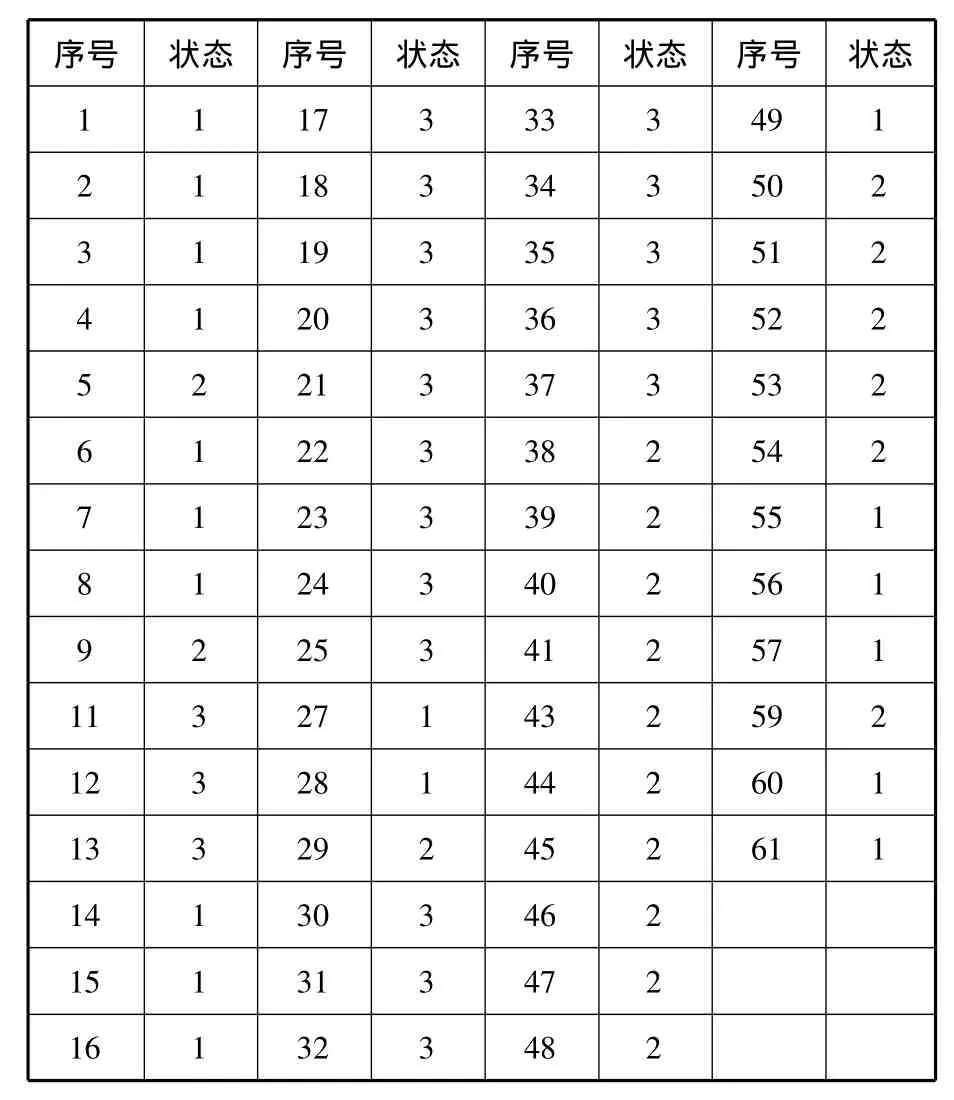
表1 2013年12月2日至2014年3月5日的BDI情况
2.检验马尔科夫性
用nij表示BDI从状态i转移到j状态的次数,通过计算得到频数矩阵(nij)n×n:
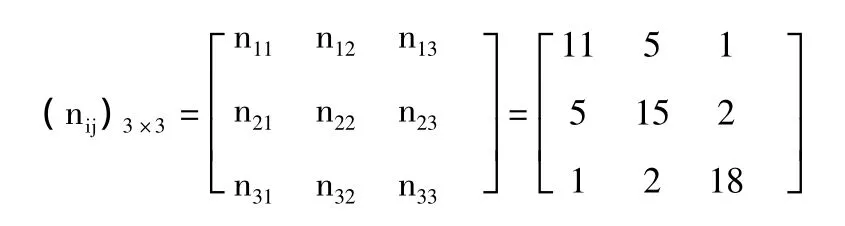
将频数矩阵的第j列之和除以各行各列的总和,由公式(5)得到,并计算得到
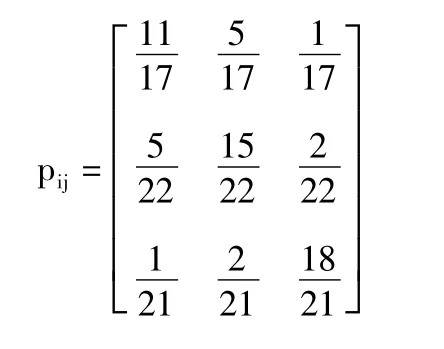
由公式计算得到χ2=60.44257,取α=0.05,查表得χ2(3-1)=5.991,所以此过程是马氏链过程,具有马氏性[9]。
3.转移概率矩阵计算
由表1可知,最后一天的状态为1,而没有出现状态转移,故出现状态1的次数为18-1=17次,其中由状态1转1的次数为11次,即转移概率;状态1转2的次数为5次,即转移概率;状态1转3的次数为1次,即转移概率同理可计算得到
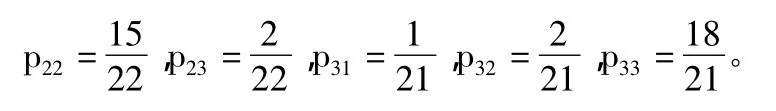
由此可得,该BDI状态的一步转移概率矩阵:

因此利用表1资料预测以后交易日的情况,由于马氏性和齐次性,我们用第61个交易日的状态为初始状态,由表1可知,2014年3月5日的数据落在状态1区间内,即初始分布为P(0)=(1 0 0 ),利用模型(7)式,可计算得第62个交易日的BDI状态概率情况:
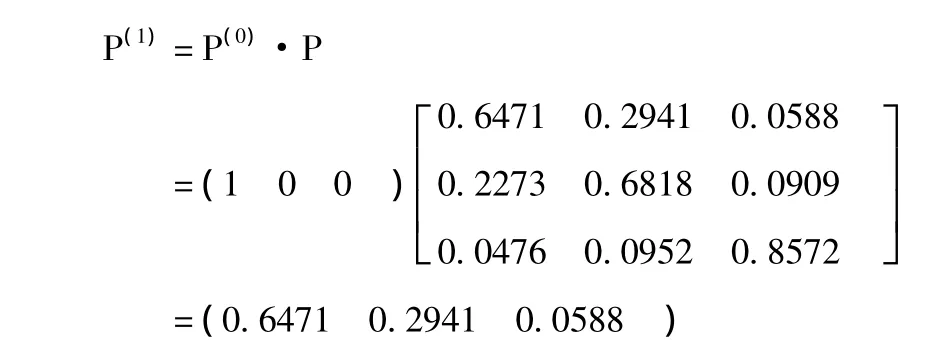
经计算表明,第62个交易日的BDI指数上涨超过20个点的概率为64.71%,指数变动在-20到20范围内的概率为29.41%,指数下降超过20个点的概率为5.88%。
第59个交易日的BDI状态概率情况:

第60个交易日的BDI状态概率情况:
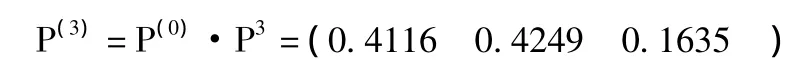
第60个交易日的BDI状态概率情况:

这样,只要稳定条件不变,即一步转移概率不变,以后各个交易日的状态都可预测分析[10]。
三、马尔可夫链分析结果说明
据以上分析可知,随着交易日的增加,BDI指数上涨超过20点的可能性在不断下降,其他两个状态出现的可能性在上升,这与现实情况一致。越远期越是难预测,出现三种状态的可能性将会差不多。同时,需要说明的是,BDI指数除了受市场因素影响之外,还会受到其他很多外界因素的影响,不能保证转移概率矩阵不变,因此本方法适宜于对BDI进行短期预测分析,为波罗的海干散货运价指数的科学预测提供新的思路。
[1] 吕靖.海运价格指数的波动规律[J] .大连海事大学学报,2003(2).
[2] 徐萍.基于小波分析和神经网络的BFI预测研究[D] .大连海事大学,2005.
[3] 刘晶,卢春霞.波罗的海干散货运价指数预测模型分析[J] .航海技术,2008(5).
[4] 聂金龙,李序颖.波罗的海干散货运价指数的ARFIMA模型研究[J] .中国水运,2009(4).
[5] 靳廉洁.基于支持向量机的干散货运价指数预测研究[D] .大连海事大学,2010(6).
[6] 魏文臻杰,李序颖.基于ARMAX模型的短期BDI预测[J] .物流工程与管理,2012(1).
[7] 李龙锁 .随机过程[M] .北京;科学出版社,2011.
[8] 韦丁源.股市大盘指数的马尔科夫链预测法[J] .广西广播电视大学学报,2008(9).
[9] 叶宗文.股票价格的马氏链预测法[J] .重庆师范大学学报,2006(3).
[10] 孟银凤,李荣华.股票价格的马氏链预测模型[J] .数学理论与应用,2010(9).
