旋转翼型冲击水介质动态模拟研究

孙兰凤，张成波

● （1.四川电力职业技术学院 动力工程系，四川成都 610071；2.东方电气股份有限公司，四川成都 610036）

旋转翼型冲击水介质动态模拟研究

孙兰凤1，张成波2

● （1.四川电力职业技术学院 动力工程系，四川成都 610071；2.东方电气股份有限公司，四川成都 610036）

简要介绍了旋转翼型声辐射的研究现状，建立了NACA系列翼型以及环形水域模型。对翼型采取刚性体，对水介质采用 Gruneisen状态方程来定义材料的压力，对模型采用 8节点实体单元进行网格划分。采用ALE算法模拟了水域单元的声压值，尤其是翼型在同一起始和终止时间的速度—时间曲线(直线、正弦线、抛物线以及正切线)被研究了。对同一单元在不同旋转方式下的声压值以及同一旋转方式下不同单元的声压值进行了比较。

翼型；冲击；动态模拟

0 引言

翼型是工程技术领域常用的典型形体，在水利水电工程、航空、动力工程等许多技术部门都有广泛的应用[1]。

近年来，旋转翼型的声辐射研究受到了极大关注。许多学者在实验和理论方面首先对振动翼型的流场进行了测量。文献[2]引用了Anderson论文中对振动翼非定常流问题的研究，对翼型流场进行了显示实验。动态失速问题研究也就是前缘涡分离问题研究以及在推进方面对翼型最优运动方式研究，同时完成了振动翼型全面的推进能力和效率的测量。文献[3]运用Rankine奇点一阶面元法，以在无限水域中斜航运动的舵为研究对象，考虑线性自由表面边界条件计算了穿透自由表面定常斜航运动物体的水动力。文献[4]主要讨论了自由液面下三维水翼定常升力绕流的水动力系数计算问题。文献[5]运用有限体积法结合双时间推进技术求解三维非定常欧拉方程，模拟了有限翼展机翼在同时具有上下拍动和俯仰运动状态下的非定常流场，计算了不同状态下扑翼的升力及推力，分析了各个影响因素对扑翼气动特性的影响。文献[6]运用有限体积法结合双时间推进技术数值求解三维非定常Euler方程，模拟了机翼在运动状态下的非定常流场，采用双时间推进法求解非定常Euler方程，验证此方法可以极大地提高非定常流场计算效率。同时，刘晓宙[7-10]在余志兴[11-12]研究粘性流场结果的基础上，对流体通过涡激振动机翼的声辐射进行了研究，首先考虑了机翼的强迫转动，只有一个自由度，进而考虑了更为复杂机翼振动，有两个自由度，分别是上下振动和绕弹性中心的转动，得出流体绕涡激振动的机翼引起的声辐射大于流体绕固定机翼引起的声辐射，特别是当涡脱频率和机翼的固有的振动频率一致时，声辐射达到最大，并且根据翼型的周期性涡发放，需要较大的攻角，而攻角的具体大小与翼型有关系，提出了可以利用改变翼型形状控制涡激噪声的可能性。

对流体与翼型相互作用产生声辐射的问题，大部分按照流噪声的思路在研究。对于运动翼型，文献[7-8，10-12]也只是考虑了翼型转动角度按照正弦曲线变化的情况，在潜艇实际航行过程中，辐射噪声的极值点常出现在舵叶开始加速转动的过程中。为了研究旋转翼型从静止状态加速旋转至一定角度的过程中声辐射的特性，本文采用了翼型冲击水介质模型，分别选取适当的材料模拟了刚性的翼型在旋转过程中对周围静止水域的冲击作用，研究了旋转方式对水域压力的变化的影响，从而得到了旋转翼型冲击水介质的特性以及声辐射的规律。

1 翼型与水域模型

为了准确的表达翼型，采取工程中常用的NACA系列翼型。针对翼型的旋转运动方式，在水域模型上采取了环形水域，一方面便于计算时划分网格，另一方面在察看结果时便于选取观测点进行对比分析。图1、2分别给出了建立的翼型模型以及水域模型。

图1 舵叶壳体翼型模型

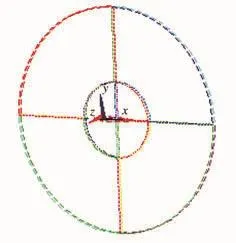
图2 水域模型

1.1 模型单元

翼型和水域模型由8节点单元划分。单元在每个节点在x，y，z方向都具有位移、速度以及加速度。单元默认一个节点进行粘性沙漏控制来加快单元变形，这样可以节省计算时间以及在大变形的时候不会产生单元失效。翼型和水域单元见图3。

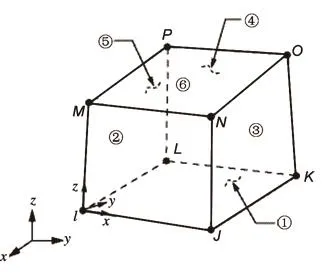
图3 翼型和水域单元

2 材料选择

2.1 舵叶壳体的材料模型

在材料选择方面，因为研究的侧重点是翼型冲击水介质，目的是为了得到水域压力的变化，因此翼型采用刚性体，假设翼型在旋转过程中未产生自身的颤振，并且在与水介质作用过程中，不发生变形。

用刚体来定义模型中较硬的部分能够大大减少显示动力分析的计算时间，刚体将自由度耦合在质心，因此无论有多少个节点，但各刚体只有6个自由度。质量、质心和惯性矩将根据刚体的体积与单元密度自动计算。作用在刚体上的力与力矩在每个时间步由各节点值相加而成。刚体的运动首先在质心处计算，然后转换到各个节点上，并且刚体不需要网格连续。尤其是要计算接触刚度，刚体材料参数值要用实际值。

在计算时，初步定义了翼型密度DENS为7800kg/m3，弹性模量为200GPa，泊松比为0.3，先不考虑翼型直线运动，对翼型各个坐标方向的运动进行约束；并且在翼型旋转方面，只考虑翼型绕某一坐标轴转动。

2.2 水介质的材料选择

在分析中，假设水介质是可压缩的，采用格林纳森(Gruneisen)状态方程定义压力体积的关系，确定材料是压缩的。

2.2.1 水介质的材料状态方程

具有立体撞击速度—粒子的速度状态Gruneisen方程定义压缩材料的压力为：

Gruneisen方程是一种绝热熵增的状态方程，通常利用测量冲击波波速—波后质点粒子速度曲线（又叫us-up曲线）来决定方程的参数，us-up曲线中s为震动；p为粒子；该曲线采用S1、S2、S3三个系数多项式拟合，是us-up曲线的斜率系数；C是粒子速度为0时的波速，即曲线在y轴的截距；γ0是Gruneisen参数；a是对γ0的修正系数；E是初始内能，常温下通常设为0；V是初始相对体积，即相对没有任何变形的体积，初始无体积应变时则设为1；根据相对体积V，压缩量μ定义为：μ=(1/V)-1。

2.2.2 水介质材料模型设定

水介质材料状态方程不用计算偏应力，也可以选择定义粘度。在计算时，初步定义水密度DENS为1000kg/ m3，水中声速C为1647m/s；us-up曲线的斜率系数S1=1.921，S2=-0.096，S3=0；Gruneisen参数γ0=0.35，并且初始内能E=0，相对体积V=1。

3 计算方法

3.1 计算方法的讨论比较

在翼型与水介质作用过程中，由于翼型运动有空间相对较大的位移并且在实际情况中，水介质和翼型间有物质输送。如果翼型周围环绕流体介质的单元基于 Lagrange型单元时，就会产生严重的变形，直接导致每次迭代计算时的时间步长变得很小，因此模型的计算时间变得很长。另外，由于计算网格的畸变，可能直接影响到数值计算的精度。Euler型的有限元模拟虽然提高了在固定网格上采用Navier-Stokes方程时间解的精度，同时也增加了计算的时间。所以，选择ALE算法来进行分析。

ALE方法最初出现于数值模拟流体动力学问题的有限差分方法中。这种方法兼具Lagrange方法和Euler方法二者的特长，即首先在结构边界运动的处理上引进Lagrange方法的特点，因此能够有效地跟踪物质结构边界的运动；其次在内部网格的划分上，吸收了Euler的长处，也就是使内部网格单元独立于物质实体而存在，但它又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变。这种方法在分析大变形问题时是非常有利的。使用这种方法时网格与网格之间物质也是可以流动的。

3.2 分析时间及时间积分

考虑阻尼影响的运动方程为：

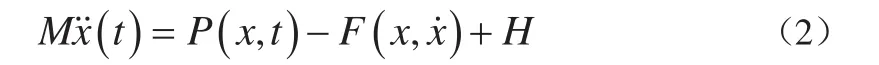
时间积分采用显式中心差分格式，其算式为：

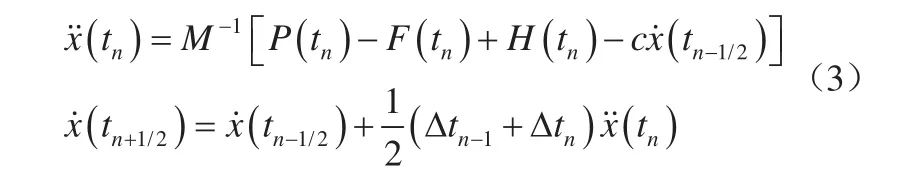
由于采用集中质量矩阵M，运动方程（3）的求解是非偶合的，不需要组集成总体积矩阵，因此大大节省了计算时间。但是显式中心差分法是有条件稳定的。模拟时采用变时不常增量解法。每一时刻的时步长由当前构形的稳定性条件控制，其算法为：

线计算每一个单元的极限时步长Δtei，i=1，2… (显式中心差分法稳定性条件允许的最大时步长)则下一步长取其极小值，即：

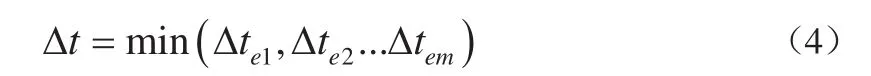
式中，Δtei为第i个单元的极限时步长；m是单元数目。

对于舵叶壳体模型和水域模型所选择的三维实体单元：

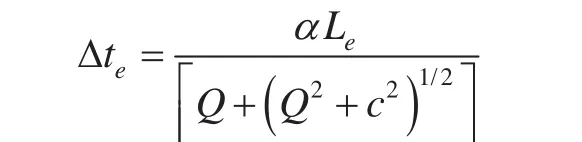
本文设定的翼型转动的最低速度为3º/s。为了满足最低的要求，假设在1s的时间内，舵叶旋转的极值速度为0.0523598rad/s。

4 对不同运动曲线的动态模拟

4.1 动态模拟速度曲线

本文对不同的已知曲线进行了模拟。在模拟曲线的选择中，参考了典型的电梯曲线的组成，选择了直线，正弦曲线，抛物线以及正切线进行分析。

首先，对于直线速度时间曲线，选取V=0.0523598t(0≤t≤1s)。其次选取正弦速度时间曲线为：

V=0.0523598sin (πt/2) (0≤t≤1s)。

最后分别选取抛物线速度时间曲线及正切速度时间曲线为：

V= 0.0523598t2(0≤t≤1s)及V=0.0523598tan(πt/4)。

根据上述分析，选取相同的水域单元进行对比，见图4。

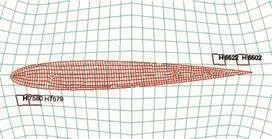
图4 部分水域中的舵叶模型

4.2 提取计算结果

采取相同的模型和计算方法，仅改变翼型在相同的时间内达到相同的极值速度时采用的速度曲线，分别得到不同的曲线下观测点的压力值，如图5所示。

对某一水域单元进行进一步的对比分析，不同时刻，不同的舵叶壳体旋转速度曲线在此单元产生的压力值如图6所示。

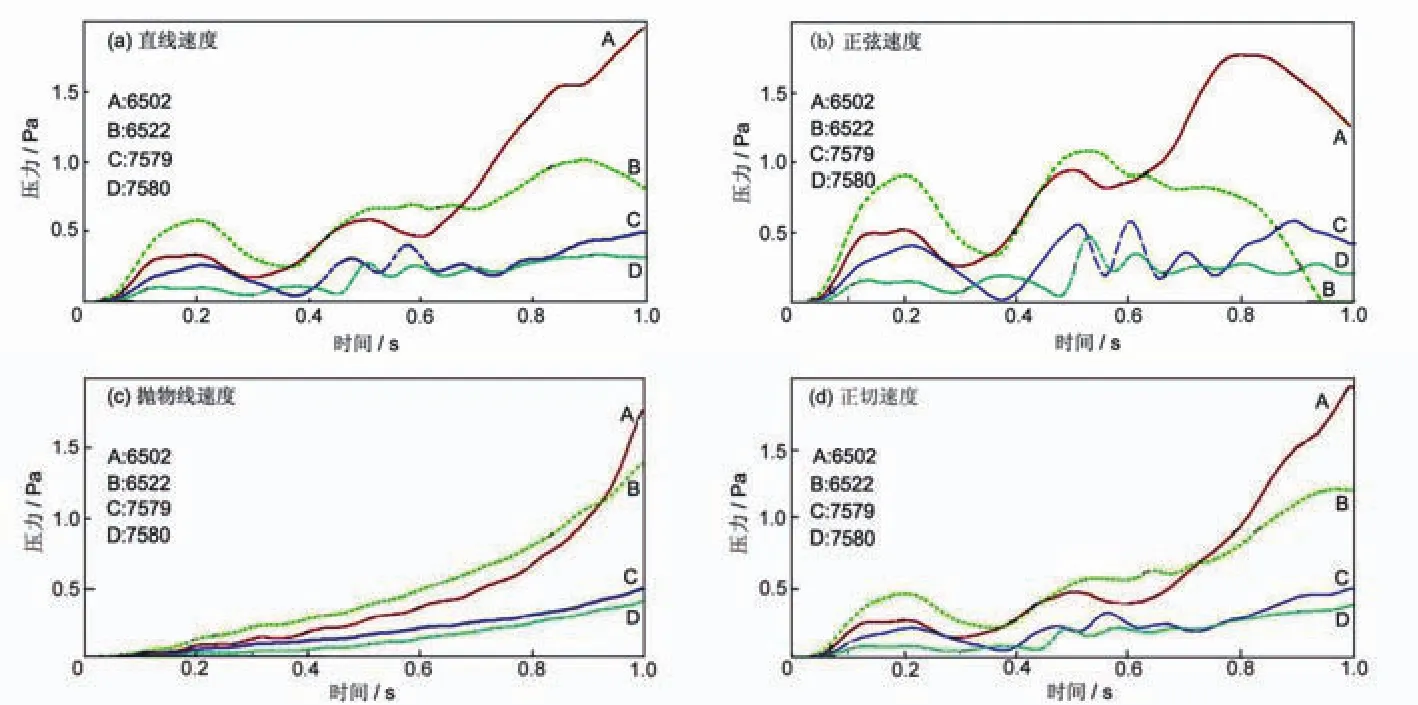
图5 不同速度曲线的单元压力

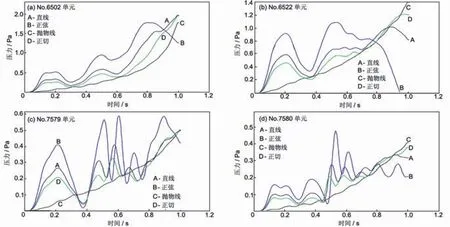
图6 不同单元的压力

5 结果分析及讨论

在同一速度曲线的模拟过程下，尾缘处观测点6502，6522处的声压明显大于前缘处观测点7579，7580处声压。对于直线速度时间曲线，尾缘观测点 6502和 6522在t＜0.664287s时，6522处声压总是大于 6502处，而在t≥0.664287s时，6522处声压转变为小于6502处声压，而对于正弦速度时间曲线，此分界时间点在t=0.626316s处，对于抛物线速度时间曲线，分界时间点在t=0.093956s处，正切线速度时间曲线，分界时间点在t=0.730527s。这表明在对翼型旋转搅动水介质的声压研究中，可以直接选取尾缘观测点，根据尾缘处声压值的比较和声压值变化的分界时间点，在分界时间的前段可选择尾缘内侧水域作为分析对象（如水域单元 6522），在分界时间的后段可选择外侧水域作为分析对象（如水域单元6502）。

对不同的速度曲线下的同一观测点，抛物线速度曲线在翼型初始启动时刻的声压最小，对于尾缘6502处，一直到t≥0.929066s后，才有正弦速度时间曲线下的此处声压最小。尾缘6522处，在t≥0.333159s后，正切速度时间曲线下的声压才小于抛物线速度时间曲线下的声压，并且正切曲线下的声压并未持续降低，在t≥0.408957s后，抛物线下的此点声压最小，最后在t≥0.777732s后，才有正弦速度时间曲线下的此处声压最小。这表明在翼型旋转初始时刻，采用抛物线速度时间曲线可降低水域声压值，在翼型旋转速度到达极值的末端时刻，采用正弦速度时间曲线可降低水域声压值，可供设计水下翼型旋转的声学设计做参考。

[1]夏国泽.船舶流体力学[M].武汉:华中科技大学出版社,2003.

[2]王肇.二维振动机翼的流场测量及数值分析[D].长沙:中国科学技术大学,2004.

[3]汪淳.穿透自由表面倾侧舵的水动力计算[D].武汉:武汉理工大学,1999.

[4]刘华.三维水翼水动力数值计算[D].武汉:华中科技大学,2003.

[5]龚凯.有限翼展扑动翼的欧拉方程数值模拟[D].西安:西北工业大学,2003.

[6]周成刚.运动机翼流场的欧拉方程求解[D].西安:西北工业大学,2002.

[7]刘晓宙,缪国平,余志兴,等.流体通过二维振动翼型的声辐射研究[J].声学学报,2004,l29(2):122-130.

[8]刘晓宙,缪国平,余志兴,等.流体通过涡激振动机翼的声辐射研究[J].声学学报,2005,30(1):56-62.

[9]刘晓宙,缪国平,唐春权,等.粘性流体通过二维振荡圆柱的声辐射研究[J].船舶力学,2002,6(4):75-88.

[10]刘晓宙.旋涡运动与涡激噪声的研究[D].上海:上海交通大学,2000.

[11]余志兴,刘应中,缪国平.二维机翼弹簧系统的涡激振动[J].船舶力学,2002,6(5):25-32.

[12]余志兴.粘性流场中的水弹性计算[D].上海:上海交通大学,1999.

Dynamic Simulation Study on Rotating Aerofoil Impacting Water Medium

SUN Lan-feng1,ZHANG Cheng-bo2
(1.Department of Power Engineering,Sichuan Electric Vocational and Technical College,Chengdu 610071,China; 2.Dongfang Electric Corporation,Chengdu 610036,China)

The present state of study on the sound radiation of rotating aerofoil is simply introduced.The models of NACA series aerofoil and annular fluid are built.The rigid material is adopted in aerofoil and the Gruneisen equation of state is used to define the pressure of the water medium,both models is meshed by eight nodes solid elements.The sound pressure of the water unit is simulated by using ALE algorithm.In particular,four different velocity-time curves with the same starting and ending time and velocity of aerofoil movement (straight line,sine curve,parabolic curve,tangent curve) are developed.The different kinds of sound pressure of the same element with different rotating style and the different elements with the same rotating style are compared with each other.

aerofoil; impact; dynamic simulation

TP391.9;TK733.3

A

孙兰凤（1978-），女，讲师，研究生，主要研究方向为流体机械及工程。