基于状态反馈控制的逆变器电流控制器的设计

柏祥华，徐 琛

· （海军驻南京地区航天机电系统军事代表室，江苏 南京210006）

基于状态反馈控制的逆变器电流控制器的设计

柏祥华，徐 琛

· （海军驻南京地区航天机电系统军事代表室，江苏 南京210006）

采用传统控制策略对低脉冲逆变装置的交流电流控制器进行设计时，控制器系统带宽通常会接近系统的基波频率，导致系统动态响应变差。提出了一种改进的电流控制策略，通过状态反馈控制的极点配置方法克服了这一难题，从而大大提高线性控制器的增益。电流控制器的设计以离散条件下的线性状态空间设计为原则，可使控制系统的动态响应和稳定性能更加优越，且系统具有更强的鲁棒性。最后，对设计结果进行了仿真。结果表明，基于状态反馈控制规律的极点配置法所设计的电流控制器比传统的PR设计方案具有更好的动态性能。

逆变器控制；电流控制器；状态反馈；极点配置

0 引言

目前以电流作为被控对象的电压型逆变器(CCVSI)广泛应用于电机驱动，电能质量管理和新能源开发利用等方面。如果采用经典线性调节方式来控制CCVSI系统的输出电流，为了实现对输出电压的控制，需要提高控制器的反馈增益[1]，其控制原理框图如图1所示。同时为了减少稳态误差，要求设计的控制器在给定基波频率f0有很大的增益，常用实现方法有PR控制和同步d-q系下的PI控制。在采用这两种控制策略时，都要求闭环带宽尽可能的高，以获得较好的动态响应。然而，为了保证其稳定性，实际系统往往把带宽限制在PWM频率的10%以下。在航空电源中为了降低开关损耗，会将调制波与载波比值设计的很小，结果导致控制系统的动态响应大大降低。而过低的采样频率所带来的信号传输延迟会对系统稳定性产生较大的影响，较高的采样频率虽然提高了闭环系统的带宽，却降低了系统的鲁棒性。

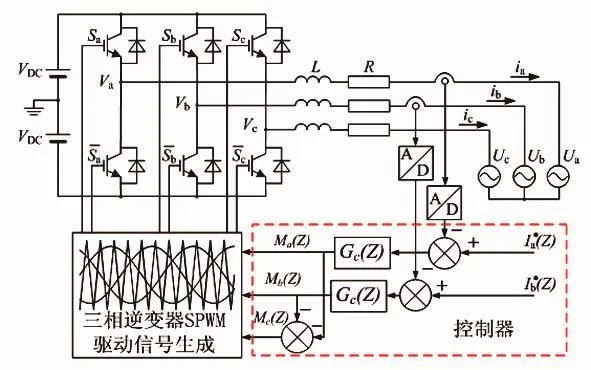
图1 以电流作为被控对象的三相电压型逆变器的典型控制原理框图

基于上述问题，本文提出了一种改进的电流控制策略，以提高线性控制器的增益和获得较好的动态响应。而且，改进的控制器中可以附加系统反馈变量，以此建立状态变量反馈控制去获得较好的控制增益。同时依据这种方法设计的系统在变量变化时，其鲁棒性会大大增强。

1 CCVSI型系统的状态数学模型

在CCVSI型系统控制器设计过程中，首先需要建立系统状态模型。由于逆变器的输出电压平均值与负载电压值两者在稳态工作时是相等的，因此整个三相逆变系统可等效成两个独立且相同的单项电流控制器模型[2]。系统的负载电流i(t)在稳态时为：

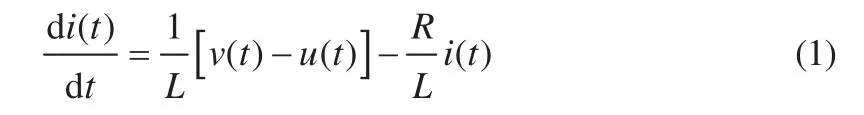
式中：v(t)为三相逆变器桥臂输出电压；u(t)为负载电压值。由于采用数字控制，因此需要将连续时间域下的CCVSI模型转化成离散时间域下的CCVSI模型。图2展示了电流控制器对采样信号的处理过程。为了实现在不过高要求(低通滤波器性能)条件下也能降低电流纹波，需要将电流的同步采样频率设为SPWM载波信号的两倍(T=1/(2fc))。对式(1)进行微分方程求解和加入零阶保持器后，就可以得到同步采样频率的离散时间函数：

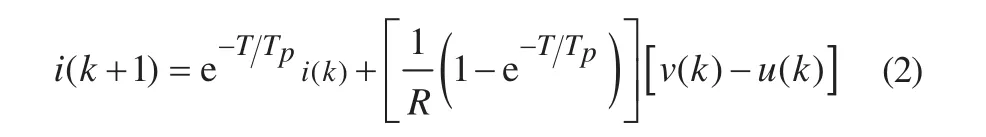
式中：Tp=L/R。

图2为SPWM传输延时原理图。在T(k)时刻，系统将A/D采样得到的电流i(k)送入控制器，控制器计算得到用于生成SPWM的调制比m(k)。但是m(k)不是立即(T(k)时刻)作为输出调制波的给定，而是要到下一拍T(k+1)时刻才会被作为给定进行SPWM驱动信号的调制。显然这种处理过程会使系统的输出电压产生一拍的延时，表达成状态空间变量方式为：

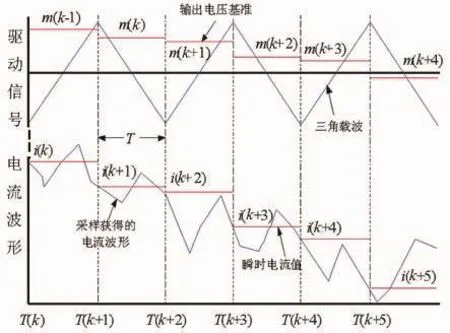
图2 SPWM驱动信号的生成及系统传输延时原理

将(2)、(3)式进行整合，可以得到系统的离散时间状态空间模型：

可得：

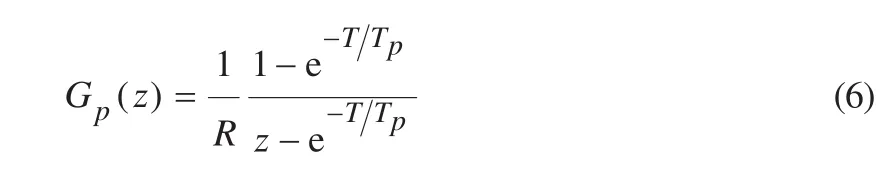
在建立了主电路逆变器—负载之间的状态空间模型和z域下的传递函数后，接下来要设计离散CCVSI型系统的输出电流控制器。目前广泛应用的离散反馈控制CCVSI系统模型如图3所示。系统采用PR控制，图中i*(k)和e(k)分别表示期望得到的理想电流基准和实际测得的电流误差。

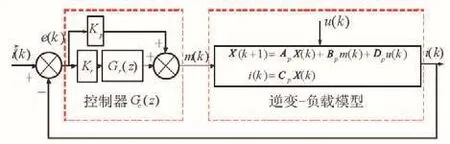
图3 离散反馈控制CCVTSI系统模型

采用PR控制器，其传递函数可表示为：

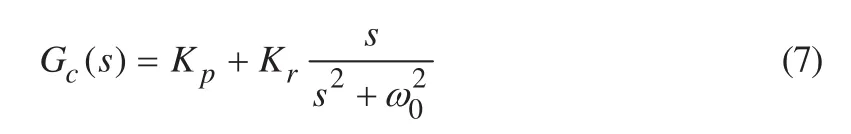
式中：Kp和Kr分别表示PR控制器的比例和谐振系数，ω0=2πf0。将式(7)进行Tustin变换可得：

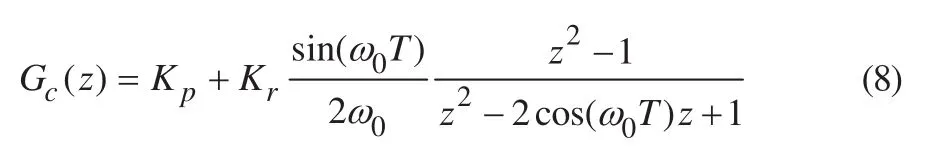
PR控制器中的Kp和Kr可通过常用的频域法得到。本文设计的控制器以获得闭环控制下的最大带宽ωc和相位裕度φm为原则。根据文献[2]的结论，经过PR控制器调节后，系统带宽通常可达到载波频率的10%。若已知预期设计目标φm和采样周期T，可利用经验公式得到合适的带宽ωc，具体表达式为：

当带宽ωc确定后，可分别得到PR控制器的两个参数：

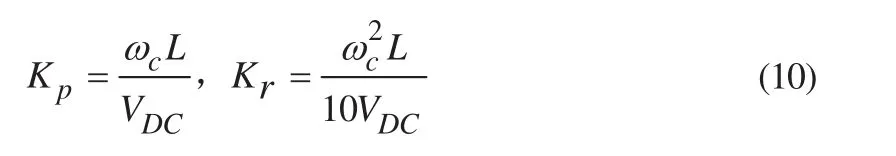
通过对式(4)、(8)的分析可知，整个CCVSI系统共有4个自由变量，但PR控制器只有2个自由度(Kp和Kr)。理论上，只要系统的所有状态变量都能被检测和反馈，就可使整个CCVSI系统具有足够的自由度(系统可被完全控制)，而且在保证系统稳定的前提下还可以任意选择所有闭环极点位置。这样做的好处是可以让系统闭环带宽接近奈奎斯特限制频率。本文要做就是设计一个具有足够自由度的控制器，并在此基础上改进原有设计策略的不足。

本文所期望的控制器结构框图如图4所示。为了实现全状态变量反馈，在控制器中引入了K1至K4四个状态反馈系数。由于开关管输出的相电压呈非线性特性，因而无法对SPWM驱动信号传输过程中产生的延时直接测量，但通过式(3)可对其进行估算：

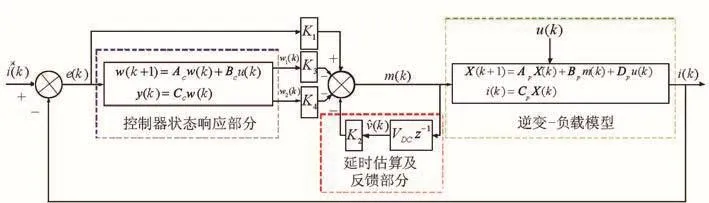
图4 具有延时估算及全状态反馈功能的电流控制型逆变器系统框图

此外，为了能够将系统内部的状态反馈给控制器，需将式(8)的控制器转换成状态空间形式。根据状态反馈型控制器的标准设计形式，式(8)可表示成：

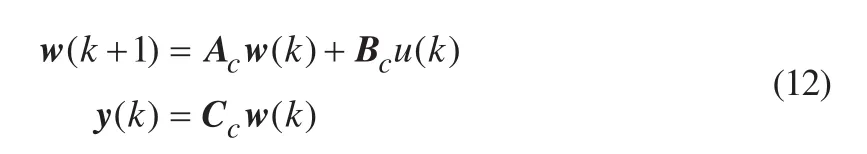
2 基于状态反馈控制的电流控制器设计

2.1 系统能控性和能观性分析

在利用状态反馈控制规律的极点配置法对系统电流控制器进行设计之前，本文将先对整个系统进行能控性和能观性分析[3]。若系统完全可控，就可以根据所建立的状态空间模型来设计离散时间域内的CCVSI系统的控制器模型和逆变—负载模型结合的完整状态空间模型，可得到标准状态空间方程，其具体表达形式为：

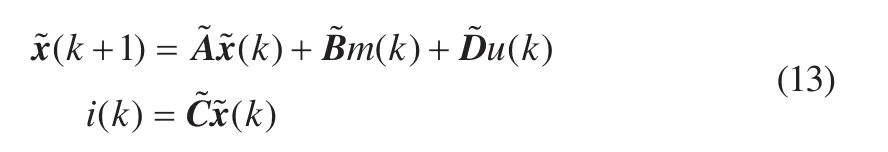
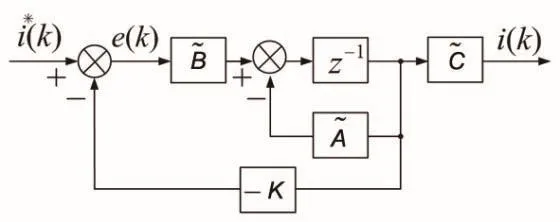
图5 状态反馈控制结构框图

本文所使用的CCVSI型系统参数如表1所示。

表1 仿真实验中所用的CCVSI型系统参数

将表1中的数据分别代入式(13)后，可得到用于判断能控性和能观性的相应矩阵。从计算结果可以得到：50Hz下CCVSI系统能控性矩阵的秩为4，满秩；能观性矩阵的秩为2。因此该条件下的系统是完全能控的。

通过对系统能控性和能观性的分析判断可知，本系统可利用离散系统的状态反馈控制规律的极点配置法求取期望的反馈系数K1至K4[2]。这种方法与其他经典的通过输出量反馈来设计闭环参数的方法相比较有许多优点，它不但可以根据需要将极点配置在任意位置，而且可提高系统的瞬态响应和鲁棒性。

2.2 控制器参数设计和性能分析

在确定完期望的配置极点后，我们求取基于状态反馈控制规律的控制器理想系数K1至K4。在得到状态反馈增益矩阵后，作为比较，本文也设计了经典PR控制器下的参数，其中相位裕度φm=60o。两个控制器参数分别列于表2中。

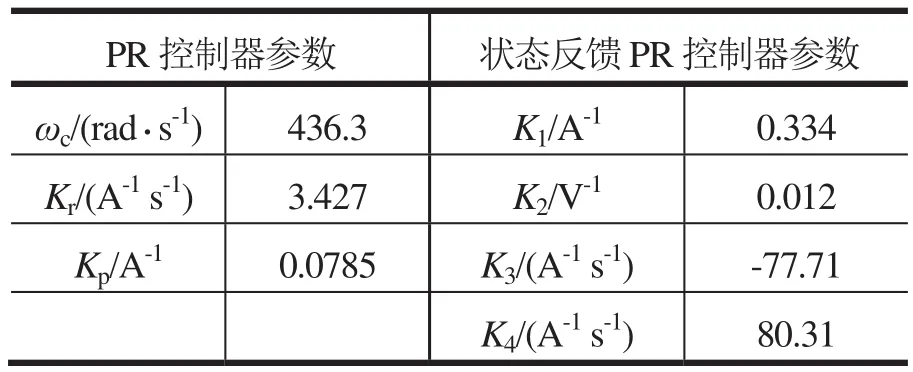
表2 用于实验比较的两个控制器参数

图6为PR控制和状态反馈控制的系统Bode图。通过分析可知，基于全状态反馈的控制可提高低频逆变系统的增益(增加6dB)，而且也能将系统带宽提高至Nyquist极限频率的25%左右，从而改善系统的动态响应。同时，状态反馈控制还可以减少调节时间和系统的稳态误差。

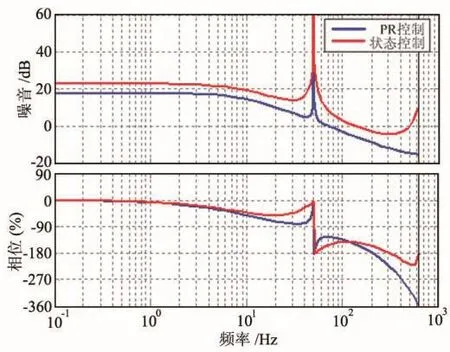
图6 PR控制和状态反馈控制系统开环Bode图

2.3 系统鲁棒性分析

实际使用的控制器与系统都会要求有较强的鲁棒性。但是高增益的调节策略又往往会把鲁棒性变差[4]。通过滤波电感参数的变化，比较了PR控制和状态反馈控制下闭环系统的零极点变化过程(图7)。从图中可以发现，虽然在额定电感值处状态反馈控制时系统的动态性能要优于PR控制，但为了获得较大的带宽其增益过高，导致系统零极点对电感参数的变化敏感，更易移动到单位圆外，使系统不稳定。而状态反馈控制策略可使电感系数在额定值的60%范围内变化时保证系统稳定。与PR控制方式相比，利用状态反馈控制的系统可在所有性能适当提高的条件下保证还有较强的鲁棒性。

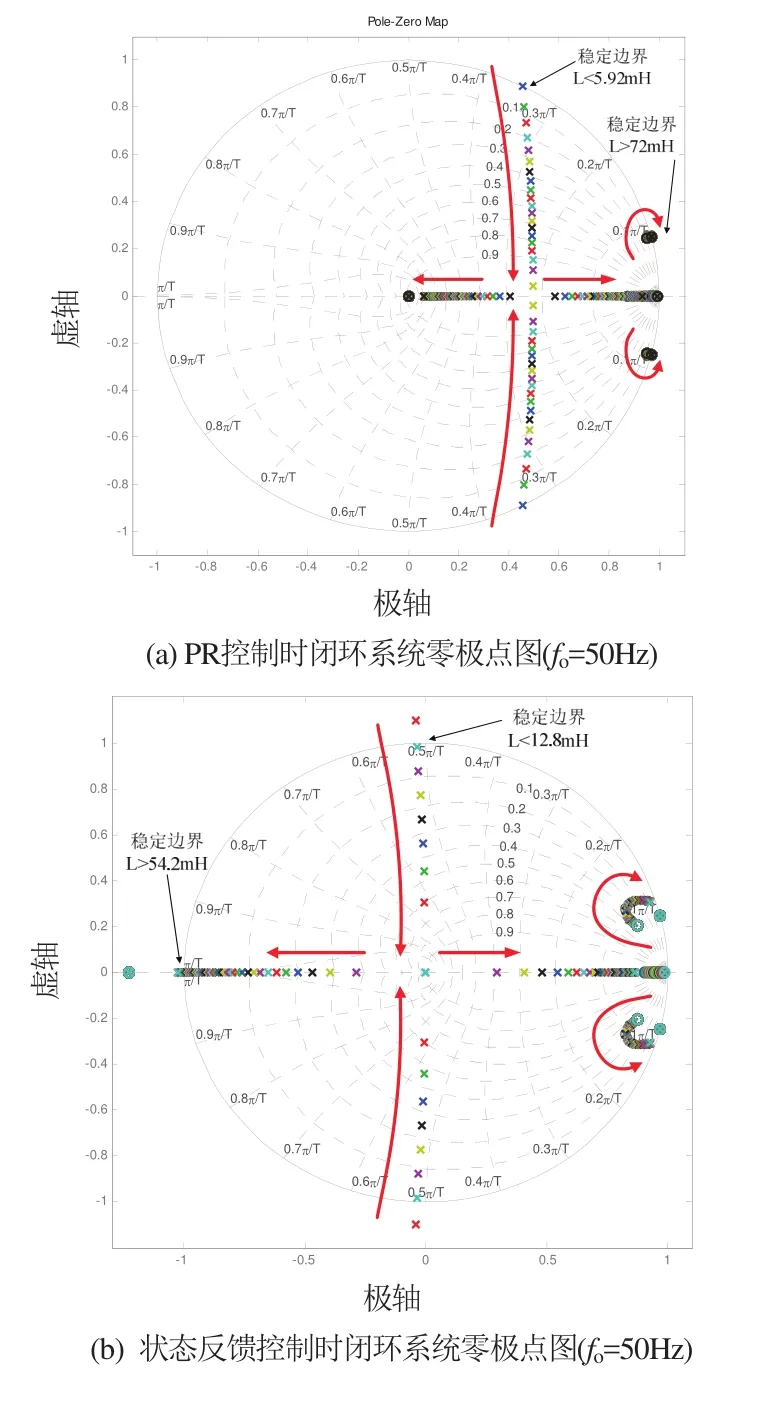
图7 基于PR控制和状态反馈控制的闭环系统零极点图

3 Matlab仿真分析

利用Matlab仿真平台对两种不同的控制策略进行仿真比较，结果如图8所示。

分析图8可以知道，状态反馈控制可以明显提高系统的动态响应，且提高倍数达到3倍以上，而且状态反馈控制还可以提高系统稳态误差。唯一的不足是基于状态反馈控制的系统超调比较大，但50%以下的超调对逆变器是允许的。因此基于状态反馈控制规律的极点配置法所设计的控制器与传统的PR设计方式相比具有更好的动态性能。

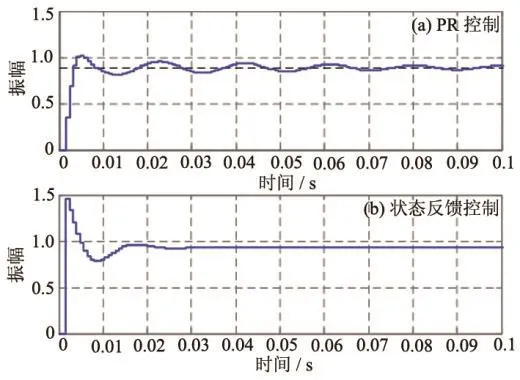
图8 基于PR和状态反馈控制的系统阶跃性能仿真比较图

4 结语

本文基于全状态变量反馈控制规律的极点配置方式，提出了一种改进的电流控制策略，以解决在对大功率和航空电源装置电流控制器进行设计时，传统方法所无法避免的动态响应不理想的难题。通过状态反馈控制规律的极点配置这一方法，提高了系统的稳定性，实现了控制器增益的理想设计。仿真实验表明，在低脉冲比逆变器的控制器设计时，基于状态反馈控制规律的极点配置法所设计的电流控制器与经典的PR设计方式相比，具有更高的效率和更好的动态性能。

[1]Kazmiekowski M P,Malesani L.Current controltechniquesfor three-phase voltage-source PWM converters:A survey IEEE Trans.Ind.Electron,1998,45(5):691-703.

[2]刘 飞.三相并网光伏发电系统的运行控制策略[D].武汉:华中科技大学,2008.

[3]Yepes A G,Freijedo F D,Doval-Gandoy J,et al.Effects ofdiscretization methods onthe performance of resonant controllers IEEE Trans.Power Electron,2010,25(7):1692-1712.

[4]Hodel A S,HallC E.Variable-structure PID control to preventintegrator windup[J].IEEE Trans.Ind.Electron,2001,48(2):442-451.

Design of Inverter Current Controller Based on State Feedback Control

BAI Xianghua,XU Chen
(Navy Representative Office of Aerospace Mechanical and Electrical System in Nanjing District,Nanjing 210006,China)

When AC current controller of low pulse inverter is designed by using the traditional control strategy,the controller system bandwidth usually closes fundamental frequency of the system to lead to the variation of dynamic system response.An improved current control strategy is presented.This problem is overcome by pole placement method of the state feedback control to greatly improve the linear controller gain.Taking the linear state space design under discrete conditions as the principle,the design of current controller can make dynamic response and stable performance of the control system more superior.And the system has stronger robustness.Finally the design results are simulated.The results show that devised current controller based on the pole placement method of the state feedback control law has better dynamic performance compared with that of the traditional PR design scheme.

inverter control; current controller; state feedback; pole placement

TM464

A

柏祥华（1987-），助理工程师，本科，研究方向：舰艇动力。