基于观测器的具外部扰动的离散时间系统的滑模控制

高 超，高存臣

（中国海洋大学数学科学学院，山东 青岛266100）

滑模变结构控制的最大优点是对不确定参数和外部扰动具有不灵敏性，这一良好的性质对控制系统的设计带来诸多好处，因而受到控制工作者的青睐，成为设计系统控制器的主要方法之一。自从Utkin V［1］提出滑模变结构以来，许多学者研究了滑模变结构的性质和设计方法。但是，目前大部分研究成果是在连续时域内得到的。随着计算机技术的飞速发展和工业自动化等领域的实际需要，表述控制系统的模型不但有连续模型，而且还有离散模型，这就需要研究离散控制系统的性质与控制器的设计，因此用滑模变结构控制方法研究DTS的分析与设计问题具有重要的理论价值和实用价值。然而，由于采样周期的影响，在连续时域内得到的滑模控制的某些性质却并不适用于DTS。因此，许多学者开始研究DTS的切换流形与滑模控制器的设计方法［2－6］。

高为炳［7］提出了离散滑模控制的定义，并给出了DTS的趋近律。文献［3］在文献［2］的基础上讨论了利用离散趋近律设计不确定DTS的变结构控制问题，分析了离散趋近律造成系统颤振的原因，给出了改进的离散趋近律，并利用它设计了变结构控制律。文献［8］讨论了线性多变量离散不确定系统滑模变结构控制问题，并利用全程滑动模态的思想，通过构造切换函数，使系统的状态轨线一开始便落在切换面上，缩短了到达时间，增强了系统的鲁棒性。文献［9］分别提出了积分型变结构控制和积分型滑模控制技术。然而，在上述文献中，关于控制器的设计都是在假设系统的状态可观测的条件下完成的，但在实际应用中，这个假设不一定总是成立的，因此一个很自然的问题就是如何利用输入、输出的信息对系统实现状态重构。文献［10］针对未知输入线性连续系统提出了全阶观测器的设计方案。文献［11］针对未知输入线性连续系统提出了降阶观测器的设计方案。文献［12］提出了基于观测器的MIMO连续时间系统的滑模控制器的设计方案。因此，对于状态不可观测的DTS，如何给出切换曲面与滑模控制器的设计方案便是一个需要解决的问题。

本文在文献［10］的基础上，针对上述问题，通过对DTS设计一种改进的状态观测器，研究DTS的稳定性。并将上述结果推广到具有扰动的MIMO不确定DTS。改进后的方案具有设计方便，易于应用和收敛速度快等优点。然后针对外部扰动满足匹配条件的DTS进行了控制器的设计。对外部扰动采用了扰动估计器［13］来估计扰动的值，这样就不需知道扰动的上界，降低了对扰动的要求，增强了实际应用性。扰动估计器对满足缓时变条件［9］的扰动的估计效果是很好的，特别是对常值扰动，可达到理想的预期。

1 观测器的设计

考虑如下MIMO不确定DTS

其中：x∈Rn为系统的状态向量；u∈Rm为控制向量；fRp为外部扰动向量；y∈Rq为系统的输出向量；系数矩阵A∈Rn×n；B∈Rn×m；C∈Rq×n为已知的常值矩阵，且满足rank（B）＝m。

对系统（1），作如下假设：A1）矩阵对（A，B）完全可控；A2）矩阵对（A，C）完全可观。

现在，构造系统（1）的观测器如下：

其中：矩阵L∈Rn×q；E∈Rn×q；H ∈Rn×q待定；xe（k）为观测到的状态变量。定义

则有

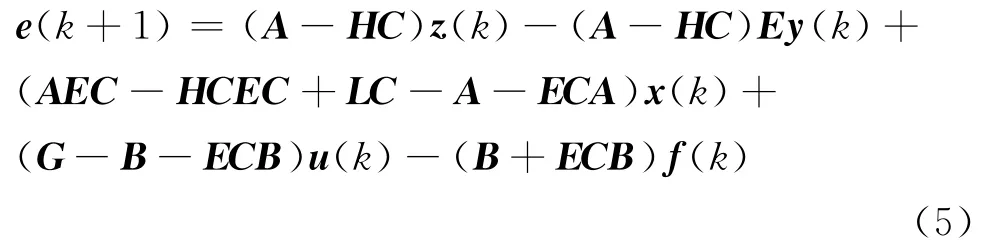
如果令：

则

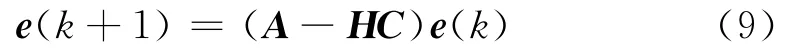
现确定矩阵H，E，L，G使得它们满足（6）～（8）式。

首先由假设A2，（A，C）完全可观，据对偶性原理［14］，（A′，C′）完全可控，于是存在矩阵K ，使得 具有事先给定的极点，此时取

其次再来确定E。考虑如下2种情况

情形1 rank（CB）＝q，且q＝m。此时，CB可逆，

由式（8），可得

由式（7）和（11），有

由式（6）、（10）和（11），有

情形2 rank（CB）＝q，且q＜m。此时，存在非奇异矩阵Q，使得QCB＝J［］0T，其中矩阵J∈Rp×p可逆，于是可得

其中α∈ Rn×（q－p）可任意确定。

当确定出矩阵E后，由式（7）可确定出

最后，经过适当选取E中的任意项α的元素，可确定出矩阵L。

注1 当rank（CB）＜p时，式（8）没有解，此时，观测器是不存在的［10］。

注2 上述第二种情形下，通过式（14）计算E时，先不给任意项α赋值，然后结合式（6）和（10），适当的选取α，确定出矩阵L，最后再经过式（12）确定出G。

2 滑模面设计

考虑系统（1）的变结构控制问题。在变结构控制的设计中，滑模面的设计是1个非常重要的环节，1个好的滑模面可以保证系统有良好的动态品质。以下，基于上述的观测器来设计滑模面。

引理1 在假设A1的条件下，如果存在列满秩矩阵M ∈Rm×n，使得 MB 可逆，则A－B（MB）－1MA 有m个零特征值和n－m个非零特征值。

注3 由引理1，可选择1个列满秩矩阵M∈Rm×n，使得MB 可逆，并且A－B（MB）－1MA 具有稳定的极点［7］。

现在，选择系统（1）的切换函数如下

考虑到状态x（k）不可测，考察观测器的xe（k）的状态方程，由式（2）、（3）、（6）、（7）及（8）可得

或

可解出等效控制：

将式（20）带入（1），可得系统（1）的滑模方程如下：

因此，由状态x（k）和状态误差e（k）所组成的闭环系统可描述为

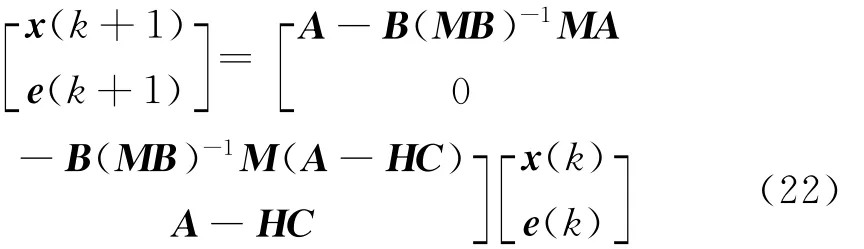
因为M和H 的选择分别使得A－B（MB）－1MA和A－

3 滑模稳态分析及控制器设计

上述等效控制ueq中含有外部扰动项f（k），但实际中f（k）往往是未知的，所以ueq并不能实际应用。在对待未知外部扰动的问题中，以往文献中的控制器是按它的上下界来设计的，也就是说按最坏情况来设计的，这样系统就达不到削弱抖振的目的。本段中，先分析滑动模态的稳定性，然后对缓时变函数f（k），采用文献［13］中的单位周期延迟的方法来估计f（k），并以此来设计控制器。

此时，设计控制器如下

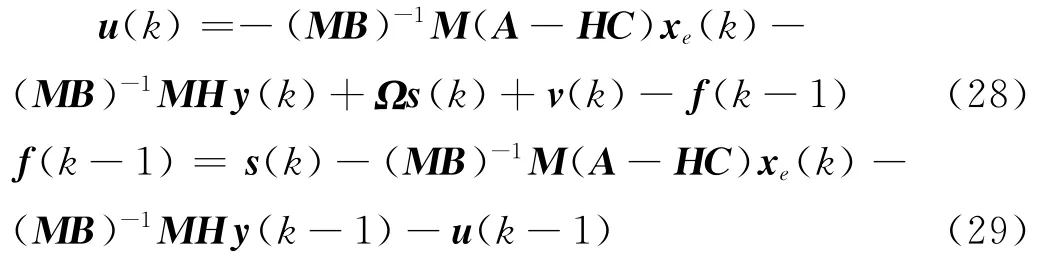
其中Ω＝diag（q1，…，qm）∈Rm×m为对角矩阵，满足条件控制输入v（k）∈Rm稍后设计。式（18）两边同时左乘 （MB）－1M 并将式（28）代入，得到

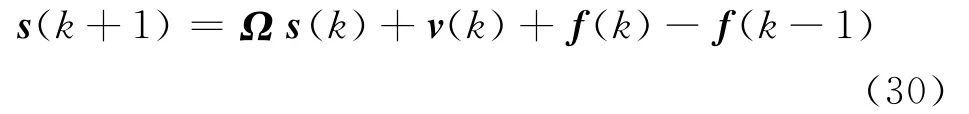
注4 这里只需要知道外部扰动f（k）之差分的上界，而不要求知道f（k）的上界，即η，从而降低了对f（k）的要求。其中η是随着采样频率增加而减小的。特别地，当f（k）为常值扰动时，则有f（k）＝f（k－1），从而就得到了f（k）的精确估计。如果f（k）不是常值扰动，但满足缓时变条件，那么由（29）得出的估计值也能达到精度要求。

4 数值仿真

对系统（1），取

图1 状态误差曲线Fig.1 State error curve

图2 状态变化曲线Fig.2 State change curve

图3 实际扰动及估计扰动曲线（放大后）Fig.3 Actual perturbation and disturbance estimation curve

图4 系统输入曲线Fig.4 System input curve

5 结语

本文改进了文献［10］中对带有扰动的MIMO离散系统设计状态观测器方法，改进之后的方法计算更简单有效。并根据观测器的状态方程设计了原系统的控制器，在设计控制器的过程当中，对满足缓时变条件的外部扰动采用了单位周期延迟的方法来估计扰动项的值，仿真结果表明，本文中设计的方法收敛速度更快，而且有效地克服了系统中的抖动现象。

［1］ Utkin V.Variable structure systems with sliding modes［J］.IEEE Transactions on Automatic Control，1977，22（2）：212－222.

［2］ Gao Weibing，Wang Yufu，Homaifa A.Discrete－time varia ble structure control systems［J］.IEEE Transactions on Industrial E－lectronics，1995，42（2）：117－122.

［3］ 翟长连，吴智铭.不确定离散时间系统的变结构控制设计［J］.自动化学报，2000，26（2）：184－192.

［4］ Bartolini G，Ferrara A，Utkin V.Adaptive sliding mod e control in discrete－time systems［J］.Automatica，1995，31（5）：769－773.

［5］ Eun Yongsoon，Kim Jung－Ho.Discrete－time variable structure controller with a decoupled disturbance compe nsator and its application to a CNC servomechanism［J］.IEEE Transactions on Con－trol Systems Technology，1999，7（4）：414－423.

［6］ Cheng Chih－Chiang，Lin Ming－Hsiung，Hsiao Jia－ming.Sliding mode controllers design for linear diecrete－Time systems with matching perturbations［J］.Automa－tica，2000，36（8）：1205－1211.

［7］ 高为炳.变结构控制的理论及设计方法［M］.北京：科学出版社，1996：278－299.

［8］ 米阳，李文林，井元伟，等.线性多变量离散系统全程滑模变结构控［J］.控制与决策，2003，18（4）：460－467.

［9］ Pai MingChang.Robust tracking and model following of uncertain dynamicsystems via discrete－time integral sliding mode control［J］.International Journal of Control，Automation and Systems，2009，7（3）：381－387.

［10］ Yang F，Wilde Rw.Observers for linear systems with unknown inputs［J］.IEEE Transactions on Automatic Control，1988，33（7）：677－681.

［11］ Hou M，Muller P C.Design of observers for linear systems with unknown inputs［J］.IEEE Transactions on Automatic Control，1992，37（6）：871－875.

［12］ Chang JeangLin.Discrete－time sliding mode controller design with state estimator and disturbance observer［J］.Electrical Engineering，2007，89（5）：397－404.

［13］ Su WuChung，Drakunov S V.An boundary layer in sliding mode for sampled－data system［J］.IEEE Transactions on Automatic Control，2000，45（3）：482－485.

［14］ 赵明旺，王杰，江卫华.现代控制理论［M］.武汉：华中科技大学出版社，2007.