车辆网络中实时的邻居位置获取协议

邓左祥

(上海交通大学电子信息与电气工程学院，上海 200240)

0 引言

根据世界卫生组织调查统计，交通事故平均每年在全世界造成大约120万人员死亡和5000万人员受伤［1］。此外，交通事故还会造成巨大的经济损失［2］。因此，交通事故对人类的危害相当大，采取有效措施来预防交通事故是非常必要的。

无线网络技术的迅速发展，使得利用这些技术来保障交通安全变为可能。作为无线传感器网络在交通中的应用，车辆网络近年来已经成为研究热点之一。车辆网络有许多有意义的应用，比如交通安全［3］和信息共享［4］。

在车辆网络中，如果2辆车在通信距离内，这2辆车就可以互相收发消息，并且称它们互为邻居。随着车载GPS装置［5］的价格越来越便宜，车载GPS装置逐渐开始普及起来。每辆车可以通过车载GPS装置获知自己的位置信息(包含经度和纬度)。一辆车可以将自己的位置信息通过无线的方式传输给自己的邻居。如果一辆车可以实时地获得自己各个邻居的位置，在一定程度上，可以起到保障交通安全的作用。

然而，解决车辆网络实时的邻居位置获取问题是有挑战的。首先，由于每辆车的数据包都包含自己的位置信息，因此，如何实时地获取邻居位置，本质上就是如何减小接收时间间隔(Inter-Reception Time)。接收时间间隔的定义首次在文献［6］提出，但是它并没有提出减小接收时间间隔的方法。其次，为了减少发送数据包的冲突，每辆车都必须竞争信道，如何分配信道成为一个挑战。最后，保证公平性，让各辆车之间的平均接收时间间隔都差不多，这也是非常重要和具有挑战的。

针对车辆网络的邻居位置获取问题，本文提出车辆网络中一种实时的邻居位置获取协议，目标是使车辆网络中的每辆车实时地获知其各个邻居的位置信息。

1 相关工作

车辆网络已经受到越来越多研究者的关注，一些关于车辆网络有价值的研究成果已经形成［7-8］。

文献［9-10］提出2种关于保障交通安全的重复传输协议SFR和SPR。重复传输协议将时间分为一个个时间帧，每个时间帧有L个时槽。在SFR中，每辆车从一个时间帧的L个时槽中，随机选择出w个时槽来传输数据包。在SPR中，每辆车在一个时槽发送数据包的可能性是p，维持空闲即不发送数据包的可能性是1-p。

2 问题提出

2.1 系统模型

当2辆车空间上的欧氏距离小于或等于通信距离时，可以称它们是邻居。2辆互为邻居的车可以互相收发消息。对于任意一辆车，如果它同时收到多辆车的数据包，在这辆车上就会发生数据包冲突。每辆车都安装具有一定通信能力和计算能力的设备。

2.2 问题描述

在车辆a和车辆b作为邻居期间，车辆a可以在不同时刻收到车辆b的数据包。假设在2辆车作为邻居期间，车辆a收到车辆b的k个数据包，用tab(1)，tab(2)，…，tab(k)来表示车辆a收到车辆b数据包的各个时刻。由于车辆b的数据包中包含它最新的行驶数据，因此，每当车辆a收到车辆b的数据包，车辆a都可以知道车辆b的位置。邻居位置获取平均时间间隔的定义如下。

定义1 邻居位置获取平均时间间隔。在车辆a和车辆b的一次作为邻居期间，车辆a对车辆b的位置获取平均时间间隔ηab，可以通过式(1)来计算:

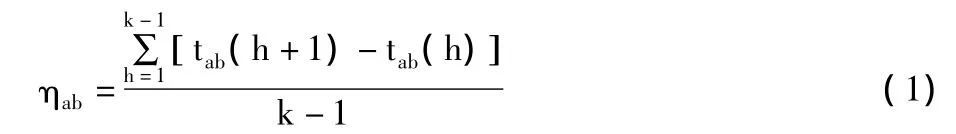
在现实生活中，一辆车可能有很多邻居，车辆a和车辆b也有可能相遇多次，用ηab(k)来表示a和b的第k次作为邻居期间的ηab，用Tab来表示a和b成为邻居的次数。车辆网络中的邻居位置获取问题定义如下。

定义2 邻居位置获取问题。车辆网络中的邻居位置获取问题，就是提出一种协议，目标是最小化所有ηab的平均值，用式(2)表示如下:

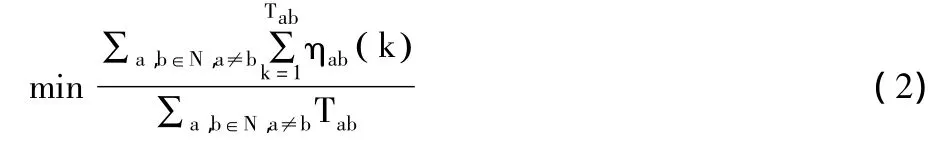
作为有效的邻居位置获取，不仅要使所有ηab的平均值尽可能小，还要尽可能使每个ηab的值都差不多，以保证公平性。此外，还应该尽可能减小计算代价。

3 实时的邻居位置获取协议RNP

3.1 概述

RNP是完全分布的协议。在RNP中，时间被分为一个个时间帧，每个时间帧有θ个时槽。时间帧和时槽在车辆之间是同步的，可以通过车载GPS装置实现同步。为了让邻居获取自己的位置，每辆车的数据包都包含自己最新的车辆行驶数据，以及邻居数量。假设在每个时槽，每辆车都可以通过其车载GPS装置获取最新行驶数据。用τ0来表示一个时槽的时长，τ0在本文中是一个常数。每辆车都存储有关于其邻居的一个列表。在邻居列表里，记录着它每个邻居的行驶数据，以及邻居数量。

RNP分为2个版本，分别是F-RNP和P-RNP，它们都是自适应的协议。在F-RNP中，每辆车在一个时间帧随机选择出ϑ个时槽来发送数据包。在PRNP中，每辆车在一个时间帧的各个时槽以p的概率发送数据包，以1-p的概率不发送数据包。通过理论分析，本小节优化F-RNP的参数ϑ和P-RNP的参数p。此外，还优化每个时间帧的长度θ。

假设车辆网络中任意2辆车a和b，它们互为邻居。假设车辆a有c-1个邻居(其中一个邻居是b)，车辆b有d-1个邻居(其中一个邻居是a)，c≥2，d≥2。对于某个给定的时槽来说，让Pa代表车辆a在这个时槽发送数据包并且车辆b成功收到这个数据包的概率，让Pb代表车辆b在这个时槽发送数据包并且车辆a成功收到这个数据包的概率。让α代表车辆a在这个时槽发送数据包的概率，让β代表车辆b成功收到这个数据包的概率。

3.2 优化 F-RNP

本小节优化F-RNP的参数ϑ。首先讨论2辆车的情况，接着讨论多辆车的情况。

假设车辆a在每个时间帧发送ϑa次，车辆b在每个时间帧发送ϑb次。让，…分别代表车辆a的每一个c-2邻居(除了车辆b)在每个时间帧的发送次数，…，分别代表车辆b的每一个d-2邻居(除了车辆a)在每个时间帧的发送次数。由于车辆a在一个时间帧发送ϑa次，因此可以通过式(3)计算α:

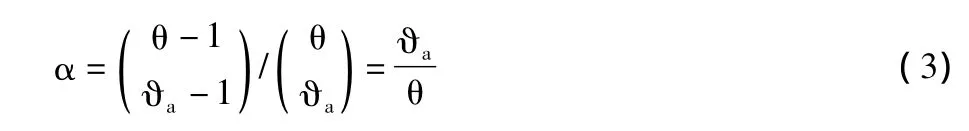
只有车辆b和车辆b的其它d-2个邻居不在这个给定的时槽发送数据包时，车辆b才能成功接收这个数据包。因此，β可以通过式(4)计算:

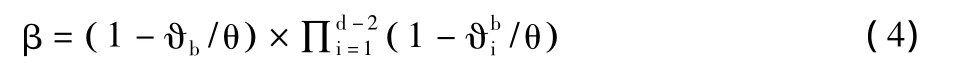
通过α和β相乘，可以得到Pa:

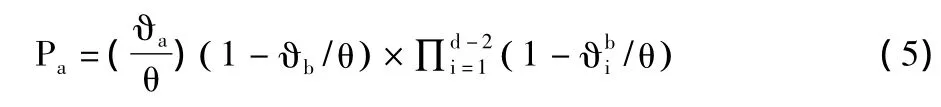
同样，Pb通过式(6)计算得到:)

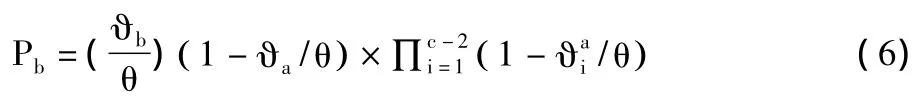
基于公平性，假设车辆a的所有邻居在一个时间帧的发送次数都相等，以及车辆b的所有邻居在一个时间帧的发送次数都相等，这样可以简化式(5)和式(6):

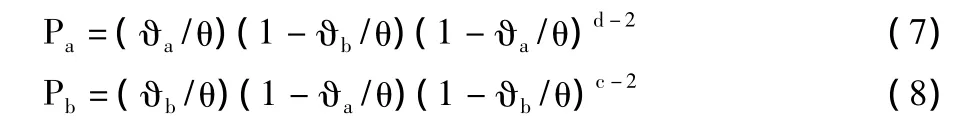
用X表示一个随机变量，含义是经过X个时槽，车辆b才收到车辆a的一个数据包。根据几何分布的定义，X服从概率为Pa的几何分布，其概率分布函数为:

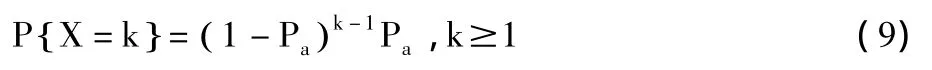
同样，用Y表示一个随机变量，其含义是经过Y个时槽，车辆a才收到车辆b的一个数据包，则Y服从概率为Pb的几何分布，其概率分布函数为:

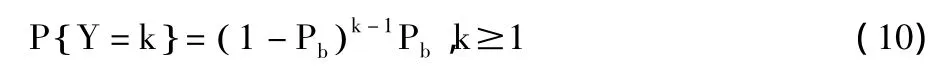
根据几何分布的数学期望，可得X的数学期望为1/Pa，以及Y的数学期望为1/Pb。因此，a和b之间互相收到对方数据包的平均时间间隔为［τ0×(1/Pa+1/Pb)］/2。由于τ0在本文中是常数，因此，为了达到优化目标，让 τ(ϑa，ϑb)=1/Pa+1/Pb，需要最小化 τ(ϑa，ϑb)。

通过求一阶偏导数来最小化函数，可以得到，在c=d的情况下，当ϑa=θ/d和ϑb=θ/c时，可以使τ(ϑa，ϑb)最小化。在 c≠d 的情况下，要使 τ(ϑa，ϑb)最小化，ϑa和ϑb都是包含c和d的代数表达式。此时，计算出ϑa和ϑb的代价非常大。为了减小计算代价，采取近似最优的方法来最小化τ(ϑa，ϑb)。由于在现实生活中，2辆互为邻居的车辆的邻居数量很接近，因而可得c≈d。因此，在c≠d的情况下，可以通过让 ϑa=θ/d和 ϑb=θ/c来近似最小化 τ(ϑa，ϑb)。综上所述，在考虑2辆车的情况下，为了让a和b尽可能实时地获知对方位置，在一个时间帧，车辆a应该发送θ/d次，车辆b应该发送θ/c次。

根据以上结论，在考虑多辆车的情况时，基于公平性，每辆车都根据自己邻居的邻居数量的平均数，来决定自己在一个时间帧的发送次数。例如，假设车辆a的c-1个邻居分别有，…，个邻居，车辆a在一个时间帧的发送次数应该为θ/¯n次，其中¯n通过式(11)计算:

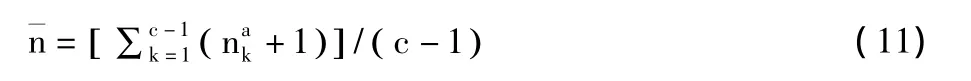
由于道路上车辆的移动，每辆车邻居的邻居数量也会发生变化。因此，根据邻居的邻居数量变化，每辆车在一个时间帧的发送次数也自适应地相应变化。在某个时间帧中，如果一辆车收到它若干个邻居的数据包，根据这些数据包，它可以知道这些邻居的邻居数量。基于这些信息，这辆车按照式(11)计算得到¯n。在下一个时间帧，这辆车的发送次数为θ/¯n次。

3.3 优化P-RNP

本小节优化P-RNP的参数p。首先讨论2辆车的情况，接着讨论多辆车的情况。

假设车辆a在一个时间帧的每个时槽发送数据包的概率是pra，不发送数据包的概率是1-;车辆b在一个时间帧的每个时槽发送数据包的概率是prb，不发送数据包的概率是 1-prb。让，…，分别代表车辆a的每一个c-2邻居(除了车辆b)在一个时间帧每个时槽的发送概率，，…，分别代表车辆b的每一个d-2邻居(除了车辆a)在一个时间帧每个时槽的发送概率。容易看出，α=pra。另外，β可以通过式(12)计算:

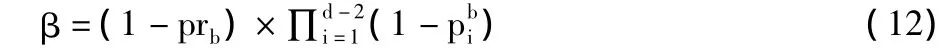
通过α和β相乘，可以得到Pa:

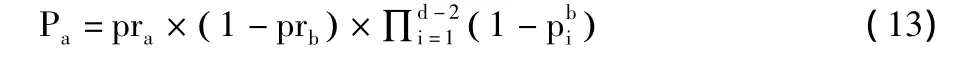
同样，Pb通过式(14)计算得到:

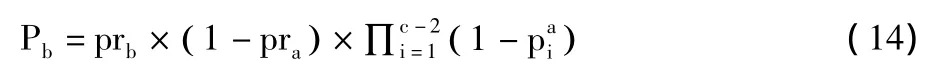
基于公平性，假设车辆a的所有邻居在每个时槽的发送概率都相等，以及车辆b的所有邻居在每个时槽的发送概率都相等，这样可以简化式(13)和式(14):

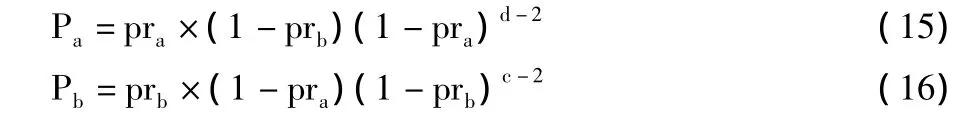
和上一小节一样，车辆a和车辆b之间互相收到对方数据包的平均时间间隔为［τ0×(1/Pa+1/Pb)］/2。为了达到优化目标，让 τ(pra，prb)=1/Pa+1/Pb，需要最小化 τ(pra，prb)。

通过求一阶偏导数来最小化函数，可以得到，在c=d的情况下，当pra=1/d和prb=1/c时，可以使τ(pra，prb)最小化。在c≠d的情况下，计算出pra和prb的代价非常大。为了减小计算代价，通过让pra=1/d和prb=1/c来近似最小化τ(pra，prb)。综上所述，在考虑2辆车的情况下，为了让a和b尽可能实时地获知对方位置，在一个时间帧每个时槽发送数据包的概率，车辆a应该为1/d，车辆b应该为1/c。

根据以上结论，在考虑多辆车的情况时，基于公平性，每辆车都根据自己邻居的邻居数量的平均数，来决定自己在一个时间帧每个时槽发送数据包的概率。根据邻居的邻居数量变化，每辆车在一个时间帧每个时槽发送数据包的概率也自适应地相应变化。在某个时间帧中，如果一辆车收到它若干个邻居的数据包，基于这些信息，这辆车按照式(11)计算得到¯n。在下一个时间帧，这辆车在每个时槽发送数据包的概率为1/¯n。

3.4 获知邻居数量

由于每辆车数据包里包括它的当前邻居数量。因此，一辆车需要一种方法来获知它的邻居数量。每辆车都保存其邻居的一个列表。在邻居列表中，记录它各个邻居的行驶数据。如果一辆车收到另一辆车的数据包，这辆车就通过其邻居列表的车辆ID，来判断另一辆车是否属于新邻居。如果是新邻居，这辆车就对它的邻居数量加1。另外，采取预测的方法来判断一个邻居是否还是邻居。由于数据包包含行驶数据，根据行驶数据，基于车辆保持匀速直线运动的假设，预测2辆车不再是邻居的时刻。例如，假设在时刻t0，车辆a和车辆b分别位于A点和B点，a收到b的数据包。让τab(t0)表示a和b之间的剩余邻居状态持续时间。假设经过τab(t0)的时间后，a和b分别位于A'点和B'点。车辆a通过方程组(17)，来预测τab(t0):

在方程组(17)中，r代表通信距离，va和vb分别代表车辆a和车辆b的速度。通过求解(17)，可以得到τab(t0)的值。每次车辆a收到车辆b的数据包，车辆a都重新计算得到τab(t0)的新值，重新预测2辆车的剩余邻居状态持续时间。如果经过τab(t0)后，车辆a没有再次收到车辆b的数据包，则在t0+τab(t0)时刻，车辆a就认定车辆b不再是其邻居，对其邻居数量减1。

3.5 优化时间帧的长度

本小节优化时间帧长度θ。既然τ0是一个常数，因此，时间帧的时长由θ来决定。一方面，如果θ太大，就容易造成一辆车的邻居数量变化，而造成优化的参数值不再适用，因此θ不能太大。另一方面，每辆车需要通过在一个时间帧收到的邻居数据包，获知它邻居的邻居数量。这暗示着在一个时间帧，每辆车都应该尽可能收到来自它各个邻居的至少一个数据包，因而θ不能太小。因此，θ的取值很关键。

在F-RNP中，根据 ϑa=θ/d和 ϑb=θ/c，可以得到θ=ϑa×d和 θ=ϑb×c，结合式(7)，可以推出 Pa=［(d-1)d-2/dd-1］× ［(c-1)/c］。在 P-RNP 中，根据pra=1/d和prb=1/c，结合式(15)，可以推出Pa=［(d-1)d-2/dd-1］× ［(c-1)/c］。因此，无论是F-RNP还是P-RNP，都可得Pa=［(d-1)d-2/dd-1］×［(c-1)/c］。由于 c≈d，假设(c-1)/c=(d-1)/d，因此可以得到:

设置阈值λ，让车辆b在一个时间帧收到车辆a至少一个数据包的概率大于λ，可以得到:

由式(19)可以得到:

因为θ不能太大，所以让θ=「log(1-Pa)(1-λ)⏋，当考虑λ为常数时，这是关于d的增函数。因此，θ应该等于「log(1-Pa)(1-λ)⏋，其中 Pa=(n*-1)n*-1/n*n*，n*表示一辆车的邻居数量的平均数。

现实生活中，在不同时间段和不同地点，车流密度可能不同，因此n*值也会不同。一辆车应该根据其行驶路段上相应时刻的n*值，对θ值作相应调整。根据对车辆行驶数据的观察，在同一路段的每天相同时刻，车流密度有很大的相似性。把一天的时间分为一个个时间段(例如，每个小时为一个时间段)。请注意，当划分时间段时，需要保证在每个时间段一条路段的车流密度不会显著变化。根据交通部门提供的交通历史信息，可以得到每条路段上一天各个时间段的n*值。当一辆车进入一条路段后，它应该根据其行驶路段上当前时段的n*值，来调整它的θ值。

下面讨论如何设置λ。根据数据包的大小，τ0通常不超过1毫秒，并且当通信距离为100米时，在城市市区的n*通常不超过50。从这些可以知道，当λ为0.999时，一个时间帧的时长通常不超过1秒。另外，在城市市区内，一辆车的平均速度通常不超过10米/秒，因此，在如此短的1秒内，一辆车的邻居数量不会发生显著变化。综合这些因素，在城市市区内，λ可以介于0.95到0.999之间。在高速公路，相比较城市市区，n*变小，使得一个时间帧的时长变小。因此，虽然高速公路的车速比较快，但是λ也可以介于0.95到0.999之间。在 RNP中，设置 λ 为0.99，因而可得 θ=「log(1-Pa)0.01⏋。

4 仿真实验

4.1 实验方法和参数设置

在仿真实验中，将F-RNP和P-RNP，与前人提出的SFR和SPR［9-10］分别进行性能比较，SFR的参数分别设为8、12 和 16，SPR 的参数分别设为 0.01、0.03和0.05。评价性能好坏的指标是所有邻居之间的位置获取平均时间间隔的平均值。

基于收集到的上海市出租车和公交车的真实车辆行驶数据［11-12］来做仿真实验，这些数据是大约4000辆出租车和2000辆公交车的真实行驶数据，由车载GPS装置实时产生。在仿真实验中，选择上海市区内一条长度约为1600米的双向四车道，总共有400辆车。这些车辆按照真实行驶数据在道路上行驶。当通信距离为100米时，n*大约为45，因此θ应该为555。

每个数据包的大小约为400位，数据传输平均速率是5Mbps。每个时槽的时长τ0设为100微秒。无线信道衰减模型服从幂律路径损耗模型［13-14］。

4.2 实验结果

首先，将F-RNP与SFR进行比较，将P-RNP与SPR进行比较。通信距离从80米变化到120米。

在不同的通信距离下，图1显示F-RNP和3个版本的SFR之间的比较结果。从图1可以看出，在不同的通信距离下，相比较3个版本的SFR，F-RNP中所有邻居之间的位置获取平均时间间隔的平均值都较小。当通信距离是100米时，F-RNP的所有邻居之间平均时间间隔的平均值仅仅约为13毫秒。

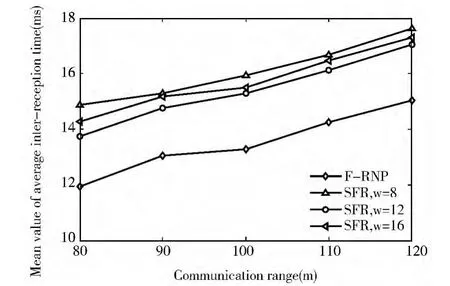
图1 F-RNP与SFR之间的性能比较

在不同的通信距离下，图2显示P-RNP和3个版本的SPR之间的比较结果。从图2可以看出，在不同的通信距离下，相比较3个版本的SPR，P-RNP中所有邻居之间的位置获取平均时间间隔的平均值都较小。当通信距离是100米时，P-RNP的所有邻居之间平均时间间隔的平均值仅仅约为15毫秒。

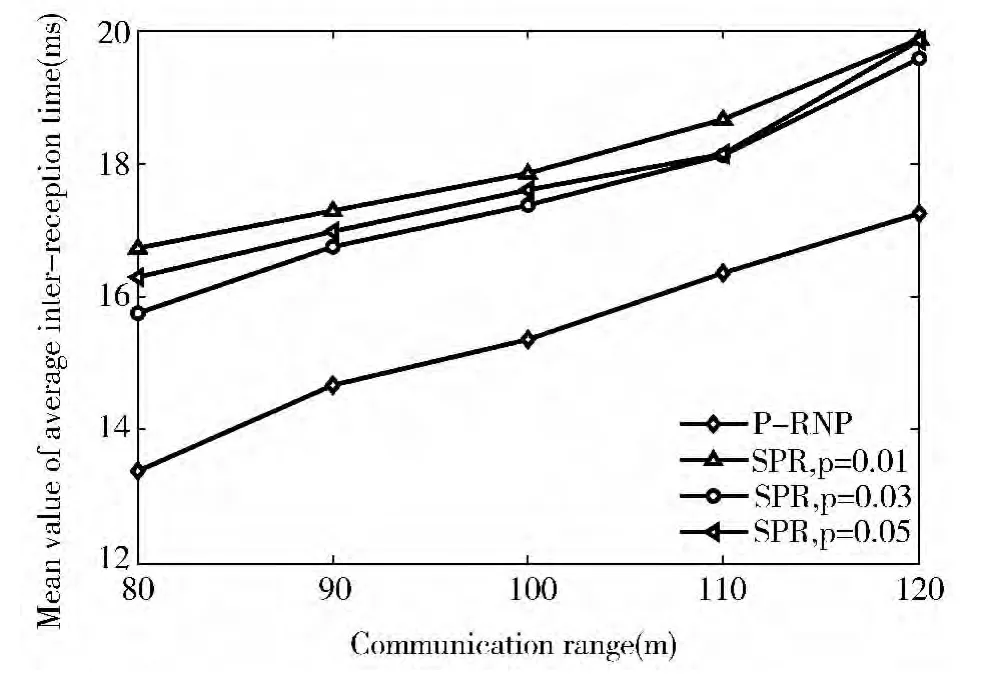
图2 P-RNP与SPR之间的性能比较

为了检验F-RNP的公平性，当通信距离是100米时，从所有邻居之间的位置获取平均时间间隔中，随机选择出100个平均时间间隔。图3显示这100个平均时间间隔之间的差异。从图3可以看出，任意2个平均时间间隔之间的差异都小于4毫秒，这暗示F-RNP实现较好的公平性。

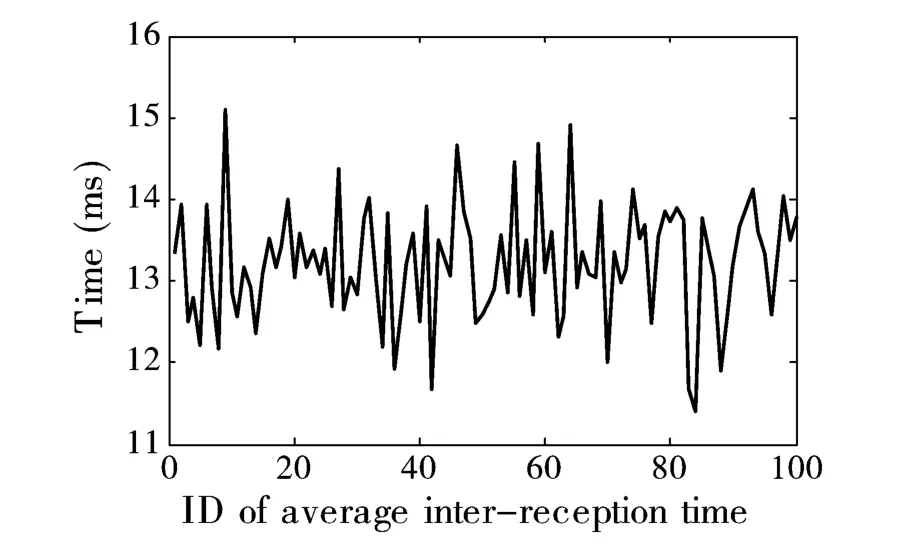
图3 F-RNP中平均时间间隔之间的差异

为了检验P-RNP的公平性，当通信距离是100米时，从所有邻居之间的位置获取平均时间间隔中，随机选择出100个平均时间间隔。图4显示这100个平均时间间隔之间的差异。从图4可以看出，任意2个平均时间间隔之间的差异都小于5毫秒，这暗示P-RNP实现较好的公平性。

图4 P-RNP中平均时间间隔之间的差异

5 结束语

本文关注车辆网络中获取邻居位置的问题，提出一种实时的邻居位置获取协议RNP。RNP分为2个版本，分别是F-RNP和P-RNP，它们都可以让一辆车实时地获知自己邻居的位置。基于真实车辆行驶数据的仿真实验，证实RNP实现较小的位置获取时间间隔，同时还保证公平性。

［1］WHO.The World Health Report 2002-Reducing Risks，Promoting Healthy Life［EB/OL］.http://www.who.int/whr/2002/en/，2013-12-06.

［2］Blincoe L，Seay A，Zaloshnja E，et al.The Economic Impact of Motor Vehicle Crashes，2000［R］.NHTSA Technical Report，DOT HS 809446，2002.

［3］Farnoud F，Valaee S.Reliable broadcast of safety messages in vehicular ad hoc networks［C］//IEEE INFOCOM.2009:226-234.

［4］Zhang Yang，Zhao Jing，Cao Guohong.Roadcast:A popularity aware content sharing scheme in VANETs［C］//IEEE ICDCS.2009:223-230.

［5］Hofmann B，Lichtenegger H，Collins J.GPS Theory and Practice［M］.New York:Springer，2001.

［6］Elbatt T，Goel S，Holland G，et al.Cooperative collision warning using dedicated short range wireless communications［C］//ACM VANET.2006:1-9.

［7］Jeong J，Guo Shuo，Gu Yu，et al.TBD:Trajectory-based data forwarding for light-traffic vehicular networks［C］//IEEE ICDCS.2009:231-238.

［8］Jeong J，Guo Shuo，Gu Yu，et al.TSF:Trajectory-based statistical forwarding for infrastructure-to-vehicle data delivery in vehicular networks［C］//IEEE ICDCS.2010:557-566.

［9］Xu Q，Mark T，Ko J，et al.Layer-2 protocol design for vehicle safety communications in dedicated short range communications spectrum［C］//Proceedings of the 7th International IEEE Conference on Intelligent Transportation Systems.2004:1092-1097.

［10］Xu Q，Mark T，Sengupta R.Medium access control protocol design for vehicle-vehicle safety messages［J］.IEEE Transactions on Vehicular Technology，2007，56(2):499-518.

［11］Huang Hongyu，Luo Peien，Li Minglu，et al.Performance evaluation of SUVnet with real-time traffic data［J］.IEEE Transactions on Vehicular Technology，2007，56(6):3381-3396.

［12］Zhu Hongzi，Li Minglu，Zhu Yanmin，et al.HERO:Online real-time vehicle tracking［J］.IEEE Transactions on Parallel and Distributed Systems，2009，20(5):740-752.

［13］Kunisch J，Pamp J.Wideband car-to-car radio channel measurements and model at 5.9GHz［C］//IEEE VTC.2008:1-5.

［14］Karedal J，Czink N，Paier A，et al.Path loss modeling for vehicle-to-vehicle communications［J］.IEEE Transactions on Vehicular Technology，2011，60(1):323-328.