独塔斜拉桥静风稳定性分析

朱爱东

(大连理工大学土木工程学院，辽宁 大连 116024)

斜拉桥以跨越能力大、桥型优美以及良好的经济性等优点得到了迅速发展［1］。随着桥梁跨度越来越大，越来越柔，结构的静风稳定性问题日益凸显出来。以前大多数专家学者把主要精力放在研究桥梁结构的动力失稳问题上，这是因为根据以往经验，大跨径桥梁结构的静风失稳风速要比结构的颤振临界风速高。目前，桥梁结构的空气动力问题已得到妥善的解决，但对空气静力问题的研究仍然欠缺［2－3］。静风稳定性分析方法主要有侧倾失稳线性方法、扭转发散线性方法、三角级数非线性方法和增量迭代非线性方法［4］。

某独塔钢箱梁斜拉桥所在地区台风灾害比较频繁，周围环境开阔，地表类别为A类。桥梁跨度布置为(40+160+200+40)m，主梁高2 m、宽13.8 m，如图1所示。本文对该桥进行抗风性能分析，采用计算流体动力学(CFD)数值模拟，用连续攻角的方法求出主梁三分力系数(阻力系数、升力系数和扭矩系数)。用有限元软件Midas/Civil建立模型，通过考虑风攻角、风荷载等因素对独塔斜拉桥进行了静风稳定性分析。

图1 主梁标准横断面图

1 静风荷载、静力三分力系数

气流绕过主梁断面，改变了流场的特性，从而产生了风荷载。桥梁断面的静力风荷载由阻力FD、升力FL与扭矩MT组成。传统上，静力三分力系数是通过风洞试验测量获得。近年来，随着CFD技术的应用发展，也可以通过CFD软件数值模拟得到。斜拉桥主梁单位长度静力风荷载可以表示［5］为

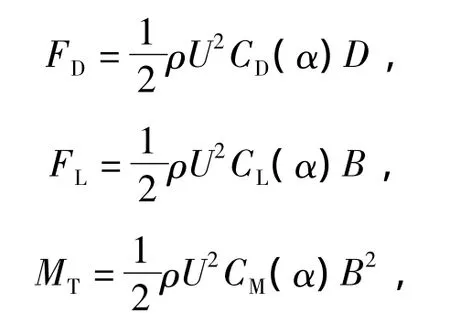
式中 U 为来流平均风速，m/s;CD(α)、CL(α)、CM(α)分别为主梁体轴坐标系下的阻力系数、升力系数与扭矩系数，均为风攻角α的函数;D、B分别为主梁断面的高度和宽度，m;ρ为空气密度，kg/m3。

随着计算速度的迅速发展和计算流体力学技术的改善，基于CFD技术的数值模拟成为识别桥梁结构气动参数的一种新的有效手段［6－7］。采用CFD数值模拟，用连续攻角的方法求出主梁断面的三分力系数，三分力系数在不同风攻角下的变化曲线如图2所示。

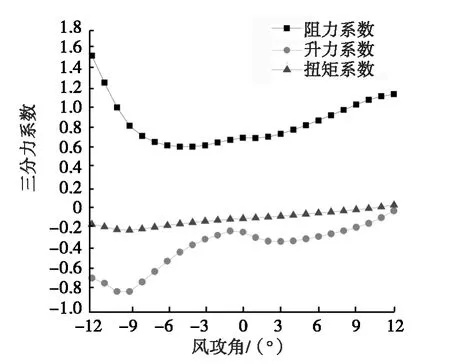
图2 主梁断面静力三分力系数随风攻角的变化曲线

2 结构自振特性分析

桥梁结构动力特性能准确反映出结构的质量和刚度信息。要研究桥梁风致振动问题，首先要分析桥梁结构的动力特性［8－9］。采用Midas/Civil软件建立斜拉桥的有限元分析模型，模拟实桥结构的质量、刚度和边界条件。采用Lanczos算法计算分析结构的动力特性，得到主梁的一阶竖弯振动频率为0.523 Hz，一阶扭转振动频率为1.971 Hz，为进一步研究桥梁风致振动提供依据。成桥状态的主要振型图如图3所示。

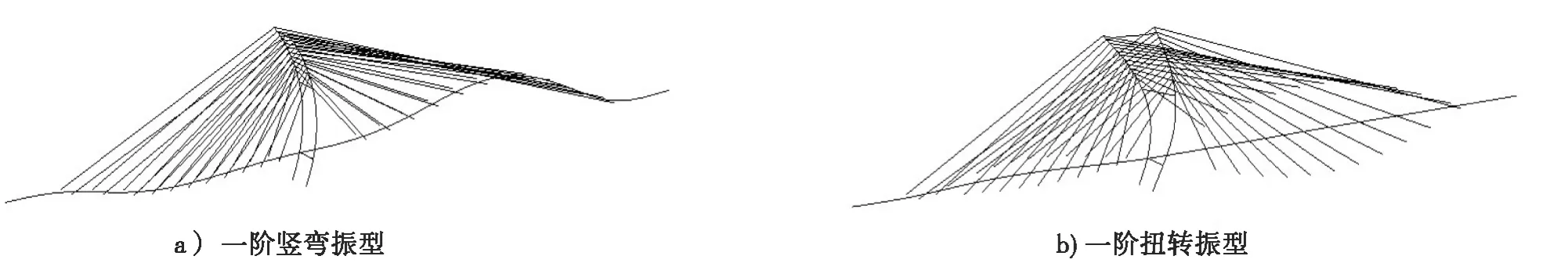
图3 成桥状态振型图

3 静风失稳原理及静风扭转发散临界风速

静风失稳突发性强，一般没有明显预兆，失稳的破坏性非常大［10－12］。当初始风荷载作用于桥梁结构，结构产生位移变形，由于静力三分力系数是结构变形(扭转角)的函数，导致静力三分力系数变化，从而引起外荷载增量，外荷载增量又会引起结构的位移增量，发散机理可以用数学公式表示为

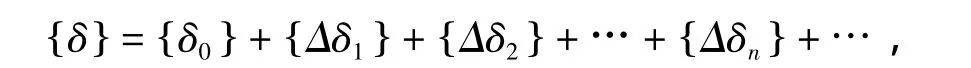
于是，把结构是否会出现扭转发散转换为以上无穷级数的收敛问题，通常认为级数项小于给定收敛向量时，级数收敛。

按照文献［13－14］的说明，斜拉桥静力扭转发散临界风速Ucr为

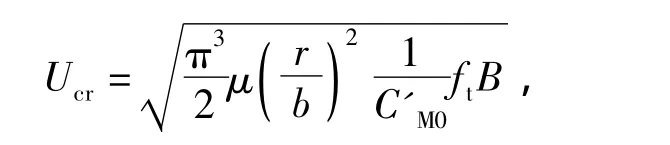
式中 C'M0为0°攻角时主梁断面升力矩系数的斜率;ft为扭转基频，Hz;b为主梁半幅宽度，b=B/2，m;r为主梁截面惯性半径，m;μ=ρL/πρb2，其中ρL为桥面系及拉索的线密度，kg/m。

4 静风荷载响应计算分析

使用软件Midas/Civil根据桥梁结构实际信息建立模型，将主梁的三分力按梁单元荷载添加到主梁上。考虑风速为20～100 m/s依次递增10 m/s的条件下，主梁的横向位移、竖向位移和扭转变形的变化情况。分别给出桥梁在初始攻角0°和±3°3种不同工况下主梁随风速变化的静风位移响应。主梁在风荷载作用下的响应见图4～6［15］。其中，横向位移向下游方向为正，竖向位移向上为正，转角绕x正轴为正。

图4 －3°攻角下主跨跨中和边跨跨中的位移

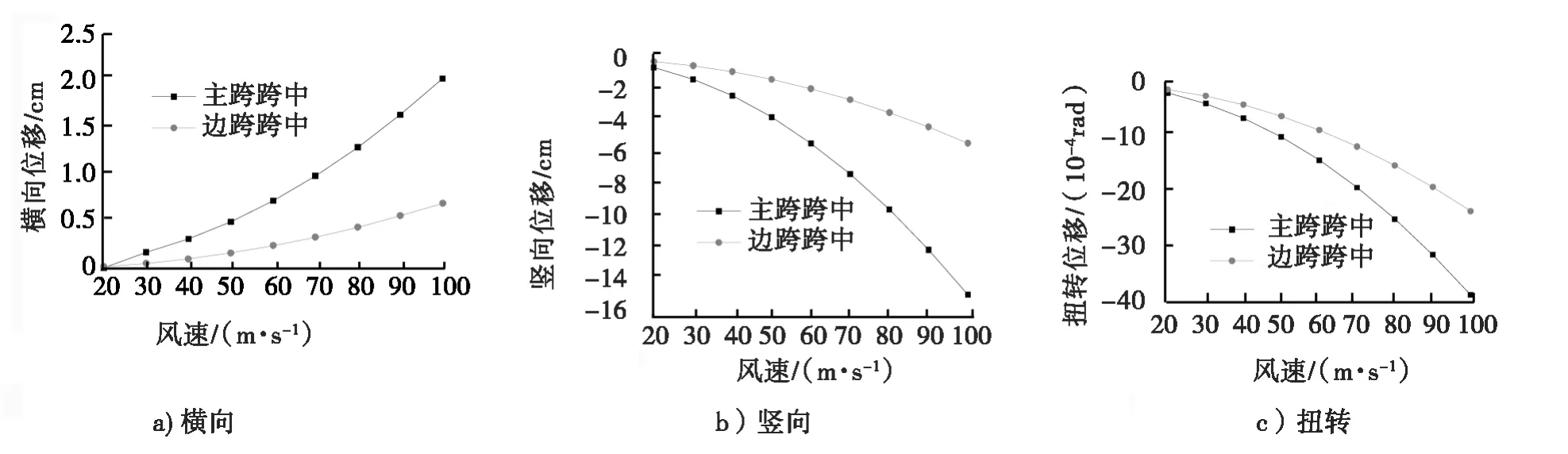
图5 0°攻角下主跨跨中和边跨跨中的位移

图6 3°攻角下主跨跨中和边跨跨中的位移

根据图4～6可知，当风速达到100 m/s时，3种初始攻角条件下均未发生静风失稳，因此结构静风安全性可以得到保障。由于斜拉索和辅助墩的作用，主梁的侧向刚度较大，主梁在静风作用下的横向位移很小。

结构的横向、竖向和扭转位移均显示出非线性的变化。横向位移在+3°攻角时最大，－3°攻角时最小，0°攻角时介于两者之间;竖向位移在3°攻角时最大，0°攻角时最小;扭转位移在－3°攻角时最大，3°攻角时最小。

5 结论

1)该桥的静风稳定检验风速为71.54 m/s。在0°攻角时该风速下主梁主跨跨中的横向位移为1 cm，竖向位移为－7.5 cm，扭转位移为－0.002 rad。

2)一阶对称竖弯的频率为0.523 Hz，一阶对称扭转的频率为1.971 Hz，扭弯频率比为3.769，为研究桥梁风致振动提供依据。

3)主梁结构的横向位移、竖向位移和扭转位移均呈非线性变化。在20～70 m/s的范围内主梁的位移增加缓慢。当风速达到70 m/s后位移增加变快。在检验风速下没有出现位移陡增，该桥具有良好的静风稳定性。

［1］孔祥福，符力国，张珂.近代以来中外桥梁发展概述［J］.山东交通学院学报，2003，11(2):55－58.

［2］唐清华，曹言坤.大跨径桥梁的静风稳定性计算［J］.桥梁建设，2007(增刊2):111－113.

［3］康小方，方诗圣，张利，等.静风荷载下的大跨度斜拉桥稳定性分析［J］.合肥工业大学学报，2012，35(5):652－656.

［4］许福友，陈艾荣.苏通大桥静风响应分析［J］.工程力学，2009，26(1):113 －119.

［5］应旭永.桥梁结构气动参数识别的数值模拟研究［D］.大连:大连理工大学，2012.

［6］张倩.桥梁主梁断面颤振导数的数值模拟研究［D］.成都:西南交通大学，2005.

［7］LARSEN A，WALTHER J H.Aeroelastic Analysis of Bridge Girder Sections Based on Discrete Vortex Simulations［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67＆68:253 －265.

［8］朱乐东，项海帆.桥梁颤振节段模型质量系统模拟［J］.结构工程师，1995，11(4):39－45.

［9］杨军，邱文亮.独塔自锚式悬索桥动力特性分析［J］.山东交通学院学报，2009，17(1):40－43.

［10］谭明伦，段爱忠.钢箱梁独塔斜拉桥抗风性能研究［J］.公路交通科技，2013(7):250－253.

［11］张若刚，韩艳，王金权，等.高桩承台连续刚构桥最大悬臂施工阶段风荷载分析［J］.山东交通学院学报，2009，17(3):53－57.

［12］罗建辉，陈政清，刘光栋.大跨度缆索承重桥梁非线性静风扭转失稳机理的研究［J］.工程力学，2007，24(增刊2):145－154.

［13］中交公路规划设计院.JTG/T D60－01—2004 公路桥梁抗风设计规范［S］.北京:人民交通出版社，2004.

［14］陈政清.桥梁风工程［M］.北京:人民交通出版社，2005.

［15］项海帆.现代桥梁抗风理论与实践［M］.北京:人民交通出版社，2005.