山区夏季地表温度的影响因素——以泰山为例

孙常峰，孔繁花，*，尹海伟，闫伟姣，许 峰，任怡静

(1.南京大学国际地球系统科学研究所， 南京 210023； 2.南京大学建筑与城市规划学院， 南京 210093)

山区夏季地表温度的影响因素
——以泰山为例

孙常峰1，孔繁花1，*，尹海伟2，闫伟姣1，许 峰1，任怡静2

(1.南京大学国际地球系统科学研究所， 南京 210023； 2.南京大学建筑与城市规划学院， 南京 210093)

以泰山为例，应用夏季的Landsat 5的TM6为基本数据源，基于单窗算法定量反演了泰山地表面温度(LST)，在此基础上首先探讨了LST与地形因子的关系，然后比较了归一化水汽指数(NDMI)和归一化植被指数(NDVI)在表达山区LST上的效力，最后利用逐步回归分析法，构建出LST与地形因子、NDMI的回归方程，应用偏相关系数，得出各个因子对LST的影响程度。结果表明：1)在地形因子中，影响LST的主要因素是海拔，随海拔升高呈自然对数形式降低，相比而言，坡度、坡向以及太阳入射能量的影响则很小；2)在没有水体时，NDVI与NDMI都能有效地表达山区的LST，LST与NDVI间是二次项负相关关系，与NDMI间是线性负相关关系，在表达LST上NDMI比NDVI更有效；3)综合分析表明，地表水汽特征是其表面温度最主要的影响因素，其次是海拔。研究结果将为山区地表温度空间分异性特征及形成机制的研究提供科学的参考。

地表温度；地形因子；归一化水汽指数；归一化植被指数；泰山

从气候学意义上看，影响温度空间分布的因素主要包括宏观地理条件(经、纬度以及宏观的气候背景条件等)、局地地形条件(海拔、坡度、坡向、遮蔽度等)以及下垫面性质(土壤、植被状况)等[1]。目前在下垫面性质影响地表温度特征的研究较多。地表热特征主要由土壤湿度和植被覆盖确定[2- 3]。因此，许多学者应用植被指数(NDVI)来定量分析地表温度(LST)[4- 5]，并大都发现两者之间存在着明显负相关关系[6- 9]。但不少研究同时发现NDVI在表征地表温度上有其局限性，地表温度与NDVI特征空间有时呈三角形，难以用简单的函数关系加以描述[10- 12]。为了能够更好的量化与表征地表植被特征，有些学者开始探寻新的替代性指标。Wilson[13]在森林管理与采伐的研究中发现应用归一化水汽指数(NDMI)比NDVI指数更容易鉴别出不同的采伐或森林干扰类型。钱乐祥[3]在城市热岛的研究中也发现NDMI比NDVI更适合表达地表热特征。然而，以山区作为研究区比较NDVI和NDMI对地表温度影响的研究目前并不多见。

除了下垫面性质之外，地形也是地表温度的重要影响因素[14- 15]。Bailey[16]研究发现海拔每升高1000 m，温度平均下降6.4 ℃，但这一规律具有地域特征。Wilson[17]指出，除了海拔，地表温度可以表示成纬度、坡度、坡向、地形阴影和时间的函数。因为太阳入射能量对维持地表能量平衡具有重要影响，特别是在地形复杂的地区，影响更加显著[18]。Martin[15]将山区植被冠层温度表示成海拔与太阳入射角的函数，并获得了较理想的结果，为研究地形对地表温度的影响提供了依据。然而，目前国内对于山区地表温度反演及影响因素特征分析的研究还不多见。

本文将以泰山作为研究对象，利用泰山的TM卫星遥感影像数据、ASTGTM2高程数据、MODIS影像，在综合考虑了泰山地区的下垫面特征、局地地形条件、太阳入射能量的基础上，首先分别探讨了每类因子与地表温度的统计学特征，然后利用逐步回归法综合分析了地表温度和归一化指数、地形因子之间的关系，以期为了解山区地表温度空间分异特征及形成机制提供科学的理解与借鉴。

1 研究区概况

泰山是中国五岳之首，主峰玉皇顶海拔1545 m，位于泰安市城北，地理位置117°06′15″E，36°15′17″N。泰山地势差异显著，地形起伏大，总体地势呈现北高南低、西高东低的特征，在不到10 km的水平距离内，玉皇顶与其山前平原相对高差达1300 m以上。泰山的山麓区域气候属于暖温带半湿润大陆季风气候类型，四季分明，夏季炎热多雨，冬季寒冷干燥。气温日、年较差比较平缓，具有高山气候的特点。气温垂直变化明显，山下1月均温-3 ℃，山顶-9 ℃，山下7月均温26 ℃，山顶18 ℃。泰山森林类型主要包括针叶林、落叶阔叶林、针阔混交林等，植被覆盖率90%以上。主要植被种类有麻栎(Quercusacutissima)、栓皮栎(Quercusvariabilis)、刺槐(RobiniapseudoacaciaL)、枫杨(Pterocaryastenoptera)、侧柏(Platycladusorientalis)、油松(pinustabuliformis)、落叶松(Larixgmelinii)、苔草(Carexspp)等。本文选取的研究区位于济南市的历城区、长清区与泰安市泰山区、岱岳区4个市辖区交界处，研究区边界南面基本上与200 m等高线重合，北面沿山谷划定，总面积147.85 km2。

2 数据和研究方法

2.1 数据来源与预处理

2.1.1 数据来源

本文的主要基础数据包括：1)2006年6月19日的Landsat 5 TM影像，条带号122—35，其中TM6热红外波段分辨率120 m，从USGS网站获取时，已被重采样至60 m，其余波段30 m，云量0%；2)MODIS影像，MOD07 L2为MODIS每天的大气剖面数据，空间分辨率为5 km，影像拍摄时间比TM影像晚15 min，大气状况短时间内的影响可以忽略，因此利用MOD07估计单窗算法的大气含水量；3)ASTGTM2 DEM数据，于2011年10月发布的，全球水平空间分辨率为30 m，海拔精度17 m。

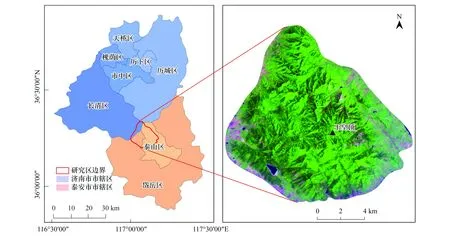
图1 研究区区位图Fig.1 Location of the study area

2.1.2 数据预处理

NDVI与NDMI的物理依据是地物反射率的差异，而TM影像存储的为DN值，所以需要对TM影像进行辐射校正，将DN值转换成真实的地表反射率。MODIS产品原始的投影为正弦投影，本文利用ENVI地理校正工具将投影转换为经纬度投影。海拔数据直接从DEM中提取，坡度和坡向数据由ArcGIS软件生成。由于直射像元接受的辐射量正比于太阳入射角i的余弦值[19]，所以用它的余弦值表示其大小，其计算公式如下[20]：

cosi=cosθpcosθz+sinθpsinθzcos(Φa-Φ0)

(1)

式中,θp、Φ0为坡度、坡向，θz、Φa分别为TM影像拍摄时的太阳天顶角与方位角。θz、Φa可通过查找TM影像的头文件得到，分别为23.58°，116.03°。

所用TM为L1T数据，已经经过了地形校正，并且TM影像与ASTGTM2投影相同，因此，无需再对两者进行匹配，可以直接使用。

2.2 研究方法

2.2.1 地表温度反演

地表温度反映的是传感器在卫星高度观测到的热辐射强度相对应的地面温度[21]。本研究应用TM6的热红外波段并主要根据覃志豪等[22]推导出的单窗算法来反演泰山的地表温度。单窗算法依据地表热辐射传导方程，利用地表辐射率、大气透射率和大气平均温度3个参数推导出的一个简单易行的演算方法，来进行地表温度的演算。大气透过率采用MOD07的大气廓线数据进行估计，其他的演算公式以及参数取值详见文献22，此处不再累述。当基本参数估计没有误差时，演算绝对精度 < 0.4 ℃，当参数有适度误差时，演算精度仍达 < 1.1 ℃[22]。当利用MODIS反演的大气参数应用于TM地表温度反演时，单窗算法的反演精度为0.76 ℃[23]。与1 km的MODIS地温产品相比，通过单窗算法反演的地表温度具有高空间分辨率的优势。将NDVI、遥感影像分类图、TM6波段以及各个参数代入演算公式中，借助ArcGIS空间建模工具，获得研究区的地表温度(图2)。

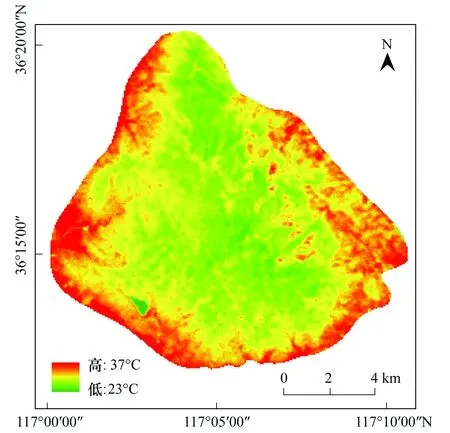
图2 泰山LST空间分布图Fig.2 LST map of Mount Tai

2.2.2 地形因子选取

由于所选研究区属于区域性山脉，因此，只考虑局地地形条件。Martin[15]在研究地形对植被冠层温度影响时，选取了海拔与太阳入射角两个地形因素。Martin研究认为太阳入射角是由坡度、坡向以及太阳高度角、方位角计算得出，因而太阳入射角就包含了这些因素所携带的信息。但是这种做法的科学性值得商榷，因为坡向、坡度是决定植被空间分布的主要原因[24]，而植被可以引起地表温度空间分异，即坡度、坡向可以通过影响地表性质，间接影响到地表温度。而太阳入射角只是反映了栅格单元间所接收太阳入射能量的差异，不能反映地表性质的变化。综合考虑，本文中选定了4个地形因子：海拔、太阳入射角、坡度、坡向。

2.2.3 NDVI与NDMI获取

地表热特征与植被紧密相关，而NDVI是表征地表植被覆盖特征的一种常用的植被指数。因此，NDVI在一定程度上可以反映地表温度的特征。其值域范围[-1,1]，正值对应着植被冠层的密度和绿色，值越大代表植被的覆盖度越高；0代表该区域基本没有植被生长；负值代表非植被覆盖的区域。其计算公式为[25]：

NDVI=(NIR-Rdsat5)/(NIR+dsat5Rdsat5)

(2)

式中，NIR、dsat5Rdsat5表示TM4近红外波段、TM3红光波段。

NDMI是利用近红外与短波红外之间的差异来表达的，与NDVI相比，NDMI与植被冠层水汽含量高度相关[26]，表征地表水汽特征。值域范围[0,1]，高值对应着水汽含量高的植被冠层、水体，低值对应着岩石、建筑物、构筑物等表面水汽含量低的地表物质[3]。其计算公式[27]：

NDMI=(NIR-MIR)/(NIR+MIR)

(3)

式中, MIR表示TM5短波红外波段。

2.2.4 GIS与统计分析

本文选取了两类影响地表温度的因子：地形因子与地表特征指数NDVI、NDMI。首先分别分析这两类因子与地表温度之间的关系，每个因子与地表温度之间的相关程度采用Pearson相关系数来描述。由于很多研究表明水体具有明显的降温效应，往往在地表形成绝对“冷岛”[28- 29]，因此在研究地表温度与地形的关系时，对研究区水体进行了掩模处理，由于研究区像元数太多，为较清晰地反映地形因子与地表温度间的关系，所以采用300 m×300 m渔网采样。NDVI与NDMI都是反应地表特征的指数，由于研究区地表类型分布不均匀，水体较少，使用渔网采样不能较好地反映整体的特征。因此，计算逐像元条件下的LST-NDVI与LST-NDMI的Pearson相关系数，进行对比分析。然后，依据地表温度与每个因子相关系数的大小选取重要因子，与地表温度间进行单独分析。最后综合所有可选因子采用逐步回归分析法构建最优的地表温度回归方程，回归方程中由于变量较多，使用简单相关关系(Pearson相关系数)已不能真实地反映单个因子与地表温度的关系，采用偏相关系数来判断变量的相对重要性[30]。分析统计过程在SPSS软件中实现。

3 结果与分析

为直观地展现泰山地表温度的分布特征，将地表温度反演图与ASTGTM2高程图叠加生成LST随地形变化的三维图 (图3)。

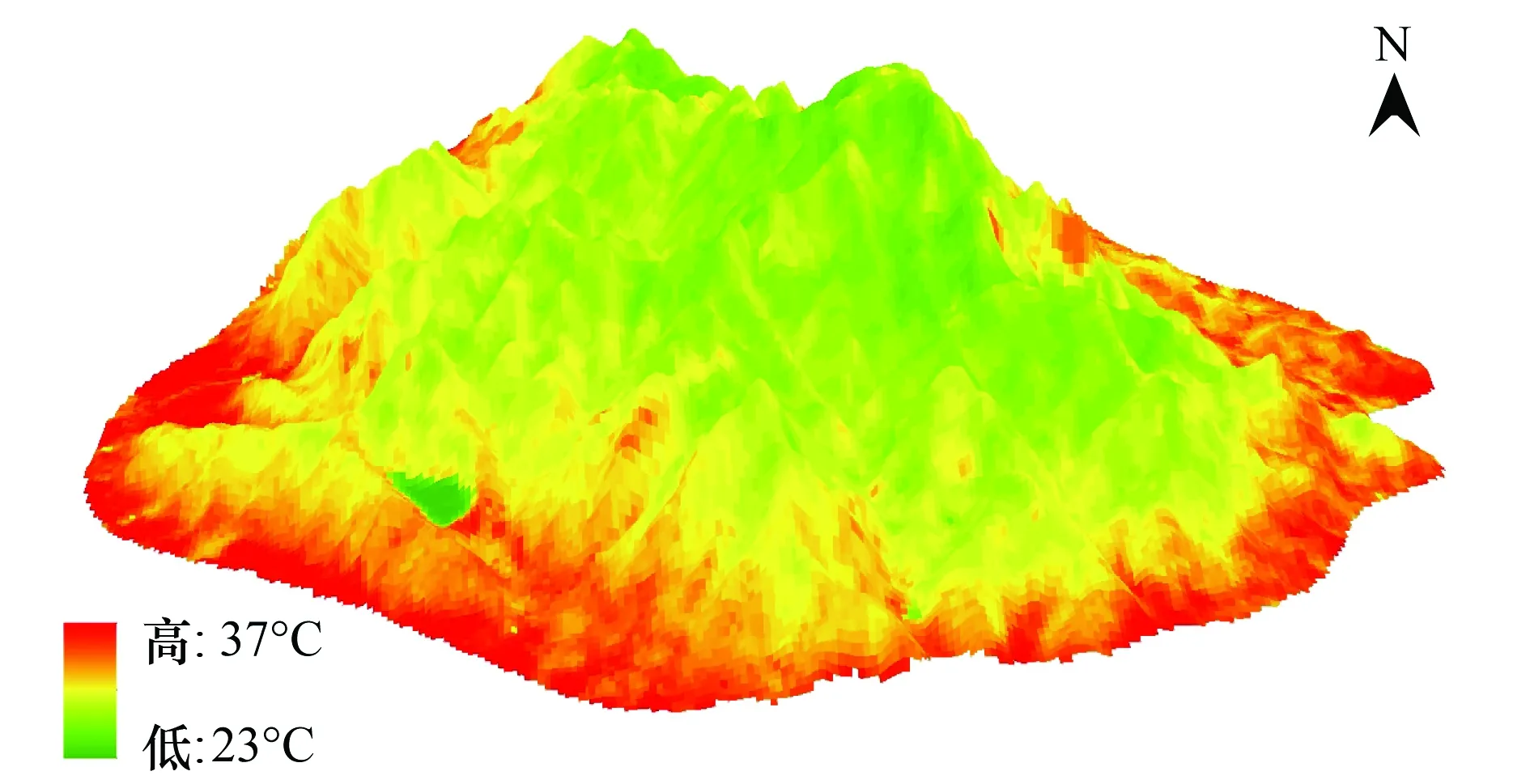
图3 基于DEM的LST三维图Fig.3 The three dimensional map of LST based on DEM

从图3可以看出，由边缘向中心，颜色逐渐由红色向绿色过渡，即地表温度随着海拔呈逐渐降低的趋势。为清晰准确地表示地表温度与地形之间的关系，将基于回归分析，进一步揭示它们之间的统计学规律。

3.1地形、太阳入射能量对地表温度的影响分析

将选定的4个地形因子与地表温度间进行相关分析，分析结果见表1。

从表1可以看出地表温度与坡度之间的相关性强于与太阳入射角(cosi)之间的相关性，这也说明提前剔除掉坡度、坡向因子是不合理的。地表温度与坡向之间的皮尔森相关系数最差，与海拔之间相关性最好。对除水体之外整个研究区用渔网采样后，构建了地表温度与海拔之间的散点图(图4)。

表1 泰山地区地表温度的地形因子间的相关系数

** 在0.01水平(双侧)上显著相关

从图4散点图可以看出，随着海拔的升高，地表温度呈明显的降低趋势。为定量分析地表温度与海拔之间的关系，又对两者进行了线性与自然对数拟合。如图4所示，在海拔低于900 m左右，线性关系能很好地反映两者之间的关系，然而随着海拔继续升高，地表温度随海拔的变化率在逐渐的减小，自然对数的拟合分析整体效果较好。由此，可以得出，地表温度随着海拔的升高，并非是简单地线性降低，而是呈自然对数形式递减。

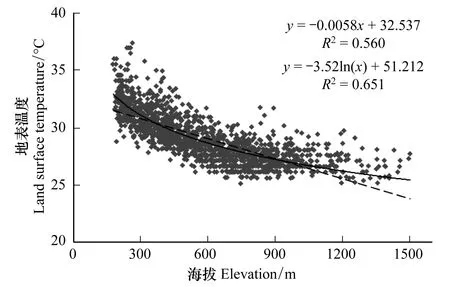
图4 地表温度-海拔的散点图、与线性、自然对数拟合分析Fig.4 The scatter diagrams and regression curves between land surface temperature and elevation

为进一步分析地表温度与地形因子之间的关系，应用逐步回归分析法建立地表温度与地形因子的回归方程，其中海拔取自然对数值，结果如表2所示。

由表2中可以看出，常数及其各变量都通过了T检验，方差膨胀因子VIF都较小，因子间没有多重共线性。由偏相关系数一列，可以得出：地表温度与海拔、坡度间呈负相关关系，与太阳入射角(cosi)、坡度呈正相关关系；影响地表温度的主要地形因素是海拔，坡度、坡向以及太阳入射能量对地表温度影响均非常小。

将表2中的“非标准回归系数”列数据代入多元回归模型得到地形因素影响下的最优的逐步回归模型：

LST=49.399-3.364ln(Elevation)-0.01Slope+ 0.001Aspect+1.12cosiR2= 0.663

(4)

3.2NDVI与NDMI对地表温度的影响

对研究区内的所有像元进行地表温度与NDVI、NDMI的相关分析，Pearson相关系数分别为-0.742、-0.830，说明地表温度与两者之间均存在着高度负相关关系。为直观描述地表温度随NDVI、NDMI的变化规律，进一步统计了LST-NDVI与LST-NDMI的散点图(图5)。

从图5可以看出这两个指数与地表温度的散点图中都存在“离群值点”，不同的是NDVI位于图5的低值处，而NDMI位于图5的高值处。将地表温度图与遥感影像图叠加进行对比，可以发现LST-NDMI之间的“离群点”都是水体纯净像元(图5黑色椭圆实线内)；而LST-NDVI的“离群点”不但包括水体纯净像元(图5黑色椭圆实线内)，还有水体与自然地表混合像元(图5黑色椭圆虚线内)。水体与自然地表的混合像元如图6红色框所示，1个热红外像元包含4个可见光像元。图6中红色框内，NDVI为-0.067，LST为27.81 ℃，处于图5黑色虚线内。另外，由图5还可以看出水体以及水体与地表混合像元的LST与NDVI之间存在着正相关关系，这与梁保平[21]结论一致。

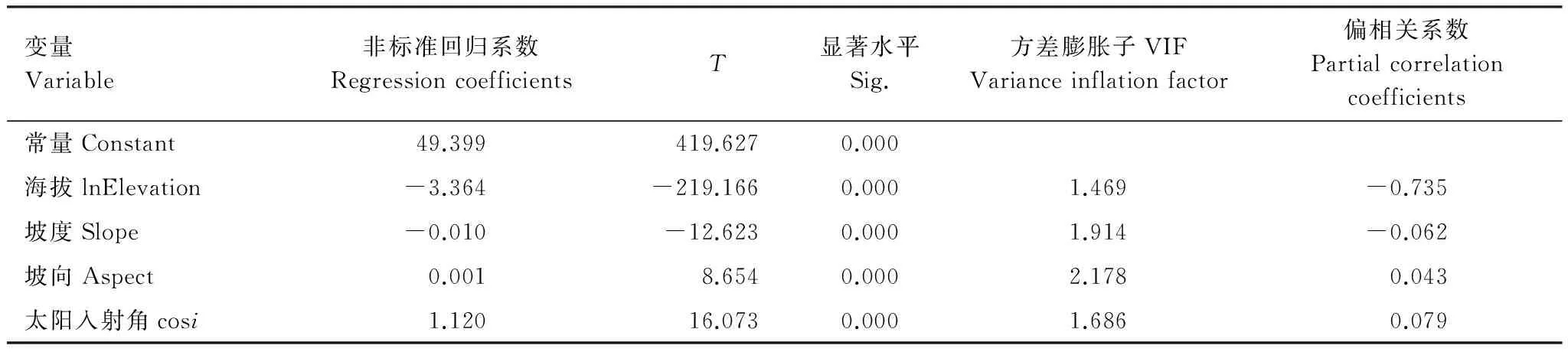
表2 逐步回归分析最终模型的统计量

P< 0.01,R2= 0.663

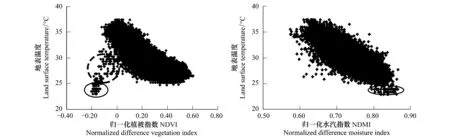
图5 地表温度与归一化植被指数、归一化水汽指数的散点图Fig.5 The scatter diagrams between LST and NDVI, NDMI

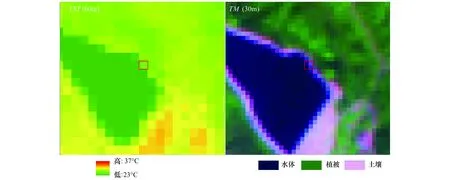
图6 LST (60m)与TM (30m)中近水体混合像元Fig.6 Mixed pixels near the water body of LST (60m) and TM (30m)

对水体进行掩模及排除掉水体与自然地表混合像元后，分别建立LST-NDMI和LST-NDVI的回归方程，结果如图7所示。

由图7可以看出，地表温度与NDVI、NDMI之间都具有良好的负相关函数关系。地表温度与NDVI之间关系是非线性的，随着NDVI的增大，地表温度降低的变化率在逐渐减小，两者之间的最佳拟合为二项式拟合(图7)，这也表明了地表温度在高植被覆盖区(NDVI > 0.5左右)的“饱和”现象[31- 32]。图7显示的地表温度与NDMI的散点图及回归方程可以看出地表温度与NDMI之间呈稳定而简单的线性关系，且复相关系数(R2= 0.691)较地表温度与NDVI(R2= 0.650)之间的高。

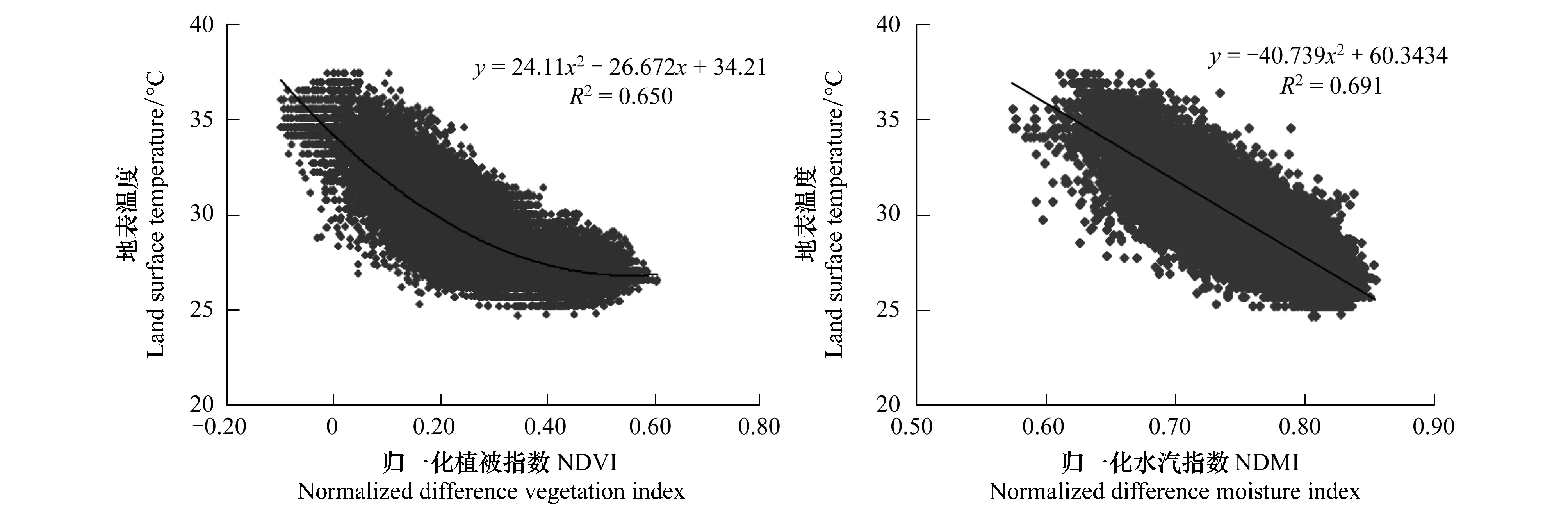
图7 地表温度与NDVI、NDMI的散点图及回归分析Fig.7 The scatter diagrams and regression curves between LST and NDVI, NDMI

综上所述，在山区，当没有水体时，NDVI、NDMI与地表温度均存在着很强的负相关函数关系；当有水体时，NDMI在使用时，需要对水体进行掩模，而NDVI还需要对水体做一定距离的缓冲区，将混合像元也排除掉。NDMI适用范围比NDVI广，且与地表温度的拟合效果优于NDVI。结合钱乐祥[3]平原城市中的研究结果，可以得出在夏季，表征地表水汽特征的NDMI比表征地表植被覆盖状况的NDVI更适合于表达地表热特征。NDVI与NDMI虽然表征的内容上有所不同，但两者之间相关系数为0.783，具有高度的相关性，为避免变量间的共线性问题，因此，选取NDMI作为描述地表性质的参量，参与下面的回归分析。

3.3山地地形地表温度的多因子回归分析

基于以上分析，对研究内水体进行掩模处理后，选取了海拔、坡度、坡向以及太阳入射角和NDMI 5个因子，其中海拔取自然对数，对山区地表温度进行综合分析。统计量如表3所示。

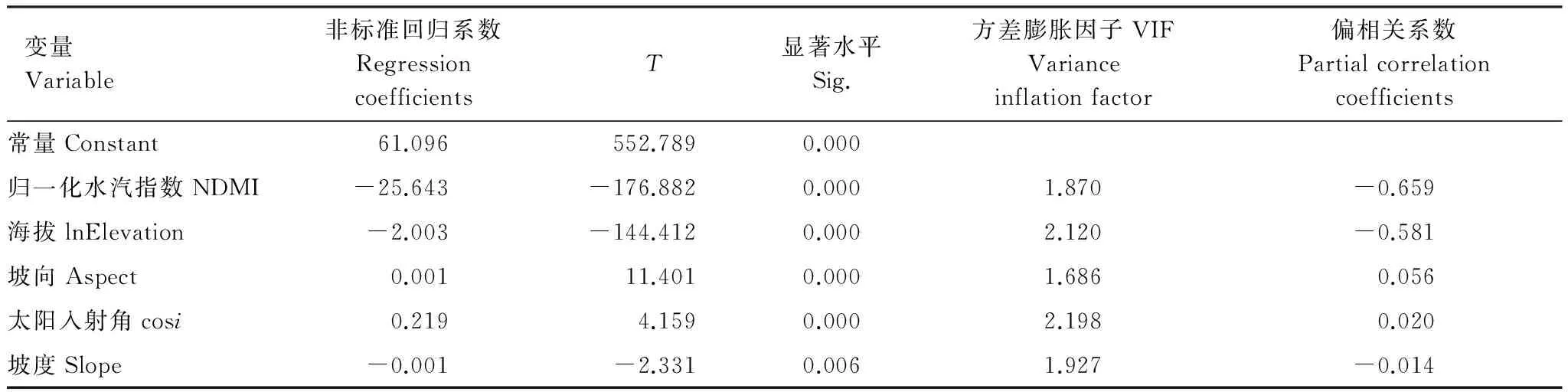
表3 逐步回归分析最终模型的统计量

P< 0.01,R2= 0.809

由偏相关系数一列可以看出，影响泰山山区地表温度的最大因素是地表自身的水汽特征，其次是海拔，且都与地表温度呈显著负相关关系。地表温度与其他3个地形因子间均是弱相关关系。

将表3中的“非标准回归系数”列数据代入多元回归模型得到泰山山区的最优的逐步回归模型：

LST=61.096-25.643NDMI-2.003ln(Elevation)+0.001Aspect+0.219cosi-0.001SlopeR2= 0.809

(5)

4 结论与讨论

本文采用TM6单窗算法，获得泰山山区的地表温度。并应用统计学原理分析地表温度与地形因子和归一化指数(NDVI、NDMI)之间的关系，得到出以下结论：

(1)地表温度随着海拔的升高以显著自然对数形式递减。在地形因子对地表温度影响分析中发现，海拔是地表温度的最大影响因素，而坡度、坡向以及太阳入射能量等局地地形条件的影响均很小。

(2)反映下垫面特性的NDVI与NDMI对地表温度的影响分析发现地表温度与这两个指数都具有良好的负相关关系。但研究也发现NDVI在表征地表温度时，不但要对水体进行掩膜，还要对水体进行一定范围的缓冲区处理，另外地表温度在高植被覆盖区(NDVI > 0.5左右)会出现“饱和”现象。相比于NDVI与地表温度的二次项负相关，NDMI与地表温度的线性负相关更能有效表达地表温度。

基于以上研究可以发现影响夏季泰山山区地表温度的主要因素是下垫面特征，其次是海拔，而坡向、太阳入射角和坡度对地表温度也会产生不同程度的影响。本研究尝试综合考虑地形因素及下垫面特征分析地表温度空间分布差异性的影响因素，研究结果为科学的理解山区地表温度空间格局特征及机制提供一定的参考。整个研究区内的植被覆盖度较高，所得结论在裸地较多的山区是否适用还需单独分析。本文研究区内海拔差异较大，因此采用NDVI估算地表辐射率，会对地表温度的反演结果产生一定影响；除此之外，地表温度还会受人类活动、局地微气象等因素的影响，本研究都没有考虑，这有待于将来进一步研究与探讨。

致谢： 占文凤副教授对本文写作给予帮助，特此致谢。

[1] Weng D M, Luo Z X.Mountainous Terrain Climate.Beijing: Meteorological Press, 1990: 144- 144.

[2] Weng Q H, Lu D S, Schubring J.Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies.Remote sensing of Environment, 2004, 89(4): 467- 483.

[3] Qian L X, Cui H S.Relationship between normalized difference moisture index and land surface temperature.Geographical Research, 2008, 27(6): 1358- 1366.

[4] Peng Z, Liao H P, Guo Y T, Li Q.Influence of land cover change on land surface temperature in the mountainous city.Geographical Research, 2009, 28(3): 673- 684.

[5] Zhou Y, Shi T M, Hu Y M, Gao C, Liu M.Relationships between land surface temperature and normalized difference vegetation index based on urban land use type.Chinese Journal of Ecology, 2011, 30(7): 1504- 1512.

[6] Carlson T N, Gillies R R, Perry E M.A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover.Remote Sensing Reviews, 1994, 9(1/2): 161- 173.

[7] Goetz S J.Muti-sensor analysis of NDVI, surface temperature and biophysical variables at a mixed grassland site.International Journal of Remote Sensing, 1997, 18(1): 71- 94.

[8] Li G D, Wang N A, Zhang J H, Zhao L Q.Urban thermal field and heat island effect of Lanzhou city in summer.Scientia Geographica Sinica, 2008, 28(5): 709- 714.

[9] Deng Y J, Kuang Y Q, Huang N S, Huang J.Remote sensing analysis of urban thermal environment changes under background of enhanced greenhouse effect—An example of Dongguan, Guangdong.Scientia Geographica Sinica, 2008, 28(6): 814- 819.

[10] Price J C.Using spatial context in satellite data to infer regional scale evapotranspiration.IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(5): 940- 948.

[11] Gillies R R, Kustas W P, Humes K S.A verification of the ′triangle′ method for obtaining surface soil water content and energy fluxes from remote measurements of the normalized difference vegetation index, NDVI and surface temperature.International Journal of Remote Sensing, 1997, 18(15): 3145- 3166.

[12] Li H, Liu Q H, Zou J.Relationships of LST to NDBI and NDVI in Changsha-Zhuzhou-Xiangtan Area Based on MODIS Data.Scientia Geographica Sinica, 2009, 29(2): 262- 267.

[13] Wilson E H, Sader S A.Detection of forest harvest type using multiple dates of Landsat TM imagery.Remote Sensing of Environment, 2002, 80(3): 385- 396.

[14] Geiger R, Aron R H, Todhunter P.The Climate Near the Ground.6th ed.Lanham, MD: Rowman and Littlefield Publishers, 2003.

[16] Bailey R G.Ecosystem Geography.New York: Springer Verlag, 1996.

[17] Wilson J P, Gallant J.Secondary topographic attributes // Terrain Analysis: Principles and Applications.New York: John Wiley & Sons, 2000: 87- 131.

[18] Bellasio R, Maffeis G, Scire J S, Longoni M G, Bianconi R, Quaranta N.Algorithms to account for topographic shading effects and surface temperature dependence on terrain elevation in diagnostic meteorological models.Boundary-Layer Meteorology, 2005, 114(3): 595- 614.

[19] Meyer P, Itten K I, Kellenberger T, Sandmeier S, Sandmeier R.Radiometric corrections of topographically induced effects on Landsat TM data in an alpine environment.ISPRS Journal of Photogrammetry and Remote Sensing, 1993, 48(4): 17- 28.

[20] Pierce K B, Lookingbill T, Urban D.A simple method for estimating potential relative radiation (PRR) for landscape-scale vegetation analysis.Landscape Ecology, 2005, 20(2): 137- 147.

[21] Liang B P, Li Y, Chen K Z.A research on land features and correlation between NDVI and land surface temperature in Guilin City.Remote Sensing Technology and Application, 2012, 27(3): 429- 435.

[22] Qing Z H, Zhang M H, Karnieli A, Berliner P.Mono-window algorithm for retrieving land surface temperature from Landsat TM6 Data.Acta Geographica Sinica, 2001, 56(4): 456- 466.

[23] Zheng W W, Zeng Y N.Comparative analysis of two land surface temperature retrieval algorithms based on multi-source remote sensing data.Journal of Geo-information Science, 2011, 13(6): 840- 847.

[24] Jiao C W, Zhao M D, Tang G A, Liu X J, Li X Y.Relationship between vegetation spatial pattern and terrain using GIS techniques—A case study in Yaoxian County of Shaanxi province.Bulletin of Soil and Water Conservation, 2005, 25(6): 19- 23.

[25] Rouse J W Jr, Haas R H, Schell J A, Deering D W.Monitoring vegetation systems in the great plains with ERTS // Third Earth Resources Technology Satellite-1 Symposium-Volume I: Technical Presentations.Washington, D C: NASA, 1974: 309- 317.

[26] Hardisky M S, Klemas V, Smart R M.The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina alterniflora canopies.Photogrammetric Engineering and Remote Sensing, 1983, 48: 77- 84.

[27] Li S Q.The Response of Land Use Change to Moisture and Temperature of Land Surface in Xiangjiang River Basin [D].Xiangtan: Hunan University of Science and Technology, 2012.

[28] Duan J L, Zhang X L.Correlative analysis of the diversity patterns of regional surface water, NDVI and thermal environment.Chinese Journal of Applied Ecology, 2012, 23(10): 2812- 2820.

[29] Sun Z R.Study on the Cooling effect of Urban green spaces in Nanjing City [D].Nanjing: Nanjing University, 2012.

[30] Yang S, Sun G J, He W Y, Zhao H, Li F M, Xiong Y C.Correlation of topographic factors with precipitation and surface temperature in arid and cold region of Northwest China: a case study in Gansu Province.Acta Ecologica Sinica, 2011, 31(9): 2414- 2420.

[31] Huete A, Didan K, Miura T, Rodriguez E P, Gao X, Ferreira L G.Overview of the radiometric and biophysical performance of the MODIS vegetation indices.Remote Sensing of Environment, 2002, 83(1): 195- 213.

[32] Yang X, Wu J J, Yan F, Zhang J.Assessment of regional soil moisture status based on characteristics of surface temperature/vegetation index space.Acta Ecologica Sinica, 2009, 29(3): 1205- 1216.

参考文献:

[1] 翁笃鸣, 罗哲贤.山区地形气候.北京: 气象出版社, 1990: 144- 144.

[3] 钱乐祥, 崔海山.归一化水汽指数与地表温度的关系.地理研究, 2008, 27(6): 1358- 1366.

[4] 彭征, 廖和平, 郭月婷, 李清.山地城市土地覆盖变化对地表温度的影响.地理研究, 2009, 28(3): 673- 684.

[5] 周媛, 石铁矛, 胡远满, 高畅, 刘淼.基于城市土地利用类型的地表温度与植被指数的关系.生态学杂志, 2011, 30(7): 1504- 1512.

[8] 李国栋, 王乃昂, 张俊华, 赵力强.兰州市城区夏季热场分布与热岛效应研究.地理科学, 2008, 28(5): 709- 714.

[9] 邓玉娇, 匡耀求, 黄宁生, 黄江.温室效应增强背景下城市热环境变化的遥感分析——以广东省东莞市为例.地理科学, 2008, 28(6): 814- 819.

[12] 历华, 柳钦火, 邹杰.基于MODIS数据的长株潭地区NDBI和NDVI与地表温度的关系研究.地理科学, 2009, 29(2): 262- 267.

[21] 梁保平, 李艺, 陈可宙.桂林市NDVI、地表温度的地物特征及相关性研究.遥感技术与应用, 2012, 27(3): 429- 435.

[22] 覃志豪, Zhang M H, Karnieli A, Berliner P.用陆地卫星TM6数据演算地表温度的单窗算法.地理学报, 2001, 56(4): 456- 466.

[23] 郑文武, 曾永年.地表温度的多源遥感数据反演算法对比分析.地理信息科学学报, 2011, 13(6): 840- 847.

[24] 焦超卫, 赵牡丹, 汤国安, 刘学军, 李晓印.基于GIS的植被空间格局特征与地形因子的相关关系——以陕西省耀县为例.水土保持通报, 2005, 25(6): 19- 23.

[27] 李少青.湘江流域土地利用变化的地表水热环境响应研究 [D].湘潭: 湖南科技大学, 2012.

[28] 段金龙, 张学雷.区域地表水体、归一化植被指数与热环境多样性格局的关联分析.应用生态学报, 2012, 23(10): 2812- 2820.

[29] 孙振如.南京市城市绿地降温效应研究 [D].南京: 南京大学, 2012.

[30] 杨森, 孙国钧, 何文莹, 赵鸿, 李凤民, 熊友才.西北旱寒区地理、地形因素与降雨量及平均温度的相关性——以甘肃省为例.生态学报, 2011, 31(9): 2414- 2420.

[32] 杨曦, 武建军, 闫峰, 张洁.基于地表温度-植被指数特征空间的区域土壤干湿状况.生态学报, 2009, 29(3): 1205- 1216.

Analysisoffactorsaffectingmountainouslandsurfacetemperatureinthesummer:acasestudyoverMountTai

SUN Changfeng1, KONG Fanhua1,*, YIN Haiwei2, YAN Weijiao1, XU Feng1, REN Yijing2

1InternationalInstituteforEarthSystemSciences,NanjingUniversity,Nanjing210023,China2SchoolofArchitectureandUrbanPlanning,NanjingUniversity,Nanjing210093,China

Most of the previous studies related to land surface temperature (LST) are mainly focused on the investigation of urban heat island; however, little has been done on the mountainous area that are usually far away from cities.In this study, using the Landsat 5 Thematic Mapper (TM) at Mount Tai, firstly, the LST was retrieved based on the Mono-window Algorithm; and then the impacts on the LST from several factors including the topography, normalized difference moisture index (NDMI) and normalized difference vegetation index (NDVI) were analyzed though correlation analysis; accordingly, the regression equation between LST and topographic factors as well as NDMI was developed by stepwise regression analysis, the variable coefficients in the regression equation were interpreted using nonstandard regression coefficient, and then the impact of each factor on LST was quantized by partial correlation coefficient.The results show that: 1) In summer, elevation significantly affects the LST and has a significantly negative natural logarithm correlation rather than a negative linear correlation with it.However, the influence of slope, aspect and incident solar energy is not very significant, LST has a weak correlation with each of them; 2) NDVI and NDMI effectively express LST in mountainous areas if water is absent on surface.LST and NDVI have a negative quadratic correlation.In addition, with the increase of NDVI, the LSTs over areas covered by dense vegetation (NDVI>0.5) will appear a “saturation” phenomenon.Meanwhile, LST and NDMI have a simple but stable negative linear correlation.When compared with NDVI, NDMI is more effective and more applicable at a large scale for the expression of LST；3) The comprehensive analysis shows that land surface moisture characteristic is the main factor affecting the LST, and then followed by the elevation.In comparison with the impacts of these two primary factors, those from the other factors are relatively insignificant.These results will provide important information on the examination of the spatial pattern and mechanism of LST across mountainous areas.

land surface temperature; topographic factors; NDMI; NDVI; Mount Tai

国家自然科学基金资助项目(31170444)；中央高校基本科研业务费专项资助

2013- 10- 31;

2014- 04- 01

10.5846/stxb201310312626

*通讯作者Corresponding author.E-mail: fanhuakong@163.com

孙常峰，孔繁花，尹海伟，闫伟姣，许峰，任怡静.山区夏季地表温度的影响因素——以泰山为例.生态学报,2014,34(12):3396- 3404.

Sun C F, Kong F H, Yin H W, Yan W J, Xu F, Ren Y J.Analysis of factors affecting mountainous land surface temperature in the summer: a case study over Mount Tai.Acta Ecologica Sinica,2014,34(12):3396- 3404.