考虑海底管线初始侧向变形的低阶模态水平向整体屈曲分析

郭林坪，刘 润，闫澍旺

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

自20世纪70年代起海底管线逐步在全球范围内成为海上油气运输的主要手段。在海底管线输送石油和天然气的过程中，需要施加一定的压力并升高温度，温度应力与材料泊松效应的共同作用使钢管中产生附加应力。由于受到地基土的约束作用，管线无法自由变形释放应力，随着管长增加附加应力在管线中不断累积，当其值超过地基土体对管线的约束力时，管线就会发生类似于压杆稳定问题的突然变形而使内部应力得到释放，从而导致管线发生竖直向或水平向的整体屈曲，较大的整体屈曲一方面可能导致管线中的弯曲应力增长，接近或达到钢材的屈服强度，对管线的安全运营造成威胁，另一方面，屈曲变形可能导致管线配重层、保温层结构遭到破坏甚至进水，影响管线的正常使用。

对海底管线水平向整体屈曲的研究国外起步较早。Hobbs［1］基于Ker［2］关于连续铁轨的横向屈曲研究成果推导了理想管线竖直向与水平向屈曲的解析解;Taylor和Gan［3-4］考虑了土抗力在管线发生变形过程中的变化，完善了Hobbs［1］的研究成果，并在随后的研究过程中推导了初始侧向变形管线水平向屈曲的解析解;Taylor和Tran［5］考虑了管线在铺设过程中产生初始侧向变形的情况下，提出海底管线发生竖直向屈曲的解析解;Schotman［6］通过模型实验和数值模拟研究提出了土抗力与管线位移的关系;1999年，Sriskandarajah［7］等人对管线水平向屈曲问题的解析解和有限元分析结果进行了比较，指出了海底管线初始侧向变形的重要性。Preston等［8］通过数值分析提出了在管线上预设膨胀弯的方法以控制水平向屈曲。2004年，Hesar［9］利用Abaqus有限元软件对软粘土中海底管线水平向运动的管土相互作用进行了研究。Burio等［10］通过有限元方法对管土相互作用进行了研究;Peek和Yun［11］研究了浮力对铺设于海床表面管线发生水平屈曲的影响。国内的研究相对较少，2005年，刘润等［12］对温度应力下海底管线屈曲分析方法进行了改进;2008年，刘志刚和孙国民［13］以Hobbs［1］的研究成果为基础，结合工程实例初步探讨了深水高温高压管道的侧向屈曲控制措施。2011年，刘润等［14-15］通过模型试验对发生水平向运动时的管土相互作用进行了分析，揭示了当管线发生水平向运动和轴向运动时土抗力的发挥过程及规律性。王武刚、郭林坪等［16-18］通过对温度应力下海底管线的解析解的研究，结合工程实践对理想海底管线的屈曲规律及管线屈曲的影响因素进行了分析。由此可见关于海底管线水平向屈曲解析解研究已经积累了一定的成果，但如何准确计算管线中的温度应力，揭示管线发生屈曲变形的影响因素及规律性还有待深入探讨。

以具有初始侧向变形的海底管线为研究对象，通过理论分析建立了温压联合作用下海底管线水平向整体屈曲的弯矩平衡方程，得到了具有初始侧向变形的管线发生低阶模态整体屈曲的解析解，进而结合实际工程对影响具有初始侧向变形管线水平向整体屈曲的因素进行分析。

1 管线水平向整体屈曲解析解

1.1 管线的初始侧向变形

海底管线在制造和铺设过程中会因为制造的缺陷或地基土体的原因而产生初始的变形，称之为初始侧向变形，为便于解析解的推导，将管线初始侧向变形形状假定为:单拱侧向变形和反对称双拱侧向变形两种形式，如图1所示。由于描述这种侧向变形与管线屈曲的数学方程变量阶数不大于2，因此统称为低阶侧向变形或低阶变形模式。

图1 初始侧向变形形状Fig.1 Topologies of the pipeline initial lateral deformation

假定单拱初始侧向变形和反对称双拱初始侧向变形的形状与理想管线低阶水平向屈曲变形后的形状相同，且反对称双拱侧向变形的对称点不发生移动。则基于理想管线水平向整体屈曲的解析解［17］，可得单拱侧向变形的表达式如式(1)［4］:

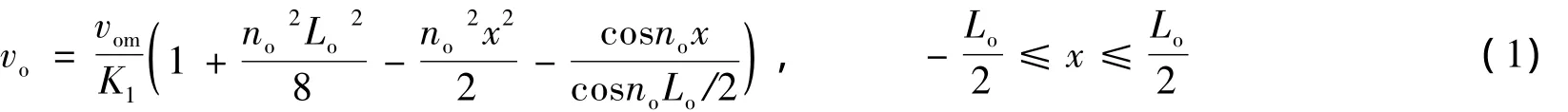
式中:vo为任意位置x处的侧向变形值;vom侧向变形的幅值，vom=2.407×10-3φLqLo4/EI，由理想状态管线屈曲可知vom位于x=0处;K1=15.698 5;Lo为侧向变形的长度;=P/EI，EI为管线的抗弯刚度;P为管线屈曲段内的轴向力。

反对称双拱侧向变形的表达式:

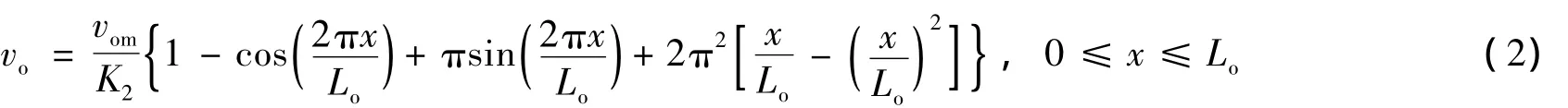
式中:K2=8.621 1;vom=5.531 5×10-3φLq/EI，由理想状态管线屈曲可知vom位于x=0.346 4Lo处;其它符号意义同前。

1.2 具有单拱侧向变形管线的水平向整体屈曲

具有初始侧向变形的管线在温度应力下将在侧向变形处继续发生变形，图2给出了具有单拱初始侧向变形海底管线在温差和压差作用下发生水平向整体屈曲的变形形态和受力分析。

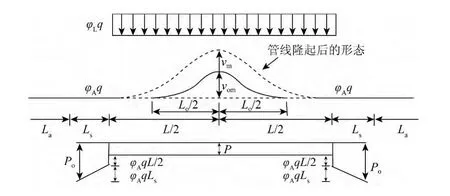
图2 单拱初始侧向变形下管线整体屈曲变形形态及受力分析Fig.2 Deformation and force analysis of the pipeline with one-arch initial lateral deformation

由图可知，发生整体屈曲变形的管线，可根据其变形特点分为如下三个部分:其一为管线的嵌固段，即图中的La段，这部分管线受到地基土体的约束，不发生对地基土体的相对位移，管线内轴力为Po;其二为管线的滑移段，即图中的Ls段，这部分管线没有被地基土全部约束，产生轴向变形释放应力，发生了与地基土体的相对滑动，受到地基土体的摩阻力，摩阻力最大值为φAqLs，其轴力减小，小于Po;其三为拱起段，图中的L段，这段管线在温度和内压作用下，在原有初始侧向变形基础上继续变形，内部压力得到释放减小到Po。

外力对管线所做的功导致管线发生整体屈曲，根据材料力学的基本原理，外力做功可通过应变能V求得。由材料力学中应变能计算方法可知，对于长度为l的杆件，直梁纯弯曲时的应变能为:

式中:I为杆件的惯性矩;E为杨氏模量;M(x)为杆件所受弯矩。

杆件承受外力F拉伸时，杆件的轴向拉伸应变能为:

式中:F为杆件所受轴力;A为杆件的截面积。

图2中管线产生的应变分别来自管线受到的弯矩、轴向的地基土摩阻力和管线内部的轴力，因此管线的应变能为［4］:

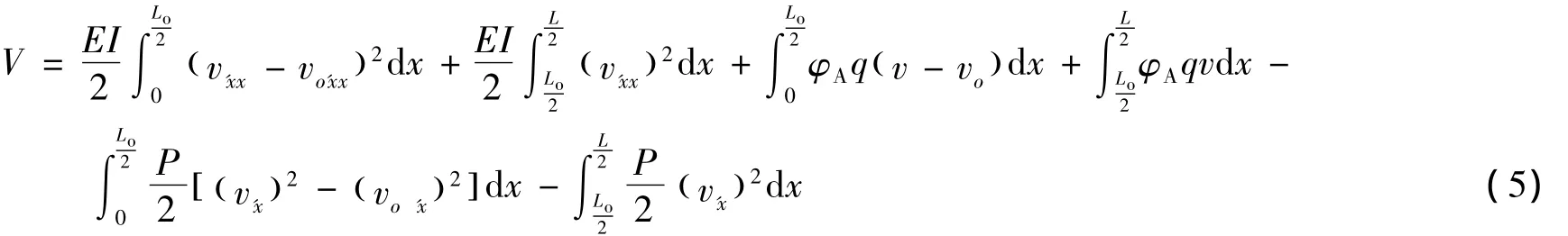
式中:v为任意位置x处的屈曲幅值;vo为任意位置x处的侧向变形幅值;L为屈曲段长度;Lo为侧向变形长度;v’x为管线屈曲变形值对x的一阶导数，vo’x为侧向变形值对x的一阶导数;v’xx为管线屈曲变形值对x的二阶导数，vo’xx为侧向变形值对x的二阶导数;P为屈曲段管线内的轴向力;φA为管线与地基土体的轴向摩擦数;q为管线单位长度重量。

为了确定管线发生整体屈曲的最小温度，需要确定管线发生屈曲的最小应变能。求解dV/dvm=0，可得到屈曲段轴力与屈曲段长度的关系式:

对滑移段进行受力分析，可得到P与Po的关系如下:

式中:Po为温差和压差在管线内产生的轴向力，Ls为管线滑移段长度。

为了进一步建立温度与管线拱起段长度的关系，可将管线内部的压差等效为温差考虑，从而得到:

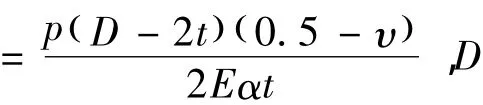
由式(7)、(8)可建立管线所受温差ΔT与屈曲段长度L之间的关系式为:

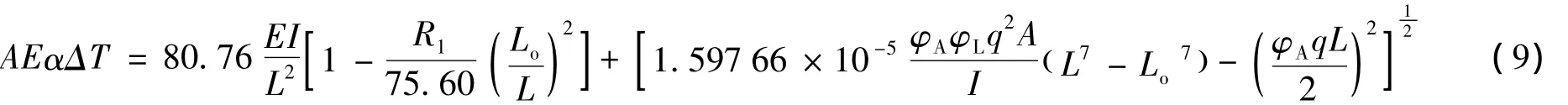
由于管线屈曲长度与幅值是一一对应的，所以由温差ΔT与屈曲长度L的关系可以得到管线的屈曲段幅值vm与温差ΔT之间的关系。

1.3 具有反对称双拱侧向变形的水平向整体屈曲

图3给出了具有反对称双拱初始侧向变形管线在温差和压差作用下发生水平向整体屈曲的变形形态和受力分析。

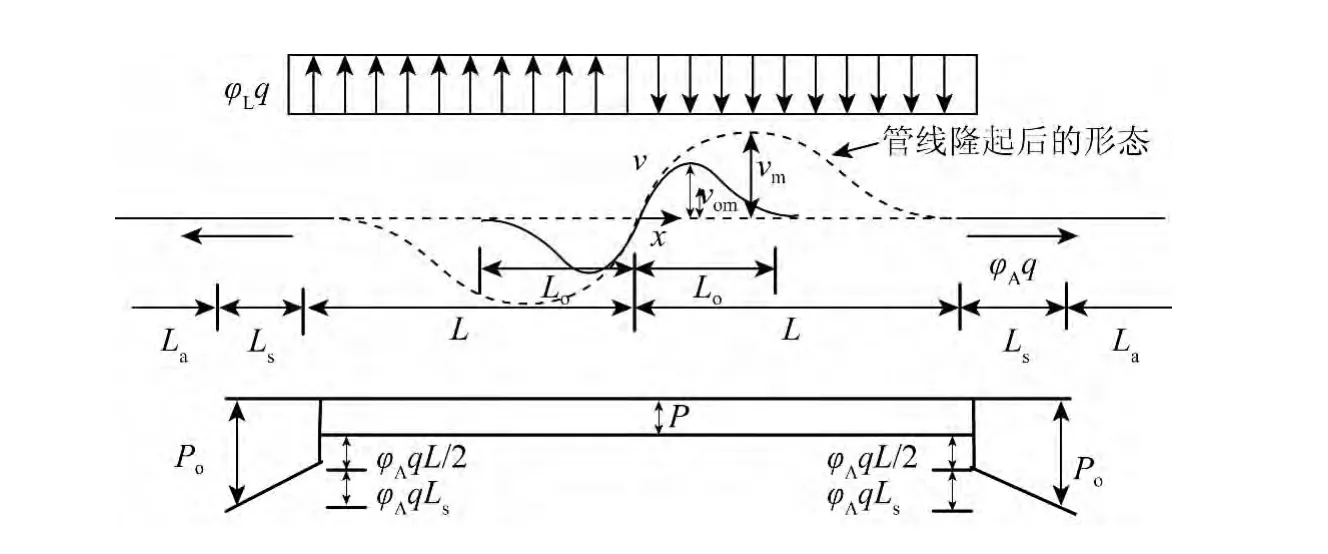
图3 反对称双拱侧向变形下管线整体屈曲变形形态及受力分析Fig.3 Deformation and force analysis of the pipeline with antisymmetry two-arch initial lateral deformation

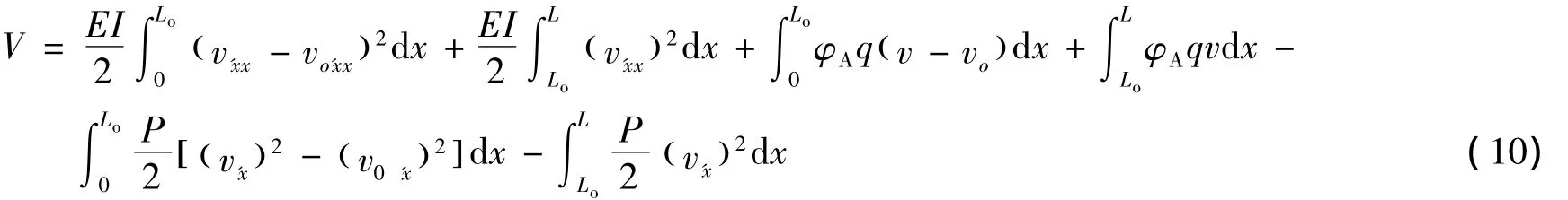
为了确定管线发生整体屈曲的最小温度，需要确定管线发生屈曲的最小能量。令dV/dvm=0，可得到屈曲段轴力与屈曲段长度的关系式:

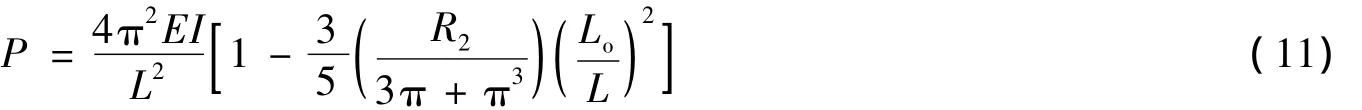
对滑移段进行受力分析，可得到P与Po的关系如下:

通过滑移段的性质可以确定管线屈曲段轴力P与温差ΔT间的关系。结合式(8)、(12)则有温差ΔT与屈曲段长度L之间的关系:

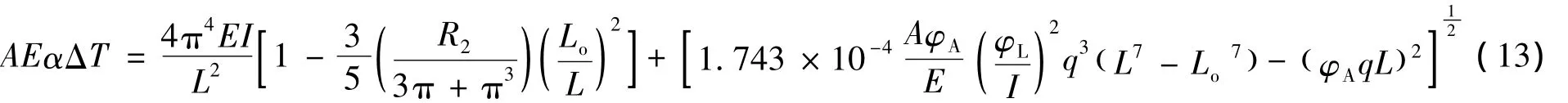
由于管线屈曲长度与幅值是一一对应的，所以由ΔT与L的关系即可建立管线屈曲段幅值vm与温差ΔT之间的关系。

2 工程实例分析

2.1 工程概况

某海底管线外径323.9 mm，壁厚12.7 mm，设计内压为4.60 MPa，设计温度为45°C。表1给出了该管线及地基土体的设计参数。

由于海水的环境温度为20°C，因此设计温差为25°C，由式(8)可知内压的等效温差为5.18℃，因此可以按总温差30.18℃进行计算。采用前述解析方法编程，分析管线在设计温差和压差作用下的水平向整体屈曲规律性。

表1 管线及地基土参数Tab.1 Parameters of pipeline and subsoil

2.2 初始侧向变形对水平向整体屈曲的影响

由表1可估算地基土与管线之间的摩擦系数为0.4。为了分析初始侧向变形对管线水平向整体屈曲的影响，分别假定管线没有初始侧向变形，以及存在初始侧向变形且幅值为100 mm的情况进行对比分析，图4给出了计算得到的温差和管线整体屈曲幅值vm的关系。

图4 温差与水平向整体屈曲幅值的关系曲线Fig.4 Relationship of ΔT vs.vm

由图4可以看出，是否考虑初始侧向变形对管线整体屈曲的特性有较大影响，当不考虑侧向变形存在时管线发生屈曲后幅值与温差的关系曲线成“v”型，而考虑初始侧向变形后曲线呈“r”型;对比图4可知，在考虑初始侧向变形的情况下，初始侧向变形的形状对管线屈曲后的变形亦有一定的影响。各种情况下管线发生整体的初始温差存在差异，计算结果见表2。

表2 管线屈曲温差Tab.2 Initial buckling temperature of the pipeline

可知，不考虑侧向变形情况得到的管线屈曲对应的起始温差均高于考虑侧向变形的情况，而反对称双拱整体屈曲模式对应的管线初始屈曲温差略低于单拱整体屈曲模式的管线。说明了温差和压差相同的条件下，具有初始侧向变形的海底管线较理想状态下的海底管线更容易发生整体屈曲，且具有反对称双拱初始侧向变形的海底管线比具有单拱初始侧向变形的海底管线更易发生整体屈曲。

2.3 初始侧向变形形式对水平向整体屈曲的影响

为了进一步分析初始侧向变形形式对管线水平向整体屈曲变形的影响，假定管线具有相同的初始侧向变形幅值，vom=300 mm，对具有两种初始侧向变形形式的管线分别进行计算，图5分别给出了计算得到的管线屈曲幅值(vm)和屈曲段长度(L)与温差的关系。

图5表明，初始侧向变形形式对管线整体屈曲变形形态有较大的影响，相同的温差下单拱整体屈曲模式的屈曲幅值大于反对称双拱整体屈曲模式的幅值，但屈曲长度小于后者;在相同的初始侧向变形幅值情况下，单拱整体屈曲模式的起始温差为21.72°C，高于反对称双拱整体屈曲模式的起始温差17.87°C，说明在相同的温差下具有反对称双拱初始侧向变形的管线更容易发生整体屈曲。

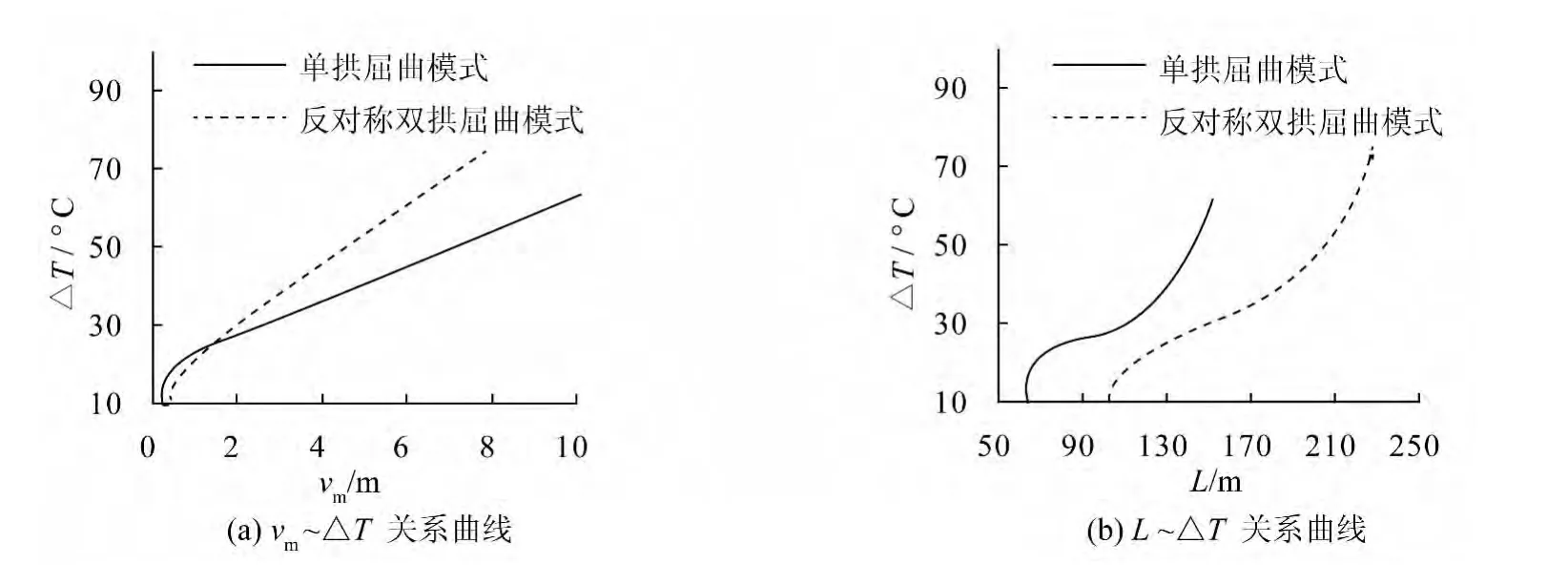
图5 vom=300 mm时管线的水平向整体屈曲规律Fig.5 Relationships of vm～ΔT and L～ΔT with vom=300 mm

2.4 初始侧向变形幅值对水平向整体屈曲的影响

假定管线具有不同的初始侧向变形幅值进行对比分析，图6给出了两种屈曲变形模式下设计温差与管线屈曲变形幅值的关系。

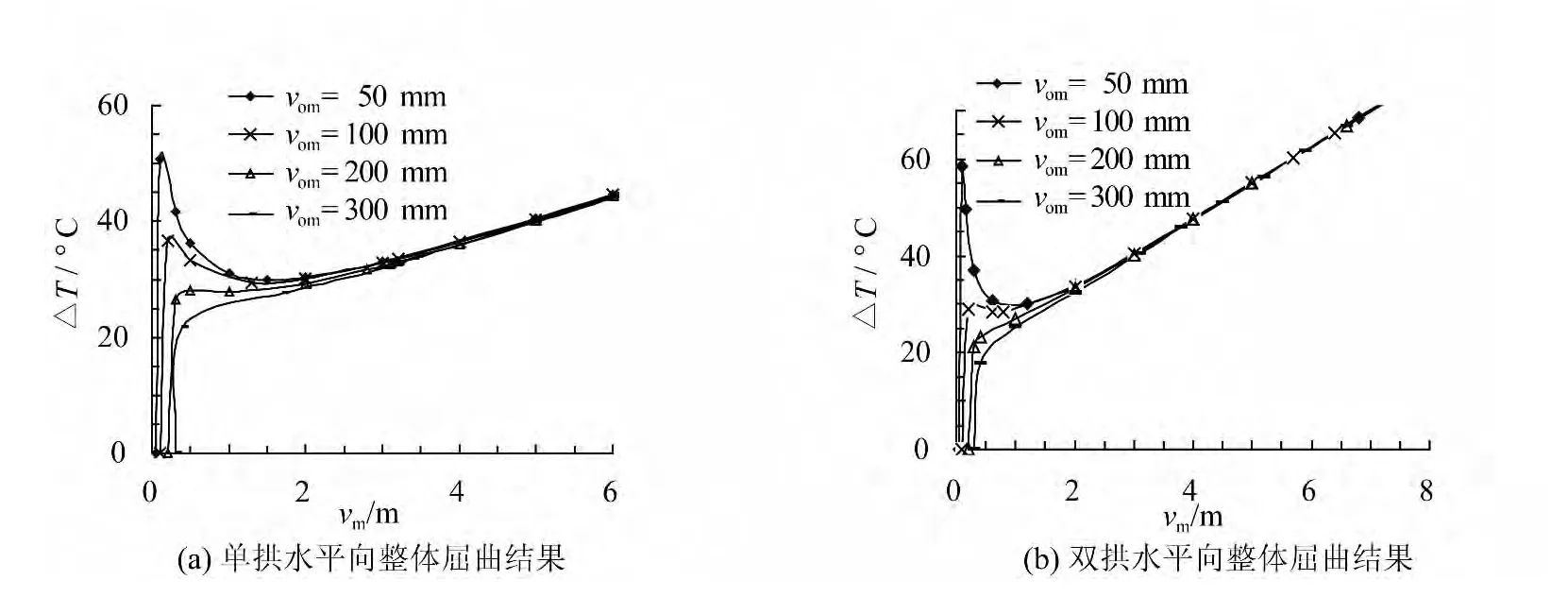
图6 初始侧向变形幅值对管线整体屈曲的影响Fig.6 vm～ΔT loci with the different amplitudes of initial lateral deformation

由图6可知，初始侧向变形幅值越大，管线发生屈曲对应的起始温差越低，说明相同设计条件下侧向变形幅值越大的管线越容易发生整体屈曲。无论管线具有哪种形式的初始侧向变形，随着侧向变形幅值的增大，vm～ΔT关系曲线的形态发生变化，即在较小初始侧向变形情况下，例如vom＜200 mm，曲线上出现极值点，管线屈曲段幅值呈现随温差增加先下降后上升的情况，表明管线的变形存在不稳定阶段，可由曲线的左半支跳跃达到右半支，出现突然性的大变形;而当初始侧向变形的幅值增加到达200 mm以上后，vm～ΔT关系曲线上的极值点消失，即管线的屈曲变形幅值随着作用温差的增加而持续增长，跳跃段消失。

2.5 地基土约束力对水平向整体屈曲的影响

当温度和压力一定时，土体对管线的约束力大小决定了管线是否发生整体屈曲［15-16］。对于不进行挖沟埋设的海底管线，管土间的摩擦力是土体对管线的唯一约束力，因此摩擦力对管线屈曲特性有着重要的影响。假定管线具有的初始侧向变形幅值不变(vom=50 mm)，只改变管土之间的摩擦系数进行分析。图7为摩擦系数取φ=0.01，0.10，0.20，0.30，0.40情况下，计算得到的管线屈曲幅值与设计温差和管线轴向压力的关系。

由图7中的vm～ΔT关系曲线可知，无论是哪种形式的初始侧向变形，管线发生水平向整体屈曲的幅值随着设计温差的增大而增大，管线发生整体屈曲对应的起始温度随着管土间摩擦系数的增加而升高，即地基土对管线的约束力越大，管线越不易发生屈曲;图7中的Po～ΔT曲线表明，随着管土间摩擦系数的增大，对于发生相同幅值屈曲的管线，引发屈曲的轴向压力亦增大。这都表明摩擦系数的增大会使得管线更加安全。

由以上计算分析可知，无论是否考虑初始侧向变形，该工程中的管线在温差为31.8°C的设计条件下都存在发生整体水平向屈曲的可能;由于第二种管线屈曲比第一种更易发生，因此计算了管线发生第二种屈曲时管线中的最大轴向压应力，为167 MPa，而对于工程中使用的管线，其屈服应力为448 MPa，因此，管线虽然会屈曲，但并不会屈服破坏。

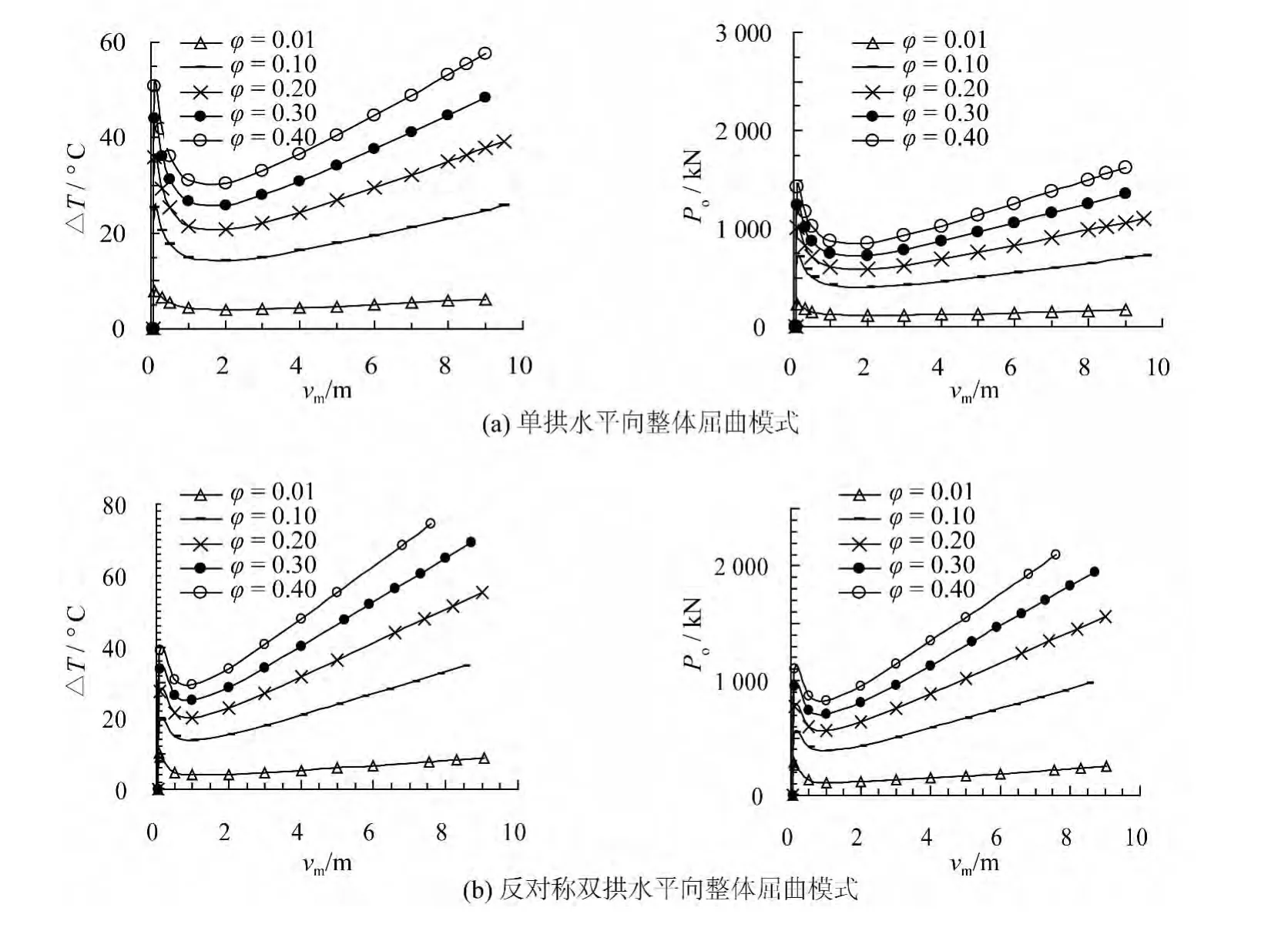
图7 不同摩擦系数下管线水平向整体屈曲的特征曲线Fig.7 vm～ΔT loci with different pipe-soil friction coefficients

3 结语

建立了温压联合作用下，具有初始侧向变形的海底管线发生单拱或反对称双拱模式水平向整体屈曲的解析解，结合工程实例分析了初始侧向变形的存在、变形形态和幅值以及地基土体约束对管线水平向整体屈曲的影响，可得到以下结论:

1)初始侧向变形对管线的水平向整体屈曲有较大的影响。无初始侧向变形的管线屈曲后vm～ΔT关系曲线呈“v”型，而考虑初始侧向变形存在时，得到的管线整体屈曲vm～ΔT关系曲线呈“r”型，相同设计条件下具有初始侧向变形的管线更容易发生整体屈曲。

2)管线所具有的初始侧向变形形式影响管线的整体屈曲形态，当初始缺陷幅值相同时，反对称双拱屈曲模式较单拱屈曲模式更容易发生。

3)管线所具有的初始侧向变形幅值的大小对其整体屈曲的vm～ΔT关系曲线形状有较大影响。当初始侧向变形较小时(例如算例中初始侧向变形值小于200 mm时)，vm～ΔT关系曲线上出现极值点，说明管线会发生不稳定变形，出现变形的跳跃阶段，但随着初始侧向变形幅值的增加，这种不稳定变形现象消失;相同设计条件下初始侧向变形幅值越大的管线越易发生整体屈曲。

4)管线受到的地基土摩擦力对其整体屈曲的vm～ΔT关系曲线形状影响较小，但显著影响管线发生整体屈曲的起始温度和屈曲后管线内的轴力大小。随管土间摩擦系数的增大，管线发生整体屈曲的起始温差提高，对于发生相同幅值整体屈曲的管线，引发屈曲的轴向压力亦增大，表明增大土体对管线的约束力可以提高管线抵抗整体屈曲的能力。

［1］ Hobbs R E.In service buckling of heated pipelines［J］.Journal of Transportation Engineering，1984，110(2):175-189.

［2］ A D Kerr.Analysis of thermal track buckling in the lateral plane［J］.Acta Mechanica，1978，30:17-50.

［3］ Talor N，Gan A B.Refined modeling for the lateral buckling of submarine pipeline［J］.Journal of Constructional Steel Research，1986，6(2):143-162.

［4］ Talor N，Gan A B.Submarine pipeline buckling-imperfection studies［J］.Thin-Walled Structures 4，1986:295-323.

［5］ Neil Taylor，Vinh Tran.Prop-imperfection subsea pipeline buckling［J］.Marine Structures 6，1993:325-358.

［6］ Schotman G J M.Pile-soil interaction:A model for laterally loaded pipelines in clay［C］//Offshore Technology Conference.1987:317-324.

［7］ Sriskandarajah T，Dong S，Sribalachandran S，et al.Effect of initial imperfections on the lateral buckling of subsea pipe［C］//Proceedings of the International Offshore and Polar Engineering Conference.1999，2:168-175.

［8］ Preston R，Drennan F，Cameron C，et al.Controlled lateral buckling of large diameter pipeline by snaked lay［C］//Proceedings of the Ninth International Offshore and Polar Engineering Conference.1999:58-63.

［9］ Hesar M.Pipeline-seabed interaction in soft clay［C］//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering.2004，3:225-233.

［10］ Nelly Piedad Burio，Deane Roehl and Celso Romanel.A three dimensional contact model for soil-pipe interaction［J］.Journal of Mechanics of Materials and Structures，2007，2(8):1501-1513.

［11］ Peek R，Yun H.Flotation to trigger lateral buckles in pipelines on aflat seabed［J］.Journal of Engineering Mechanics，2007，133(4):442-451.

［12］刘 润，闫澍旺，孙国民.温度应力下海底管线屈曲分析方法的改进［J］.天津大学学报，2005，38(2)，124-128.(Liu Run，Yan Shuwang，Sun Guomin.Improvement of the method for marine pipeline upheaval analysis under thermal stress［J］.Journal of Tianjin University，2005，38(2)，124-128.(in Chinese))

［13］刘志刚，孙国民.海底管道侧向屈曲分析［J］.中国造船，2008，49:516-522.(LIU Zhigang，SUN Guomin.Analysis on the lateral buckling of submarine pipelines［J］.Shipbuilding of China，2008，49:516-522.(in Chinese))

［14］ Run LIU，Linping Guo，Shuwang Yan ，et al.Studies on soil resistance to pipelines buried in sand［C］//Advanced Materials Research.Switzerland:Trans Tech Publications，2011:243-249.

［15］刘 润，闫澍旺，王洪播，等.砂土对埋设管线约束作用的模型试验研究［J］.岩土工程学报，2011，33(4):559-565.(Liu Run，Yan Shuwang，Wang Hongbo，et al.Model tests on soil restraint to pipelines buried in sand［J］.Chinese Journal of Geotechnical Engineering，2011，33(4):559-565.(in Chinese))

［16］ Wang Wugang，Liu Run，Yan Shuwang，et al.Vertical upheaval buckling of submarine buried heated pipelines with initial imperfection［J］.Transactions of Tianjin University，2011，17(2):138-145.

［17］ Linping Guo，Run Liu.High-order lateral buckling analysis of submarine pipeline under thermal stress［J］.Transactions of Tianjin University，2012，18(6):411-418.

［18］ Guo Linping，Liu Run，Yan Shuwang.Global buckling behavior of submarine unburied pipelines under thermal stress［J］.Journal of Central South University，2013，20(7):2054-2065.