超大型原油储罐大角焊缝处应力分析及结构优化
2014-10-11张雪铭浙江省天正设计工程有限公司杭州310012
张雪铭浙江省天正设计工程有限公司 杭州310012
由于大型原油油罐在节约钢材、占地面积以及便于规模化管理等方面有着不可取代的优势,因此随着我国原油战略储备计划的开展,油罐的大型化成为一种必然趋势[1]。大型油罐大角焊缝处应力分布极其复杂并且应力水平很高,为油罐危险部位之一,此处的应力分布及应力水平的研究意义重大。
大角焊缝处应力分布与焊缝型式(包括焊角高度、焊缝圆角等方面)、边缘板厚度、边缘板内伸以及外伸长度、第一圈壁板(从下往上计数,以下同)、焊缝质量以及焊接材料与工艺等方面有着密切的关系。本文利用大型有限元计算软件ANSYS,分析焊角型式、边缘板厚度、边缘板内伸及外伸长度等对大角焊缝处应力水平的影响,以期对国内超大型原油储罐的设计和工程建设给予参考意见和指导性作用。
1 油罐结构及有限元计算方案
某台超大型原油储罐根据API 650标准,采用变点法设计[2],内径110 m,罐体整体高度23.04 m,设计储液高度21.1 m;最下面五圈壁板采用APQ490,第一圈壁板厚度44 mm,罐底边缘板厚度24 mm,焊角高度13 mm。罐体整体呈轴对称结构,因此基于减小计算规模的考虑,采用二维轴对称单元PLANE183建立二维轴对称模型。工程建设过程中,大型油罐一般采用钢筋混凝土环梁地基,即在罐壁下方底板处设置具有一定宽度的钢筋混凝土环梁,环梁内部铺设沙垫或者泥土层[3]。进行有限元分析时,将变形可忽略的钢筋混凝土环梁视作刚性,拟采用接触单元模拟罐底与地基之间的耦合。将环梁内部地基视为弹性地基,同时省略刚性环梁,并约束边缘板最外侧节点竖向位移,形成所谓“半接触”[4]。有限元计算模型见图1,大角焊缝处单元划分细节见图2。
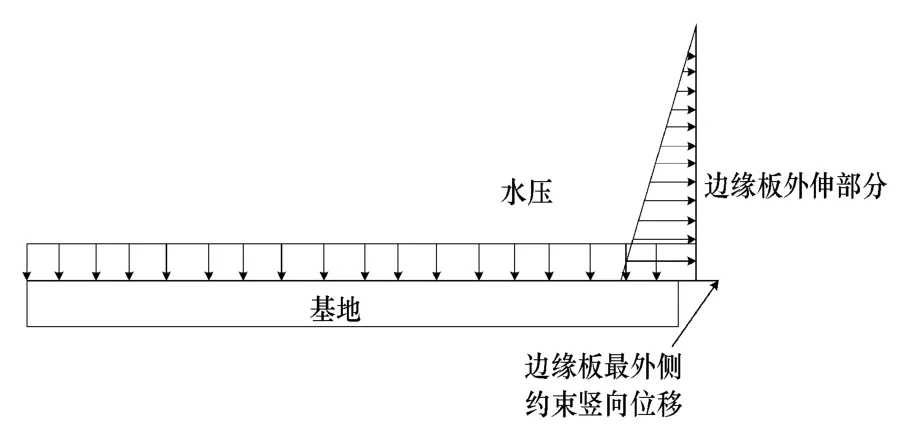
图1 有限元计算模型示意图

图2 大角焊缝处结构
图3给出了大角焊缝处应力强度分布云图。
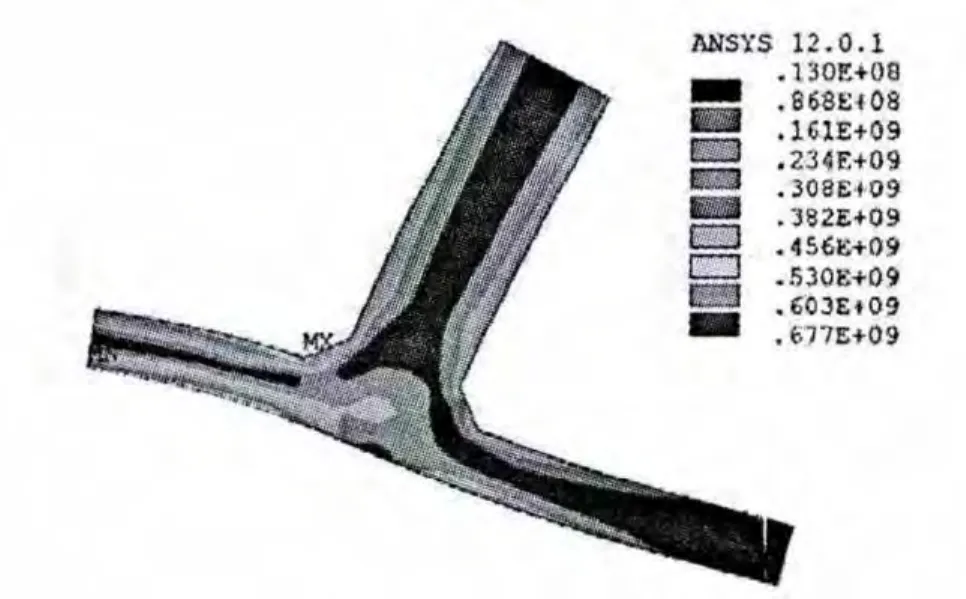
图3 大角焊缝处应力强度分布云图
由图3可知,应力强度最大值为677 MPa,位于大脚焊缝内侧,并且迅速衰减。为了更好的分析应力分布,按照JB 4732-1995要求取路径进行应力分析,见图2。沿路径1及路径3进行应力分类,得出路径1上薄膜应力SI为19.7 MPa,薄膜应力+弯曲应力SII最大值为161.7 MPa,位于罐壁内侧;路径3上薄膜应力SI为38 MPa,薄膜应力+弯曲应力SII最大值为464.1 MPa,位于边缘板上侧,应力沿路径分布曲线见图4。由此,在大脚焊缝处,虽然峰值应力很高,但大部分由弯矩造成,由液压引起的薄膜应力占很小一部分。这是由于此处结构的不连续造成了应力分布的复杂性,因此可以考虑从结构入手来尽量减小峰值应力。
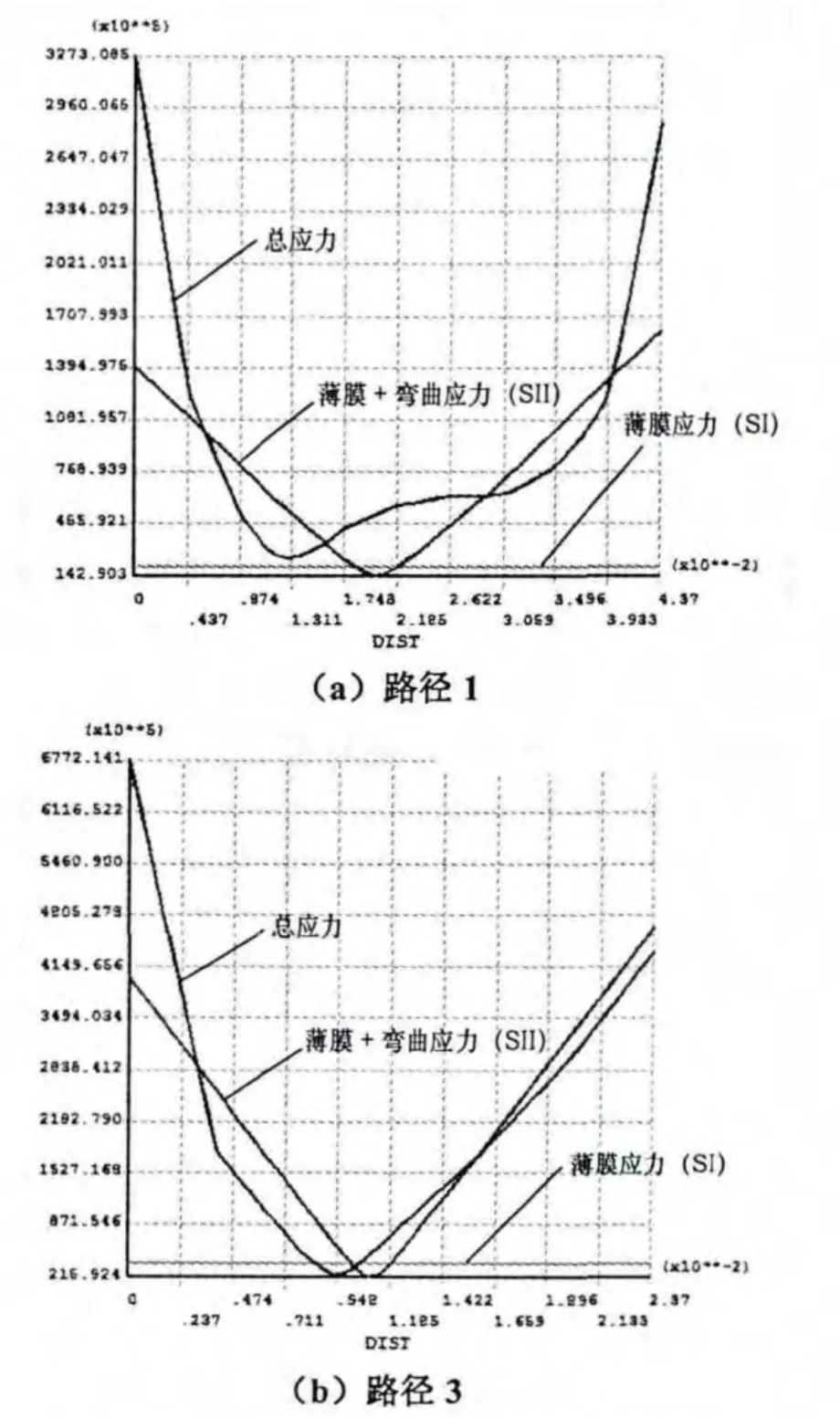
图4 路径上应力沿厚度方向分布曲线
2 大角焊缝的结构优化
由于大角焊缝为结构不连续处,存在较大的应力集中,因此可以通过更改大角焊缝处结构来进行缓和。本文依次分析了增加焊角高度、内侧焊角打磨圆角及延长内侧焊缝尺寸等方面对于峰值应力的影响。
(1)单纯增加焊角的宽度以及高度对峰值应力的影响并不明显,大角焊缝处仍存在较大的应力集中,应力强度值仍然很大。而且浪费焊材并且增加了焊接难度,因此13 mm的焊高已足够,不推荐继续增加;
(2)将内侧焊角打磨圆角之后,由于减小了结构的不连续,因此应力会有下降,并且随着圆角直径在一定范围内的减小,大角焊缝处的最大应力值一直下降。当焊缝打磨圆角15 mm时,大角焊缝处应力强度最大值为604 MPa(见图5),较未打磨圆角前的应力值减小73 MPa,减小10.8%。建议圆角半径在15~20 mm。

图5 内侧焊角打磨半径15 mm圆角后应力强度分布云图
(3)按GB 50341-2003中推荐的焊角型式,在大型原油储罐建设中可以考虑延长罐壁内侧焊缝,且延长距离约为边缘板厚度的两倍。按图6结构建立有限元模型,计算水压工况下的应力强度分布,最大应力值由之前的677 MPa(图3)减小到466 MPa,下降幅度非常明显,减小30%。因此可以综合考虑焊接的技术难度及成本,决定是否延长内侧焊缝长度,以达到减小峰值应力、增强焊缝强度的目的。
3 储罐结构参数对大角焊缝处峰值应力的影响
3.1 边缘板厚度
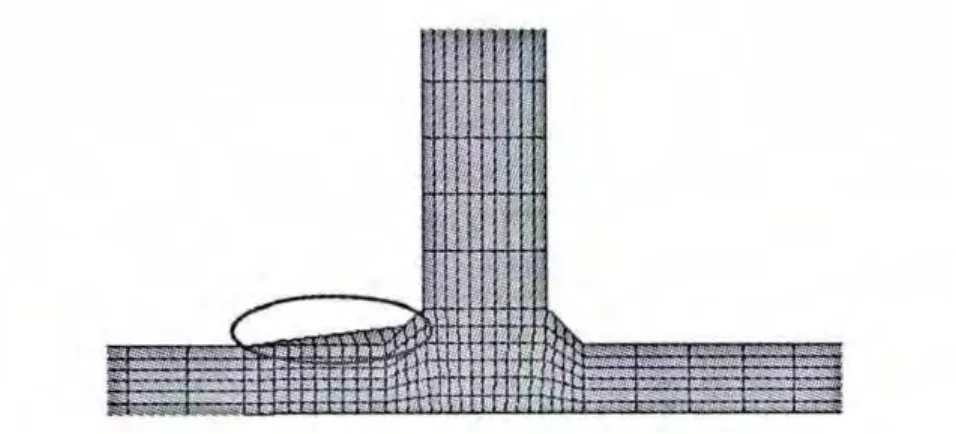
图6 延长内侧焊缝尺寸结构有限元单元
保持储罐其他结构参数不变,将边缘板厚度从18 mm依次变化到27 mm,依次计算不同边缘板厚度储罐充水试验工况下的应力分布。结果表明,应力强度最大值仍然出现在大角焊缝内侧,且最大值随着边缘板厚度的增加而减小。然而边缘板厚度的增加,会造成储罐材料成本及建造难度的增加,因此不宜通过大幅度增加边缘板厚度来减小大角焊缝处峰值应力。边缘板厚度可以取为22~24 mm。
3.2 边缘板外伸长度
边缘板伸出罐壁外侧的长度对于峰值应力的大小会有一定的影响,各国的储罐标准都规定了储罐应存在一定的外伸长度。本文计算了外伸长度由80 mm依次变化到200 mm水压试验工况下的应力分布,见图7。
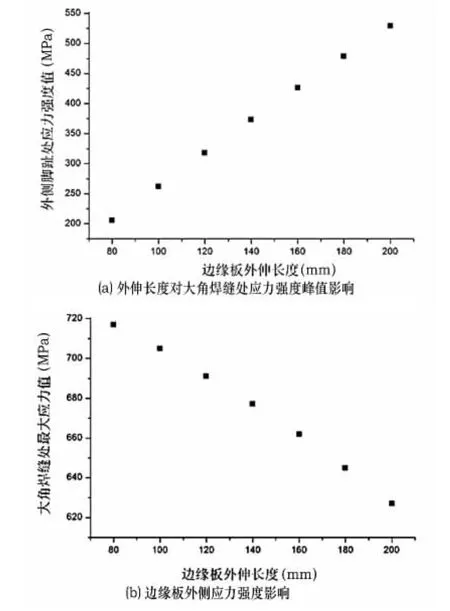
图7 边缘板外伸长度对大角焊缝处应力强度的影响
由图7线可以看出,大角焊缝处的应力强度最大值由外伸80 mm时的717 MPa一直减小到外伸200 mm时的627 MPa,这表明,一定的边缘板外伸长度有利于大角焊缝处应力的释放以及罐底边缘板的翘起。不过随着边缘板外伸长度的增加会使边缘板弯曲程度增大,在罐壁外侧与边缘板焊接处的应力强度也持续增加,因此外伸长度并不能一直增加下去。本文认为,外伸长度可以取为120~140 mm。
3.3 边缘板内伸长度对于大角焊缝处峰值应力的影响
由于储罐受液压之后罐底处会发生一定翘起,即边缘板会发生较大的弯曲。因此,当边缘板内伸长度小于150 mm时,储罐应力强度最大值没有出现在大角焊缝处,而是出现在了边缘板与中幅板对接处(图8为边缘板内伸长度为80 mm时大角焊缝处应力强度分布云图,可以看出应力强度最大值出现在边缘板与中幅板焊接处),应力强度最大值从边缘板内伸80 mm的623 MPa减小到内伸150 mm时的555 MPa,此后储罐整体应力强度的最大值才出现在了大角焊缝内侧,并且随着内伸长度的增加,应力强度值略有增加,后趋于稳定,内伸500 mm时边缘板宽度与地基刚性环梁宽度接近,因此应力状况处于过渡过程。此后大角焊缝处应力不再变化。笔者认为边缘板内伸长度应取环梁宽度2倍为宜。即1.2 m左右。再多的内伸所起作用不大。

图8 边缘板内伸80 mm大角焊缝处应力强度分布云图
4 未焊透对大角焊缝处峰值应力的影响
超大型原油储罐壁厚都较厚,因此不可避免的存在未焊透现象,上文所述水压试验工况下的应力分析并未考虑未焊透的影响。假设在罐壁中间有26 mm厚未焊透,见9(a),其余有限元建模条件同上;图9(b)给出了大角焊缝处的应力强度分布云图,由图可以看出,通过改变未焊透部分的尺寸,计算未焊透部分范围16~36 mm,应力峰值并未出现较大范围的变化。图10给出了路径2上(即边缘板上侧部分)应力强度路径分布曲线,可以看出,罐壁部分(中间约40 mm部分)应力分布较平稳,且应力水平较低;焊角处(两侧各约15 mm)应力变化剧烈;若存在未焊透,则在未焊透处存在应力不连续,应力强度变化出现多次峰值。
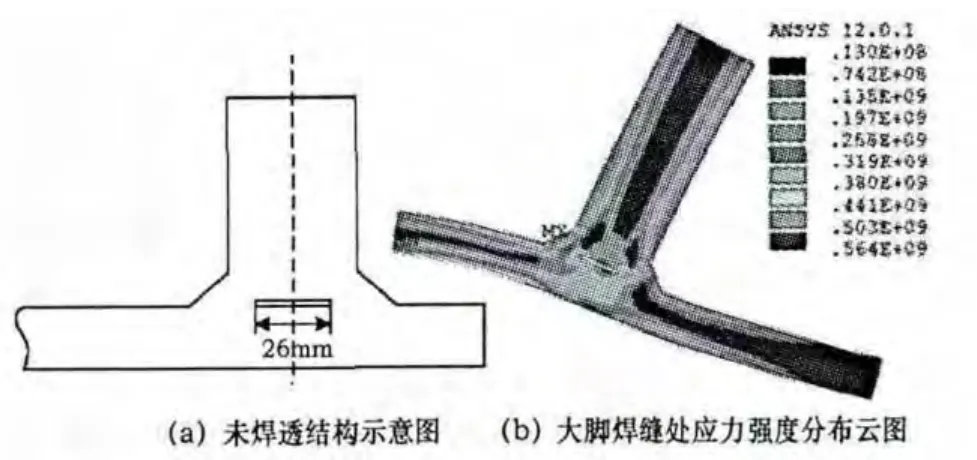
图9 未焊透对储罐应力影响分析
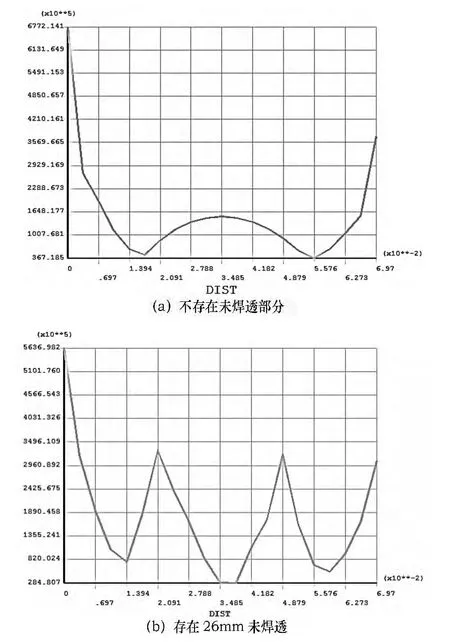
图10 路径2上应力强度分布对比
5 结语
(1)超大型原油储罐大角焊缝处应力强度值很大,为储罐危险部位之一,大角焊缝处应力主要由结构不连续和应力集中引起,为二次应力。
(2)可以通过将储罐内侧焊缝打磨圆角、延长内侧焊缝等手段减小大角焊缝处应力强度峰值,效果明显,但增加了制造成本。
(3)可以通过选择合适的储罐结构参数,包括边缘板厚度、外伸及内伸长度等方式减小大角焊缝处峰值应力。
1 武铜柱.大型立式油罐发展综述[J].石油化工设备技术,2004,25(3):56-59.
2 American Petroleum Institute.API 650-2007 Weld steel tanks for oil storage[S].Washington,DC:API Publishing Services,2007.
3 周丽芳,沈士明,郑 斌.基于地基影响下的大型原油储罐的数值模拟分析[J].炼油技术与工程,2004,38(2):58-61.
4 陈志平.大型非锚固储油罐应力分析与抗震研究 [D].浙江大学,2006.
5 JB 4732-1995,钢制压力容器-分析设计标准[S].全国压力容器标准委员会,北京,中国标准出版社,1995.
6 GB 50341-2003,立式圆筒形钢制焊接油罐设计规范[S].北京:中国计划出版社,2003.
