基于禁忌表算法的传感器管理

张勇 ZHANG Yong

（包头职业技术学院电气工程系，包头 014030）

（Department of Electrical Engineering，Baotou Vocational&Technical College，Baotou 014030，China）

0 引言

在真实战场态势环境中，复杂而多变的动态环境对传感器的数量和传感器与传感器之间的协同都提出来很高的要求。因此，当有多个传感器同时进行目标检测、目标识别和目标跟踪时，传感器和目标之间的任务分配问题，都是亟待解决的问题。本文采用与禁忌表结合的粒子群算法，来分析无人机寻求目标进行最优配对的问题。

1 粒子群算法流程

在任务分配的求解问题中，变量的取值是离散的，所以是非连续的优化问题。在利用粒子群算法进行优化时，必须进行变量的离散化：一方面需要将粒子的位置离散化，另一方面也要将更新速度离散化。因此粒子在选择新位置的时候，并不是在全定义域内进行选择。粒子移动的位置就表示为该粒子对于任务分配的结果，目标的数目也是微粒的维数，粒子的更新速度为无人机和目标之间的任务配对的变化情况。根据约束条件要求，任意目标只能有一个无人机对其发生作用，任一无人机至多也只能对一个目标执行任务，因此在粒子群算法的寻优过程中，微粒各维的最终位置应该是互异的，在本文中采用多次迭代的方法，直到各维变量的位置都不同的时候，才继续往下执行，具体的算法流程如图1所示。①运行开始，进行相关参数的初始化设置（比如设置最大迭代次数等）；②随机对微粒进行初始化设置，即：无人机和目标的任务配对，并计算目标评价函数；1）依次对每一个目标分配一个无人机来执行作战任务，如果无人机和目标的任务分配出现了同一个无人机对两个不同的目标执行任务时候，在重新分配，直到此类情况不再出现（不重复原则）。2）当每个微粒满足任务分配，进行微粒初始值评价；③对微粒进行新速度的计算，并加以限幅；④对微粒进行新位置的计算，并加以限幅；⑤如果微粒处于新位置时，出现微粒对于无人机和目标的任务分配出现步骤②中1）的情况时，重新执行步骤③和步骤④，直到满足要求；⑥按目标评价函数，重新评价各微粒的适应值；⑦对每个微粒，找出微粒个体或群体的最优值；⑧更新所有微粒，并将最优解保存为该微粒的全局历史最优任务分配；⑨若满足终止条件，搜索停止，输出搜索，否则，返回③继续搜索；⑩gbest就是搜索到的最优值。利用粒子群算法来对传感器和目标进行分配从本质上说，就是使得变量中的每一维参数都不同，在这种情况下来获得最大的效用。根据速度更新公式，在粒子每维变量速度的更新公式中，速度的变化量取决于随机数的取值，当出现该维变量与其他维变量取值相同时，最直观的想法就是持续更新随机数，来改变速度变量，从而实现变量取值的目的。因此，有必要对粒子群算法进行改进，从而来得到适合于求解传感器与目标分配效用函数的解决算法。

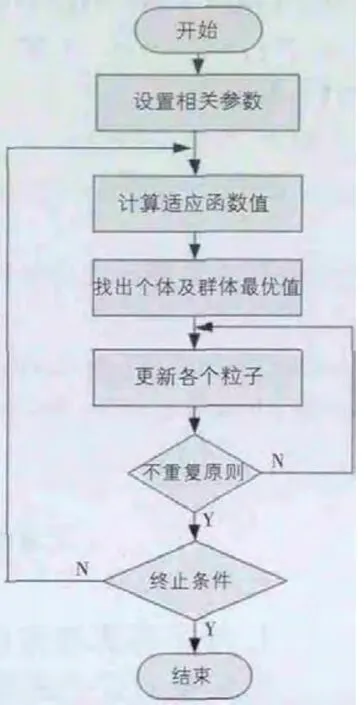
图1 粒子群算法流程图

2 与禁忌表结合的粒子群算法

除了上述的更改粒子更新速度的方法以外，我们还采取了控制粒子选择域的方法来实现传感器与目标的配对。这里，采用了禁忌表的方法。

禁忌表算法是一种全局性邻域搜索算法，禁忌搜索的思想最早由Fred Glover（美国工程院院士，科罗拉多大学教授）提出，它是对局部领域搜索的一种扩展，是一种全局逐步寻优算法。禁忌表的主要目的是阻止搜索过程中出现循环和避免陷入局部最优，它通常记录前若干次的移动，禁止这些移动在近期内返回。结合禁忌表对粒子群算法进行改进：每个微粒的变量都一次来进行速度和位置的更新。值域中被选择过的取值被推入禁忌表，之后的变量在取值时，只能在未被推入禁忌表中的值域中进行选择，因此随着变量的依次取值，值域在不断变小。这样可以避免出现变量取值相同的情况。与禁忌表的粒子群算法流程图如图2所示。它解决了当微粒变量的取值最优解时，由于变量取值的改变程度有限，进入死锁状态，而不能得到最优解。

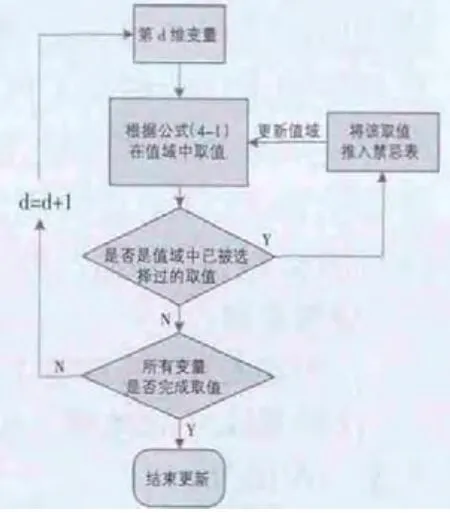
图2 与禁忌表结合的粒子群算法流程图

3 仿真结果

为了验证无人机传感器与目标间的配对问题，与禁忌表结合的粒子群算法是可行的。故假设出6个目标，分别是 （200，12）、（250，12）、（300，12）、（350，12）、（400，12）、（450，12），把目标3作为无人机没办法识别的目标，把目标4作为已经被无人机击毁的目标，其余目标作为无人机攻击的真目标。现将无人机的飞行方向改为从与x轴正向呈负65度开始，以一度的差值依次递减。经过多次计算得到的结果为：第25号无人机对第一个目标执行攻击任务，即25号无人机上的力学传感器对第一个目标进行力学参数测量：第32号无人机对第二个目标执行攻击任务，即第32号无人机上的力学传感器对第二目标执行力学参数测量；第35号无人机对第三个目标执行再识别任务，即第35号无人机上的目标识别传感器对第三个目标执行识别任务；第38号无人机对第四个目标执行毁伤评估的任务，即第38号无人机上的威胁评估传感器对第四个目标进行威胁判断；第40号目标对第五个目标执行攻击任务，即第40号无人机上的力学传感器对第五个目标进行力学测量；最终的效益函数适应值为1.187。

一共做了30次试验，每次试验要完成100次迭代。如图3所示，图中BPSO为基本粒子群算法，TPSO为与禁忌表结合的粒子群算法。图中为两种算法寻求最优值和收敛情况的仿真结果。很好的将与禁忌表结合的粒子群算法和基本的粒子群算法，进行无人机传感器进行目标识别中收敛情况进行比较。

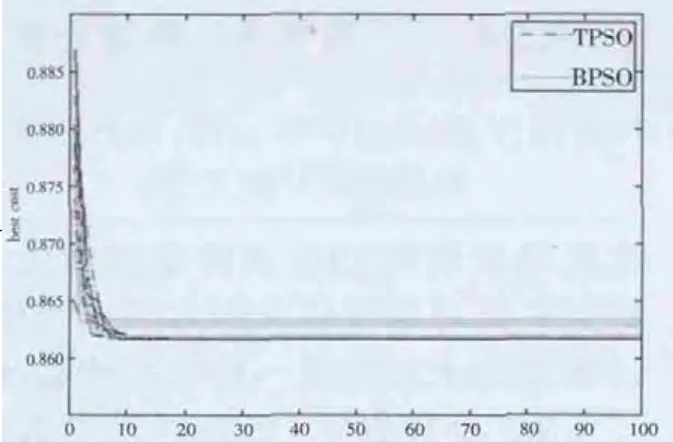
图3 两种算法的的最优值和收敛情况

表1 两种算法的优化结果

从表1中得出如下结论，采用BPSO算法，通常进行30次试验，其收敛的成功率只达到46.7%，并且无法寻找到最优值。采用TPSO算法，同样进行了30次试验，其收敛成功率达到100%。但是在试验的平均耗时角度分析，BPSO算法耗时较少。TPSO算法耗时略有些长。总之，采用与禁忌表结合的粒子群算法，对于无人机传感器管理问题，可以得到很好的解决。其收敛的成功率为100%，虽然在寻求最优配对时，耗时略长，但从搜索成功率的角度看，与禁忌表结合的粒子群算法是可以采用的。

[1]王欣.多传感器数据融合问题的研究[D].吉林大学,2006.

[2]李琪.传感器管理及研究进展[J].科技信息(学术研究),2008(28).

[3]张玉芳,薛青松,熊忠阳.基于禁忌搜索的动态粒子群算法[J].计算机工程与应用,2008(24).