三维集成电路中的关键技术问题综述
2014-10-08王高峰赵文生
王高峰,赵文生
(杭州电子科技大学射频电路与系统教育部重点实验室,浙江杭州310018)
0 引言
CMOS集成电路发展至今,传统二维平面集成工艺已达集成密度极限,为了提升芯片性能,集成更多晶体管,就必须增加芯片尺寸,而芯片尺寸增加带来全局互连距离的延长,从而引发了更严峻的互连问题。要克服互连线带宽限制,必须实质性地改变设计方法。三维集成电路(3-DIC)是传统二维集成电路从平面集成方式向垂直方向立体集成方式的延伸[1]。具体地说,三维集成电路不同于二维CMOS集成工艺只有单个有源层,而是具有多个有源层在垂直方向堆叠,信号主要是应用硅通孔(Through-Silicon Via,TSV)结构进行传输,使不同分层的器件在最短路径上实现了全局互连,从而令在二维大规模集成电路中达毫米甚至厘米长度的全局互连线缩短至100 μm以内!因此,TSV被认为是三维超大规模集成电路的一种最佳解决方案[2]。本文简要论述了三维集成电路所面临的机遇和挑战,并针对三维集成电路的设计自动化的发展趋势进行了展望,并着重详细介绍和评述了三维集成电路中的关键互连技术——硅通孔(TSV)结构的电路建模方法及其发展趋势。
1 机遇与挑战
三维集成电路的机遇与挑战如表1所示。三维集成电路的优势在于[3]:
1)多层器件重叠结构使芯片集成密度成倍提高;
2)TSV结构使互连长度大幅度缩短,提高传输速度并降低了功耗;
3)重叠结构使单元连线缩短,并使并行信号处理成为可能,提高了芯片的处理能力;
4)多种工艺,如 CMOS、MEMS、SiGe、GaAs“混合集成”,使集成电路功能多样化;
5)减少封装尺寸,降低设计和制造成本。
同时,三维集成电路也面临着极大挑战:
1)采用三维工艺后,有源器件集成密度的大幅提升促使芯片功耗剧增,加之芯片内部使用的电介质填充材料导热性能不佳,种种不利因素使得三维集成电路芯片散热问题雪上加霜;
2)采用晶圆对晶圆接合技术时,三维集成电路的产量得到提高,但成品率随之显著减少;
3)三维集成电路中TSV间距远远小于传统系统级封装模具中输入/输出端口的间距,这使得很难针对三维集成电路中的TSV进行有效测试;
4)三维集成工艺中的每一步都会对最终成品率产生影响,需要在三维集成技术大规模生产前对这些工艺问题开展进一步探索;
5)为了充分发挥三维集成技术的优势,我们还需要发展新的设计方法。

表1 三维集成电路的机遇与挑战机遇
2 物理设计自动化
简单的将二维物理设计方法扩展进行三维集成电路确实设计出可以使用的电路。在传统二维集成电路领域,只需要考虑二维坐标不产生重叠即可。然而在三维布图布局中,除了需要处理只分布于一个有源层的标准单元外,还需要处理特殊设计的跨越多个有源层的三维设计模块。这种2.5维的设计方法受二维研究方法本身的限制,无法充分发挥三维集成电路物理结构上的优点而获得更优的设计[4]。因此,在三维集成电路物理设计自动化的研究中,需充分考虑三维集成电路的结构特点,以充分发挥三维结构在互连延迟等方面带来的好处,并减少其结构所带来功率密度、散热、良率等方面的负面影响,从而保证芯片的可靠性和高性能。
在三维集成电路物理设计中,需要将每一个模块表示成为一个三维的立方体,在z轴上有一个固定高度,此时不能使用常规的二维表示方法,必须使用新的表示方法。常用的数据结构有三维划分树、三维角块链以及序列三元组等。当调整模块高度时,需要从候选库中选择最优的模块配置以满足优化过程中的要求,常用的数据结构在空间结构表达不够灵活,所以发展出新的更加灵活的三维模块数据结构至关重要,并且是制约物理设计自动化算法的关键因素。
在设计出灵活的三维数据表示方法后,即可基于该数据结构完成三维集成电路物理设计自动化算法设计。除研究布图、布局、布线在增加z轴坐标后约束条件描述外,还需要发展对物理设计运算时间和求解质量有着关键影响环节的新算法。在布图中需要注意到多目标之间的制约关系,找到适用于三维集成电路设计的最佳平衡点并应用于算法实践;在布局中需要运用新的数据结构设计出更高效率的去交叠算法,例如通过标准单元的旋转来获得更好的布局结果;在布线中需要注意到局部拥塞问题,建立将布线设计阶段的运算结果重新输入布图、布局阶段的反馈机制,从而经过少量迭代实现局部拥塞的控制,并将该反馈机制进一步扩展获得系统级的布通率、热分布、时序约束等方面的共同优化结果。
此外,三维集成电路具有远大于二维集成电路的功率密度,其电源网络设计面临更大挑战,同时其热问题也将成为布图、布局、布线等物理设计步骤必须考虑的内容。必须针对这两方面进行深入研究,发展低功耗电源网络优化方法以及热驱动的物理设计方法。
热效应分析的关键是提高仿真精度和仿真速度,缩短仿真时间,实现对三维集成电路发热和散热情况的快速、准确评估。现在国内外常见的三维集成电路热效应分析方法有以下3种:
1)简单解析模型法[5]。这种模型假定三维集成电路的每层芯片产生的热量是独立而且均匀的,仅考虑三维集成电路在纵向上的热阻及热传导特性,因此这种模型比较简单,呈一维热阻网络形式。这种模型虽然精度不高,但计算速度快,可以粗略估计整个芯片的热分布。这种简单的解析方法可以用于设计流程早期、当芯片的详细物理信息不可知时,为后续过程中更准确的分析和设计提供必要的估算,用来考虑封装、散热及整个芯片系统的设计策略和成本控制;
2)紧凑温度模型法[6]。与平面集成电路不同,三维集成电路中温度梯度和热传导率是各向异性的,在各个方向上都具有不同的分量。紧凑温度模型根据这一关键特性,将芯片产生的功率和热传导通过三维热阻网络来进行描述,将芯片分成局部细区块,以多个传导热阻值表示节点的三维方向关系,以矩阵方式计算节点温度,利用三维热阻网路分析芯片的温度分布,其计算精度优于解析模型的粗略估计。这种方法可以较快得到芯片内部的温度分布情况,便于设计者适当调整发热区块位置,得到最佳的芯片层级散热效果;
3)基于网格计算的温度分析法[7-8]:这种模型基于有限差分法或有限元法等网格计算方法,可以提供高精度的三维集成电路热分析。基于网格计算的热学模型的主要优点是精度非常高,可以适应任何复杂的芯片物理结构和功率密度不均匀的区域,并且网格自身的划分也可以具有复杂几何形状而不依赖于问题的边界条件。这种方法的缺点在于计算量较大,较为耗时。因此该方法适合用来对芯片内的精细结构和关键位置进行详细而准确的分析,实现高精度的优化设计。
针对三维集成电路热效应仿真与热管理方面的研究,目前存在的主要问题是:缺乏精确的热特性建模技术和高效的数值仿真方法。热分析模型虽然计算效率高,但如何保证其准确性?数值仿真虽然精确,但算法效率和硬件资源开销往往让设计者们难以接受,如何提高数值方法的仿真效率?这些问题都将是在今后一段时间内三维集成电路的研究热点。
3 硅通孔技术
最后,本文将详细介绍三维集成电路的关键互连技术——TSV技术。
TSV最早是由诺贝尔奖得主William Shockley提出,如图1所示,即穿过硅衬底的垂直互连,它可以由铜、钨、多晶硅甚至碳纳米管束构造。图2给出了硅通孔的工艺流程:首先将晶圆磨薄至所需厚度,利用反应离子刻蚀法制作通孔;采用低温等离子增强化学气相沉积法在通孔侧壁制造绝缘层,将通孔底部焊垫氧化层去除,使之露出金属层;最后在通孔中填充金属导体,并将晶圆背部多余部分移除[2,11]。特别地,对于铜硅通孔,为了防止铜原子扩散到硅衬底中,还需要在铜与绝缘层间加入一层Ta、Ti或TiN,其厚度约为几十纳米。

图1 (a)由Shockley最早提出的硅通孔概念[9];(b)由IMEC加工得到的硅通孔[10]
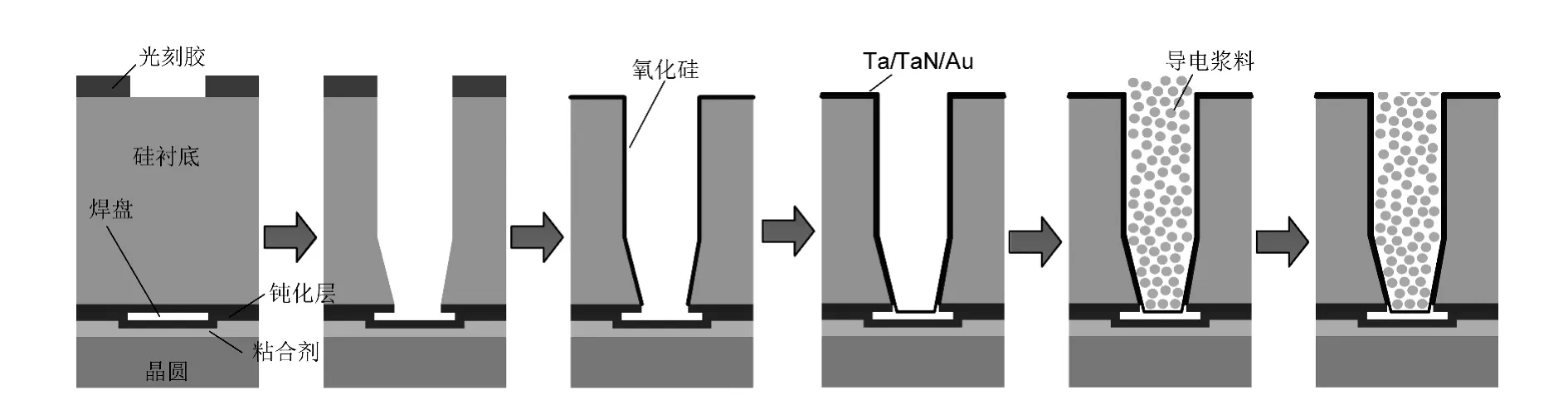
图2 硅通孔的加工流程示意图[2]
硅通孔建模和仿真目前主要有3种方法:基于数据拟合或经验公式的方法、基于准静态模型的方法和基于全波电磁仿真的方法。基于全波电磁仿真的方法,通常根据元器件的内部结构、材料特性和载流子动力学机制,采用有限元法、矩量法及时域有限差分等数值方法对互连结构离散建模后求解Maxwell方程[12-14],该方法精度高,仿真结果可行,缺点是效率低,仿真时间太长,主要用于关键结构的仿真,而不适于全芯片参数提取。
准静态模型方法一般从Maxwell方程出发求解电参数,基于准静电场或准静磁场假设对电磁方程进行简化求解,从而使仿真速度得到极大的提升[15-16]。在电磁辐射可以忽略不计时准静态模型是准确可靠的,但当工作频率上升到接近10 GHz时,三维集成电路互连线电磁辐射成为建模中必须考虑的对象,此时必须对准静态模型进行修正,计入辐射电阻的影响,否则会产生较大误差。
无论是全波电磁仿真还是准静态模型都需要消耗巨大的计算资源,仿真所需时间也很漫长,难以直接应用于三维集成电路的在线快速优化设计中。为了缩短仿真周期,三维集成电路建模亟需与电路仿真工具SPICE网表格式兼容的硅通孔互连结构宽带模型。通过对电磁仿真工具提取的S参数进行拟合发展出的宽带模型(或经验公式)既能满足应用频率范围内互连线仿真精度要求,又具有解析模型的高效特性,从而成为硅通孔建模和仿真的热门研究领域。
针对硅通孔的建模方法已有一些初步研究成果,以其物理原理为基础,根据内部结构、材料特性和物理机理,从电磁特性的基本方程(如泊松方程、电流连续方程、传输方程等)出发导出其数学模型或等效电路[18-25]。图3给出了同轴硅通孔及其等效电路模型,需要注意到硅通孔在径向上为金属-氧化层-半导体(Metal-Oxide-Semiconductor,MOS)结构,其寄生电容受偏置电压影响[10]。由于同轴硅通孔的自屏蔽效应,最外层的寄生电容可忽略不计,从而简化为传输线模型。文献[25]给出了同轴硅通孔电阻、电感参数的解析公式,如图4所示,相较于以前的电阻、电感提取公式可以更加准确地计算其散射参数。

图3 同轴硅通孔及其等效电路模型[17]
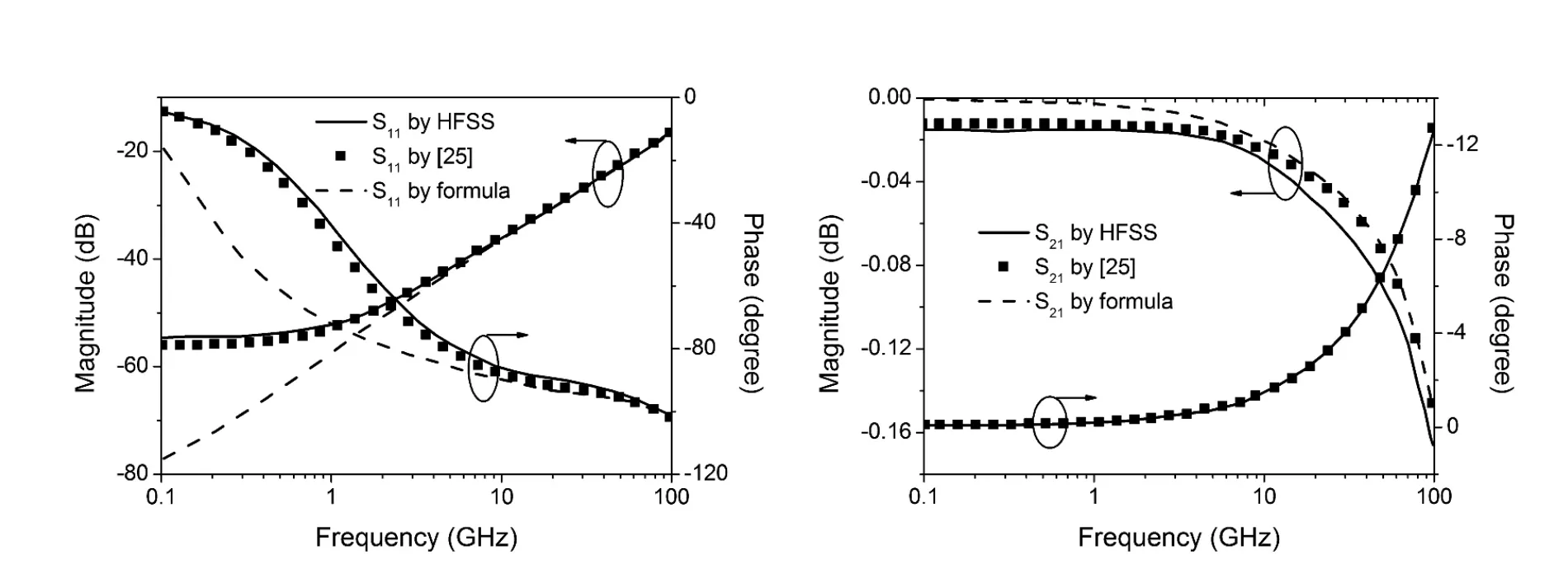
图4 同轴硅通孔的散射参数[25]
进一步地,针对三维集成电路中的互连应用,还需发展精度可靠的硅通孔网络建模技术。此外,由于在对三维集成电路各种关键器件进行系统优化时通常需要不断调整和修改器件的物理结构或几何尺寸参数,必须寻求一种更为准确高效的建模和优化技术,例如利用人工神经元网络方法[26-31]可以建立参数化的硅通孔网络模型。
利用提取的寄生参数建立三维集成电路互连线等效电路模型,通过电路仿真工具SPICE可以进行信号完整性分析。信号完整性分析包括时域响应分析和频域分析,通过观察信号时域响应可以获得互连线信号时延、串扰、下冲、过冲、误码率等信息;频域分析主要是观察电路的回路损耗和插入损耗随频率的变化。
4 结束语
三维集成电路利用硅通孔(TSV)技术,将多个有源层在垂直方向堆叠起来,从而极大地提升了芯片的集成密度。同时,信号通过TSV在垂直方向上传输,使不同分层器件实现最小路径互连,从而减小时延和功耗,提高了系统性能。然而,三维集成电路也面临着诸多技术难题,如散热问题、设计自动化问题。本文简要评述了三维集成电路设计自动化算法,指出三维模块数据结构和热驱动的物理设计是三维集成电路设计自动化算法的关键部分。最后,本文详细介绍了TSV技术,给出了TSV的电路建模方法,并对其发展趋势给予了展望。
[1]Topol A W,Tulipe D C La,Shi L,et al.Three-dimensional integrated circuits[J].IBM Journal of Research and Development,2006,50(4.5):491 -506.
[2]Motoyoshi M.Through-silicon via(TSV)[J].Proceedings of IEEE,2009,97(1):43 -48.
[3]Li J F,Wu C W.Is 3D integration an opportunity or just a hype?[C].Taipei:15th Asia and South Pacific Design Automation Conference.2010:541 -543.
[4]Hsu M K,Balabanov V,Chang Y W.TSV-aware analytical placement for 3-D designs based on a novel weighted-average wirelength model[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2013,32(4):497-509.
[5]Kleiner M B,Kuhn S A,Ramm P,et al.Thermal analysis of vertically integrated circuits[C].Washington:IEEE International Electron Devices Meeting.1995:487 -490.
[6]Wilkerson P,Furmanczyk M,Turowski M.Compact thermal model analysis for 3-D integrated circuits[C].Szczecin:International Conference on Mixed Design of Integrated Circuits and Systems.2004:277 -282.
[7]Digele G,Lindenkreuz S,Kasper E.Fully coupled dynamic electro-thermal simulation[J].IEEE Transactions on Very Large Scale Integration(VLSI)Systems,1997,5(3):250 -257.
[8]Wunsche S,Claub C,Schwarz P,et al.Electro-thermal circuit simulation using simulator coupling[J].IEEE Transactions on Very Large Scale Integration(VLSI)Systems,1997,5(3):277 -282.
[9]Shockley W.Semiconductive wafer and method for making the same[P].US Patent:US3236698,1994-04-08.
[10]Katti G,Stucchi M,Meyer K De,et al.Electrical modeling and characterization of through silicon via for threedimensional ICs[J].IEEE Transactions on Electron Devices,2010,57(1):256 -262.
[11]Chen Q,Huang C,Wu D,et al.Ultralow-capacitance through-silicon vias with annular air-gap insulation layers[J].IEEE Transactions on Electron Devices,2013,60(4):1 421 -1 426.
[12]Wang G,Pan G W.Full wave analysis of microstrip floating line structures by wavelet expansion method[J].IEEE Transactions on Microwave Theory and Techniques,1995,43(1):131 -142.
[13]Wang G,Qi X,Yu Z,et al.Device level modeling of metal-insulator-semiconductor interconnects[J].IEEE Transactions on Electron Devices,2001,48(8):1 672 -1 682.
[14]Liang F,Wang G,Ding W.Low numerical dispersion locally one-dimensional FDTD method based on compact higherorder scheme[J].Microwave and Optical Technology Letters,2008,50(11):2 783 -2 787.
[15]Ndip I,Curran B,Lobbicke K,et al.High-frequency modeling of TSVs for 3-D chip integration and silicon interposers considering skin-effect,dielectric quasi-TEM and slow-wave modes[J].IEEE Transactions on Components,Packaging,and Manufacturing Technology,2011,1(10):1 627 -1 640.
[16]Pan G W,Wang G,Gilbert B K.Edge effect enforced boundary element analysis of multilayered transmission lines[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Application,1992,39(11):955 -963.
[17]Zhao W S,Yin W Y,Wang X P,et al.Frequency-and temperature-dependent modeling of coaxial through-silicon vias for 3-D ICs[J].IEEE Transactions on Electron Devices,2011,58(10):3 358 - 3 368.
[18]Savidis I,Friedman E G.Closed-form expressions of 3-D via resistance,inductance,and capacitance[J].IEEE Transactions on Electron Devices,2009,56(9):1 873 -1 881.
[19]Zhao W S,Wang X P,Yin W Y.Electrothermal effects in high density through silicon via(TSV)arrays[J].Progress In Electromagnetics Research,2011,115:223 -242.
[20]Xu C,Li H,Suaya R,et al.Compact AC modeling and performance analysis of through-silicon vias in 3-D ICs[J].IEEE Transactions on Electron Devices,2010,57(12):3 405 -3 417.
[21]Liu E X,Li E P,Ewe W B,et al.Compact wideband equivalent-circuit model for electrical modeling of through-silicon via[J].IEEE Transactions on Microwave Theory and Techniques,2011,59(6):1 454 -1 460.
[22]Liang Y,Li Y.Closed-form expressions for the resistance and the inductance of different profiles of through-silicon vias[J].IEEE Electron Device Letters,2011,32(3):393 -395.
[23]Cheng T Y,Wang C D,Chiou Y P,et al.A new model for through-silicon vias on 3-D IC using conformal mapping method[J].IEEE Microwave and Wireless Component Letters,2012,22(6):303 -305.
[24]Xu C,Suaya R,Banerjee K.Compact modeling and analysis of through-Si-via induced electrical noise coupling in 3-D ICs[J].IEEE Transactions on Electron Devices,2011,58(11):4 024 - 4 034.
[25]Liang F,Wang G,Zhao D,et al.A wideband impedance model for coaxial through-silicon vias in 3-D integration[J].IEEE Transactions on Electron Devices,2013,60(8):2 498 -2 504.
[26]Liu X,Wang G,Deng D,et al.A new model of on-chip inductors on ferrite film using KB-FDSMN neural network[J].International Journal of RF and Microwave Computer-Aided Engineering,2010,20(4):399 -407.
[27]Cao Y,Wang G,Zhang Q J.A new training approach for parametric modeling of microwave passive components using combined neural networks and transfer functions[J].IEEE Transactions on Microwave Theory and Techniques,2009,57(11):2 727-2 742.
[28]Rayas-Sanchez J E.EM-based optimization of microwave circuits using artificial neural networks:The state of the air[J].IEEE Transactions on Microwave Theory and Techniques,2004,52(1):420 -435.
[29]Cao Y,Wang G.Efficient modeling of RF CMOS spiral inductors using generalized knowledge-based neural network[J].Analog Integrated Circuits and Signal Processing,2007,52(3):71 -77.
[30]Liu X,Wang G,Liu J.A wideband model of on-chip CMOS interconnects using space-mapping technique[J].International Journal of RF and Microwave Computer-Aided Engineering,2011,21(4):439 -445.
[31]Burrascano P,Mongiardo M.A review of artificial neural networks applications in microwave CAD[J].International Journal of RF and Microwave Computer-Aided Engineering,1999,9(3):158 -174.
