在Matlab中实现熵权TOPSIS法对地下水综合评价

黄耀裔，魏 星，苏建云，杨琳珩，陈文成

（泉州师范学院 资源与环境科学学院，泉州 362000）

在Matlab中实现熵权TOPSIS法对地下水综合评价

黄耀裔，魏 星，苏建云，杨琳珩，陈文成

（泉州师范学院 资源与环境科学学院，泉州 362000）

在Matlab中编程实现基于熵权的TOPSIS法综合评价模型。利用此模型对福建省晋江市浅层地下水环境质量进行综合评价，引入《地下水质量标准》中的五类标准值作为虚拟水样监测点来划分水质评价等级，并对水质质量进行优劣排序，评价等级结果与基于因子分析法评价结果基本一致，表明该法具有一定的可行性，且计算简便，代码易于移植复用，也可用于其他方面评价。

信息熵；TOPSIS法；浅层地下水；综合评价

水资源既是重要的自然资源之一，同时是重要的自然环境因素，是环境可持续发展问题的核心。张新钰等（2011）在地下水污染研究进展中阐述到地下水作为水资源的重要组成部分，在保障我国城乡居民生活用水、支撑社会经济发展和维持生态平衡等具有重要的作用。地下水环境质量评价时受诸多因素的影响，是一个典型的多指标决策问题，王晓鸥（2014）的相关研究指出评价时如果采用单一指标评价常会丢失部分信息,难以解释内在的复杂关系，甚至会得到与事实不符的结论。对此许多研究人员试图采用不同方法克服上述问题的方法，如苏建云和黄耀裔（2014）采用模糊综合评判法、赵焱等（2012）采用灰色聚类关联法、汪晓静和陈锁忠（2008）采用属性识别模型法、周清锋和蒋波（2012）采用物元可拓分析法、周惠成和董四辉（2005）采用投影寻踪法等，每种评价方法都各具优点和不足。对此论文为了尽量克服人为主观赋权的缺陷，采用熵权确定指标权重；再利用Hwang C L和Yoon K于1981年提出的TOPSIS法计算贴近度，最后据标准确定综合评价等级，该法可以在一定程度上克服对样本数量和数据分布的限制，同时采用Matlab矩阵软件对该法进行程序设计，减少了计算量，代码易于移植复用，可用于其他方面的决策评价。

晋江市（24°30′～24°54′N，118°24′～118°43′E），位于福建省东南沿海，地势呈现出北西高—南东低，由西北向东南缓倾，地貌以台地、平原为主；境内地质属于闽东滨海加里东隆起带，断裂发育明显，呈现出密集带状分布，为晋江市地下水的赋存提供了良好的地质环境；气候属南亚热带湿润气候区，每年存在有不同程度的干旱季节导致浅层地下水资源分布不均，水质受影响。

根据国土资源部开展的地下水资源调查，晋江市目前水资源较贫乏，多年平均水资源总量（包括地表水、地下水）为4.1×109立方米，只能依靠客水来拟补各类用水需要。由于近几年充分发挥其地理区位优势，工业、加工业等发展较迅速，导致部分企业废水未经处理随意乱排，与此同时农业引污灌溉、排污管道等向下渗透。本研究在境内地下水水质监测结果的基础上对其综合评价，目的是了解目前晋江市浅层地下水质量状况，为提升晋江市水资源可持续利用能力，促进人口、资源、环境和经济的协调发展，确保晋江市的可持续发展提供参考。

1 熵权TOPSIS法

1.1 熵权TOPSIS法原理

TOPSIS法（Technique for order preference by similarity to ideal solution）主要根据有限个评价对象和逼近于理想解进行排序的一种方法，常用于效益评价、决策、管理等领域的多目标决策。参照顾雪松（2009），朱珠等（2012）的研究，将该法应用于对浅层地下水的综合评价，其基本流程：首先对浅层地下水水质检测数据作归一化处理，找出评价等级中的最优和最劣评价等级（即最优和最劣向量），再结合熵权分别计算评价对象的最优和最劣评价等级的相对距离，获得各评价对象与最优评价等级的相对贴近度以此作为评价结果优劣依据。

1.2 熵权TOPSIS法计算步骤

1.2.1 建立浅层地下水初始评价矩阵

根据浅层地下水评价对象和评价指标建立浅层地下水水质监测点初始评价矩阵X = (xij)m×n（i = 1，2，…，n；j = 1，2，…，m）。其中xij表示为第m个浅层地下水评价单元的第n个评价监测值，初始指标集矩阵表示为：

1.2.2 建立浅层地下水标准化决策矩阵

多指标评价过程不同量纲的指标会给评价带来一定困难，对原始指标做归一化处理可有效克服，由于浅层地下水评价属于越小越优型指标，因此对归一化做修正，其越小越优的指标：

根据修正的归一化后数据建立标准化决策矩阵Z=(zij)m×n。zmn表示经趋势化处理后的第m个评价单元的第n个评价指标值。决策矩阵表示为：

1.2.3 根据信息熵确定权重

权重的确定通常有主观赋权和客观赋权两种，通常采用专家打分法等主观赋权，虽然能较好地反映专家经验，但把握程度有时过于主观性，难免客观事实度不高。论文评价权重选用Shannon熵，参见卞建民等（2007）研究，该权重主要是从指标包含有多少被评价对象分辨信息多少来确定指标重要性，确定原则是当某项指标被评价指标间数值的离差越大则信息含量越多，反之则越少。其权重计算步骤为：

1）构建评价指标判断矩阵R：

2）对判断矩阵bij做归一化处理：

式（5）中，xmax、xmin分别为浅层地下水同一指标下不同方案中最满意者或最不满意者（越小越满意或越大越满意）。

3）根据熵定义确定评价指标的熵：

4）计算评价指标的熵权W：

1.2.4 构造规范化加权决策矩阵

将无量纲化的指标和权重按照式（9）计算后得到加权后的决策矩阵（10）。

通过规范化决策矩阵确定正理想解向量C+和负理想解向量C–：

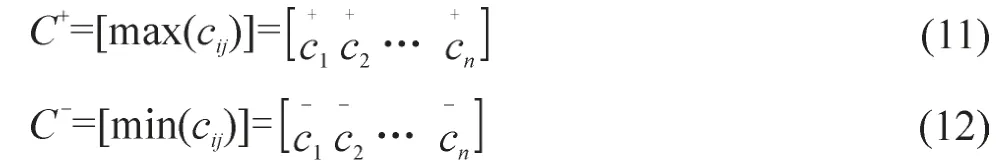
评价对象与最优评价等级及最劣评价等级的距离分别为：

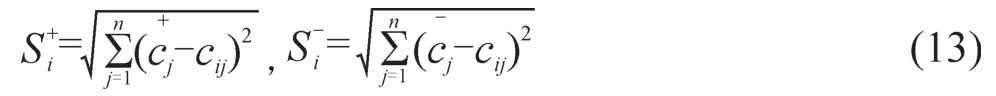
最后计算各评价对象对于理想解的贴近度：

其中0≤Di+≤100%，贴近度的大小反映出各目标解与理想解之间的贴近程度。其中Di+介于0～100%，当评价对象越靠近正理想解，Di+越接近100%，说明评价水平越优；反之则越差。

2 基于Matlab实现TOPSIS解算

Matlab矩阵软件是美国MathWorks公司出品的商业数学软件，可以快速地实现矩阵运算、绘制函数和数据、算法编程、连接其他编程语言等。借助该软件编程基于熵权的TOPSIS法，避免了繁琐的计算，以下是实现过程中部分关键代码。

3 实例分析

以能够基本了解和客观反映目标区浅层地下水水质特征为原则布点，水质监测点采集分布见图1。

根据《地下水质量标准》（GB/T14848-93）选取总硬度、TDS、氯化物、硝酸盐、亚硝酸盐、氟化物、汞、氨氮等共计15个评价指标构建综合评价矩阵（见表1）。首先据Shannon熵确定评价指标的权重分别为（0.08，0.07，0.08，0.05，0.06，0.08，0.07，0.06，0.04，0.05，0.06，0.06，0.09，0.06，0.08），将以标准中的5个评价等级限制作为5个虚拟地下水水样监测点数据，结合60组待评价水样点数据共65组数据基于熵权TOPSIS法，通过Matlab编程计算实现其贴近度大小。计算结果得出5个虚拟地下水水样监测点数据（即依据地下水质量标准中的Ⅰ～Ⅴ类水质标准）的贴近度值：0.84、0.73、0.51、0.19，因此可依次划分Di+＞0.84为Ⅰ类水质；Di+介于0.84～0.73为Ⅱ类水质；Di+介于0.73～0.51为类Ⅲ水质；Di+介于0.51～0.19为Ⅳ类水质，Di+＜0.19为Ⅴ类水质，以此结果作为划分评价等级的基准，以此区分出所有待评价监测样点的评价等级。待评价水样点分级结果和利用贴近度对评价结果进行综合排序结果见表2。

基于熵权的TOPSIS法的评价结果与采用因子分析评价的结果总体保持一致（其中有9个评价样本存在差异），从各个地下水浅层水质监测点的实际情况看，排名靠后的几个监测点主要位于工业区、农业种植区或者临海区域，说明工业污水排放、农业生产或者海水入侵等影响导致水质变差。

图1 晋江市浅层地下水水样监测点Fig.1 Shallow groundwater monitoring points in Jinjiang city

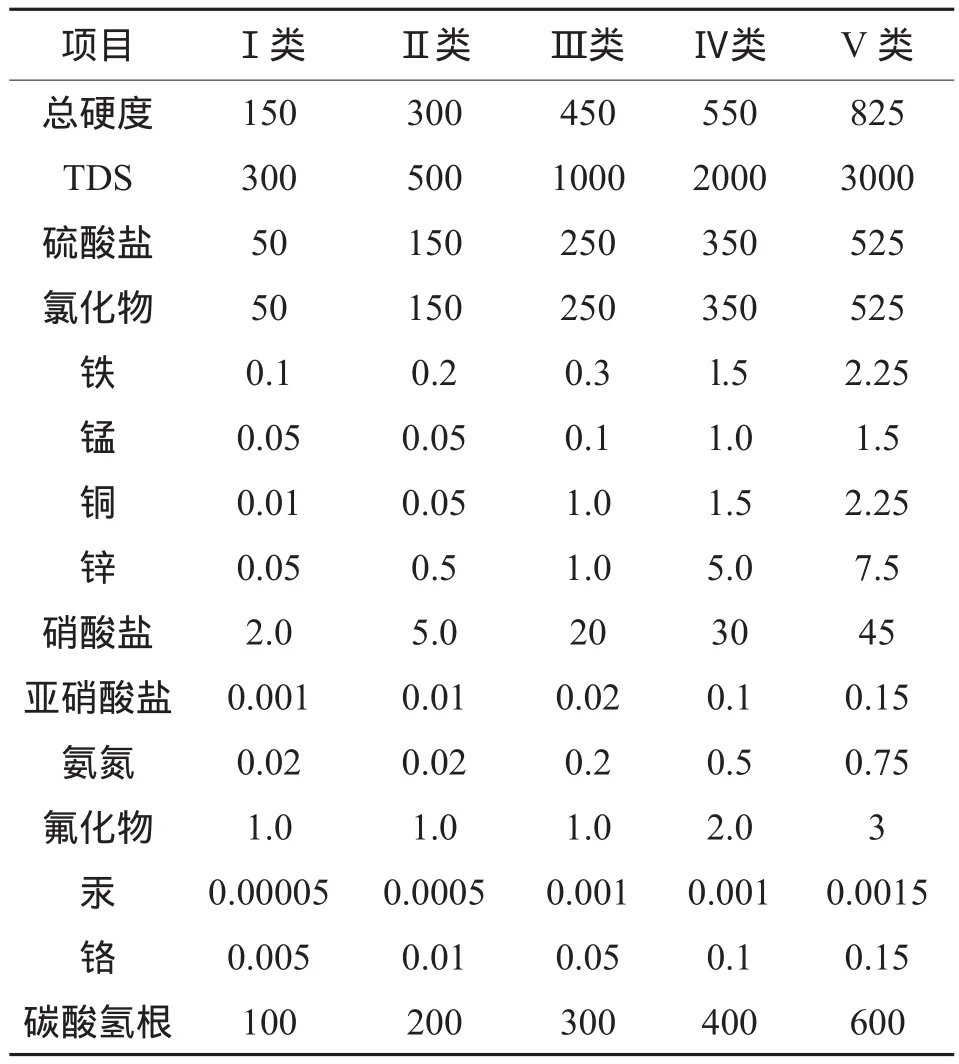
表1 地下水单项指标质量分类Table 1 Quality classif cation of groundwater targets (mg·L−1)

4 结语

引入信息熵理论进行客观赋权，在一定程度上避免了权重计算的主观性，提高了传统TOPSIS法的科学性和合理性。利用Matlab编程计算基于熵权的TOPSIS法，计算量小，方便快速，易于掌握。还可应用于项目决策评价等，为多目标决策提供了一条新途径，具有广阔的应用前景。

表2 晋江市浅层地下水质量评价结果Table 2 Evaluation results of groundwater quality in Jinjiang

（续表2）

由以上结果可得知，利用基于熵权的TOPSIS模型评价地下水，其评价结果与基于因子分析的评价结果基本一致，说明该评价方法可行。通过虚拟的标准样点的贴近度对待评价样点分级，同时在同一水质类别中还可以细化水质优劣的评价，给出更直观的判断，对贴近度的大小进行排序，相对贴近度越大表明越接近最优方案，有利于水质评价工作的进行。同时该法可应用到其他方面的决策评价。

卞建民, 汤 洁, 李立军. 2007. 辽河油田地区地下水水质的熵权属性识别评价[J].水文, 27(3): 46 – 49. [Bian J M, Tang J, Li L J. 2007. Application of attribute recognition model based on coefficient of entropy in groundwater quality assessment for the Liao he oil f eld area [J]. Journal of China Hydrology, 27(3): 46 – 49.]

顾雪松. 2009.基于熵权TOPSIS 的上市公司财务评价模型及石化行业的实证[J].价值工程, (8): 159–164. [Gu X S. 2009. The f nancial evaluation model of listed companies based on entropy-weight TOPSIS and empirical studying on petrochemical industry [J]. Value Engineering, (8): 159–164.]

苏建云, 黄耀裔. 2014.修正的模糊数学综合评判法在地下水环境质量评价中的应用——以福建省晋江市为例 [J].西南师范大学学报(自然科学版), 39(7): 78–85. [Su J Y, Huang Y Y. 2014. Application of modif ed fuzzy comprehensive mathematics evaluation method in the comprehensive assessment of groundwater environment quality—Taking Fujian province Jinjiang city as an example [J]. Journal of Southwest China Normal University (Natural Science Edition), 39(7): 78–85.]

汪晓静, 陈锁忠.2008.基于熵权的属性识别模型在地下水源地水质评价中的应用[J].煤田地质与勘探，36(3): 56–58. [Wang X J, Chen S Z. 2008. Application of attribute recognition model based on coeff cient of entropy to evaluation of groundwater sources quality [J]. Coal Geology＆Exploration, 36(3): 56–58.]

王晓鸥. 2014.基于改进内梅罗污染指数法和模糊数学的水质评价[J].西部探矿工程, (5): 103–107. [Wang X O. 2014. Evaluation of water quality based on improved nemerow index method and fuzzy mathematics [J]. West-China Exploration Engineering, (5): 103–107.]

张新钰, 辛宝东, 王晓红, 等. 2011.我国地下水污染研究进展[J]. 地球与环境, 39(3): 415– 422. [Zang X J, Xin B D, Wang X H, et al. 2011. Progress in research on groundwater pollution in our country [J]. Earth and Environment, 39(3): 415– 422.]

赵 焱, 王 婷, 徐 曦. 2012.改进灰色聚类关联在地下水水质评价中的应用[J]. 人民黄河, 34(7): 346–352. [Zhao Y, Wang T, Xu X. 2012. Application of improved grey clustering relation model in groundwater quality assessment [J]. Yellow River, 34(7): 346–352.]

周惠成, 董四辉. 2005.基于投影寻踪的水质评价模型[J].

水文, 25(4): 14–17. [Zhou H C, Dong S H. 2005. A water quality assessment model based on projection pursuit technique [J]. Journal of China Hydrology, 25(4): 14–17.]

周清锋, 蒋 波. 2012.物元分析方法在苏州浅层地下水质量评价中的应用[J].地质学刊, 36(1): 80–85. [Zhou Q F, Jiang B. 2012. Application of element unit analysis in evaluation of shallow groundwater quality in Suzhou city [J]. Journal of Geology, 36(1): 80–85.]

朱 珠, 张 琳, 叶晓雯, 等. 2012.基于TOPSIS方法的土地利用综合效益评价[J]. 经济地理, 32(10): 139–144. [Zhu Z, Zhang L, Ye X W, et al. 2012. Evaluation of comprehensive land use eff ciency based on TOPSIS [J]. Economic Geography, 32(10): 139–144.]

Application of entropy weighted TOPSIS method in groundwater comprehensive evaluation implemented in Matlab

HUANG Yao-yi, WEI Xing, SU Jian-yun, YANG Lin-heng, CHEN Wen-cheng
(School of Resources and Environmental Science, Quanzhou Normal University, Quanzhou 362000, China)

Entropy-weight TOPSIS method was implemented in Matlab software. The environmental quality of shallow groundwater in Jinjiang city, Fujian province was evaluated by this method. The f ve standard values in quality standard for groundwater were used to divide the grade of water quality as virtual water monitoring points. And then the water environmental quality was ranked in this paper. Compared with the factor analysis method, the evaluation results on the two approaches were basically the same. The results showed that entropy weighted TOPSIS method had certain feasibility and the calculation was simple. What’s more, the programme codes were easy to be transplanted. And this method can be used for other aspects of evaluation.

information entropy; TOPSIS method; shallow groundwater; comprehensive evaluation

10.7515/JEE201404004

X824

A

1674-9901(2014)04-0261-05

2014-06-29

福建省创新实验项目（201410399032）；泉州市科技局项目（2012Z117）

黄耀裔，E-mail: huangyaoyi@163.com