基于改进的SIFT算法的异源影像匹配
2014-09-29蒋丹妮周天顺
宛 蓉,蒋丹妮,周天顺
(1. 61363部队,陕西 西安 710054)
随着影像获取方式日益多样,如何对异源遥感影像进行匹配,是摄遥感影像处理中较为棘手和重要的问题。与传统影像不同,异源遥感影像之间存在灰度信息、比例尺差别大,甚至还存在较大旋转的情况。Dajimdi等提出基于小波变换的不同分辨率影像之间的匹配[1]。张祖勋等提出一种基于多级影像概率松弛整体匹配的方法,可用于不同时相、不同分辨率的遥感影像匹配[2]。近年来,出现于计算机视觉中的SIFT匹配算法得到广泛应用。SIFT匹配算法不仅对图像缩放、平移和旋转变换具有不变性,而且对光照变换以及复杂的仿射和投影变换也具有部分不变性[3],匹配可靠性很高。本文将其引入异源遥感影像匹配之中,并对误匹配点的删除进行研究。实验表明,采用此算法能得到较好的匹配结果,为异源影像之间的高精度快速匹配提供了一种思路。
1 SIFT匹配算法原理简介
1.1 尺度空间生成
尺度空间描述的是影像数据的多尺度特征,其构成方式为影像与高斯核函数的卷积。因此二维图像的尺度空间可定义为[4]:
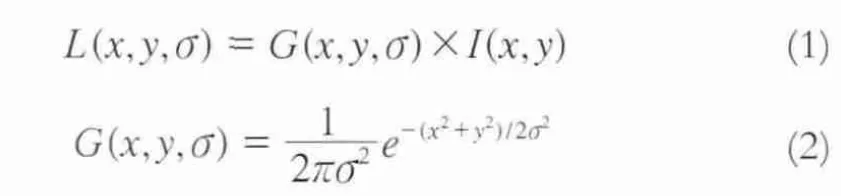
式中,G(x,y,σ)是尺度高斯函数;(x, y)描述的是影像坐标;σ为尺度因子。
为了有效地在尺度空间检测到稳定的关键点,Lowe提出高斯差分尺度空间(DOG scale space),利用不同尺度的高斯差分核与图像卷积生成:

1.2 尺度空间极值检测
尺度空间极值检测的主要目的是初步确定关键点所在位置和尺度。每一个采样点与其相邻点作比较,初步确定影像上的极值点。为了确保其在尺度空间和影像上都检测到极值点,一般还需和上下相邻尺度对应的点作比较,如图1所示[5]。
1.3 特征点定位
特征点定位的目的是去除极值点中对噪声敏感的点或非边缘点。主要方法是在极值点处用泰勒二次级数展开,并进行对比度检测,删除对比度低的极值点。同时,利用Hessian矩阵的迹和行列式的比值减少DOG函数的边缘效应。
1.4 关键点方向分配
关键点方向分配是基于图像局部特性描述特征点的方位信息,使算子对图像具备旋转不变性。
1.5 提取特征描述符
由于每个特征点都包含有位置、尺度和方向信息,因此在匹配时特征点对几何变换具有不变性。对每一个特征点构建特征描述符,使其对亮度和视角变化保持不变[6]。其步骤为:首先将坐标轴进行旋转,使其为关键点方向,以确保旋转不变性。然后以特征点为中心取像素窗口(一般为16像素×16像素),并分成l6个子区域,在每个子区域上以45°为步长计算0~315°共8个方向的梯度大小和梯度方向直方图,从而每个子区域可得到具有8个方向的描述符,每个特征点可得到128个方向的描述符,即形成128维的特征描述符向量。最后将特征描述符向量进行归一化处理,并对梯度幅值设置阈值,使其对亮度变化和照度不均的情况不敏感。
1.6 特征点匹配
利用特征描述符向量的欧氏距离作为特征点的匹配测度,欧氏距离最小的两个特征点可以认为是匹配的候选点对。然后用最小的欧氏距离除以第二小的欧氏距离,若其比值小于某个阈值,则可将其当成匹配点。阈值设置越小,则匹配条件越苛刻,相应地得到的匹配点数就越少,但匹配结果就越可靠。
2 SIFT算法改进
2.1 传统匹配策略缺点
传统特征点匹配方法采用最小欧氏距离与第二小欧氏距离的比值来判断是否为匹配点。若比值小于阈值,则为正确匹配点,否则舍弃。设定的阈值越小,匹配准确率越高,但同时也排除了部分正确匹配点。此外,该方法没有考虑重复匹配及其他误匹配点情况,因此需对匹配精度进一步优化。
2.2 误匹配点删除
误匹配点的删除使用随机抽样一致算法(RANSAC)。RANSAC是一种迭代的粗差剔除方法,用来在一组包含粗差的被观测数据中估算出数学模型的参数,通过几何一致性检验剔除少数精度较低的匹配点[7]。RANSAC方法将数据分为Inliers和Outliers,通过反复选择数据中的一组随机子集来达成目标。具体步骤为:
1)从匹配结果中随机取出一些匹配点对,计算变换参数,作为初始的平移矩阵模型。
2)根据得到的初始模型遍历匹配结果中的所有匹配对,若匹配对在预定阈值下适用于该初始模型,则记为Inliers。计算Inliers占匹配对的百分比,若大于选定阈值,对剩余的匹配点对作最小二乘估计,计算Inliers与估计模型的错误率。
3)重复前两步骤,取对应错误率最小的变换参数作为最终的最佳模型。
4)将在最佳模型下误差超过预定阈值的匹配对(Outliers)去除。
5)对去除后的匹配点对重复上述步骤。
3 实验分析
实验数据包括两组:一组为中巴地球资源2号卫星(CBERS02)航天影像和SWDC数字航空摄影仪的航空影像,如图2;另一组为SPOT 5 的2.5 m全色影像和10 m多光谱影像,如图3。两组影像之间在灰度、分辨率等方面存在较大差异,拍摄时间的不同甚至可能导致影像上地物的变化。


对于这种不同源的遥感影像,本文首先采用最小欧氏距离与第二小欧氏距离比值法进行SIFT初始匹配(本文阈值为0.35),然后利用RANSAC算法(本文阈值为0.6)剔除明显的误匹配点,最终得到匹配点对15个。从图4可知,匹配结果基本上都是正确的,并且匹配点基本能分布于整幅影像。

同样,采用SIFT匹配算法对SPOT 5多光谱影像和全色影像进行匹配,剔除明显的误匹配点后共得到26个匹配点。从图5可知,匹配点主要集中于城区,纹理缺乏的山区匹配点相对较少。

4 结 语
为解决不同源影像之间难以匹配的问题,引入计算机视觉中已广泛应用的SIFT匹配算法,并对误匹配点的删除进行研究。结果显示,相对于传统匹配算法,利用SIFT算法可以对异源遥感影像进行高精度的匹配。在下一步的研究中,应主要集中于如何提高纹理缺乏区域的匹配点个数,从而使匹配点分布更加均匀。
[1]Djamdji J.Geometrical Registration of Images:the Multiresolution Approach[J]. Photogrammetry and Remote Sensing,1993, 59(5):645
[2]张祖勋,张剑清,廖明生.遥感影像的高精度自动配准[J].武汉测绘科技大学学报,1998,23(4):320
[3]李芳芳,肖本林,贾永红,等. SIFT算法优化及其用于遥感影像自动配置[J].武汉大学学报:信息科学版,2009,34(10):1 245-1 249
[5]张继贤,李国胜,曾钰.多源遥感影像高精度自动配准的方法研究[J].遥感学报,2005,9(1):73-77
[6]Lowe D G.Distinctive Image Features from Scale-invariant and keypoints[J].International Journal of Computer Vision,2004,60(2):91-110
[7]刘小军,杨杰,孙坚伟,等.基于SIFT的图像配准方法[J].红外与激光工程,2008,37(4):156-160
[8]Fischler M A,Bolles R C. Random Sample Consensus:A Paradgm for Model Fitting with Applications to Image Automated Cartography[J]. Communication of the ACM,1981,24(6):381-395
