一种流数据立方体分析挖掘框架*
2014-09-29金苍宏刘泽民吴明晖
金苍宏 ,刘泽民 ,吴明晖 ,应 晶 ,
(1.浙江大学计算机科学与技术学院 杭州 310027;2.浙江大学城市学院 杭州 310015)
1 引言
联机分析挖掘(online analytical mining,OLAM)是一种结合数据挖掘和联机分析处理 (online analytical processing,OLAP)的知识发现方法。使用OLAM可在多维数据库的不同数据子集和抽象层次上进行探索式挖掘,因此在决策定制、市场分析、可视化等领域都发挥着重要作用。随着移动互联网的迅速发展和广泛应用,各种类型的数据流规模急剧增大,如金融流数据、图像流数据、社交流数据等。挖掘数据流中包含用户刻面和行为动作的相关信息,成为当前研究的一个热点[1]。如在移动应用分析系统中,通过SDK(软件开发工具包)可以采集应用的名称、使用时间、GPS信息、IP地址、手机型号、网络类型等多个维度的信息。对此类信息进行OLAM分析,可提供灵活的多角度数据分析场景,提高商业竞争能力。例1给出一个流数据OLAM的分析场景。
例1:运营方希望能实时监控某款应用在不同人群中的活跃度,以便其能分析出核心用户,实时调整留存和激活策略,增强其竞争力。
对于不同人群的划分可以使用数据立方体分析,可以在多个子空间中统计相关活跃度。但是,流数据处理具有单次扫描、较低的时间和空间复杂度、适应动态变化的流速等要求,且系统挖掘时效性强,需实时返回分析结果,而事先又无法指定所需要观察的维度组合,需要对维度组合进行全量分析,因此实时计算量巨大。
基于上述的要求,使用现有的OLAM方法,把数据仓库中的记录通过OLAP投射到不同空间生成数据单元,再通过多角度综合分析数据的方法[2]无法满足上述要求,原因如下。
(1)数据量大
和传统的数据仓库相比,移动互联网下的流式数据是海量的且增长迅速。传统OLAP工具在存储空间和计算效率上都无法满足实时性能要求。
(2)数据动态性强
传统OLAP方法,通过对数据立方体建立物化视图(materialized view)可以预计算部分结果,从而提高实时查询的效率,达到空间和效率上的平衡[3],如QC-Tree、侏儒立方体等方法[4]。但流式数据是动态可变的,因此对于数据无法做静态的预处理,必须要实时计算。
(3)数据时效性强
传统OLAP框架处理的是归档数据,对数据的实效性要求不高。而数据流内含的时态特征表明,数据是有生命周期的。用户往往只对特定时间窗口内的数据感兴趣,而忽略窗口外的数据。如例1中,只需要统计分析促销活动过程中的最近的数据,而忽略其他历史归档数据。
由此可见,传统的OLAM方法不能很好地处理数据流。而其他基于数据抽样[5,6]和基于数据压缩[4]两种流式数据处理方法受限于计算能力和存储空间的大小,只在整体空间或几个分组中进行数据分析,如stream[7]、TelegraphCQ[8]、SMM[9]等。但它们没有提供在任意子空间或任意层次中对数据进行分析的方案。
本文提出一种流数据立方体处理框架——sketch cube(概要立方体)。并在storm开源流处理平台中实现。sketch cube在较小的空间中实时聚合有效数据单元信息,可满足OLAM的分析需求,其贡献在于以下几点。
·提出一种可扩展的数据单元标识方法,对流数据的任意维度组合通过配对函数 (pairing function)[10]映射生成唯一标识且保证维度扩展后数据仍不冲突。
·提出一种改进概要统计模型——ACM(advanced count model),ACM根据数据分布特性和存储模型的设计特征,可有效裁剪长尾的数据单元,以提高计算能力和存储空间效率,同时可改进数据单元统计精确度。
·提出一种基于时间窗口的倒排检索模型,可支持任意时间粒度的组合。在类线性存储空间中存放所有有效数据单元的统计信息,最大限度地保证了信息的完整性。
·从理论上给出sketch cube的适用场景和准确率范围。通过storm实现sketch cube功能,且在海量真实数据流下测试模型在不同参数和时间片长度下的吞吐量和准确率。理论分析和实验证明sketch cube的查询效率高且能支持流式数据下的立方体全量分析。
本文研究主要结合传统的OLAP方法和流数据处理方法。
已有的对传统OLAP的扩展研究如(参考文献[11~13])引入了文本属性,提出文本立方体(text cube)概念。Lin C等[13]提出基于关键词的数据立方体查询,对数值和文本维度分别建立层次结构,通过倒排索引检索出相应的数据单元。在此基础上,Ding B等[12]提出基于关键词的top-k数据单元查询问题,通过对关键词的信息检索(information retrieval)度量,提取出与关键词最相关的k个数据单元。与此相反,参考文献[11]提出了数据单元主题判定问题,对给定层次的数据单元结合自然语言模型,判断其所属的主题和相关概率。
流数据结合OLAP操作产生了流立方体(stream cube)的概念。参考文献[4]使用倾斜时间框架(tilted time framework)管理数据,使用线性回归函数对流数据在不同维度上进行压缩。但是该方法物化数据带有主观性,会丢失部分信息。同时在上下层节点合并时需要频繁更新head表,更新速度较慢。文本流数据立方体(如Liu X等[14])通过Twitterstream数据,建立热点图和情感图等应用。该方法虽然使用时间序列分析,但还是把信息看成静态地存放在数据仓库中而进行分析。其他的流数据分析方法,如抽样方法[6,15],通过建立不同的分布概率函数 (probability distribution function,PDF)对异构源数据进行抽样和语义分析,获得不同的权重,通过样本值的上下限来估计实际的聚合值。方法依赖于样本的采集和分布情况,因此对于错误率无法进行有效的控制。参考文献[16]的方法则使用压缩策略,通过对数据特征分析,只保留其主要元素,而过滤其他元素。但它们把数据看成整体,挖掘不同数据流和不同时间段之间的关联关系,而不是有层次的可以进行OLAP操作的模型。
此外,计数型散列技术统计数据的方法有 na觙ve counting bloom filter (NCBF)、d-left counting bloom filter(dlCBF) 和 binary shrinking d-left counting bloom filter(BSdlCBF)等[17]。在此基础上,概要技术[18,19]可在二阶矩阵大小空间内保存流数据,把N个输入元素压缩在lb N的存储空间中。
2 问题描述
2.1 基本概念
定义1 (多维数据流模型 (multi-attribute stream data model,MSDM))定义某时间点上的数据流记录。MSDM为一个二元组结构(S,T),其中,S为多维度数据模型S=(A0,A1,…,Ai:M),Ai表示标准属性,M为度量维度,T为某个时间点。
如 ((Wi-Fi,hz,Samsung∶1),20140510081559) 中 ,S=(Wi-Fi,hz,Samsung∶1) 为 维 度 模 型 ,hz表 示 “杭 州 ”,20140510081559为时间点,1为度量值。
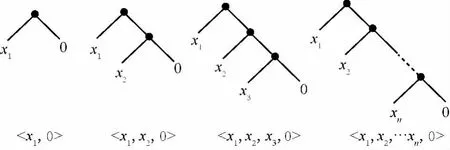
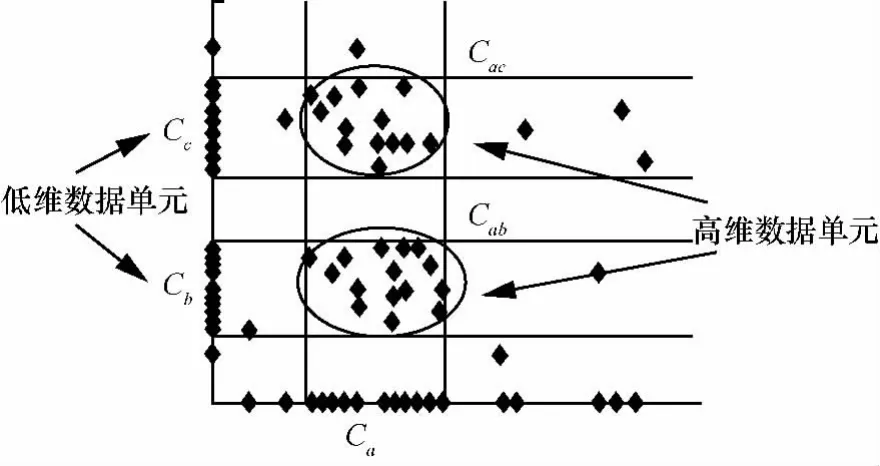
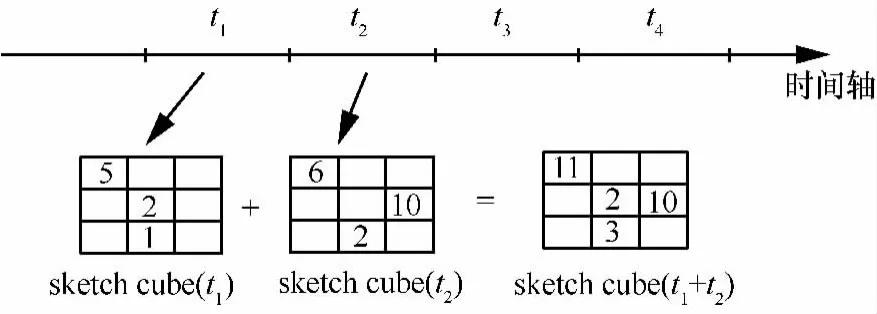
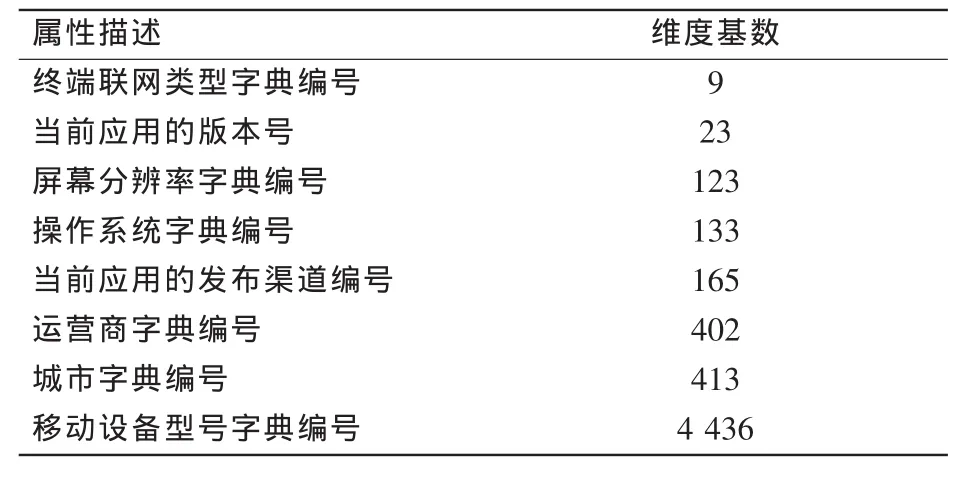
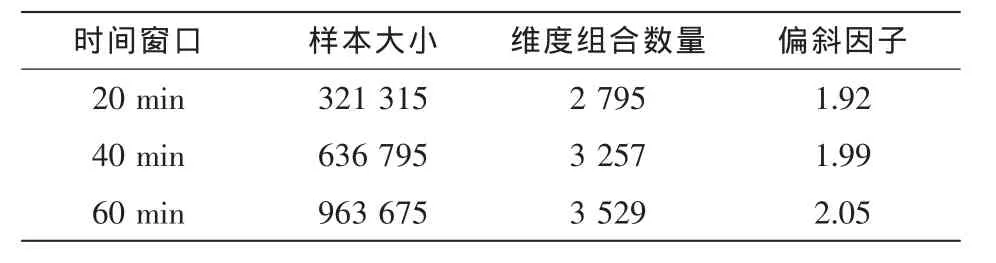
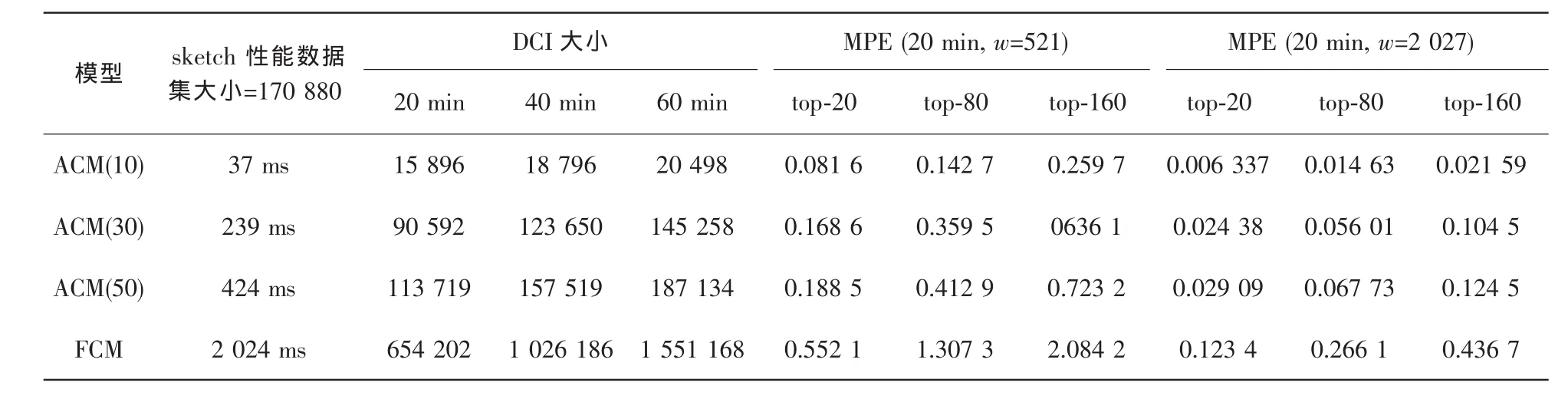
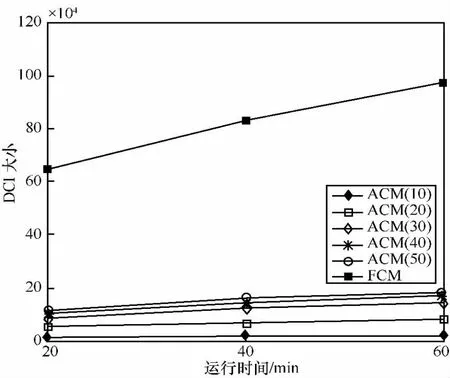
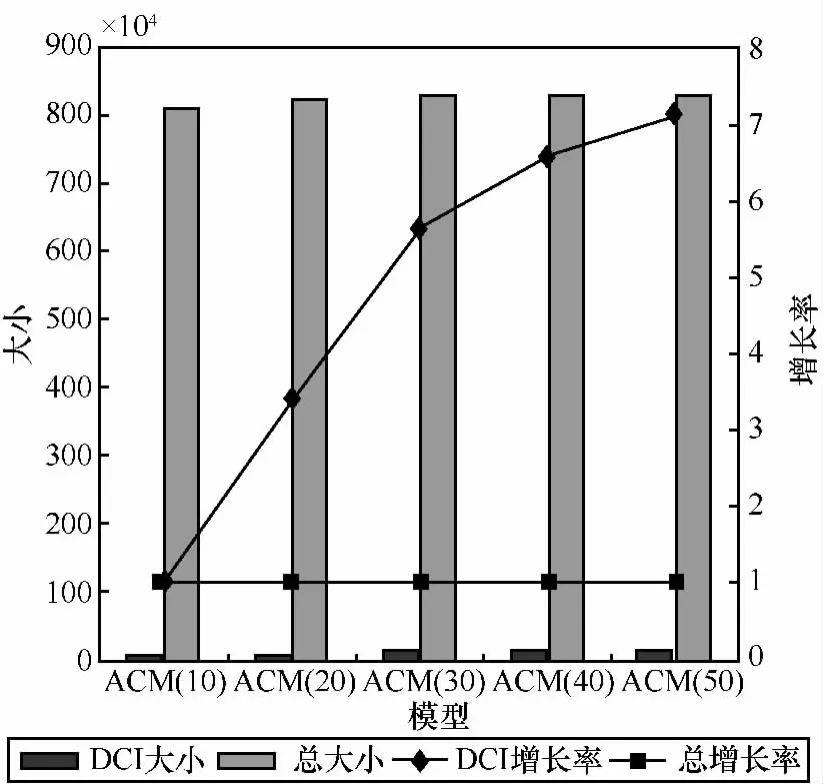
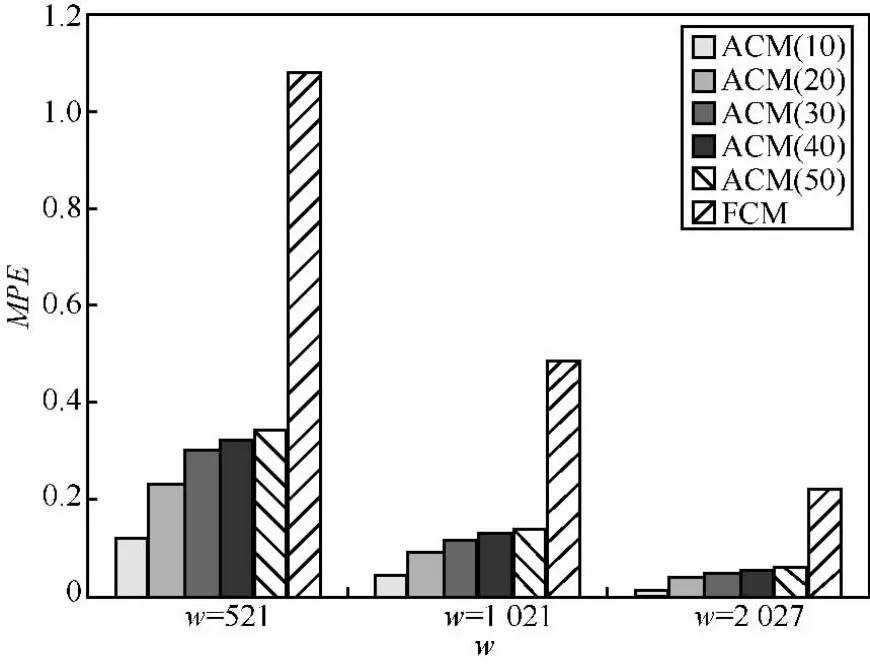
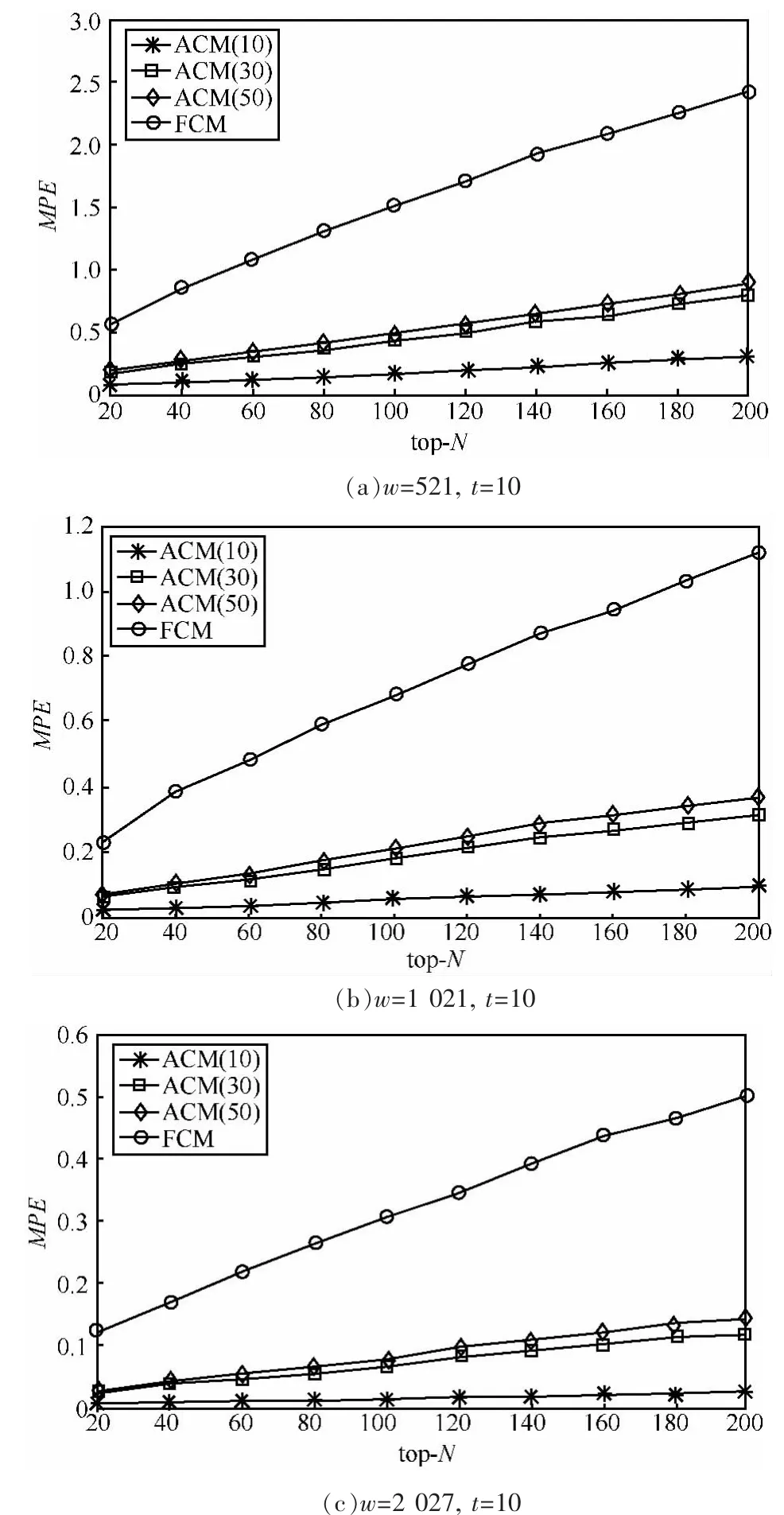
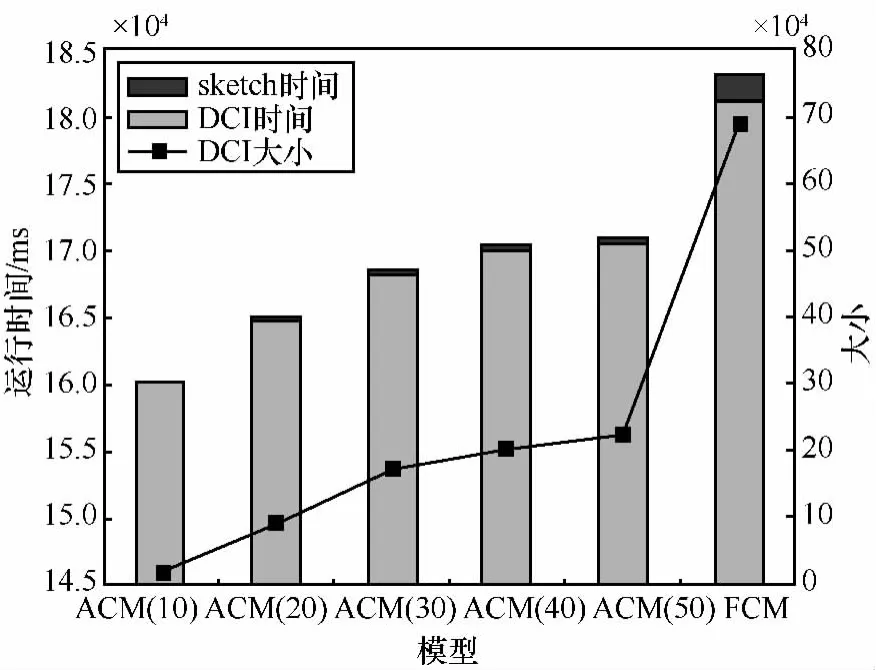
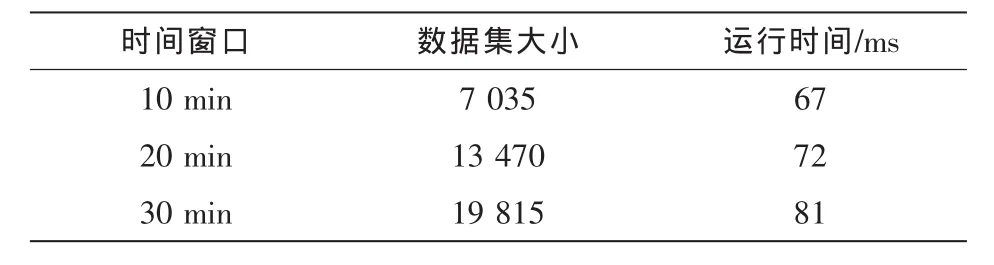
定义2 (流立方体)表示给定一个时间段内的MSDM,按不同的维度构建的一个数据立方体stream cube=(A1,A2,…,An,M,T)。对于stream cube中的每条数据r=(a1,a2,…,an,m,t),其中 r[Ai]=ai∈Ai,ai为属性 Ai的值 ,m 为度量值。对于时间维度T有ti-1 如例1中,给定时间间隔为5 min,在该时间段内收集的所有数据产生的数据立方体,即该时间段内的流立方体。 定义3 (祖先单元和后代单元)对于流立方体中的数据单元Cm和Cn,定义*表示该维度折叠且计算不考虑,则Cm是Cn的祖先(Cn是Cm的后代)可表示为: 记为Cn[t]奂Cm[t],即两个数据单元之间的时间相同,祖先单元至少在一个维度上包含子孙单元且在其他所有维度上和子孙单元的值相等。 对于给定的流数据单元D0=((Wi-Fi,hz,Samsung),20140510081559)的父节点有如下7个: 上述例子中没有显示数据单元的度量值M,祖先单元的度量值可以由其子孙单元的度量值通过聚合操作而计算得出。聚合操作可以分为分布型(distributive)、代数型(algebraic)和整体型(holistic)3 类[20]。 在一组给定的持续的MSDM中,按时间窗口大小,划分出不同的数据片段,按照其维度生成流数据立方体。流数据立方体实时提供了清洁、有组织和汇总的数据,因此可以在不同粒度父子数据单元中分析挖掘。通过和流数据框架的结合,大大增强探索式数据挖掘能力和灵活性。如例1所示,可以满足实时的、全量的多层次数据挖掘的需求。 本节给出构造sketch cube框架所需的主要部件:数据单元标识算法及其改进模型、流数据立方体存储结构和裁剪模型、时间窗口索引等。 流数据立方体产生了海量的维度组合,即数据单元,这些数据单元中的不同属性值包含多种类型,有连续型、离散数值型、字符型等。需要对这些属性值进行字典化处理,并给每个数据单元一个唯一的标识,用于后续计算。 数据单元标识(data cell identifier,DCI)算法的功能就是把不同的维度组合映射成唯一整数,且算法支持维度的扩展,即新增维度或修改维度值都不会与原有映射值冲突。在流数据R=(A1,A2,…,An,M)中,|Ai|表示第i维的基数。使用两个步骤进行数据单元标识。 (1)由于维度值的多样性,需要先把记录R的维度Ai映射成连续的自然数,即: (2)在步骤(1)中产生 n 个自然数 Ni,形成集合 S,使用配对函数对S中的任意非空子集生成唯一的自然数。 配对函数的定义为把两维度元组映射成一维度元组的函数N×N→N。它是一个双射函数,其单调递增的特性如式(3)所示,保证其不会重复。 对于高于两维度的元组可以使用嵌套模式进行,文本使用康托尔配对函数(Cantor tuple function),如图1和式(4)所示,按维度顺序进行嵌套配对,把中间结果当成下一步操作的输入。 图1 有限元素算术图 3.1.1 改进配对函数 康托尔配对函数用嵌套方式生成映射值,当元组维度较高或者某些维度基数较大时,会导致巨大的映射值。提出改进配对函数(advanced pairing function,APF)模型,其思想是在不改变计算模型的同时,产生较小的映射值。其理论依据如下: ·在数据立方体中,维度的顺序与数据单元描述无 关,即数据单元(A1,A2)=(A2,A1); ·在嵌套方法中,越早进入计算的数值参与循环的次数越多,对结果值大小的影响越大。 APF 模型定义如式(5)和式(6)所示。 对给定属性Ai: 如图1所示,嵌套计算从尾部开始,式(5)表示输入配对函数的维度顺序由维度基数大小决定,基数大的维度靠前。式(6)表示把维度值映射成连续自然数时,对出现频率高(freq值大)的维度值赋给小自然数。维度基数的大小和维度值的频率可以由统计或经验获得。如本文实验中,手机操作系统维度基数小于城市维度基数,Android机型多于苹果机型。使用APF模型可以有效地减少大数值在递归中的计算次数,达到最终控制输出映射值的目的。 3.1.2 算法步骤 结合APF模型,给出算法1数据单元标识(DCI)算法的步骤。DCI算法先把流数据中每条记录的维度值映射成由小到大的自然数(行①),通过递归函数得到与之相关的所有维度组合(行②),并使用康托尔配对函数获得所有组合唯一标识(行③~⑦)。 算法1 数据单元标识算法 输入:流数据记录r=(a1,a2,…,ai,m,t) 输出:r所有维度组合标识 ①根据APF模型中式(5)和式(6),将记录r中的维度映射成(n1,n2,…,nn) ②set ③set ④for all x∈{ ⑤ ⑥end for ⑦return 提出一种通过sketch技术对流数据单元进行统计的方法,首先给出模型所需的独立散列族定义。 3.2.1 独立散列族定义 定义4 (均匀散列函数)对于给定的元素集合U通过散列函数h(x)投射到n个元素中,对每个j=1,…,n,给定x∈U,有 P[h(x)=j]=1/n,h(x)则为均匀散列函数。 定义5 (互相独立散列函数族)在F散列族中任意选择a、b两个随机函数,如果且则F为相互独立的散列函数族。 3.2.2 计数最小概要模型 计数最小概要(count-min sketch,CM sketch)模型[10]是一个使用相互独立散列函数族函数统计流数据元素出现频率的模型。其结构如图2所示,是一个d×w的二维数组。 图2 CM sketch存储结构 其中,d表示相互独立散列族函数的个数,w表示每个散列函数的映射范围,如式(7)所示: 显然,n个元素可以表示2n个两两组合元素集合。因此,设计包含d个函数的相互独立散列函数族,只需用个不同元素,如式(8)所示: 从SeedSet中随机取不同的元素a和b,定义散列函数方法如式(9)所示: 由ha,b(z)产生的散列值是变长的,式(10)把值规约到w大小的数组中。 3.2.3 CM sketch效率 对于第t次到达的元素c,计数最小概要模型更新操作如式(11)所示: 即使用不同散列函数找到存储结构中的下标位置,并添加相应值,其更新时间复杂度为 统计元素ai在CM sketch中的估计值a^i的操作如式(12)所示: 即通过散列函数族中的每个函数计算该元素在对应数组中的下标值,获得所有可能值中的最小值即该元素的估计值,其查询时间复杂度为O(1)。 流数据有收款机模型(cash register model)和十字转门模型(turnstile model)两种模型。计数最小概要模型只支持收款机模型,即统计值只能递增,因此基于此的sketch cube只支持分布型聚合操作。对于(A1,A2,…,An)数据立方体,所有数据单元个数则 sketch cube模型的压缩率P为式(13)所示: 3.2.4 模型精度和前提条件 式(14)给出了预测元素ai统计值的偏差范围,即预测统计值a^i小于实际值ai+缀||a||的概率为1-δ,可以根据元素多样性和期望精确度调整缀和δ,进而调整存储模型中的w和d值。 计数最小概要模型是一个数据敏感模型,对于偏斜数据(skew data)的支持较好(Zipfian参数 1 3.2.5 计数平均最小概要模型 对于分布较为均匀的数据集,不同元素之间的冲突影响较大,可使用计数平均最小概要(countmean min sketch,CMM sketch)统计个数。CMM sketch假设元素均匀分布在散列数组中,则对于元素ct的噪音因子定义如式(15)所示: 元素的预测值需要减去噪音因子,元素概要预测值返回结果取各散列数组中的值的中位数,如式(16)所示: 使用上述哪种模型进行统计,由流数据分布特征和业务需求而定。在本文实验中,由于数据单元标识产生的维度组合值是偏斜的,因此采用计数最小概要模型。 由数据单元标识模型产生的维度组合是幂级增长的,如给定n维记录r=(a1,a2,…,an,m,t)可以产生2n种维度的组合。随着维度数量增加,产生的数据单元数量是巨大的。海量的维度组合会导致计数最小概要模型的冲突率变大,影响精确度。因此,需要对维度组合进行裁剪。 在数据立方体不同聚合操作类型中,对分布类型的操作如sum和count,祖先单元(低维数据单元)聚合了其下的所有后代单元(高维数据单元)的值。由此可得后代数据单元的上限(up bound)和下限(low bound),从而可以推理出祖先单元值的范围(up bound-low bound),如式(17)所示: 其中,祖先单元X可以由最小单元Xi集合组成MSP(most specific partition)[13]。对于数据单元X下的任意子空间g的上下限为式(18)所示: 因计数最小概要模型适合于数据浓度大的元素(如大于阈值τ)。如图3所示,结合式(18),数据单元间的包含关系在count操作中体现出单调性,即Cac[count]>τ→Ca[count]>τ,Cc[count]>τ。其他较复杂代数聚合操作如avg的上下限不等式在参考文献[13]中有所定义。 裁剪规则:对于分布型聚合操作,如祖先单元的测量值小于阈值,则所有它的后代单元的测量值必定小于阈值,因此对于计数最小概要模型可以裁剪掉所有后代单元。 由于sketch cube使用计数最小概要模型,针对分布型聚合操作,结合裁剪规则,提出改进统计模型(ACM)。模型通过预测单维数据单元的测量值,达到减少维度组合的目的。如果测量值小于阈值,可以删除所有包含该维度值的子孙单元。如在记录r=(a,b,c)中,若 Ca[count]<τ,则[count]<τ。对于n维度的流数据中,先进行n次单维度统计,假设有k个单维数据单元测量值小于阈值,则可以裁剪的维度为2k,在对于每条流数据中可减少统计操作2k-n次。因为流数据中的维度值往往是稀疏的,因此裁剪模型可以排除大多数的维度组合。如果一维裁剪模型的裁剪效果不佳,可以使用二维或高维裁剪模型,方法类似。算法2结合裁剪方法的维度生成规则。维度裁剪规则如图3所示。 图3 维度裁剪规则 算法2 改进统计模型 输入:流数据记录 r=(a1,a2,…,ai,m,t),τ 输出:r所有维度组合标识。 ①set<1-DCounter>←{}; ②<1-DCounter>←Cak[Count]>τ,1≤k≤i; ③(a1,a2,…,aj)←(a1,a2,…,ai)<1-DCounter>; ④(a1,a2,…,aj)→(n1,n2,…,nj) ⑤set ⑥set ⑦for all x∈{ ⑧ ⑨end for ⑩return 本文使用ACM(m)表示模型取每个维度上频率最高的m个维度值进行组合,可以减少计算模型的复杂度和存储的空间,且能保证最后的高频数据单元不会被裁剪掉。实验给出了使用ACM模型在不同m参数值下的优化效率。 流数据具体有内在时序性,对流数据挖掘用倾斜时间窗口(tilted-time window,TTW)[23]在不同时间粒度(multiple time granularities)上进行分析。如图4所示,sketch cube按时间片段对元素组合进行统计把结果放入计数最小概要模型。sketch cube设计的存储结构可支持任意时间粒度的组合,其合并计算式如式(19)所示: 对于给定散列函数族,相同维度组合在不同时间中的映射地址相等,可单次扫描小颗粒时间累加得到大颗粒时间度量值。 图4 时间窗口聚合操作 目前已有流处理框架都是先存储数据片段再进行实时的OLAP操作,和文本所提实时计算和预存储模型的sketch cube不同。因此本文主要通过如下3个方面验证方法的有效性和正确性。 ·通过真实移动应用日志记录分析场景进行实验。分析sketch cube框架在不同时间窗口、不同裁剪模型参数和不同存储模型大小下的正确率、剪枝能力、框架吞吐效率;验证参数之间的影响和整体框架的有效性。 ·理论分析和比较sketch cube在存储空间上和其他存储模型的差异。 ·描述使用storm开源流框架搭建sketch cube的实现方式,并给出一个应用场景。 实验机器选择4台Dell服务器,16核IntelXeon 2.27 GHz,内存为32 GB,硬盘为4 TB,操作系统为Cenos 6.3,Java版本为JDK7。因为系统每秒接收流数据在1万条左右,采用Kafka和storm框架对数据进行处理,存储模型保存在MongoDB中。 数据集合:测试数据集来源于真实的移动嵌入式SDK中采集的应用记录,每条记录包含56个维度数值。本实验选择其中8个有代表性的维度进行OLAP统计,使用5%的均匀抽样(uniform sampling)方法运行 1 h,其含义和维度值的基数见表1。 表1 移动数据信息结构 对上述8个维度进行全立方体组合可得超过1017个数据单元。但通过分析可得,数据单元的分布是稀疏且偏斜的。在不同大小的时间窗口中,对维度组合的分布进行Zipfian的计算结果见表2。可得维度组合结果是偏斜的,因此,本实验数据符合使用sketch cube框架的条件。 表2 抽样移动数据分布 表2还表明数据是线性增加的,维度组合数量(DCIsize)随时间增加而趋于稳定,而偏斜因子和时间窗口长短无关。 表3给出了实验涉及参数的取值范围和缺省值。对于sketch cube所涉及的散列函数使用MurmurHash V3产生d个相互独立的散列族,时间窗口以20 min为基本单位,ACM选择m大小的裁剪模型,且在多组产生结果中进行分析和比较。 表3 实验参数 表4给出了ACM模型在3个不同参数下和全量计算模型(full count model,FCM)在包括吞吐量、裁剪能力和模型准确率方面的比较结果。 本节讨论ACM(m)裁剪方法在不同参数m下对sketch cube模型的剪枝能力。FCM表示统计全部维度组合,取m=(10,20,30,40,50)5个值,在3个不同时间长度中观察ACM的输出变化。如图5所示,ACM模型在不同参数下都具有10倍左右的裁剪能力且很显然参数值越小,保留的数据单元越少,裁剪能力越强。 表4 部分实验结果 图5 ACM剪枝实验 接着,需要测试剪枝模型的有效性和可用性,即裁剪后的模型是否仍然可以满足需求,而不会丢失很多有效数据。实验取20 min数据,分别统计ACM不同参数下提取DCI数量和裁剪后维度组合数量。如图6所示,ACM模型参数从10增加到50过程中,虽然DCI的数量有所提高,即计算得到的数据单元数量有明显的增加,但是裁剪后维度组合出现次数却基本相等。这说明数据是偏斜的,大量的高频数据反复出现,而长尾的数据只有少量出现。因此,ACM(10)基本包含了所有高频率的组合,在后续的框架构建和查询中,笔者使用ACM(10)作为裁剪模型。 图6 ACM裁剪模型效率 使用计数最小概要模型的sketch cube中保存的元素统计数据值要大于元素实际值,本实验使用平均百分比误差(mean percentage error,MPE)统计计数的准确率。计算式如下: 其中,at是实际值,ft是预测值,n是测试数据数量。 图7展示sketch cube中的存储空间大小和ACM参数对MPE的影响。取10 min数据,在不同存储宽度中比较4类模型的MPE值。ACM(m)中m越小,裁剪能力越强,模型准确率越高。随着存储空间的增大(即w参数的变大),所有模型的准确率都有所提高,这是因为存储空间的增加可以减少散列的碰撞概率,从而提高模型的准确率,但ACM整体准确率在任意存储模型下都较FCM有明显提高。 图7 w和ACM(n)对MPE的影响 图8 显示存储空间、结果集大小和MPE之间的关系。top-N从大到小排序,从横轴看,频率越高的数据单元,其MPE值越小,准确率越高。如在1 021宽度的存储模型中,ACM (10)模型对前20的高频数据单元的统计错误率为1%左右,而FCM的错误率超过20%。随着top-N的变大,MPE值也上升,说明sketch cube产生的数据单元是偏斜的。在不同的系统应用中,可以选择合适的存储空间大小和计算结果大小,如需要计算的top-N较大,则需要使用较小的ACM和较大的存储空间w。 接着计算模型的吞吐计算能力,因为运行时间受分布式框架节点数据和数据传输影响较大,因此吞吐能力测试在单节点上进行。取170 880条数据,在单节点中测量DCI计算时间和sketch cube计算时间。DCI时间表示计算数据单元标识集合的时间,sketch时间表示计算存入二维数组的偏移值的时长。测试取w=1 021。如图9所示,折线表示DCI集合的大小变化。从DCI运行时间和DCI集合变化曲线看,两者之间成正比关系,即模型的裁剪能力越强,DCI集合越小,DCI运行时间越短。对于任意模型,DCI运行时间远大于sketch计算时间。这些结论将被用于sketch cube模型的实现中。 图8 w和ACM(m)对MPE的增长趋势 图9 不同模型的运行时间 上述实验过程把每条记录可能的维度组合保存在类线性空间中。本实验将统计数据存储于MongoDB中,使用应用ID和时间窗口对数据检索。通过时间序列索引模型可知sketch cube支持任意时间窗口的组合。实验取3个不同的应用做实时查询,其效率分析见表5。 表5 查询效率分析 每个应用分别以10、20、30 min为长度,随机选择高维度值产生数据单元,进行OLAP查询。数据大小表示查询所涉及应用的日志数据大小。运行时间包括用时间序列索引找到相关的存储单元,通过数据单元标识模型产生唯一自然数标识,使用最小计数模型找到该数据单元的估计值所需的时间总和。从运行时间看,因为数据已经做了索引和统计,时间片长短和数据量大小对查询时间变化较小。同时查询时间都在毫秒级,因此可以满足实时查询的需求。 由于目前已有的对流数据的OLAP框架都是基于先存储数据,再进行分析的过程,和本文所述的实时统计框架有所不同。因此,本节主要理论分析数据在HashMap和sketch cube中的存储空间对比。假设,所有数据存储的基本单元都是整型,则HashMap的结构可以表示为HashMap 本节主要介绍使用storm开源流框架搭建sketch cube的过程。storm框架使用拓扑来描述不同计算节点之间的关系,根据前文的模块定义,把sketch cube的不同模块功能映射到storm的bolt中,且需要根据计算节点之间的I/O吞吐率和CPU计算量,调整节点的并发度,以达到系统整体的平衡。系统部署在第4.1节描述的4台服务器中,其结构如图10所示。 图10 storm实现sketch cube框架 系统分为3个部分,数据源负责收集相关多维度流数据信息,并保存在Kafka框架中;storm框架使用5个不同的计算节点,分别为输入数据接收、字典化处理、DCI计算,存储节点计算和存储节点。处理后的数据被保存在MongoDB数据库中。实时挖掘层(mining layer)从MongoDB中获得压缩后的数据单元统计值,并且进行相关在线分析模块(OLAM)操作得到结果返回给用户。 对例1中的场景,给定应用名称和时间片段,实时统计不同的数据单元下的度量值,本实验使用count计算数据单元的大小,最后选择和该时段这个应用最相关的top-50个数据单元。输出所在数据单元的维度值。对于给定应用appi,对于数据单元c的相关度(correlation)可以用式(21)所示: 其中,m表示数据单元度量值。 如对于流数据立方体c=((Wi-Fi,hz,Samsung),20140510081559),包含应用A的条数为200条,应用B为300条,则 对上述top-50的数据单元相关属性值进行统计,按每个属性值出现次数多少排序,并产生如图11所示的标签云图像。从图11可得,不同时间窗口下的标签云发生变化,这表明不同时间段的应用受众群体在发生变化。该类图像报表可以更好地帮助用户实时定位目标客户。 图11 标签云推荐 本文研究一种对海量流数据进行OLAM操作的框架sketch cube: ·提出数据单元标识模型及其改进算法; ·引入计数最小概要模型保存统计结果,并给出其适用场景; ·提出基于上下限的数据单元裁剪方法,提高存储效率和准确率; ·基于倾斜时间窗口的索引模型可快速计算任意时间片中的统计结果; ·真实数据集实验中,比较了相关参数对模型的影响,体现模型的优越性和可用性。 sketch cube只支持流数据分布型的聚合操作,在下一步工作中,将研究较为复杂的代数型和整体型聚合操作在流数据sketch cube模型中的应用。同时把计算过程中的性能瓶颈通过合理设计拓扑结构分散到不同机器节点中,以提高流数据的处理能力和稳定性。 1 Aggarwal C C.An Introduction to Data Streams.Data Streams.Springer US,2007 2 Hellerstein J M,Haas P J,Wang H J.Online aggregation.ACM SIGMOD Record,1997,26(2):171~182 3 Zhang X,Chou P L,Dong G.Efficient computation of iceberg cubes by bounding aggregate functions.IEEE Transactions on Knowledge and Data Engineering,2007,19(7) 4 Chen Y,Do ng G,Han J,et al.Multi-dimensional regression analysis of time-series data streams.Proceedings of the 28th International Conference on Very Large Data Bases,VLDB Endowment,Hong Kong,China,2002:323~334 5 胡文瑜,孙志挥,吴英杰.数据挖掘取样方法研究.计算机研究与发展,2009,48(1):45~54 6 De Rougemont M,Cao P T.Approximate answers to OLAP queries on streaming data warehouses.Proceedings of the Fifteenth International Workshop on Data Warehousing and OLAP,Maui,Hi,USA,2012:121~128 7 Babcock B,Shinath B,Mayur D,et al.Models and issues in data stream systems.Proceedings of the 21st ACM Symposium on PrinciplesofDatabase Systems,Madison,Wiscomsin,USA,2002:1~16 8 Chandrasekaran S,Cooper O,Deshpande A.TelegraphCQ:continuous dataflow processing for an uncertain world.Proceedings of the Conf on Innovative Data Systems Research,Asilomar,CA,USA,2003 9 Hetal T,Nikolay L,Hamid M,et al.SMM:a data stream management system for knowledge discovery.Proceedings of International Conference on Data Engineering, Hannover,Germany,2011:757~768 10 Rosenberg A L.Efficient pairing functions-and why you should care.International Journal of Foundations of Computer Science,2003,14(1):3~17 11 Zhang D,Zhai C,Han J,et al.Topic modeling for OLAP on multidimensional text database:topic cube and its applications.Stat Anal Data Min,2009,2(56):378~395 12 Ding B,Zhao B,Lin C,et al.Topcells:keyword-based search of top-k aggregated documents in text cube.Proceedings of International Conference on Data Engineering (ICDE),Long Beach,USA,2010:381~384 13 Lin C,Ding B,Han J,et al.TextCube:computingirmeansures for multidimensional text database analysis.Proceedings of the 8th IEEE International Conference on Data Mining(ICDM),2008:905~910 14 Liu X,Tang K Z,Hancock J,et al.A text cube approach to human,social and cultural behavior in the Twitter stream.LNCS 7812,2013:321~330 15 Cuzzocrea A.Retrieving accurate estimates to OLAP queries over uncertain and imprecise multidimensional data streams.Proceedings of the 23rd International Conference on SSDBM,Portland,OR,USA,2011 16 Aggarwal C C.Managing and Mining Sensor Data.New York:Springer US,2013 17 张进,邬江兴,刘勤让.4种技术型Bloom Filter的性能分析与比较.软件学报,2010,21(5):1098~1114 18 Cormode G,Hadjieleftheriou M.Finding frequent items in data streams.Proceedings of the VLDB Endowment,2008,1(2):1530~1541 19 Considine J,Hadjieleftheriou M,Li F,et al.Robust approximate aggregation in sensor data management systems. ACM Transactions on Database Systems(TODS),2009,34(1) 20 Han J,Kamber M,Pei J.Data Mining Concepts and Techniques.Elsevier Ltd,2012 21 Cormode G,Muthukrishnan S.An improved data stream summary: the count-min sketch and its applications. J Algorithms,2005,55(1):58~75 22 Cormode G,Muthukrishnan S.Summarizing and mining skewed data streams.Proceedings of SDM,Trondheim,Normay,2005 23 Giannella C,Han J,Pei J,et al.Mining frequent patterns in data streams at multiple time granularities.Next Generation Data Mining,2003(212):191~212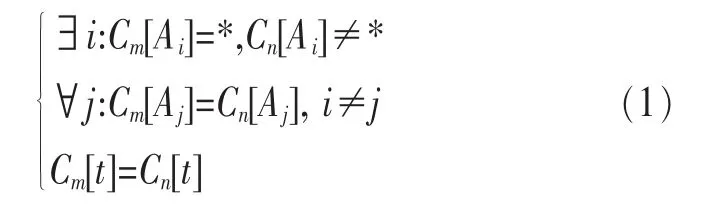

2.2 流数据立方体问题描述
3 sketch cube框架结构
3.1 数据单元标识算法
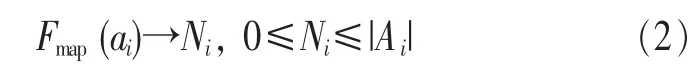
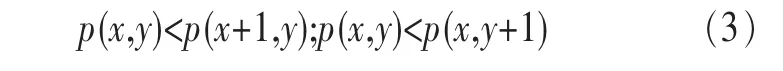
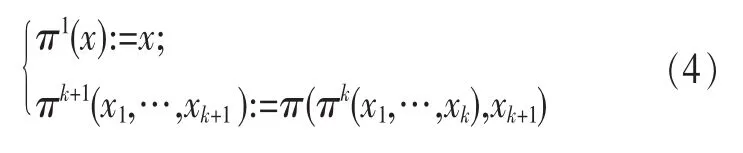
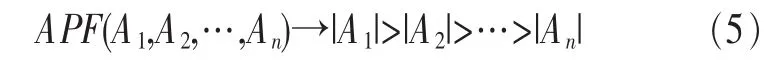
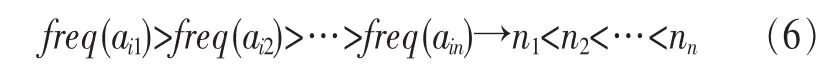
3.2 存储结构描述

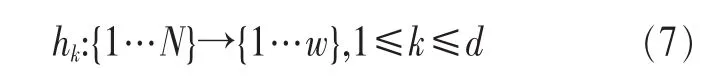
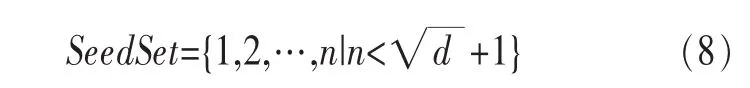

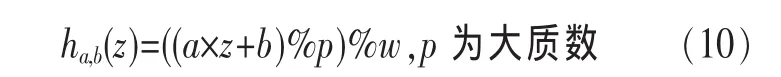
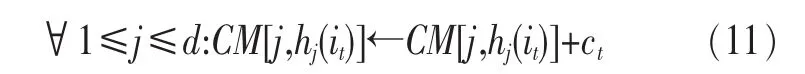
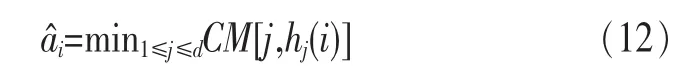


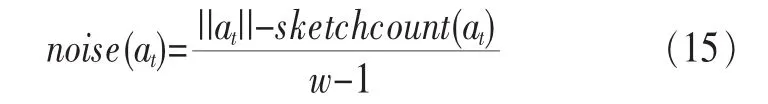
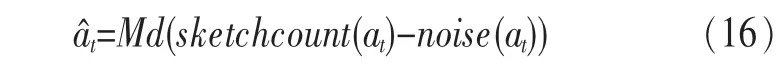
3.3 裁剪模型
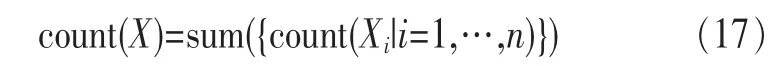
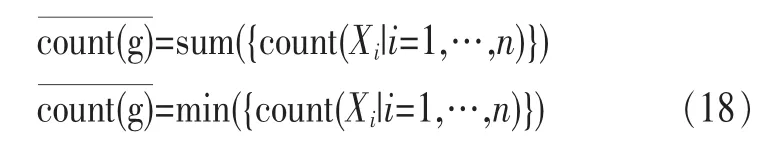
3.4 改进统计模型
3.5 时间序列索引描述
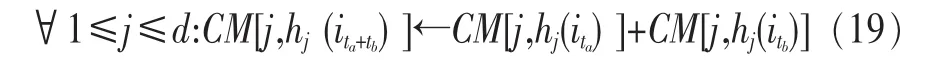
4 实验结果与分析
4.1 实验环境和数据描述

4.2 sketch cube计算性能
4.3 存储空间和误差
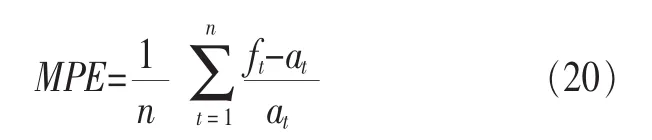
4.4 吞吐能力和计算时间比较
4.5 实时挖掘效率
4.6 空间效率
5 sketch cube平台构建过程
5.1 系统结构
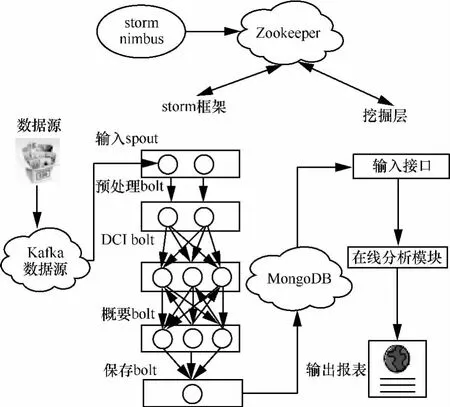
5.2 相关示例
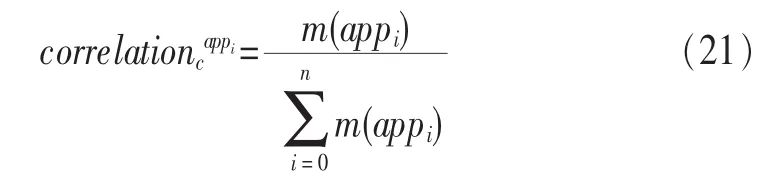
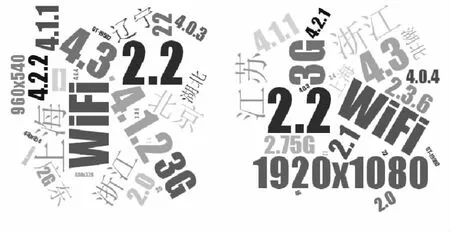
6 总结和展望
