基于Markov模型的福清市土地利用和覆被变化动态研究
2014-09-28唐南奇
陈 青,谢 钊,唐南奇
(福建农林大学资源与环境学院,福建 福州350002)
土地利用和覆被变化(Land Use and Land Cover Change,LUCC)作为“国际地圈生物圈计划”(IGBP)和“国际全球环境变化人文因素计划”(IHDP)等研究的核心领域之一,近年来受到越来越多专家学者的关注[1]。土地利用和覆被变化是一个动态演变过程,建立模型是对其进行动态研究的有效手段,亦是深入了解其变化机制和动力的重要途径[2]。常用于LUCC 研究的模型有:灰色模型、回归分析模型、Markov 模型、系统动力学模型、人工神经网络模型和元胞自动机模型等[3-4]。Markov 模型作为一种经典的预测模型,在LUCC 研究中应用最广泛。目前,关于土地利用和覆被变化的研究主要集中在城市及区域尺度上,如戴靓等[5]通过解译江苏省2000年和2008年的遥感影像,得到南京市辖区在这两个时期的土地利用数据,然后采用Markov 模型模拟预测南京市2016年的土地利用趋势。近年来也有一些专家将Markov 模型应用于县域尺度的土地利用变化研究,如朱萌等[6]在对武功县土地利用和覆被动态研究中,通过Markov 模型预测了武功县未来12 a 土地利用和覆被格局的动态演化趋势,且预测结果通过了模型效应系数的检验,说明将Markov 模型用于县域尺度的土地利用变化模拟是可行的。此外,还有部分学者将Markov 模型引入到其他模型之中,利用Markov 模型的优势弥补其他模型的不足,以提高相关模型模拟的可靠性及精确度。如吴季秋等[7]将Markov 模型与CA 元胞自动机模型耦合成CA-Markov 模型,利用Markov 长期预测的优势以及元胞自动机模型模拟复杂空间演变的优势,从土地利用适宜性原则与生态保护的角度对海南省八门湾的土地利用变化进行动态预测,结果表明人类活动尤其是相关土地政策在很大程度上影响着八门湾的土地利用变化趋势。
福清市地处海峡西岸经济区中部沿海,位于闽江口金三角经济圈南翼,东临台湾海峡,是环南、北太平洋两大经济繁荣圈的交接点。近年来随着海峡西岸经济区的全面建设,福清市城市建设和经济发展飞速,人地矛盾不断加剧,土地利用和覆被变化显著。研究利用2009年和2012年福清市土地利用现状矢量化数据,在ArcGIS、Matlab 等软件的支持下,建立Markov 模型对该地区的土地利用和覆被变化进行模拟预测,分析福清市土地利用和覆被变化的演化特点,以期对福清市合理利用和保护土地资源具有现实意义和参考价值。
1 Markov 模型预测的基本原理
Markov 模型预测是一类特殊的随机过程,它是由俄国数学家马尔科夫(A.A Markov)于1907年提出来的,该随机过程最大特点是具有无后效性[8]。无后效性是指某动态系统在T+1 时刻的状态只与T 时刻的状态有关,而与T 时刻之前的状态无关,不受T 时刻之前的状态所影响[9]。将Markov 模型应用于预测土地利用和覆被类型的动态变化趋势是非常合适的,因为土地利用和覆被类型变化是受人为和自然因素共同影响的,而这些影响因素又具有随机性、不确定性,使得土地利用和覆被类型的变化也成为一种随机运动过程。Markov 模型预测土地利用和覆被变化的基本原理,具体而言是在利用不同历史时期土地利用类型转移矩阵生成区域土地利用和覆被类型变化转移概率矩阵的基础上,预测某一特定情景下未来土地利用变化的趋势[10-11]。
研究表明,转移概率矩阵的确定是成功应用Markov 模型的关键[12]。土地利用和覆被类型转移概率是指在土地利用变化的过程中,某一土地利用类型在下一时刻转化为其他类型的可能性。由各土地利用状态的转移概率组成的矩阵P,即为转移概率矩阵。该矩阵可以定量地说明不同土地利用类型间的相互转化情况及转移速率,其数学表达式为:

式中:n 表示研究区土地利用和覆被类型的数目;Pij表示土地利用/覆被类型由i 转化为j 的概率。该矩阵的每一个元素需要同时满足以下两个条件:

如果已知土地利用和覆被类型系统中n=0 时的初始状态矩阵那么经过n 次转移后的状态矩阵为:

式中:P(n)表示初始状态土地利用/覆被类型概率矩阵经n 步转移后的概率矩阵,经过n 步转移后的系统状态概率矩阵为A(n)=A(n-1)P=A(n-2)PP=…=A(0)Pn,所以P(n)= Pn。由此可见,由初始状态矩阵和转移概率矩阵可以确定任何时刻的系统状态概率矩阵。
2 建模过程及趋势预测
2.1 基础数据的获取及处理
研究所用基础数据来源于福清市2009年和2012年土地利用变更调查数据。参照我国《土地利用分类》国家标准(CB/T 21010-2007),并结合土地修编现状分类标准以及福清市土地资源的具体情况和研究目的,将福清市土地利用和覆被类型划分为9 大类,分别为:耕地、园地、林地、草地、建设用地(包括商服用地、工矿仓储用地、住宅用地、公共管理与公共服务用地及水利设施用地)、交通用地、水域(水库水面及河流水面)、其他农用地(农村道路、坑塘水面及沟渠)和特殊及未利用地(未利用地包括内陆滩涂、沿海滩涂及裸地)。借助ArcGIS软件,对福清市2009年和2012年的土地利用变更调查数据进行矢量化处理并进行数据融合,获取福清市2009年和2012年各土地利用和覆被类型的面积,见表1。

表1 福清市2009/2012 年各土地利用和覆被类型面积(hm2)

表2 福清市2009年各土地利用和覆被类型向2012年的转化情况(hm2)
在Arcgis 软件中对两个时期的数据进行空间叠置分析,得到转移的各用地类型及属性数据,获取2009年各土地利用和覆被类型向2012年的转化情况,见表2。
2.2 转移概率矩阵的建立
2.2.1 初始状态矩阵的确定 将土地利用和覆被类型划分为一系列相互转化的状态,各状态在系统中所占的比例即每种土地利用类型面积占全部土地利用类型面积的百分比作为各状态的初始概率,从而形成初始状态矩阵A(0)。统计福清市2009年各土地利用类型的面积,进一步计算得到各覆被类型的面积百分比,从而形成初始状态矩阵A(0)(表3)。
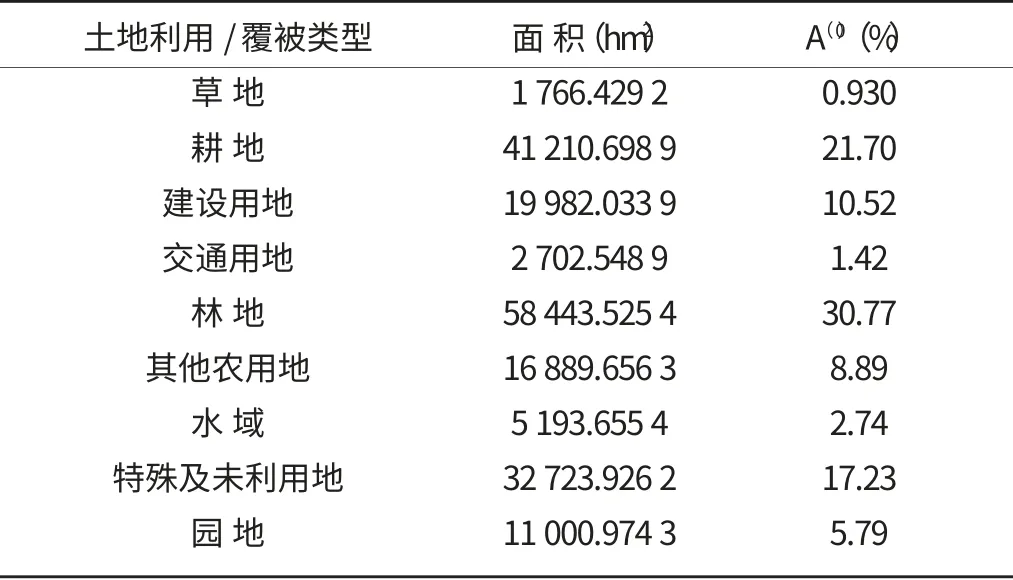
表3 初始状态矩阵A(0)
2.2.2 转移概率矩阵的确定 根据福清市2009年到2012年各用地类型的面积转移情况,以年为基本时间单位,求出时间段内某类土地利用和覆被类型的年平均转移概率。如研究区2009年草地中有部分到2012年变为耕地、建设用地、交通用地、其他农用地、特殊及未利用地和园地等,后者的面积占2009年草地总面积的比例再除以年数,即为其年平均转移概率。将草地转化为其他土地利用和覆被类型的概率作为第一行,耕地转化为其他土地利用和覆被类型的概率作为第二行,依次类推,便构成了初始状态转移概率矩阵P,见表4。
2.3 动态模拟及检验
借助MATLAB R2013a 平台,以1 a 为一个步长,根据公式①、②建立Markov 预测模型。由此可模拟预测出初始年份(2009年)后各时期的土地利用和覆被类型的转移概率和对应的转移概率矩阵。如通过计算n=3 的转移概率矩阵,可以模拟得到福清市2012年各土地利用/覆被类型的转移概率矩阵,见表5。
由表5 的模拟结果,结合表3 中的数据可获得福清市2012年各土地利用和覆被类型面积的预测值,将计算得到的预测值和2012年的实际值进行对比(表6),在SPSS18.0 软件中对预测值和实际值进行配对样本T 检验,设置置信水平为95%,结果显示:t=0.386,df=8,双侧P=0.709>0.05,即预测值与实际值之间并无显著性差异,表明通过Markov 模型模拟和预测福清市土地利用和覆被类型的动态演变趋势是可行的。

表5 2012年福清市土地利用和覆被类型的转移概率矩阵

表6 2012年福清市土地利用和覆被类型面积的实际值与预测值 (hm2)
2.4 变化趋势预测
对模型检验后,在保持当前干扰因素不变的前提下,在MATLAB R2013a 平台上编程依次输入n=6、11、16、21,运用Markov 模型进行预测,计算得到2015年、2020年、2025年和2030年福清市各土地利用和覆被类型的面积比例,见表7。

表7 2015~2030年福清市各土地利用和覆被类型的面积比例预测结果 (%)
3 结果与分析
由表7 可知,福清市未来18 a 内,耕地、林地、其他农用地、特殊及未利用地、园地等呈逐年减少趋势,而建设用地、交通用地则呈逐年上升趋势,这与该市前期土地利用/覆被类型变化趋势相似。在减少的用地类型中,耕地减少幅度较大,由2015年的21.30%下降到2030年的20.46%,减少的面积主要转化为了建设用地和交通用地;特殊及未利用地减少幅度次之,由2015年的16.95%下降至2030年的16.38%,主要是其中的未利用地转化为了建设用地和交通用地;林地由2015年的30.67%降至2030年的30.45%,减少的部分主要转化为了耕地和建设用地;其他农用地由2015年的8.76%下降至2030年的8.48%,主要转化为了耕地、建设用地和交通用地等;园地由2015年的5.73%下降至2030年的5.59%,减少面积主要转化为了草地和建设用地。在增加的土地利用类型中增加幅度最大的是建设用地,由2015年的11.38%上升至2030年的13.17%,主要由耕地与特殊及未利用地转化而来;其次是交通用地,虽然在各覆被类型中所占的面积较少,但一直处于增长状态,由2015年的1.56%上升至2030年的1.84%;此外,水域和草地所占的比例虽有变化但变幅较小可以忽略,可认为其没有变动,表明福清市的河流水域及草地得到了有效的保护。综上分析可知,按照当前的发展趋势,在未来的18 a 中,福清市城市建设用地将会不可避免的占用大量农林用地及未利用地。福清市建设用地和交通用地的持续增加说明该市的经济发展态势良好,但耕地与特殊及未利用地的减少也说明这种良好态势是以粮食安全和生态保护为代价的。
4 结论与建议
研究以2009年和2012年福清市不同土地利用类型之间的相互转化数据为基础,利用Matlab 编程Markov 模型对福清市2012年后的土地利用和覆被类型的变化趋势进行预测。模型预测结果与实际情况基本吻合,这说明将Markov 模型用于县域尺度土地利用和覆被格局变化趋势的预测是可行的。
根据Markov 模型预测福清市土地利用和覆被类型动态变化趋势,结果显示该市耕地、林地、其他农用地、特殊及未利用地比例呈逐年减少趋势,而建设用地和交通用地则呈逐年增加趋势。这表明随着福清市城市的建设和经济的发展,建设用地对土地的需求与农林用地保护之间的矛盾将日渐突出。该结果应引起相关政府部门的高度重视,并采取切实有效的措施,如耕地占卜平衡、城乡建设用地增减挂钩、节约集约利用建设用地及严厉打击违法违规用地等,既保证经济发展又保障生态粮食安全。
Markov 预测模型建立的前提是假定外界干扰因素不变,由已知时期的土地利用变化情况推导出其未来的发展演化趋势,但实际情况中人为干扰仍然是影响福清市土地利用和覆被类型变化的主要因素,所以该预测模型存在一定的局限性。在今后的研究中应尽力把对土地利用影响较大的相关土地政策考虑进去,使研究结果更加准确可靠;此外,在建立Markov 预测模型时,时间尺度是建立该模型的一个重要环节,不同的时间尺度可能会导致不同的模拟结果。研究仅采取2009年和2012年两个时期的数据,时间尺度有点小,在今后的研究中应尽量选取较长及较多的时间尺度来进预测研究。
[1]杨维鸽.基于CA-Markov模型和多层次模型的土地利用变化模拟和影响因素研究——以陕西省米脂县高西沟村为例[D].西安:西北大学硕士学位论文,2011.
[2]韩春建,吴克宁,刘德元,等.基于马尔科夫模型的郑州市郊区多方案耕地保有量预测[J].土壤,2011,43(3):453-458.
[3]夏小梅,陈柯林.基于遥感与GIS的LUCC及马尔科夫过程趋势预测——以重庆市南岸区为例[J].水土保持研究,2009,16(5):19-24.
[4]刘慧璋,郭青霞,王曰鑫,等.基于Markov的山西岔口小流域土地利用变化预测[J].山西农业大学学报,2012,32(1):53-57.
[5]戴 靓,吴绍华.基于Markov模型的南京土地利用时空变化研究[J].资源开发与市场,2011,27(5):417-420.
[6]朱 萌,马孝义,刘雪娇.基于马尔科夫模型的武功县土地利用/覆被动态变化研究[J].水土保持研究,2013,20(5):64-68.
[7]吴季秋,俞花美,肖 明,等.基于CA-Markov模型的海湾土地利用动态监测[J].环境工程技术学报,2012,(6):531-539.
[8]Hulst R.On the dynamics of vefetation:Markov chains asmodels of successi on[J].Vegetation,1979,40(1):3-14.
[9]GengX M,LiL.Markov process functional-sinfinan ceand in surance[J].Applied Mathematics,2009,24(1):21-26.
[10]喻 峰.基于Markov-CA的土地利用变化预测研究[J].国土资源情报,2009,(4):38-46.
[11]罗 平,姜仁荣,李红旮,等.基于空间Logistic和Markov模型集成的区域土地利用演化方法研究[J].中国土地科学,2010,(1):31-36.
[12]郜鲁豪,徐 旌.基于Markov模型的安宁市土地利用预测[J].云南地理环境研究,2010,22(2):87-89.
