基于粒子群优化的电动汽车再生制动模糊控制

周云鹏， 赵 韩，2， 江 昊，2

（1.合肥工业大学 机械与汽车工程学院，安徽 合肥 230009；2.合肥工业大学（马鞍山）高新技术研究院，安徽 马鞍山 243000）

本文针对电驱动汽车的回馈制动控制问题，应用粒子群优化算法，以回收制动能量为目标函数，对制动能量回馈的模糊控制规则进行优化。在最为常见的一般制动工况下进行仿真，与未用粒子群优化的模糊控制器进行比较。

1 再生制动控制策略

1.1 制动力分配原则

综合考虑汽车制动的稳定性和能量回收高效性，本文提出了前后轮制动力分配区间［8］，该分配区间如图1所示。该制动力的分配原则为：当车速高于门限值，制动强度低于给定值（0.1g），电机通过传动系统提供制动力，机械制动不工作；当制动强度高于指定值（0.1g）时，电机制动力与机械制动力同时作用于前轮，前后轮机械制动力按比例分配。制动系统为提高制动效率，装有一个比例阀，根据制动强度改变前后制动器制动力的比值，使之接近理想制动力分配曲线［9］。当紧急制动时，ABS启动，再生制动力不再参与工作。该制动力的分配必须满足ECE法规制定的最小后轮制动力分配曲线M线、最佳制动力分配曲线I线和在某一地面附着条件下，前轮抱死后轮不抱死时前后轮制动力关系曲线f线的限制，其中路面附着系数φ取0.7。采用制动力分配原则，只需对原车的机械制动系统的前后轴制动分配比例进行适当调整，以满足设计的前后制动力分配比例，而系统结构和机械制动力矩的控制方式可以保持不变。

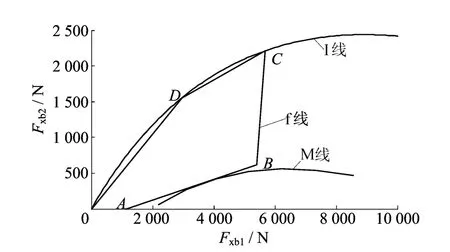
图1 复合制动力分配区间

1.2 基于模糊逻辑的再生制动力分配

模糊控制器的作用是根据车辆的行驶状态确定电机制动力的大小，实现制动能量的高效回收，同时满足汽车制动的安全性和舒适性的要求。

（1）模糊控制器结构。根据影响再生制动的因素设计三输入一输出的模糊控制器，推理方法选用Mamdani推理。选取制动踏板深度、电池荷电状态（SOC）、车速作为模糊控制器输入量；以电机制动的参与程度，即电机制动力矩占最大可用电机制动力矩的比例作为模糊控制器输出量。

（2）语言变量的选取。制动踏板深度与制动安全性关系紧密，控制器的制动踏板深度输入量分为5个模糊子集｛VS，S，M，B，VB｝。为了保护电池和防止电池过充，电池的SOC值应控制在80%以下；电池SOC输入量分为5个模糊子集｛VL，L，M，H，VH｝；考虑到车速与制动能量回收的关系，车速分为7个模糊子集｛VL，L，LM，M，HM，H，VH｝；电机再生制动力的比例为模糊控制器输出量，分为11个模糊子集｛KM0，KM1，KM2，KM3，KM4，KM5，KM6，KM7，KM8，KM9，KM10｝。

2 粒子群优化模糊规则

2.1 粒子群优化算法

粒子群优化算法［10］首先初始化产生一群随机粒子，然后迭代寻找最优解。在每次迭代中，粒子通过跟踪2个极值不断更新，即个体极值历史最优解（pBest）和全局最优解（gBest），然后根据速度和位置公式更新粒子的速度和位置，公式为：

《周礼·考工记》有云“天有时，地有气，材有美，工有巧。合此四者然后可以为良”。中国传统文化中，木材便是这通天接地，感应时气，材美更可巧工的良材，是中国传统建筑营造的理想之材[1]88。其历史悠久，应用广泛，在不同地域环境及民族文化的影响下呈现出多样的风格特点。然而在中国近现代文明进程中，随着新的建筑材料建造技术的涌现，传承发展数千年的木结构体系在中国逐步淡出，广大乡镇居民也转为采用砖、混凝土等材料建造新的居所。

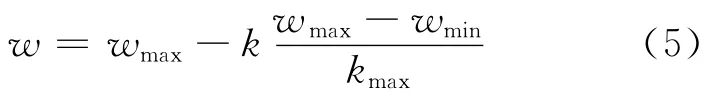
其中，kmax为总的迭代次数；wmax为最大权重；wmin为最小权重。在每次迭代中，算法根据粒子的适应值不断更新pBest和gBest的值。

2.2 粒子编码

采用粒子群算法优化模糊控制器的模糊规则时，需要把整车优化目标有关的控制变量集中编码，由于车速很低与电池荷电状态很高时不回收制动能量，因此所需优化的模糊规则为120个。利用粒子群算法进行模糊规则的优化整定，将需要优化的模糊控制参数编码成粒子码串［x1，x2，…，x119，x120］。粒子的每个变量均用整数表示，变量取值范围为1～11。

2.3 适应度函数的选择

将再生制动回收的能量优化目标函数、制动稳定性与电池的充电功率限制作为约束条件，则适应度函数为：

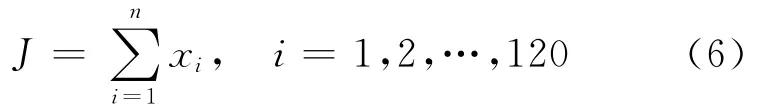
其中，xi为通过约束条件的模糊规则。

约束条件为：

其中，Tmmin、Tmmax分别为电机的最小和最大转矩；wmmin、wmmax分别为电机的最小和最大转速；SOCmin、SOCmax为电池的最小和最大荷电状态；Pchg－max为电池允许的最大充电功率；Preg为再生制动功率。

2.4 优化步骤

基于粒子群优化的模糊控制器结构如图2所示。

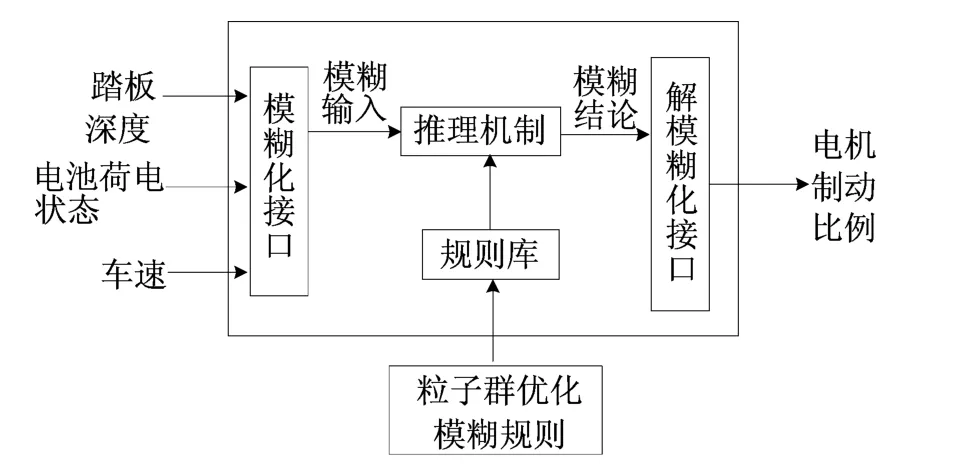
图2 基于粒子群优化的模糊控制器结构

根据制动踏板深度、电池荷电状态和车速，利用粒子群优化算法对模糊控制器的规则库进行优化。优化步骤如下：

（1）对120个变量进行编码，并确定粒子的搜索范围和最大速度。

（2）初始化每个粒子的速度与位置。

（3）将每个粒子的历史最优值存储在pBesti中，将每次迭代的最优值存储在gBest中，作为全局最优解。

（4）由（1）式、（2）式更新粒子各维的速度，由（3）式、（4）式更新粒子各维位置。

（5）更新（5）式的惯性权重。

（6）对每个粒子进行解码，更新模糊规则，计算适应值，并根据适应值确定是否更新pBesti与gBest。

（7）转到步骤（3）进行迭代，直到达到最大迭代次数或gBest更新步长小于指定阀值。将gBest解码作为模糊控制器的最优模糊规则。

3 仿真结果分析

在车辆行驶的大部分时间里，多数制动为一般制动。因此，针对一般制动工况选择初始车速分别为90、60、30km／h，初始荷电状态为20%、50%、80%进行仿真分析。

在一般制动工况下，车速、制动减速度、利用附着系数随时间的变化如图3所示。

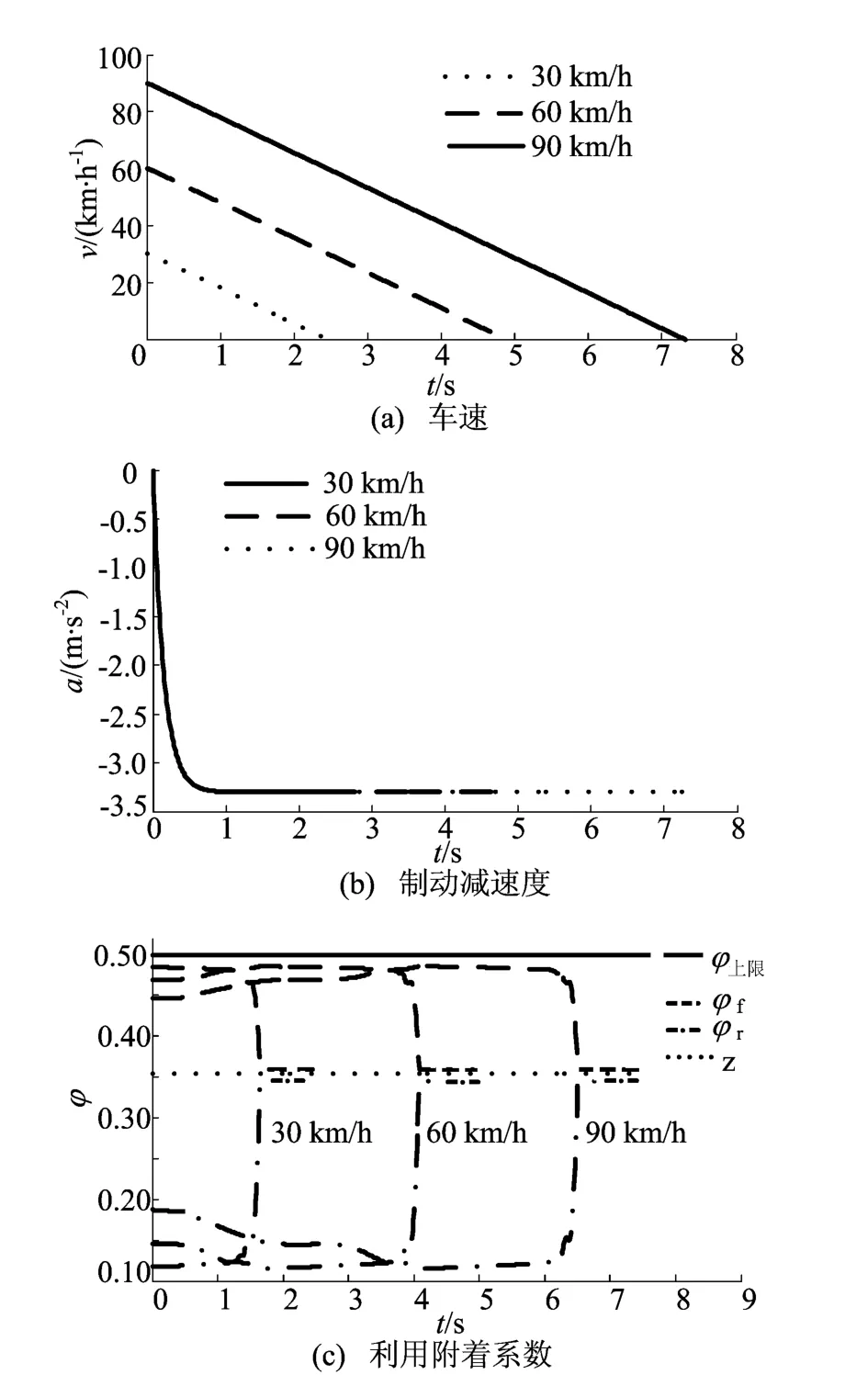
图3 不同初始车速的制动情况

仿真结果表明，电机参与制动时，地面附着系数利用不充分，但依然满足ECE法规要求。

不同初始SOC下的电机制动功率如图4所示，由图4可以看出，在SOC偏低与较高时，电池的允许充电功率比较低；在SOC较为适中时，电池的允许充电功率最高。模糊控制器能很好地控制电机制动功率低于电池峰值充电功率，避免了可能由于充电功率较高对电池的损害。

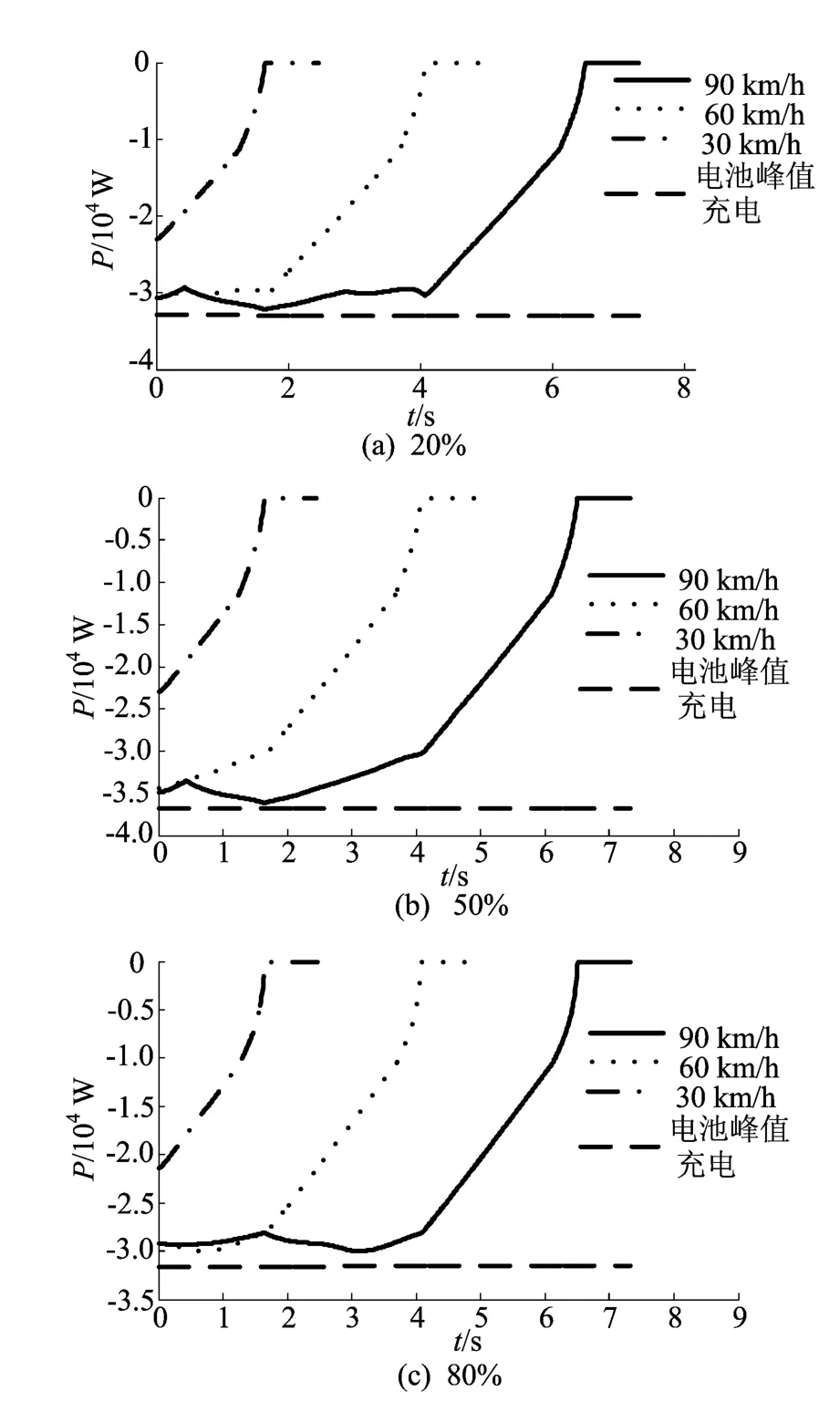
图4 不同初始SOC时的再生制动功率

粒子群优化的模糊控制器与普通模糊控制器制动能量回收的比较见表1所列。

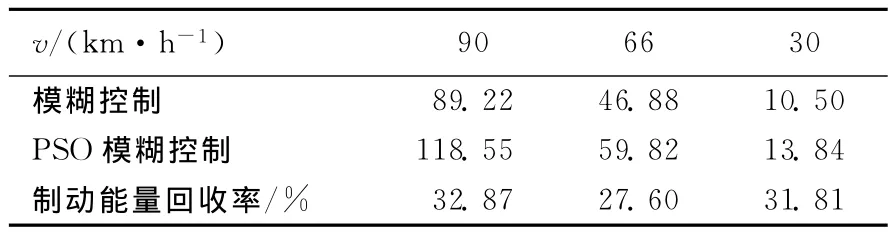
表1 制动能量回收效率对比 kJ

由表1可以看出，在不同车速下，粒子群优化的模糊控制器能量回收有明显的提高。

4 结束语

在保证制动安全性的条件下优先进行制动能量回收，根据该原则，本文应用粒子群算法对模糊规则进行优化。在不同的初始车速与SOC值下，对一般制动工况进行了仿真分析，仿真结果显示粒子群优化的模糊控制器，能量回收效果有明显提高，制动力的分配也满足ECE法规要求。综上，应用粒子群优化算法，为模糊控制器的模糊规则的制定提出了一种较为科学、客观的方法。

［1］Gao Y，Chu L，Ehsani M.Design and control principles of hybrid braking system for EV，HEV and FCV［C］／／Vehicle Power and Propulsion Conference，2007：384－391.

［2］刘 辉，王伟达，何 娇，等.基于模糊控制的混合动力电动车再生制动系统的建模与仿真［J］.汽车工程，2012，34（1）：51－56.

［3］彭 栋，殷承良，张建武.基于模糊控制的并联式混合动力汽车制动控制系统［J］.吉林大学学报：工学版，2007，37（4）：756－761.

［4］张邦基，于德介，邓元望.基于模糊逻辑的并联式混合动力电动汽车 能量控制系统［J］.汽车工程，2009，31（6）：496－502.

［5］Zhang Z，Xu G，Li W，et al.Regenerative braking for electric vehicle based on fuzzy logic control strategy［C］／／Mechanical and Electronics Engineering（ICMEE），20102nd International Conference on，Vol 1.IEEE，2010：319－323.

［6］赵国柱，滕建辉，魏民祥，等.基于模糊控制的电动汽车低速再生 ABS研究［J］.中国机械工程，2012，23（1）：117－121.

［7］吴启迪，汪 镭.智能微粒群算法研究及应用［M］.南京：江苏教育出版社，2005：106－113.

［8］刘红亮，董学平，张炳力.电动汽车再生制动控制策略的研究［J］.合肥工业大学学报：自然科学版，2012，35（11）：1484－1487，1532.

［9］赵国柱.电动汽车再生制动稳定性研究［D］.南京：南京航空航天大学，2006.

［10］Esmin A A A，Lambert－Torres G.Generate and optimize fuzzy rules using the particle swarm algorithm［C］／／Systems Man and Cybernetics（SMC），2010IEEE International Conference on.IEEE，2010：4244－4250.