多种类型电动汽车接入配电网的充电负荷概率模拟
2014-09-27周念成熊希聪王强钢
周念成,熊希聪,王强钢
(重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
0 引言
环境污染的加剧和一次能源的日益短缺,使得电动汽车在各国得到广泛的推广应用。然而电动汽车的大量普及,将对配电网带来冲击,增加发输配电系统的压力[1-3]。电动汽车的大规模充电行为使得其并网时必将对配电网的电能质量、网络损耗、设备利用率等方面产生显著影响[4-7]。针对电动汽车作为移动式储能单元的时空不确定性,文献[8]基于电动汽车的开始充电时刻、行驶里程和充电功率这3个随机变量的概率分布,结合美国居民出行调查NHTS(National Household Travel Survey)统计数据,建立了公务和私用2类电动汽车的充电负荷需求模型;文献[9]考虑了4种不同类型的电动汽车及其相应的充电行为,提出采用蒙特卡洛模拟抽取初始荷电状态SOC(State Of Charge)、起始充电时间的电动汽车充电负荷计算方法;文献[10]根据实时电价和电动汽车蓄电池的初始SOC曲线,建立了改进的电动汽车充电负荷需求模型。以上文献均仅针对纯电动汽车,尚未建立混合电动汽车的充电负荷概率模型。此外,现有方法假设开始充电时刻和初始SOC相互独立,未考虑初始SOC对用户充电行为的作用。
本文针对混合动力电动汽车的电荷消耗和电荷维持2种模式切换运行的特点[11],改进初始SOC的概率模型。考虑蓄电池充电时间长度对汽车充电开始时刻进行选择,并引入电动汽车充电数量抽样,建立多种类型电动汽车充电负荷的概率模型。通过某地的负荷数据和IEEE 34节点配电网算例,应用所提出的电动汽车充电负荷概率模型进行充电概率模拟,分析在工作日和休息日下不同渗透率的电动汽车充电负荷对配电网负荷的影响及换电池充电方式不同比例下对配电网负荷的影响。
1 改进的电动汽车充电负荷概率模拟方法
电动汽车的充电负荷模拟时须根据电动汽车的类型来选择各抽样环节的概率模型及其参数,再根据不同区域各类电动汽车数量逐台叠加,从而得到电动汽车接入配电网的负荷需求。常规概率模型仅针对纯电动汽车,认为电动汽车接入电网后随即开始充电,未考虑实时车流量概率分布,且假设开始充电时刻和初始SOC相互独立,不能计及初始SOC对用户决定是否进行充电的影响。由于不同类型电动汽车的开始充电时间、初始SOC等充电参数不尽相同,相应的充电负荷随机特性差别较大。为研究三者对充电负荷的影响,本文采用图1所示的电动汽车4层次分类结构。其中,由于以换电池充电方式为主的运营模式处于实验发展阶段,涉及生产商多,电池标准难以统一,目前换电池主要在排放量较大的公交车中推广[12]。
针对多种类型的电动汽车接入配电网,本文改进了电动汽车负荷概率模拟结构,如图2所示(改进部分由虚线方框表示)。在行驶里程概率抽样时,先判断电动汽车是属于纯电动汽车还是混合动力电动汽车,以选择不同的行驶里程概率模型。根据电动汽车充电方式(常规、快速及换电池)和能源供给方式(蓄电池类型),可确定不同类型电动汽车蓄电池在不同充电方式下的充电功率和SOC特性[8],见图3和图4。图中锂电池充电过程中的功率基本恒定且起始和结束阶段较短;铅酸电池采用常规充电时峰值功率为6.50 kW,而采用快速充电时峰值功率为45.80kW。结合初始SOC抽样,确定充电时间长度概率模型。

图1 电动汽车的层次分类结构Fig.1 Structure of EV hierarchical classification
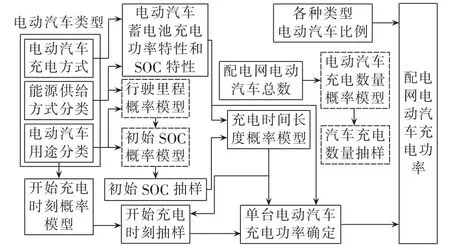
图2 电动汽车充电负荷概率模拟结构框图Fig.2 Block diagram of EV charging load probability simulation

图3 不同类型电动汽车的充电功率特性Fig.3 Charging characteristics of different EV types

图4 不同类型电动汽车的SOC特性Fig.4 SOC characteristics of different EV types
在改进模型中还加入电动汽车充电数量抽样来模拟电动汽车的行驶状态,避免处于行驶状态的电动汽车导致充电负荷模拟误差。
2 电动汽车充电负荷概率模型
2.1 初始SOC和充电时间长度的概率模型
纯电动汽车日行驶里程dp与汽车分类相关,根据NHTS统计数据可知其满足对数正态分布[13]:

其中,μ=ln[E(X)]-0.5 ln[1+D(X)/E2(X)]、σ2=ln[1+D(X)/E2(X)]分别为对数均值和方差,E(X)和 D(X)分别为日行驶里程样本数据的均值和方差,X为服从对数正态分布的随机变量dp,x为X的可能取值。
混合动力电动汽车具有电荷消耗和电荷维持2种模式,处于电荷消耗模式时电动汽车的行驶耗能全部由蓄电池提供,一旦蓄电池能量耗尽后即转入电荷维持模式,此时由燃料提供全部能耗。本文采用混合动力电动汽车行驶里程dt和蓄电池续航里程db(db表示蓄电池充满后能维持的最大里程)2个随机变量表征混合电动汽车的日蓄电池耗能里程dh为:

假设随机变量dt和db相互独立,可得dh的概率分布函数 Fdh(x)和概率密度函数 fdh(x)为:
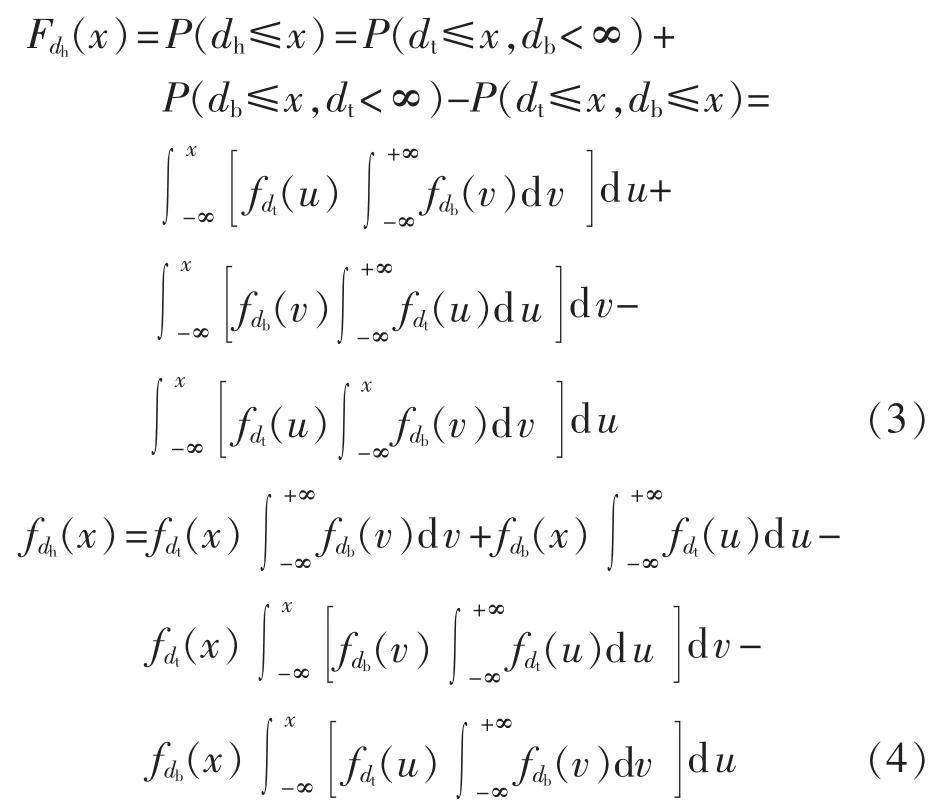
其中,fdt(x)和 fdb(x)为服从式(1)的对数正态分布概率密度函数。表1为基于NHTS 2009数据库的不同类型电动汽车的行驶里程参数。

表1 行驶里程和单位行驶距离能耗的均值和标准差Tab.1 Mean and standard deviation of trip distance and energy consumption rate
电动汽车蓄电池的SOC具有随机性,其由前次充电后的SOC和相邻2次充电的行驶里程所决定。文献[14]对电动汽车SOC随行驶里程的变化特性进行了研究,两者近似成线性关系但仍呈现一定分散性。假设电动汽车蓄电池充满后才开始行驶,则可得蓄电池的初始SOC如下:

其中,d为电动汽车的日行驶里程;h为单位行驶距离能耗量;η=0.672 为汽车行驶效率常数[15];α 为相邻2次充电的间隔天数,其中公交和出租车分别采用每天和每半天充1次电,而公务和私用车为每2天充1次电;En为蓄电池额定容量;Ec为蓄电池的日能耗。
将不同 SOC 下的行驶里程数据[14]代入式(5)可计算单位行驶距离能耗量h估算值,如图5所示,可见h满足正态分布。不同类型电动汽车的单位行驶距离能耗正态模型参数见表1[11]。初始SOC的概率密度函数fSOC(x)与2个随机变量h和d的乘积相关,根据表1数据采用数值方法可得不同类型电动汽车的初始SOC概率分布,如图6所示。其中公交车和出租车在概率密度峰值处所对应的SOC小于公务车和私用车,图6(a)和(b)对比可知混合动力电动汽车初始SOC的均值高于相同用途类型的纯电动汽车。
设电动汽车蓄电池SOC从0%充电至100%过程中充电功率随时间变化曲线为P(t),则不同初始SOC下蓄电池充电至满电量所需的充电时间Tc为:
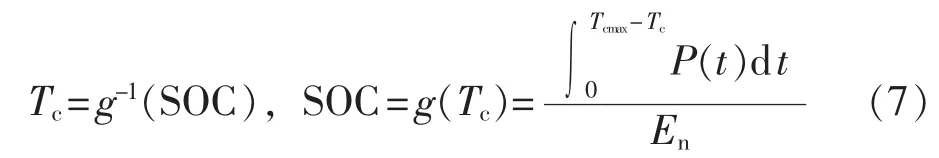
其中,Tcmax为蓄电池SOC从0%充电至100%所需时间。由于各类电动汽车的充电功率尚未形成统一表达式,本文在充电功率模拟时根据实测数据采用分段线性插值方法来计算不同初始SOC对应的充电时间长度,数据参考图3、图4。

图5 单位行驶距离能耗量正态概率图Fig.5 Normal probability plot of energy consumption rate

图6 不同类型电动汽车的SOC概率分布Fig.6 Probability distribution of SOC for different EV types
2.2 开始充电时刻的概率模型
a.常规和快速充电。
考虑到汽车蓄电池的初始SOC也将影响用户对于充电开始时刻的选择,设电动汽车的开始充电时刻满足均匀分布[8-9],且出租车或公交车的上下班时间分别为 Ton、Toff,午休时间为[Tm1,Tm2]。 为了保证蓄电池充满后才开始行驶的约束,令Tc≥Tm2-Tm1的电动汽车只在夜晚进行充电,其开始充电时刻ts概率分布如下。
若 Ton≤Tc,则:
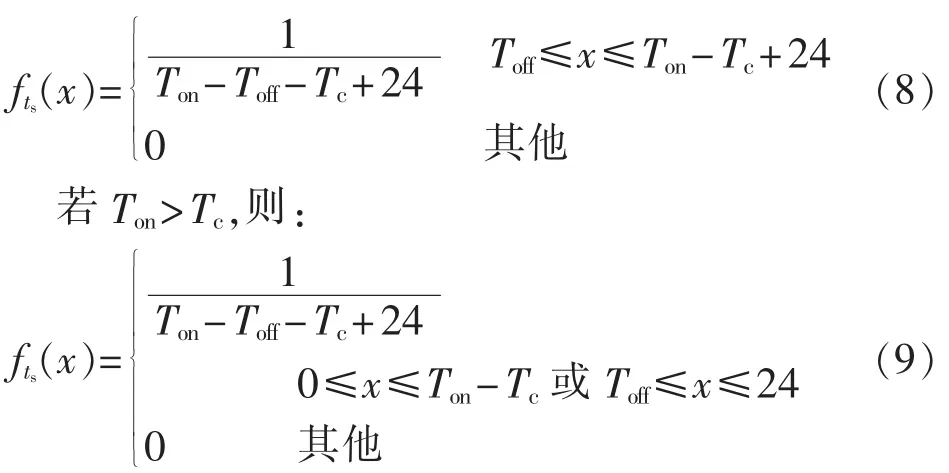
其中,Tc由电动汽车蓄电池类型、充电方式和初始SOC决定。对于Tc<Tm2-Tm1的出租或公交电动汽车,其开始充电时刻ts概率分布如下。
若 Ton≤Tc,则:

若 Ton>Tc,则:

公交和出租车的 Ton、Toff、Tm1、Tm2分别设为 06:00、22:00、10:00、14:00 和 04:00、23:00、11:00、14:00。 而由于公务车和私用车仅在夜晚时段进行充电,其开始充电时刻的概率模型如式(8)、(9)所示,取公务和私用车用户的 Ton、Toff分别为 08:00、20:00 和 08:00、18:00。
b.换电池充电。
对于换电池充电方式,需根据配电网负荷变化和日电价曲线来选择低谷负荷时段进行有序充电[16]。若换电池方式的充电时间区间为[Ta1,Ta2]、[Tb1,Tb2],则其开始充电时刻ts的概率分布为:

其中,ηa+ηb=1.0 分别为充电区间[Ta1,Ta2]和充电区间[Tb1,Tb2]的概率值。换电池充电方式的充电功率灵活性强,且受充电时间的约束也相对较小,需根据实际需要来进行选择。
2.3 电动汽车充电数量的概率模型
电动汽车充电功率模拟时处于行驶状态的电动汽车由于未进入停车场/充电站,不参与充电负荷模拟。图7为典型的行驶汽车比例系数曲线[17],图7(a)中工作日的汽车行驶比例呈双峰特性,峰值区间为[06:00,08:00]和[16:00,18:00],采用下式计算不同类型电动汽车的充电数量:

其中,N为配电网区域的电动汽车总数;A和Nc分别为各种类型电动汽车的比例和充电数向量;ηtr为行驶汽车比例系数。由文献[18]可知1 d中不同时刻电动汽车停泊比例1-ηtr服从正态分布,采用正态分布对ηtr进行抽样可得该时刻的车辆停泊比例。
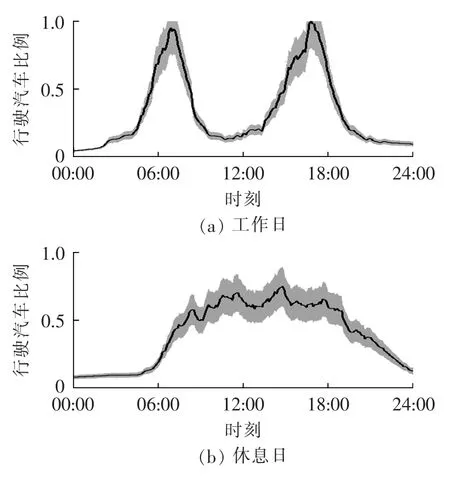
图7 电动汽车行驶比例系数Fig.7 Proportional coefficient of travelling EVs
通过前述概率模型能够对接入多种类型电动汽车的配电网充电负荷进行蒙特卡洛模拟,模拟中采用各个时刻配电网充电负荷的方差系数作为收敛控制条件[19]。研究中认为电动汽车仅在充电时间段较短的中午才可能进行快速充电。此外,充电时间长度将决定用户对充电时间的选择,对于具备快速充电功能的电动汽车须计算采用常规、快速充电的充电时间Tcn和Tcr,当中午的充电时间段Tm2-Tm1≤Tcn时其在中午进行快速充电,否则为延长蓄电池寿命采用常规充电。
3 电动汽车充电对配电网负荷的影响
以IEEE 34节点算例为基础,如图8所示划分为工业、商业及居民用电负荷三大类区域,图9为某地区配变实测负荷数据,其中工业负荷包含机械、食品及制药区域。设配电网区域的汽车数量为3540辆,根据电动汽车渗透率(配电网区域的电动汽车数量占总汽车数量的比例[8])来计算电动汽车总数。

图8 电动汽车充电负荷接入IEEE 34节点配电网算例Fig.8 IEEE 34-bus distribution feeder with EV charging load
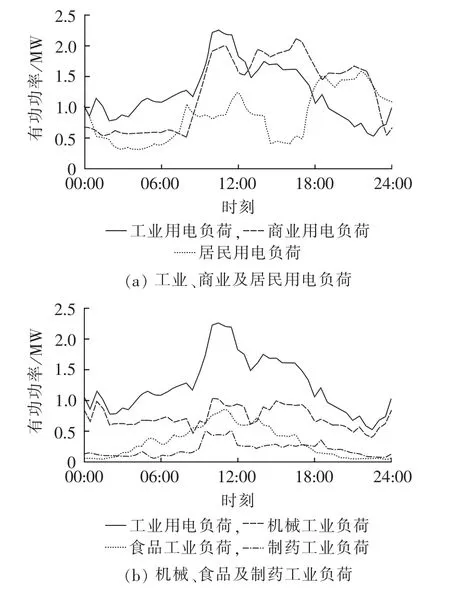
图9 某地配电网负荷曲线Fig.9 Load curves of a distribution network
不同区域充电站(桩)的比例为:工业用电区域中机械、食品、制药分别占18%、12%、8%,居民用电区域占26%,商业用电区域占36%。不同能源供给方式电动汽车比例为:纯电动汽车占30%,混合电动汽车占70%。不同充电方式电动汽车比例为:常规占60%,快速占30%,换电池占10%。不同用途电动汽车比例为:公交车占50%,出租车占20%,公务/商务车占20%,私用车占10%。采用铅酸蓄电池和锂离子/镍基蓄电池的电动汽车各占一半,对于不同用电区域的充电负荷按照相应充电站或充电桩等比例分配。根据图9不同负荷的特点,设置不同区域换电池充电站的充电时间区间参数。其中商业区域仅含2个充电区间,其他区域均包含3个,具体数据如表2所示。
3.1 工作日和休息日电动汽车的充电负荷影响
电动汽车渗透率分别为0%、10%和20%时,可得正常工作日和休息日配电网节点800的总负荷曲线如图10所示。在正常工作日中,当渗透率为10%时配电网最大负荷加重,负荷峰值时刻仍然出现在[10:00,12:00]间;而当渗透率升至20%时负荷曲线在22:00时出现新的高峰,此时电动汽车接入使总负荷峰值由5.1 MW升高至6.9 MW,对配电网造成更大的冲击。
与图7中的休息日负荷曲线相比,在白天和夜晚的电动汽车充电负荷高峰时段工作日负荷大幅高于休息日负荷,而凌晨的充电时段两者差别较小。由图 7 可知[05:00,08:00]和[15:00,18:00]时段休息日处于停泊状态的汽车比例高于工作日,但因该时段充电负荷较小,休息日负荷仅略高于工作日充电负荷。
3.2 换电池充电方式比例变化的充电负荷影响
设常规和快速充电的电动汽车保持2∶1不变,逐渐增加换电池充电方式的比重,可得图11和图12所示电动汽车渗透率20%时工作日的配电网总负荷和商业区负荷曲线。图11中换电池比例为10%和50%时峰值负荷分别增加了17.8%和6.2%,且在10%比例下总负荷在21:30出现新峰荷6.014MW。当换电池比例增至100%时,峰值负荷仅仅增加了2.7%,且夜间低谷负荷区域得到明显填补。图12中换电池比例为10%和50%时对应的峰值负荷分别增加了12.3%和6.8%,当配电网区域所有电动汽车都采用换电池充电方式时,商业负荷峰值接近于原始负荷峰值。由于换电池充电的可控性,随着换电池比例增加,商业负荷峰谷差逐渐减小,原始负荷低谷时段得到有效填补。

表2 不同区域换电池充电站充电时间区间Tab.2 Charging duration of battery swap station for different regions
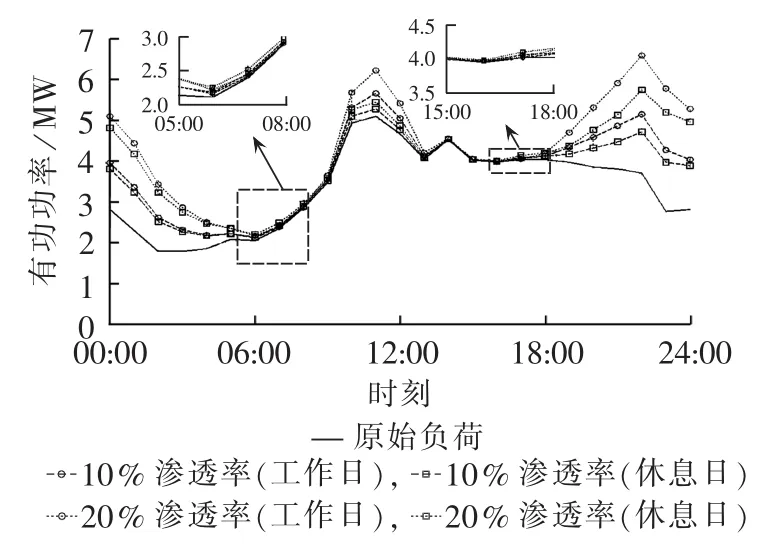
图10 工作日和休息日配电网总负荷曲线Fig.10 Total load curves of distribution network for workday and holiday

图11 不同换电池比例时配电网总负荷曲线Fig.11 Total load curves of distribution network for different battery swap rates

图12 不同换电池比例时配电网商业负荷曲线Fig.12 Commercial load curves of distribution network for different battery swap rates
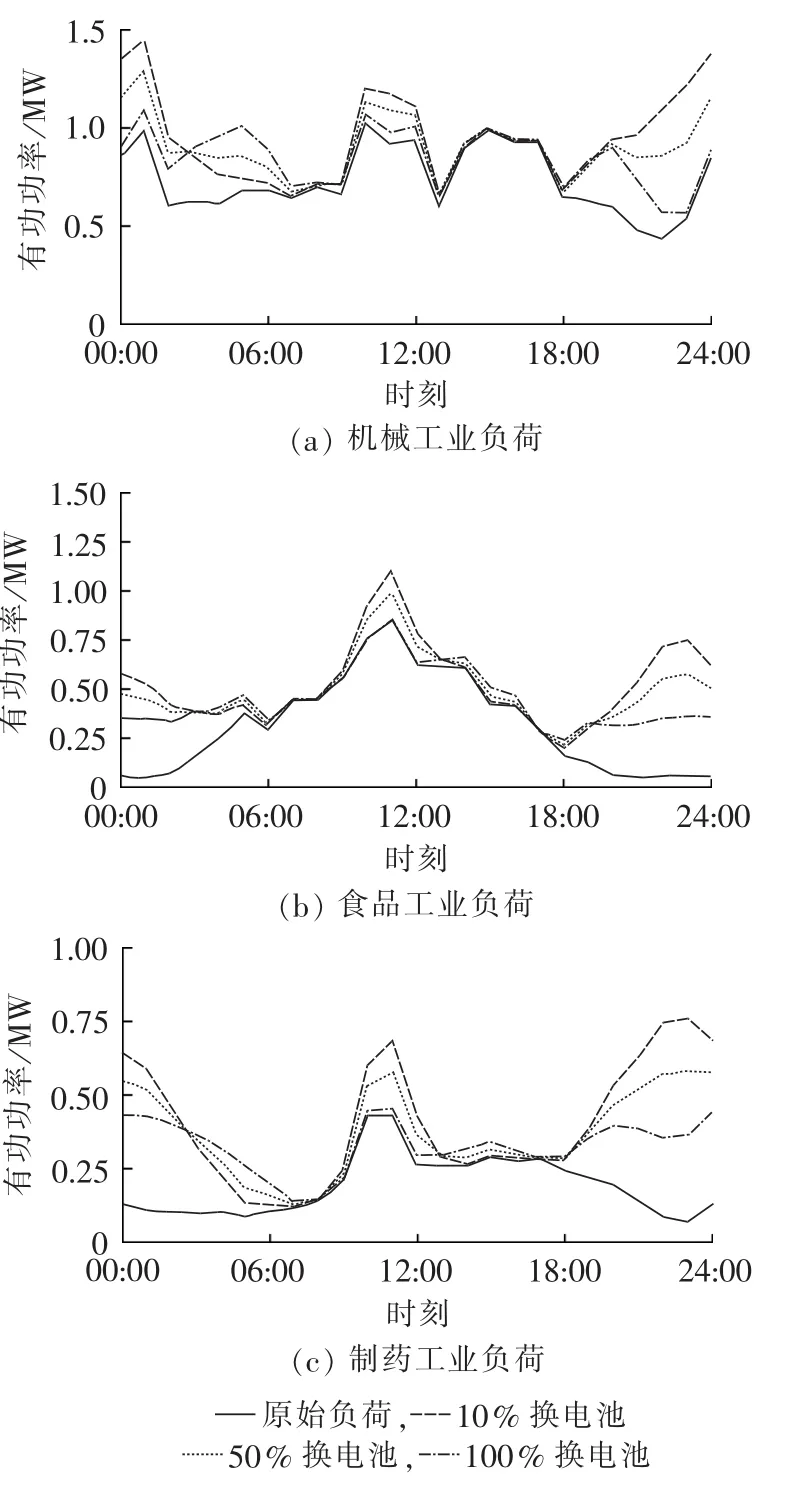
图13 不同换电池比例时配电网3种工业负荷曲线Fig.13 Three types of industrial load curves of distribution network for different battery swap rates
图13所示为工业区域3种不同类型负荷在不同换电池比例情况下的负荷曲线,由图可知采用换电池方式的电动汽车比例增加,充电负荷填谷作用越明显,从而使负荷变化更加平缓。根据不同类型负荷曲线的变化特点,制定换电池电动汽车充电方案,能够有效减小原始负荷的波动变化,同时抑制充电负荷对配电网的影响。
图13(a)和(c)中机械和制药工业的原始负荷较为平滑,换电池比例增加虽然降低负荷峰值,但仍可能在原始负荷低谷时段产生新的峰值。因此在充电站建设规划时,应尽量将充电站设置在负荷峰谷差较大的用电区域。同时,提高换电池电动汽车比例,以充分利用充电负荷填补负荷低谷的潜力,降低电动汽车规模化对配电网带来的负荷冲击。
4 结论
不同类型电动汽车用户的驾驶行为和充电习惯决定了电动汽车充电负荷的时空随机特性。本文建立混合电动汽车接入配电网的充电负荷概率模型,提出多类电动汽车接入配电网的充电负荷需求概率模拟方法。通过IEEE 34节点配电网算例和实测负荷数据分析电动汽车充电负荷对配电网负荷的影响。结果表明,白天和夜晚的电动汽车充电高峰时段工作日负荷高于休息日负荷,而凌晨充电时段两者差别较小;换电池电动汽车比例增加能够有效减小充电负荷对配电网的影响。
