基于信息论准则的高光谱波段选择方法

范 超

（河海大学 计算机与信息学院, 江苏 南京 211100）

随着遥感成像光谱仪的发展,遥感成像由多光谱发展到高光谱(Hyperspectral)阶段,高光谱成像光谱仪在对目标进行成像的同时,对每个空间像元经过色散形成几十个甚至上百个窄波段以进行连续光谱成像,因此高光谱遥感图像可以看为一个由空间维和光谱维组成的多维图像立方体。与传统多光谱遥感影像相比,高光谱影像不仅在信息丰富程度方面有了极大的提高,在处理技术上,对该类光谱数据进行更为合理、有效的分析处理提供了可能。它的覆盖范围从可见光到近红外光(400～2 500 nm),每一个波段宽度大约10 nm左右,得到每个像元完整连续光谱曲线的同时,也增加了图像数据量,且波段之间相关性很强,因而包含了大量的冗余信息,这给后续的处理带来了一定的难度。

1 技术背景

在实际的应用过程中,高光谱遥感图像作为一个图像立方体[1](如图1所示),需要根据具体要求,在不改变图像原有特性的基础上对高光谱图像进行降维,以便提高后期处理效率。针对这个问题,可以采用波段选择的方法,从原始图像数百个波段中选取最能代表整体特征的波段组,以此来表示整个数据集。现有的波段选择方法在进行波段组合优选时主要从3个因素着手:

1)所选择的波段或波段组合信息含量大;

2)所选择的波段与波段之间相关性小;

3)所选择的波段与波段之间能使某些类别地物容易区分。

本文从信息论和波段间相关性这两个方面综合考虑,提出了一种采用粒子群优化算法(PSO)基于信息论准则的高光谱遥感图像波段选择方法,进行波段组合优选。

2 粒子群优化算法(PSO)

图1 高光谱图像立方体Fig.1 Hyperspectral remote sensing image cube

粒子群算法(particleswarmoptimization,PSO)是计算智能领域的一种群体智能的优化算法[2-3]。该算法最早由Kennedy和Eberhart在1995年提出的。PSO算法源于对鸟类捕食行为的研究,鸟类捕食时,找到食物最简单有效的策略就是搜寻当前距离食物最近的鸟的周围区域。PSO算法是从这种生物种群行为特征中得到启发并用于求解优化问题的,算法中每个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动经验进行动态调整,从而实现个体在可解空间中的寻优。

PSO算法首先在可行解空间中初始化一群粒子,每个粒子都代表极值优化问题的一个潜在最优解,用位置、速度和适应度值三项指标表示该粒子特征,适应度值由适应度函数计算得到,其值的好坏表示粒子的优劣。粒子在解空间中运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置,群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。粒子每更新一次位置,就计算一次适应度值,并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。

假设在一个D维的搜索空间中,由n个粒子组成的种群X=(X1,X2,…,Xn),其中第i个粒子表示为一个D维的向量Xi=(xi1,xi2,…,xiD)T,代表第i个粒子在D维搜索空间中的位置,亦代表问题的一个潜在解。根据目标函数即可计算出每个粒子位置Xi对应的适应度值。第i个粒子的速度为Vi=(Vi1,Vi2,…,ViD)T,其个体极值为Pi=(Pi1,Pi2,…,PiD)T,种群的群体极值为Pg=(Pg1, Pg2,…, PgD)T。

在每次迭代过程中,粒子通过个体极值和种群极值更新自身的速度和位置,即式(1)(2):

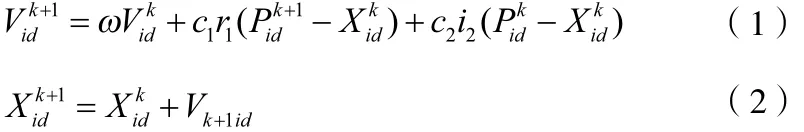
中,ω为惯性权重;d=1,2,…,D;i=1,2,…,n;k为当前迭代次数;Vid为粒子的速度;c1和c2是非负的常数,称为加速度因子;r1和r2是分布于〔0,1〕区间的随机数。为防止粒子的盲目搜索,一般建议将其位置和速度限制在一定的区间[-Xmax,Xmax]、[-Vmax,Vmax]。

3 基于信息论准则的高光谱波段选择方法

3.1 波段选择算法流程

根据高光谱遥感图像波段多、数据量大、波段间相关性强等特点[4],本文设计的高光谱遥感图像波段选择方法共分为四个阶段,如图2所示:1)图像预处理阶段;2)波段去相关分组阶段;3)波段优化组合阶段;4)分类验证阶段。

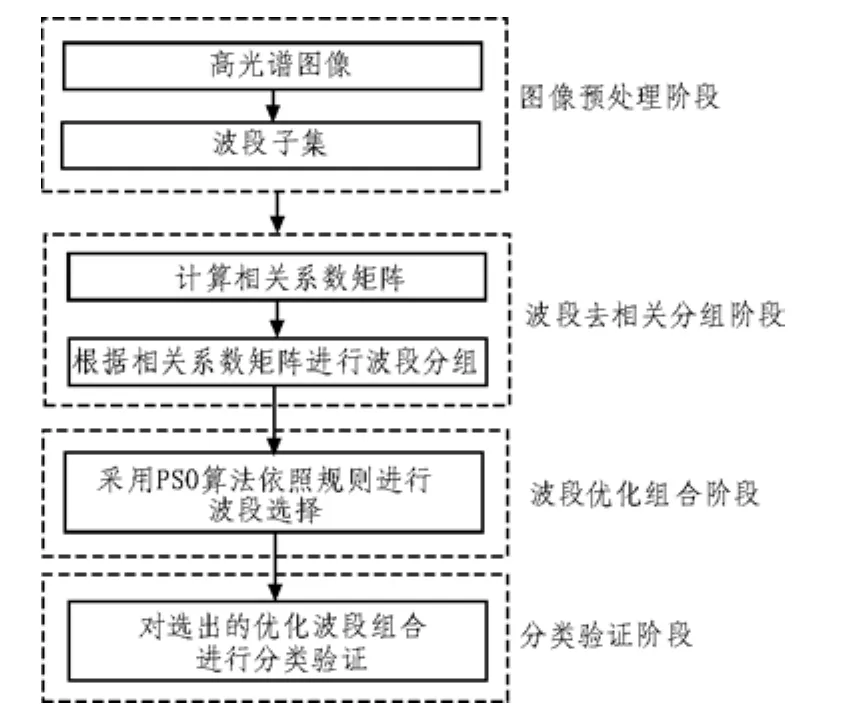
图2 波段选择法流程图Fig.2 Band selection algorithm flowchart

1)原始图像预处理

大气吸收、散射作用使得到达地表的辐射能力和到达遥感器的地物反射能量都出现衰减且大气本身作为散射体的上行散射辐射到达遥感器使得能量增加,但该辐射能量不带有任何地物信息。在图像预处理阶段,对原始高光谱图像进行辐射校正和几何校正,去除受噪声和水气污染较为严重的波段。

2)波段分组去相关

多波段图像间的相关性表示了每个波段图像在相同空间位置处的像素相关性,反应了波段之间的冗余,可用互相关系数进行评价,相关系数越大,相关性越强,波段间冗余越高[5]。波段i与波段j间的相关系数Rij可表示为:

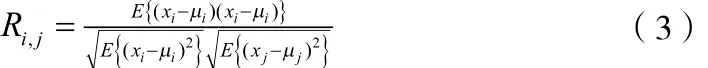
式中,xi,xj分别表示i,j波段上对应位置值,μi、μj分别为i , j波段平均值,E()表示函数的数学期望。

文中根据相邻波段间的相关系数变化曲线对经预处理的高光谱遥感图像进行波段分组。

3)波段优化组合

依照提出的基于信息论准则的高光谱波段选择方法,将波段的信息熵作为粒子群优化算法(PSO)的适应度函数,波段的适应度切合程度决定波段组合被选中的概率。在进行选择时,同时考虑波段与相邻前一波段之间的相关系数,选择信息熵大且相关系数较小的波段。

根据香农信息理论,熵可以用来表征信息量[6],它使总体平均意义上的概念,一幅8bit的图像P的每个像元所携带的平均信息量可以用熵H来表示:

其中,是图像中像素灰度值为i的概率。

3.2 基于信息论的高光谱波段选择方法步骤

粒子群优化算法(PSO)在进行多目标优化时,随着迭代次数的变化,粒子的速度和位置也发生变化,粒子的位置不断朝着较优位置变动,迭代若干次后获得最优解组合。速度更新公式中惯性权值ω决定着算法的全局搜索能力与局部搜索能力,本文为了兼顾算法的全局搜索能力与局部搜索能力,迭代过程中采用变惯性权值的方式,在每次迭代完成后,改变惯性权值ω的大小。算法中ω按照式(5)进行随机调整。波段优选方法详细流程如图3所示。

其中,rand( )为0～1之间的一个随机数。

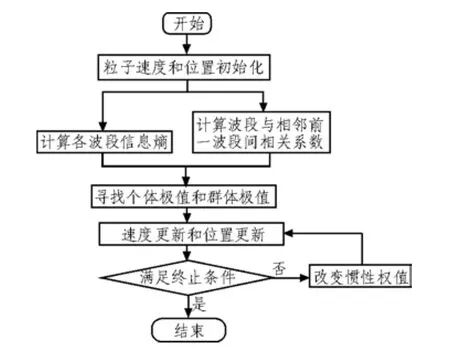
图3 波段选择详细算法流程图Fig. 3 Hyperspectral image band selection algorithm flow chart

整个算法详细步骤如下:

1)初始化粒子群,每个粒子由高光谱图像波段组合、惯性权值ω、加速因子C 3部分组成。初始种群中粒子随机生成3部分,初始种群的大小根据计算的复杂程度进行合理设置,保证初始种群中含有尽可能多的可能解;

2)根据波段的信息熵和与相邻前一波段间相关系数计算公式计算适应度值,求解最优解;

3)根据第2部分式(1)(2)更新粒子的速度Vi、位置Xi;

4)判断是否符合迭代停止条件,如未达到停止条件则改变惯性权值,跳至第3步继续迭代寻优。如达到迭代停止条件则结束搜索,输出最优解。

4 实验及其结果分析

4.1 实验设计

为了验证文中提出的基于信息量准则的高光谱波段选择方法的可行性和有效性,本文采用1992年6月利用AVIRIS传感器获得的印第安纳州西北部印第安农林高光谱遥感试验区的一部分图像进行试验。预先经过统计及计算去除受水气和噪声影响较为严重的波段(波段1-4、78、103-110、149-165、217-224),经处理后图像剩余179个波段,图4为第5、37、120三波段合成的R、G、B伪彩色图。整个实验在InterCORE 2.1 GHz CPU、内存为4G的计算机上运行,采用Matlab R2009编程实现。

图4 第5、37、120三波段合成的R、G、B伪彩色图Fig. 4 5、37、120tri-band synthesis of R、G、B pesudo-color diagram

4.2 波段分组

按照前章描述的处理过程,对经处理剩余的179个波段进行分组。根据式(3)计算波段间的相关系数,得到相关系数矩阵。如图5所示,相关系数矩阵具有分块的特点,且以对角线左右对称,图中灰度值越大,代表波段间的相关系数越大,相关性越强。表1为部分波段间的相关系数矩阵,从相关系数矩阵中分别获得首波段与波段间及相邻波段间的相关系数,如图6所示。结合图5与图6将179个波段划分为5个波段子集 :[1-33]、[34-75]、[76-91]、[92-129]、[130-179]。

图5 相关系数矩阵灰度图Fig. 5 Correlation coefficient matrix grayscale

4.3 波段优选

实验中,粒子群优化算法的参数设置如下:c1=c2=2,粒子速度的初始值为0,迭代次数设置为200,种群规模设定为50,个体速度最大值和最小值分别设定为5和-5。惯性权值ω按照式变动,当迭代次数达到预设200时,算法停止。经过算法搜索选取,获得波段组合[25,37,77,102,143]为最佳组合。

4.4 分类验证

为进一步评价采用本文提出的方法选出的最佳波段组合,对选出的最佳波段组合进行分类验证,并与使用等间隔划分波段方法进行比较。采用支持向量机(SVM)高光谱分类方法进行分类,经计算得到分类准确率达到91.0%,较采用等间隔划分波段方法有明显的提高。图7所示分别为原始地物定标图、使用按波段间相关系数分组方法分组分类图和使用等间隔分组方法分组分类图。

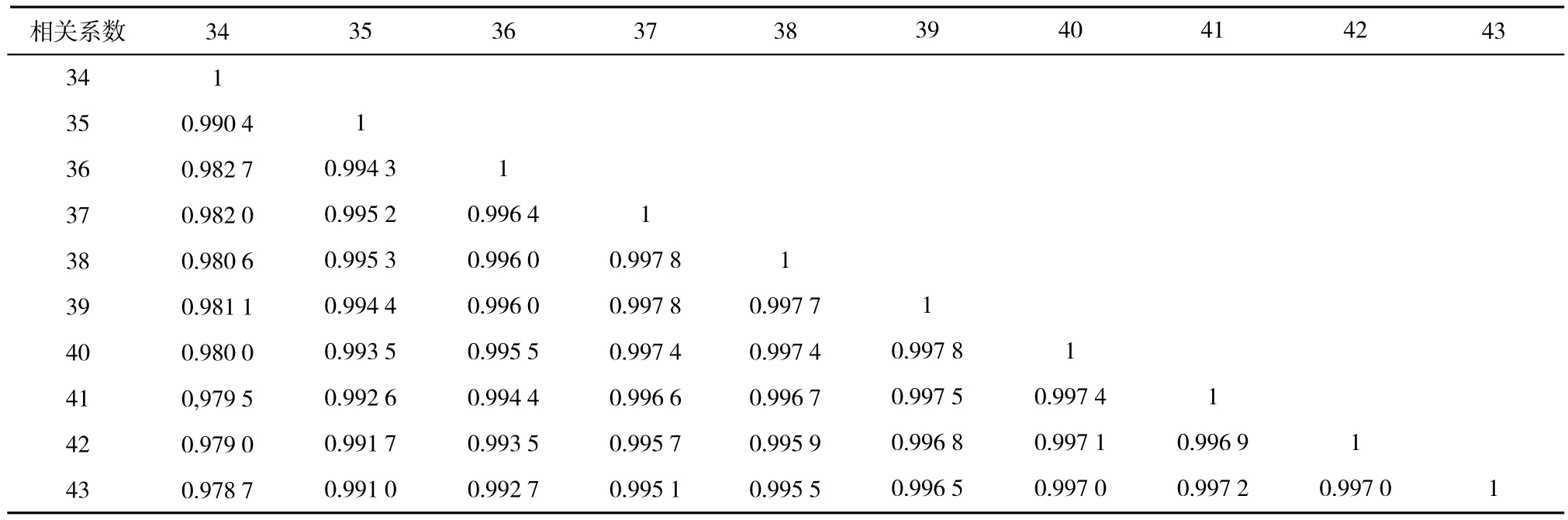
表1 部分波段间的相关系数矩阵Tab.1 Correlation matrix between the part of the band

图6 波段与首波段间及相邻波段间的相在系数图Fig. 6 Band and the first band and adjacent band correlation coefficient between Figure

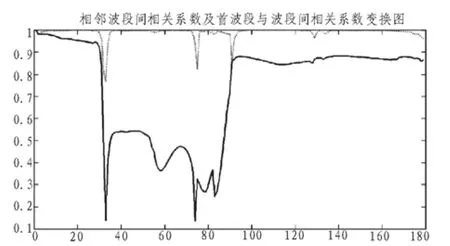
图7 分类结果对比图Fig. 7 Comparison of the classification results

5 结 论

在对高光谱图像进行处理时,图像降维是关键的处理步骤,近年来很多文献提出了相应的解决办法,本文在分析现有文献基础上,针对现有方法采用单一准则的片面性,结合高光谱图像波段间的相关系数,提出了一种基于信息量准则的高光谱波段选择方法。实验结果表明该方法对AVIRIS高光谱遥感图像波段选择的有效性。

文中虽然验证了对AVIRIS高光谱遥感图像进行波段选择时具有较高的效率,但对于其他的高光谱遥感图像未得到进一步的验证,还需要对不同类型光谱成像仪获得的图像进行实验与验证,这都需要进一步分析与研究。

[1]张兵,高连如. 高光谱图像分类与目标探测[M]. 北京:科学出版社,2010.

[2]Kennedy J,Eeberhart R C. Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Network s. Perth: IEEE Neural Networks Society,1995: 1942-1948.

[3]Ke nne dy J,Ebe rhart R C. A discrete binary version of the particle swarm Algorithm[C]//Proceedings of the World Multiconference on Systemic, Cybernetics and Informatics 1997.Piscataway: IEEE,1997:4104-4109.

[4]赵春晖,陈万海,杨雷. 高光谱遥感图像最优波段选择方法的研究进展与分析[J].黑龙江大学自然科学学报,2007,24(5):592-602.

ZHAO Chun-hui,CHEN Mo-hai,YANG Lei. Research advances and analysis of hyperspectral remote sensing image band selection[J]. Journal of Natural Science of Heilongjiang University,2007,24(5):592-602.

[5]苏红军,盛业华,杜培军. 自动子空间划分在高光谱影像波段选择中的应用[J]. 地球信息科学,2007,9(4):123-128.

SU Hong-jun,SHENG Ye-hua,DU Pei-jun. Study on autosubspace partition for band selection of hyperspectral image[J].GEO-INFORMATION Science,2007,9(4):123-128.

[6]卢健,彭嫚,卢昕. 遥感图像相关性及其熵计算[J]. 武汉大学学报:信息科学版,2006,31(6):476-480.

LU Jian,PENG Man,LU Xin. Relativity of remote sensing images and entropy calculation[J]. Geomatics and Information Science of Wuhan University,2006,31(6):476-480.