基于自蛇模型和小波分析的图像去噪

陈日红

（上海汽车技术中心(南京) 电子电器部，江苏 南京 210061）

图像在生成和传输过程中受各种噪声的影响，容易引起质量退化。为了后续更高层次的处理, 有必要对图像进行去噪。根据实际图像的特点和噪声的统计特征形成了多种图像去噪方法，例如维纳滤波、小波分析和偏微分方程等。小波分析具有快速变换和在时域、频域同时具有良好的局部化特性的特点，可以把图像结构和纹理表现在不同分辨率层次上，分析表明在滤除噪声的同时也会模糊图像边缘,使得图像质量得不到完美的改善[1-2]。因为噪声和边缘同属于高频信息，偏微分方程（PDE）的良好性质而得到研究人员的关注，其中以Perona 和Malik提出的各向异性扩散模型(P-M)最具代表性[3]。它将图像去噪转化为对偏微分方程的求解，基于偏微分方程去噪因其在保留图像边缘和消除噪声方面其主要思想是在去噪的过程中引入了边缘检测的步骤, 这样能兼顾去噪和保留边缘信息[4-5]。为了保护图像边缘,要求扩散方向只沿着平行于边缘的切线方向,也即垂直于图像梯度矢量方向进行,于是提出了方向扩散方程。自蛇模型与方向扩散类似，它由带有边缘停止函数的方向扩散项和具有图像增强功能的冲击滤波器两项组成[6]。本文将自蛇模型与小波分析相结合，提出基于自蛇模型和小波分析的图像去噪方法。

1 自蛇模型及数字实现

设u为图像的灰度值，div为散度，自蛇模型图像去噪方程如下[6]：

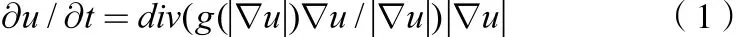
将式（1）展开为两项如下，第一项为带有边缘停止函数g(|▽u|) 的方向扩散Fdiff，第二项具有图像增强功能的冲击滤波器Fdiff，具体如下：

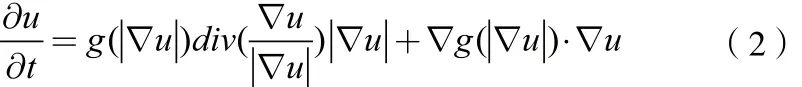
其中，上式边缘停止函数g(|▽u|) 的一般采用下式：

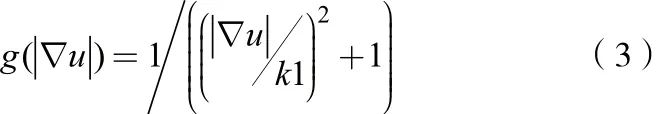
其中，k1为常数。在图像平坦同质区域其梯度很小，边缘停止函数近似为1，在边缘处梯度很大，边缘停止函数近似为0。为得到式（2）稳定的数字解，将散度div半点离散化并记为vi,j：

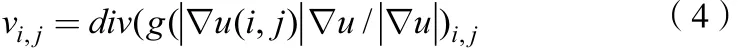
式(2)为Hamilton-Jacobi方程，采用迎风差分方案，即自蛇模型数字实现如下:

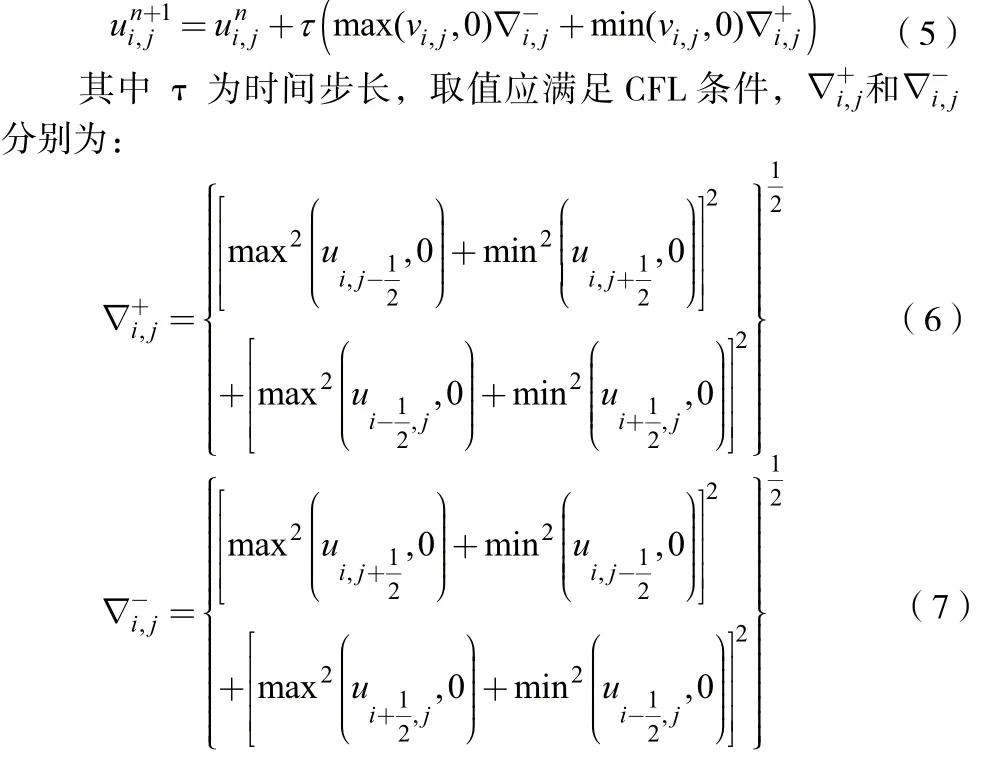
2 自蛇模型和小波分析的集成去噪

利用自蛇模型的偏微分方程对图像滤波，虽然在去噪的同时能尽量保持图像特征，但随着迭代次数增加，图像会越来越模糊。本文先对噪声图像进行自蛇模型滤波，再将其小波分解得到低频分量和三个高频分量。低频含有图像的主要信号特征，是原始图像的近似图像，为保留图像特征，该分量保持不变。高频分量含有图像的大部分噪声和边缘细节，再利用自蛇模型图像滤波去噪，最后对处理后的小波系数进行重构，得到对原信号的最佳恢复，从而形成偏微分方程和小波分析的集成图像去噪算法如图1所示。

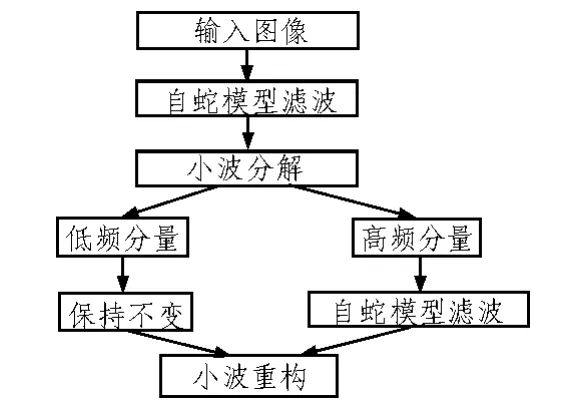
图1 自蛇模型和小波分析的集成去噪算法Fig.1 Structure of integrated denoising algorithm of self-snake and wavelet analysis

3 实验结果与讨论

为客观评价自蛇模型去噪算法（算法1）、2次迭代自蛇模型去噪算法（算法2）以及本文提出的自蛇模型和小波分析的集成去噪算法（算法3）的优劣，本文引入峰值信噪比(PSNR)和保护边缘指数(PEI)如下：

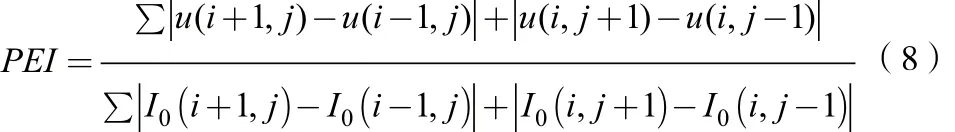
u为去噪后的图像，IO为原图像。峰值信噪比愈大，去噪后的图像噪声愈小。边缘保护指数大于1，图像噪声尚未处理干净；边缘保护指数小于1，图像已被过度滤波，图像比较模糊。边缘保护指数愈接近1，去噪后的图像边缘愈逼近原图像边缘，去噪后的图像愈清晰。所以，峰值信噪比愈高并且边缘保护指数愈接近1，处理后的图像噪声愈小、边缘愈清晰，去噪效果愈好。对Lena图像分别加不同方差高斯噪声，3种图像去噪算法峰值信噪比和保护边缘指数如表1所示。

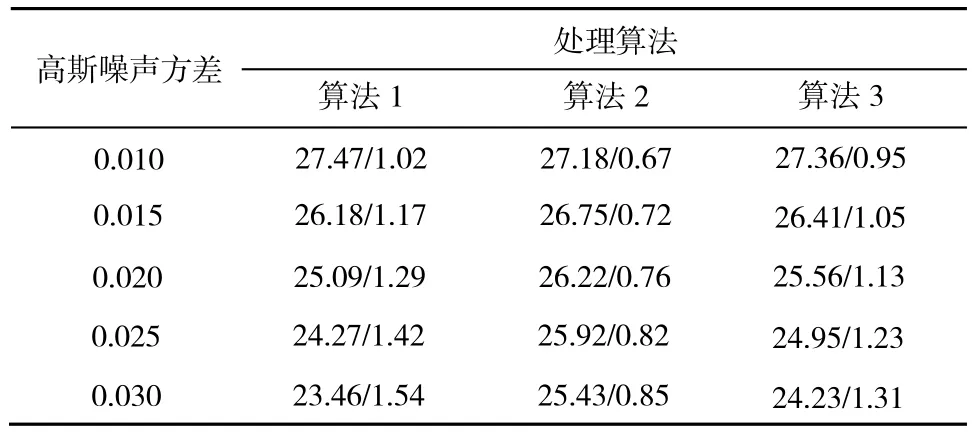
表1 3种算法图像去噪的峰值信噪比/保护边缘指数Tab.1 Comparison of PSNR and PEI by three methods

从表1数据知，在高斯噪声方差大于0.01时，算法3的峰值信噪比高于算法1，同时算法3的边缘保护指数更接近1，说明算法3的去噪能力好于算法1，并且算法3去噪后的图像更清晰。在高斯噪声方差大于0.01时，算法2的峰值信噪比均高于算法1和算法3，但是其边缘保护指数均小于1，说明算法2将图像的边缘和噪声同时去掉，虽然提高了图像的峰值信噪比，但是去噪后的图像较模糊。对于高斯噪声方差小于0.01时，算法1的峰值信噪比最高，去噪能力最强，但是算法3的边缘保护指数最接近小于1，图像最清晰。将Lena图像加入方差为0.015的高斯噪声，含噪图像及3种算法去噪图像如图2所示。

图2 Lena含噪图像及3种算法去噪图像Fig.2 Noisy image of Lena and results of denoising by three methods

图2（a）为含噪图像，图2（b）为算法1去噪图像，图2（c）为算法2去噪图像，图2（d）为算法3去噪图像，即本文算法去噪图像。从图2所知，本文提出的算法3噪声最小，边缘最清晰，与表1数据相符。

4 结 论

为了后续更高层次的图像处理, 有必要对含噪图像进行去噪。因为噪声和边缘同属于高频信息，在滤除噪声的同时也会模糊图像边缘, 图像质量得不到完美的改善。本文提出自蛇模型和小波分析的集成去噪算法，先对含噪图像进行自蛇模型滤波，去掉大部分噪声，再将其小波分解并保持低频分量不变，对高频分量再利用自蛇模型图像去噪，最后对对处理后的小波系数进行重构，得到对原信号的最佳恢复。实验结果表明，当噪声方差大于0.01时，本文算法在峰值信噪比和边缘保护指数两指标方面均好于自蛇模型算法（算法1）和2次迭代自蛇模型算法（算法2）；当噪声方差小于0.01时，本文算法处理后图像最清晰。

[1]Wei Zhang, Fei Yu, Hong-mi Guo.Improved Adaptive Wavelet Threshold for Image Denoising[C]//2009 Chinese Control and Decision Conference, 2009: 5958-5963.

[2]P L Shui, Z F Zhou, J X Li.Image denoising algorithm via best wavelet packet base using Wiener cost function [J].IET Image Processing, 2007,1(3): 311-318.

[3]Perona P, Malik J.Scale space and edge detection using anisotropic 0diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639.

[4]钱惠敏，茅耀斌，王执铨.基于各向异性扩散的几种平滑算法比较及改进[J].南京理工大学学报, 2007, 31(5):606-610.

Q IAN Hui-min, MAO Yao-bin, WANG Zhi-quan. Comparison and improvement of several smoothing algorithms based on anisotropic diffusion[J].Journal of Nanjing University of Science and Technology,2007, 31(5):606-610.

[5]郭茂银,田有先. 基于四阶偏微分方程的并行图像去噪算法[J].微电子学与计算机,2011,28(2):162-165.

GUO Mao-yin, TIAN You-xian. Parallel image denoising algorithm based on fourth-order partial differential equations[J].Microelectronics & Computer, 2011,28(2):162-165.

[6]王大凯,侯榆青,彭进业.图像处理的偏微分方程方法[M].北京:科学出版社, 2008.