永磁同步电机（PMSM）调速系统的智能控制算法研究

王宝忠 ，王 维 ，王 波

（1.江苏科技大学 电子信息学院，江苏 镇江 212003 ； 2.济宁供电公司 山东 济宁 272000）

在实际工业控制过程中经常会遇到滞后、时变、非线性的复杂系统，而PMSM调速系统就是一个复杂的非线性系统，无法获得精确的数学模型，单纯采用PI控制或模糊控制都不会取得较好的控制效果，而采用模糊自整定PI控制方式控制能充分发挥模糊控制鲁棒性强、动态响应好、上升时间快、超调小的优点，又具有PI控制器的动态跟踪能力和稳定精度高的特点。本文只对传统PI控制与模糊自整定PI控制的仿真结果进行比较。

1 模糊自整定PI控制器的设计

模糊自整定PI控制器就是运用模糊数学的基本理论和方法，把规则的条件、操作用模糊集表示，并把这些模糊控制规则及有关信息作为知识存入计算机知识库中，然后计算机根据控制系统的实际响应情况，运用模糊推理，就可以实现对PI参数的最佳调整[1]。模糊自整定PI控制器的结构如图1所示。

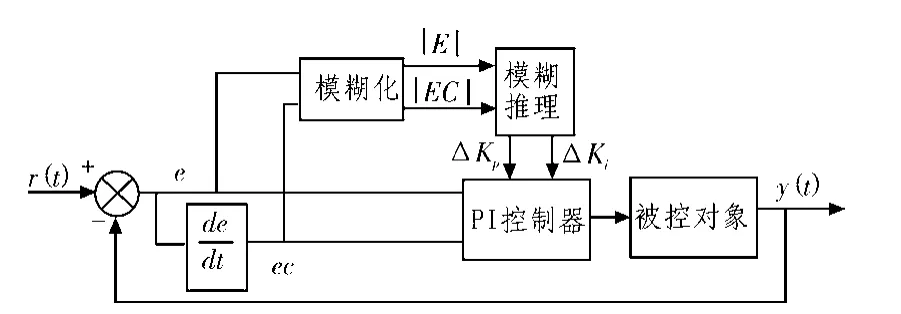
图1 模糊自整定PI控制器的结构Fig. 1 Structure of fuzzy self-tuning PI controller

PI参数模糊自整定控制器就是在常规PI调节器的基础上，应用模糊理论建立参数Kp、Ki与偏差绝对值|E|以及偏差变化绝对值|EC|间的二元连续函数关系的控制器[2]。

在实际控制系统中，误差的变化一般不是模糊论域中的元素，这就需要通过量化因子进行论域变换，定义误差的量化因子Ke=n/e，误差变化率量化因子Kec=n/ec，输出控制量量化因子Ku=u/n[3]。

本系统中，速度的给定值w*=500 r/m，系统的性能指标为：误差e的变化范围不大于给定值的3%，误差变化率ec的变化范围不大于误差的5%。那么，误差e的基本论域为[-15,15]，其量化因子Ke=6/15=0.4；误差变化率EC的基本论域为[-0.75,0.75]，其量化因子Kec=6/0.75=8。设参数△Kp、△Ki的调整范围不大于已整定参数的20%，系统已整定参数为Kp=2.4，Ki=7.2，则△Kp的基本论域为[-0.48,0.48]，其比例因子Kup=0.48/6=0.08；△Ki的基本论域为[-1.44, 1.44],其比例因子Kui=1.44/6=0.24。

在不同的|E|和|EC|下，被控过程对参数Kp、Ki的自整定要求如下。

1）当|E|较大，为使系统响应具有较好的快速跟踪能力，应取较大的Kp，同时为避免系统响应出现较大的超调，需对积分作用加以限制，通常取Ki=0。

2）当|E|为中等大小时，为使系统具有较小的超调，应取较小的Kp和适当的Ki，以保证系统的响应速度。

3）当|E|较小时，为使系统具有良好的稳态性能，应取较大的Kp和Ki。

总结工程设计人员的技术知识和实际操作经验，可得到针对△Kp、△Ki两个参数分别整定的模糊控制表。

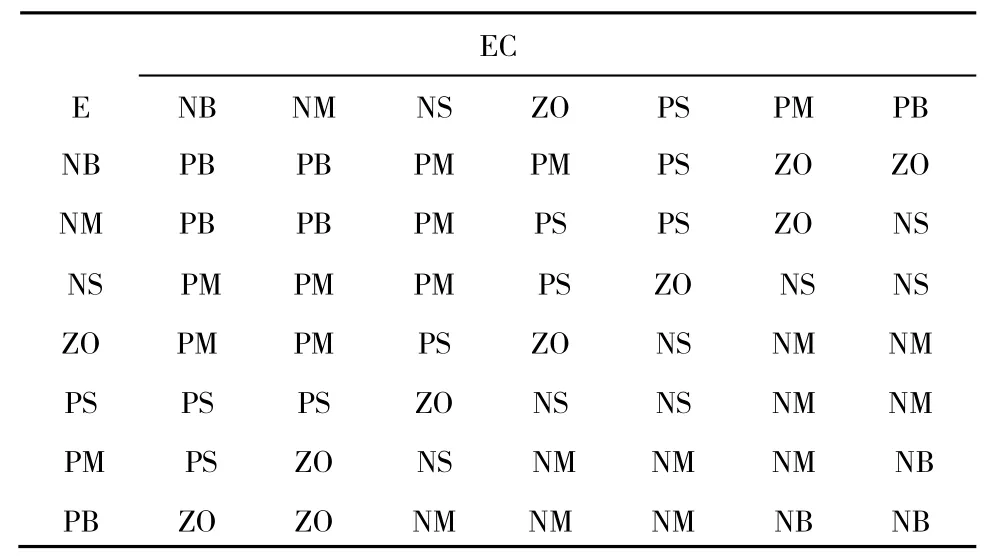
表1 △Kp的模糊规则表Tab.1 The fuzzy rule table of △ Kp

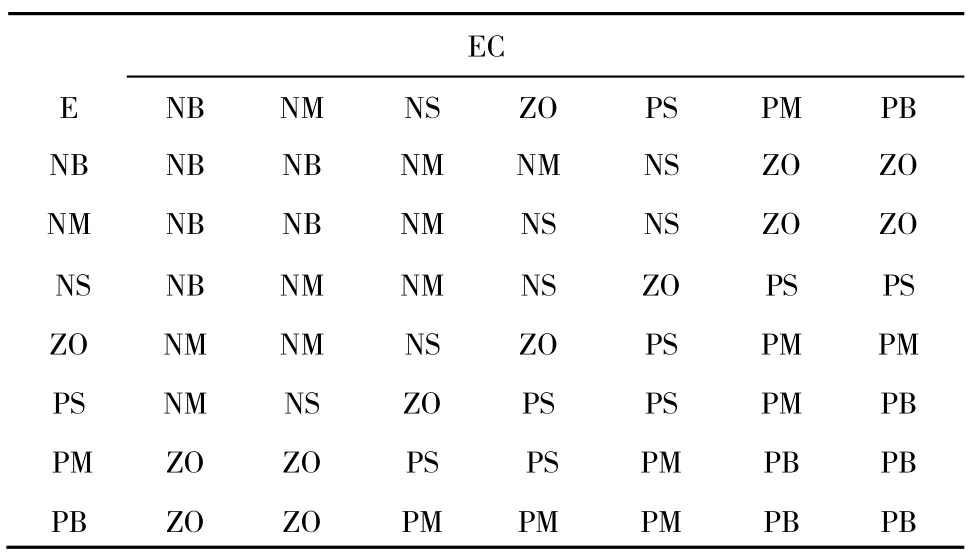
表2 △Ki的模糊规则表Tab.2 The fuzzy rule table of △ Ki

建立好控制规则表后，将系统误差和误差变化率范围定义为模糊集上的论域E,EC={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}，其模糊子集为E,EC={NB,NM,NS,ZO,PS,PM,PB}，为了计算机处理和实现方便，输入偏差E、偏差变化率EC和输出△Kp、△Ki的隶属函数均采用线性函数。根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计PI参数的模糊矩阵表，查出修正参数代入下式计算：

其中，K'P、K'i为常规PI控制器的设置参数；

△Kp、△Ki为模糊控制器输出的修正量；

Kp、Ki为模糊自整定PI控制器参数。

在线运行过程中，控制系统通过对模糊逻辑规则的结果处理、查表和运算，完成对PI参数的在线自调整。

2 模糊自整定PI控制器的仿真

启动MATLAB后，在主窗口中键入fuzzy回车，屏幕上就会出现 “FIS Editor”界面，即模糊推理系统编辑器。本文选择了如图2所示的模糊控制器，其中输入为偏差E和偏差变化率EC，输出为修正量△Kp、△Ki。该控制器为双输入双输出结构，其选用三角形隶属度函数和重心法解模糊的方式进行[4]。

接下来，按照表1和表2的模糊控制规则表编辑各个输出量与输入量之间的模糊控制规则，模糊控制规则编辑器的窗口[5]如图3所示。以if...then的形式输入49条模糊控制规则。

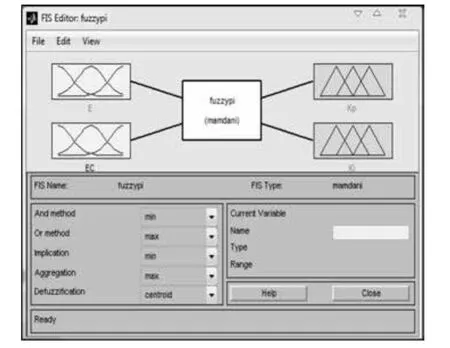
图2 模糊控制器结构图Fig. 2 Structure of fuzzy controller

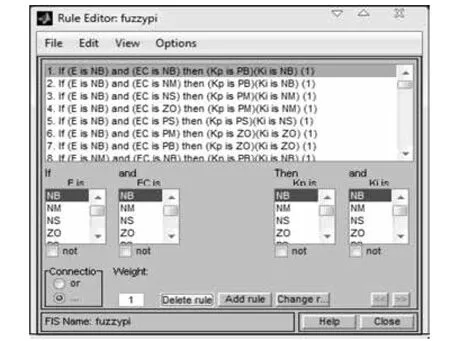
图3 模糊控制规则编辑器Fig. 3 Rule editor of fuzzy controller

最后可以生成输入输出的三维观察图形。Kp、Ki的三维曲面分别如图4、图5所示。

在确定量化因子和比例因子以及建立好模糊控制器之后，对图6的常规PI转速调节器进行优化，建立了图7所示的模糊自适应PI转速控制器，其中Kp、Ki的值保持不变。PMSM调速系统总仿真图[6]如图8所示。

3 仿真结果分析

在给定速度值为500 r/min时，常规PI调节器和模糊自整定PI调节器的仿真响应波形如图9、10所示。

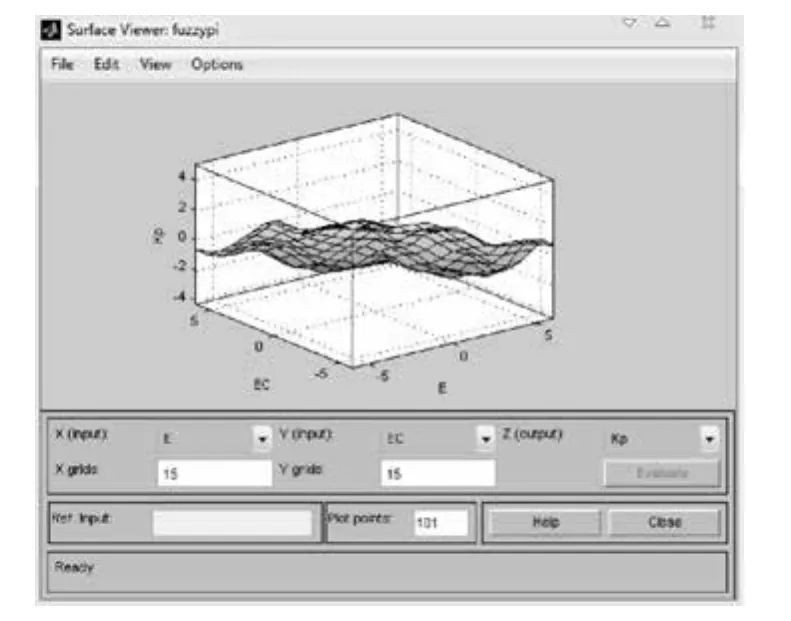
图4 Kp的输出三维图Fig. 4 3D output of Kp

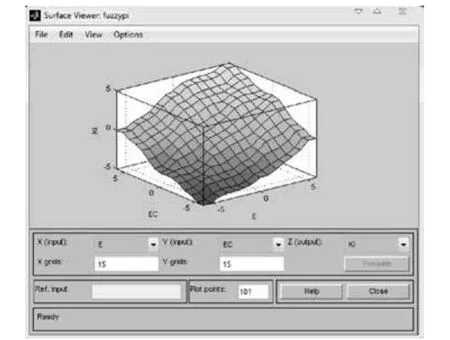
图5 Ki的输出三维图Fig. 5 3D output of Ki

仿真结果表明，采用常规PI控制器时，转速有一定的超调量，而且系统达到稳定的时间较长。采用改进后的模糊自整定PI控制器后，速度几乎没有超调，系统响应速度快。在系统运行时间t=0.2 s时加上5 N·m的额定负载，常规PI控制时，转速波动较大；而采用模糊自整定PI控制时，转速稍有下降，并很快恢复额定转速，具有较好的静差率。

图6 常规PI调节器Fig. 6 Conventional PI regulator

4 结束语

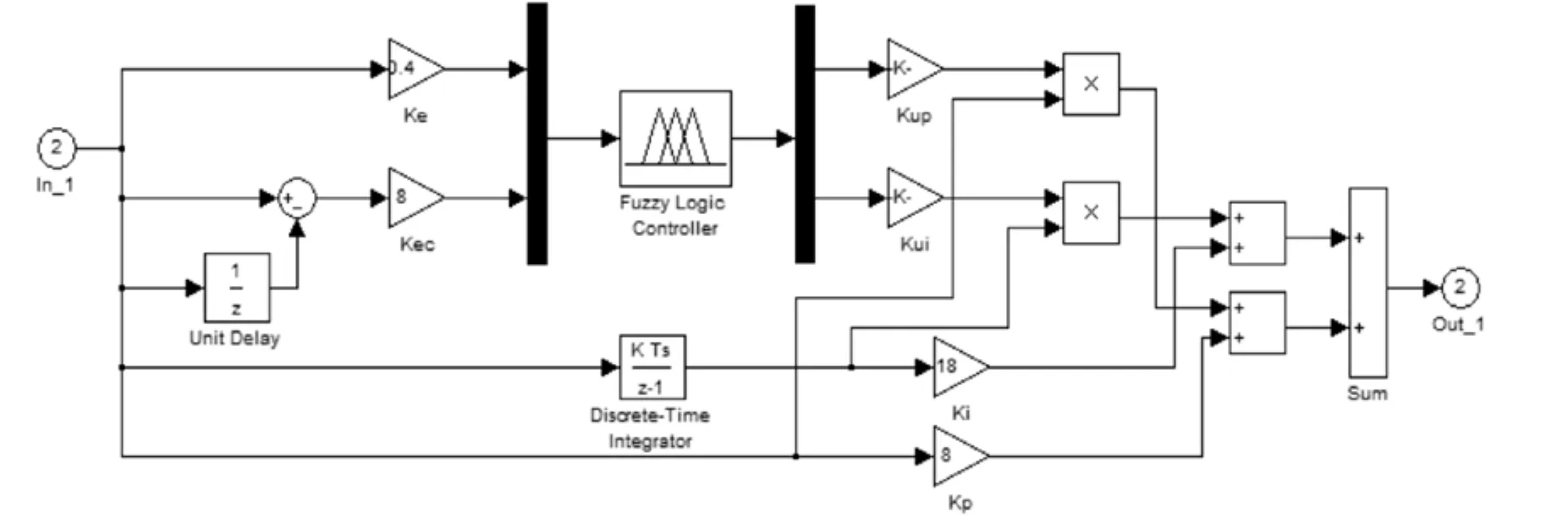
图7 模糊自整定PI调节器Fig. 7 Fuzzy self-tuning PI regulator

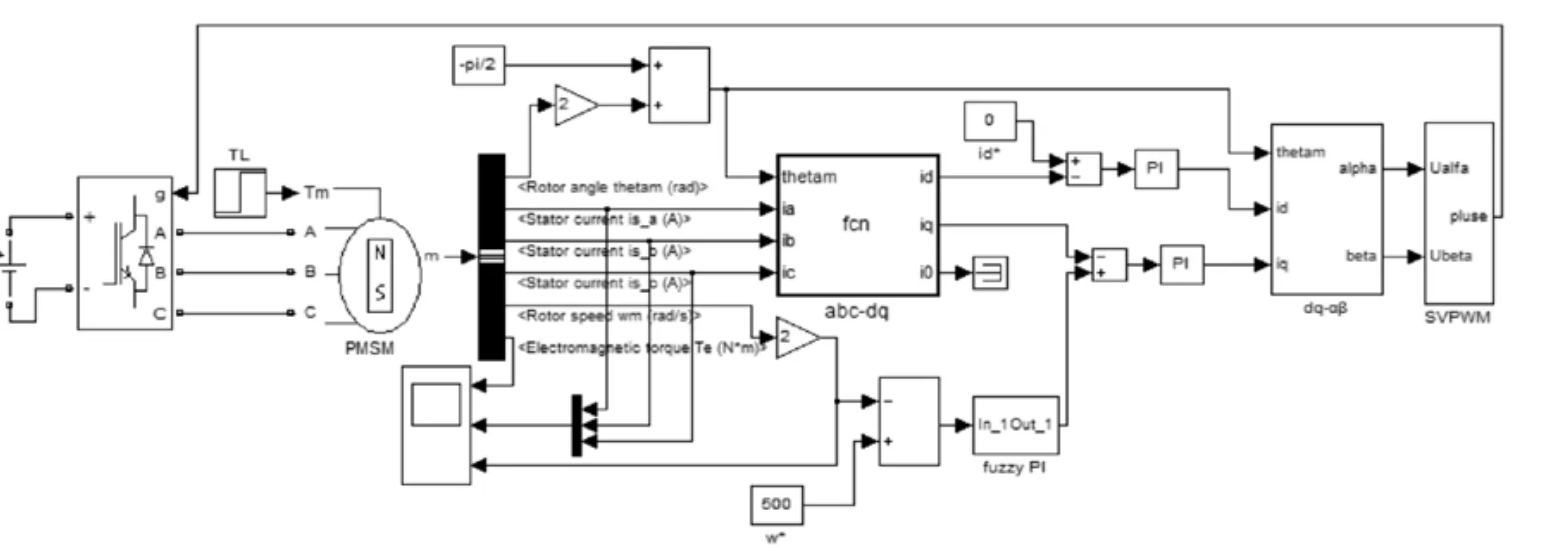
图8 PMSM调速系统模型Fig. 8 Model of PMSM speed control system

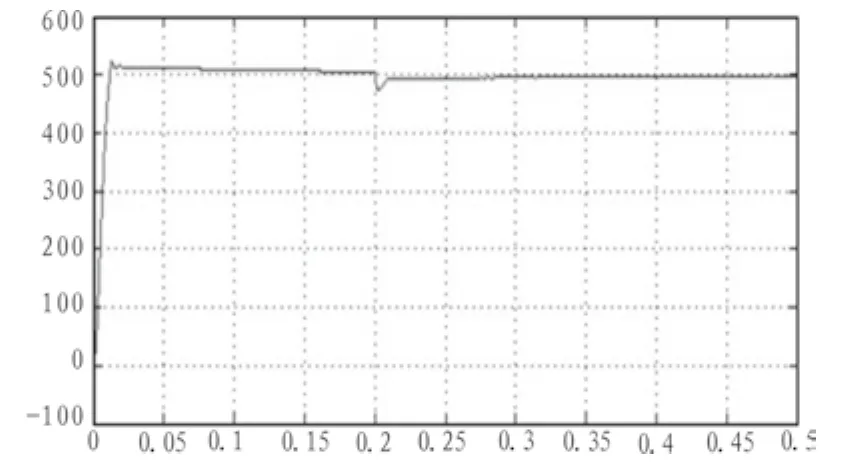
图9 常规PI仿真波形Fig. 9 Conventional PI simulation waveform

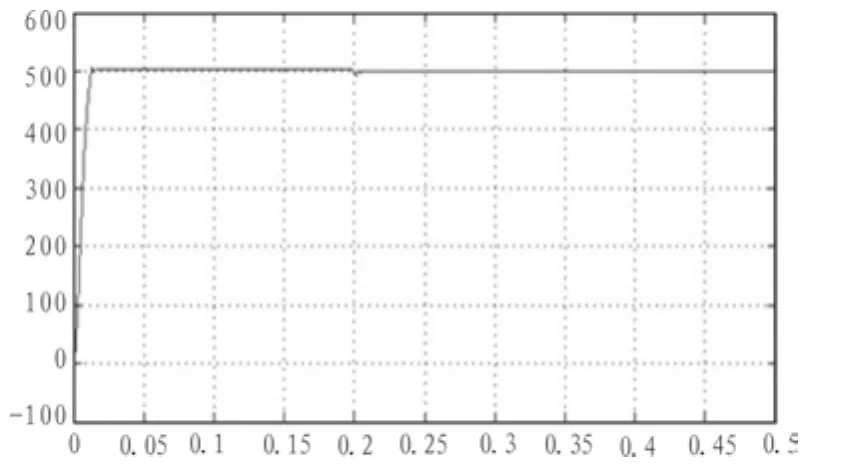
图10 模糊自整定PI仿真波形Fig. 10 Fuzzy self-tuning PI simulation waveform

本文分析了两种不同算法控制的PMSM[7-8]调速系统，并在MATLAB/simulink环境下实现了PMSM的基于常规PI和模糊自整定PI控制的建模和仿真，分别在空载和加负载两种情况下对系统进行仿真。仿真结果表明：基于模糊自整定PI控制的PMSM调速系统能够快速跟踪转速的变化，具有很好的控制特性。

[1]黄友锐,曲立国.PID控制器参数整定与实现[M].北京:科学出版社, 2010.

[2]曾光奇,胡均安,王东,刘春玲.模糊控制理论与工程应用[M].武汉:华中科技大学出版社, 2006.

[3]石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.

[4]刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社, 2004.

[5]周成. 模糊控制在永磁同步伺服系统中的应用与研究[D].长沙:湖南大学, 2009.

[6]姚绪梁.现代交流调速技术[M].哈尔滨:哈尔滨工程大学出版社, 2009.

[7]刘小河，王鹤华.基于SVPWM永磁同步电机反馈线性化控制[J].现代电子技术，2013(12):159-162.

LIU Xiao-he，WANG He-hua.Feedback linearization control of PMSM based on SVPWM[J].Modern Electronics Technique，2013(12):159-162.

[8]方国维，罗文广.基于神经网络补偿的永磁同步电机控制[J].电子科技，2013(4):143-145，149.

FANG Guo-wei，LUO Wen-guang.PMSM control based on neural network compensation[J]. Electronic Science and Technology，2013(4):143-145,149.