基于小波变换的角点检测算法

孙青锋

（安徽机电职业技术学院电气工程系，安徽芜湖 241002）

角点是图像的一个重要的局部特征，包含有丰富的信息。目前，对于角点的定义，有很多说法，普遍来说，其立足点基本上都放在二维图像亮度变化剧烈的点以及图像边缘曲线上曲率极大值的点这两个方面。角点在保留图像重要特征的同时，具有旋转不变性，几乎不受光照条件的影响，可以有效地减少信息的数据量，有效地提高了计算的速度，有利于图像的可靠匹配，使得实时处理成为可能。其在三维场景重建、运动估计、目标跟踪、目标识别、图像配准与匹配等计算机视觉领域起着非常重要的作用。

1 Harris角点检测算法

Harris角点检测法[2]是由Harris和Stephens提出来的。经典Harris角点检测法的基本理论基于Moravec算子，其引入了自相关函数理论，结合角点检测与图像的局部自相关函数，通过特征值分析来判断待检测点是否为角点。

在原始的Harris角点检测算法中，使用的角点响应函数为

上式中的Det为对称矩阵M两个特征值的乘积，Tr为特征值的和，K是常数因子，介于0.03至0.15之间。

其中，Ix、Iy分别表示图像沿X和Y方向上的梯度。

只有R值大于选定门限，并且在八个相邻的方向上为局部极大值时，这个点才可被认为是角点。在使用经典的Harris角点检测法时，K的选取常带来一些不必要的误差，在后续的改进中，一般不用该响应函数。

Harris算子的角点检测法，是目前效果较好的图像特征点提取算法，当图像存在旋转、视点变化或灰度变化时，角点提取效果依然良好。但是，它对噪声比较敏感，在噪声的干扰下容易提取大量的伪角点。另外，传统的Harris角点检测算子不具有尺度不变性，在不同图像分辨率下，角点容易产生漂移。

2 基于小波变换角点检测方法

2.1 小波变换

小波分析理论起源于20世纪初，由Haar首先提出了Haar小波规范正交基概念。随后，Mallat建立快速小波变换方法[3]，实现小波分析从数学表达到技术应用的转变。在Daubechies、Swelden等人推动下，小波变换迅速发展，应用越来越广泛。

如图1所示，在小波分解的每一层，生成4幅大小为原图像四分之一的新图像。这些新图像分别为：保留原图像的低频信息部分和其他三个方向（水平、垂直、对角）的高频信息部分，其中，高频部分在小波变换下，可近似为不同方向的偏导数。在图像的小波分解中，仅用低频部分来产生下一级分解。

图1 图像的小波分解

2.2 基于小波变换的角点检测

考虑到传统Harris角点检测算子在抗噪方面的不足，结合小波变换的多尺度特性，提出一种基于小波变换的角点检测算子，其步骤如下：

1）对图像应用平稳小波变换分解，在每个分解层上，将得到四个系列系数，分别为近似系数与其他三个方向的高频系数；

2）以小波分解得到的水平方向(Ix)、垂直方向(Iy)、对角方向(Ixy)高频系数构建一个自相关矩阵；

3）采用改进的Harris角点响应函数进行特征点提取。

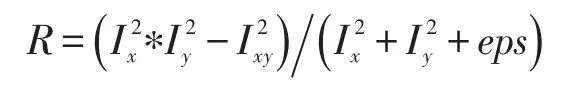
3 实验结果

本文实验结果在MATLAB7.8下仿真得出。选用Lena图像作为实验图像，大小为256*256，在不加噪声和加噪声两种情况下用本文算法进行实验，并与传统Harris角点检测算法进行对比分析。

图2 原始图像

图3 传统Harris角点检测

图4本文算法

图2左边为Lena图像，右边为叠加了高斯白噪声δ=0.01的Lena图像，图3为传统Harris角点检测算法分别在图2的两种情况下得到的角点，可以看出，传统的Harris角点检测算法检测到的角点较多，但其对噪声敏感。另外，在实际仿真中，由于其计算量相对较大，用时在0.5秒左右。图4为本文算法在图2情况下的应用，在两幅图像中，加噪声前后得到的角点数基本相当，并且其角点定位基本一致，稳定性良好，另外，其提取角点的时间在0.2秒左右。基于本文角点检测算法，在后续图像配准的应用中，具有较好的匹配效果。

4 总结

小波变换的多尺度特性，在大尺度下能够得到图像概貌特征，有利于抑制噪声，小尺度下可以得到图像的细节部分，便于精确定位角点。基于这种优点，提出一种结合小波变换的角点检测算法，平衡了噪声和定位不易兼得的矛盾，角点检测效果较理想。但是，小波的选择和阈值等一些参数的设置，将关系到最终的检测结果，下一步，应该在自适应方面深入研究，以便对算法加以改进。

[1]schimid C，mohr R，bauckhage C.Evaluation of interest point detecters[J].International Journal of Computer Vision，2000，37(2)：151-172.

[2]harris C,stephens M J.A combined corner and edge detect⁃er[A].In 4th Alvey Vision Conference，1988：147-152.

[3]Mallat.S G A theory for multi-resolution signal decomposi⁃tion：the wavelet representation[J].IEEE Transactions on Pat⁃tern Analysis and Machine Intelligence，1989，11：673-694.

[4]Rafael C Gobzalez，Richard E Woods.Digital Image Pro⁃cessing[M].Second Edition，Bei Jing：Publishing House of Elec⁃tronics Industry，2007.

[5]zitova B，flusser J.Image registration methods：a survey[J].Image and Vision Computing，2003，21：977-1000.

[6]Stephane Mallat，Wen Liang Huang.Singularity detection and processing with wavelets[J].IEEE Transactions on Informa⁃tion Theory，1992，38(2)：617-643.

[7]Herbert Bay，Tinne Tuytelaars，Luc Van Gool.Speed up ro⁃bust features[J].Computer Vision and Image Understanding，2008，110(3)：346-359.