120 km/h地铁减振垫浮置板动力学特性分析及减振垫刚度取值研究

杨文茂

(中国中铁二院工程集团有限责任公司，成都 610031)

120 km/h地铁减振垫浮置板动力学特性分析及减振垫刚度取值研究

杨文茂

(中国中铁二院工程集团有限责任公司，成都 610031)

目前，国内部分地铁设计速度已达120 km/h，有必要针对该速度条件下的减振垫浮置板动力特性以及减振垫刚度取值等问题展开专门研究。基于有限元软件，建立车辆-轨道-隧道耦合动力学模型，可对120 km/h速度条件下地铁车辆、钢轨、减振垫浮置板，以及隧道结构等细部结构的动力学特性进行详细的研究。经计算和检算可知，在减振垫浮置板上运行120 km/h速度的地铁A型车，其各项动力学指标均满足动力学检算标准；同时计算结果表明，减振垫面刚度宜取0.01～0.02 N/mm3.

地铁；减振垫浮置板；减振垫刚度；动力学

1 研究背景

目前，国内部分地铁的设计最高行车速度已达120 km/h，如上海地铁16号线，以及在建的深圳地铁11号线等。与以往的地铁速度80～100 km/h相比，在这种较高的速度条件下，减振垫浮置板的动力学特性存在着很大的特殊性，相应的减振垫刚度等关键设计参数的取值也需重新进行分析和论证。

减振垫刚度一般用面刚度来表示，面刚度的合理取值是减振垫浮置板设计中的核心问题。面刚度过大会降低减振效果，面刚度过小则会造成动位移超限，影响结构的安全性和稳定性。目前，市场上减振垫的形式多种多样，其面刚度也存在着较大差异，如何合理地选择减振垫面刚度，以满足较高行车速度条件下减振垫浮置板的设计要求，是一个亟待研究的问题。

在已有的研究[1-9]基础上进行进一步研究，采用商业有限元软件建立了地铁车辆-轨道-隧道耦合动力学模型，该模型的主要特点是：结构详尽，充分考虑了地铁车辆、钢轨、扣件、浮置板、减振垫、基底、隧道等结构组成，可以更详细地对各细部结构进行计算和检算；且采用实体单元模拟钢轨、道床和隧道结构，因此可以模拟出各部分的高频振动，对于振动加速度等动力响应计算结果模拟的更准确、更加符合实际情况。

采用上述地铁车辆-轨道-隧道耦合动力学模型，对不同减振垫面刚度条件下的动位移和减振效果进行了计算分析与比较，对面刚度的合理取值范围提出了建议。

2 车辆-轨道-隧道耦合动力学模型

基于商业有限元软件建立地铁车辆-轨道-隧道耦合动力学模型，主要考虑地铁A型车(包括车体、转向架、轮对、一系悬挂和二系悬挂等)、轨道结构(包括钢轨、扣件和减振垫浮置板道床)和隧道结构(包括隧道支护、隧道外的一部分土体等)3部分。

2.1 地铁车辆

地铁车辆为多刚体模型，由车体、转向架、轮对、一系悬挂(轴箱悬挂)和二系悬挂(中央悬挂)等部分组成。地铁车辆的整体模型如图1所示。车体参数参照地铁A型车辆取值，车速取120 km/h。

图1 地铁车辆模型

2.2 钢轨和扣件

钢轨选用实体单元进行模拟，按实际截面属性建模，考虑钢轨的截面积、惯性矩以及扭转弯矩等参数，可以全面考虑钢轨的纵、横、垂向位移及转角。

扣件采用弹簧单元进行模拟，可以全面考虑扣件的纵向阻力、横向刚度和垂向刚度。扣件参数取值参照目前地铁上较为常用的DT-Ⅲ系列扣件(垂向刚度30 kN/mm)，扣件间距取600 mm。

2.3 减振垫浮置板道床

图2 减振垫浮置板实体单元模型

减振垫浮置板道床主要由浮置板、减振垫、道床基底3部分构成，均采用实体单元进行模拟，可以全面考虑结构的几何尺寸和物理属性，如图2所示。浮置板结构尺寸为：长4 170 mm，宽2 400 mm，厚240 mm(含40 mm调整层)；减振垫层厚30 mm；道床基底厚120 mm。轨道结构高度为640 mm。

2.4 隧道结构模型

采用矩形隧道，隧道结构采用实体单元进行模拟。为尽量减小边界效应的影响，隧道外考虑100 m×100 m范围内的土体。土体简化为弹性体结构。

2.5 轮轨接触和轨道不平顺

轮轨法向力由赫兹非线性弹性接触理论确定，轮轨切向力由蠕滑理论确定[10]；轨道不平顺采用美国5级轨道谱[11-12]。

2.6 车辆-轨道-隧道耦合动力学模型的建立

采用以上方法建立的车辆-轨道-隧道耦合动力学模型如图3所示。

图3 车辆-轨道-隧道耦合动力学模型

3 动力学计算结果汇总

采用本文所建立耦合动力学模型，对多种面刚度条件下的减振垫浮置板的动力学特性均进行了仿真分析。下面以其中一种工况(减振垫面刚度取0.02 N/mm3)为例，简要介绍计算结果。

3.1 车辆运行平稳性指标计算结果

计算得到的车体振动加速度时程曲线如图4所示。其中，车体振动加速度最大值为0.021g。

图4 车体振动加速度时程曲线

根据《铁道车辆动力学性能评定和试验鉴定规范(GB5599—85)》[13]，客车运行平稳性按车体平均最大振动加速度评定。车体平均最大振动加速度应符合

3.2 钢轨动力学计算结果

计算得到的钢轨动位移和钢轨加速度的时程曲线分别如图5、图6所示。钢轨动位移最大值为2.477 mm，钢轨振动加速度峰值为23.764g。

图5 钢轨动位移时程曲线

图6 钢轨振动加速度时程曲线

根据《浮置板轨道技术规范》(CJJ-T 191-2012)[14]，钢轨垂向位移不应大于4 mm。本文计算得到的钢轨位移最大值为2.477 mm，满足要求。目前国内对于地铁钢轨振动加速度限值尚无明确规定，但根据多地地铁实测的结果，钢轨加速度峰值一般为几十倍重力加速度，与计算结果亦相吻合。

3.3 浮置板振动的动力学计算结果

计算得到的浮置板振动加速度时程曲线如图7所示，轨道板的振动加速度峰值为1.090g。

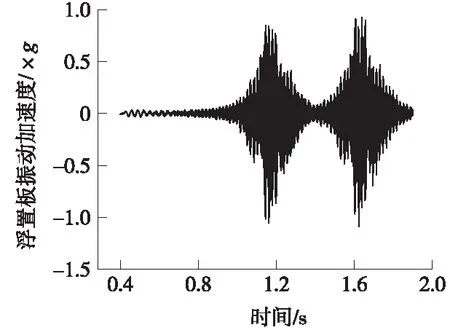
图7 浮置板振动加速度时程曲线

根据《浮置板轨道技术规范》(CJJ-T 191-2012)，可采用4～200 Hz范围内的1/3倍频程振动加速度Z振级，作为振动的评价量，具体的计算方法为

式中，VLz为Z振级；VLz(i)为1/3倍频程频谱序列中，第i个中心频率所对应的分频振级。

对浮置板振动加速度时域序列进行1/3倍频程变换，即得到浮置板分频振级的频域序列。其中，4～200 Hz内的分频振级如图8所示。利用式(2)对该频率范围内的分频振级进行叠加，即得到浮置板振动加速度Z振级为88.049 dB。

图8 浮置板振动加速度分频振级曲线

3.4 隧道壁振动的动力学计算结果

计算得到的隧道壁的振动加速度时程曲线如图9所示，隧道壁的振动加速度峰值为0.006g。

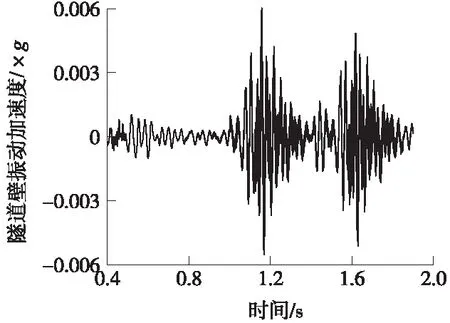
图9 隧道壁振动加速度时程曲线

对隧道壁振动加速度时域序列进行1/3倍频程变换，即得到隧道壁分频振级的频域序列，其中4～200 Hz内的分频振级如图10所示。利用式(2)对该频率范围内的分频振级进行叠加，即得到隧道壁振动加速度Z振级为59.050 dB。

图10 隧道壁振动加速度分频振级曲线

4 不同面支承刚度对比分析

目前，国内地铁所采用减振垫一般为橡胶、聚氨酯等材料，可通过改变垫子厚度、调整材料配方等方式以实现面支承刚度的调整。调整范围一般为0.01 ～0.04 N/mm3，较为常用的取值有0.01 N/mm3、0.02 N/mm3、0.04 N/mm33种。下面针对这3种刚度取值，分别进行钢轨动位移、浮置板动位移、减振效果3项控制性指标的分析和对比。

4.1 不同面支承刚度下的动位移对比分析

利用本文所建立的耦合动力学模型，计算得到0.01 N/mm3、0.02 N/mm3、0.04 N/mm33种面支承刚度条件下的钢轨、浮置板动位移汇总如表1所示；钢轨、浮置板动位移的时程图曲线分别如图11、图12所示。

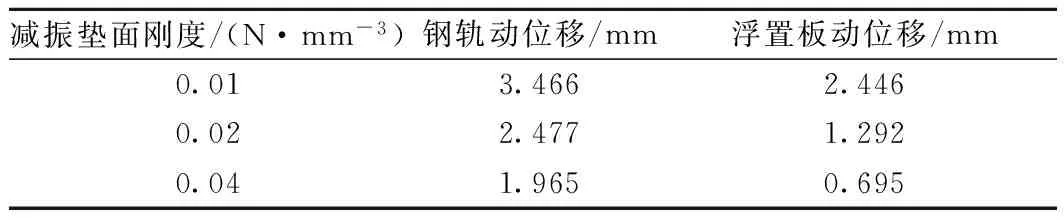
表1 不同面刚度下的动位移汇总

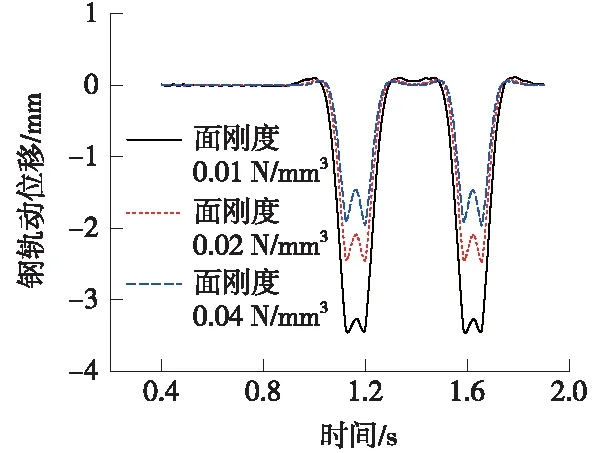
图11 不同面刚度下的钢轨动位移时程曲线

图12 不同面刚度下的浮置板动位移时程曲线

从表1中的计算结果可以看出，减振垫面刚度越小，动位移越大。当面刚度取0.01N/mm3时，钢轨动位移和浮置板动位移最大，分别为3.466 mm、2.446 mm。

根据《浮置板轨道技术规范》(CJJ-T 191-2012)，浮置板轨道在列车额定荷载作用下钢轨的最大垂向位移不应大于4 mm，浮置板的最大垂向位移不应大于3 mm。当浮置板面支承刚度在0.01 ～0.04N/mm3内取值时，钢轨和浮置板的动位移均满足规范要求。

4.2 不同面支承刚度下的减振效果对比分析

利用本文所建立的耦合动力学模型，可计算得到0.01 N/mm3、0.02 N/mm3、0.04 N/mm33种面刚度条件下的浮置板道床，以及普通整体道床的隧道壁垂向加速度振级，然后用浮置板的隧道壁振级减去普通道床的隧道壁振级，即得到浮置板的减振效果，如表2所示。各种面刚度下的隧道壁垂向加速度1/3倍频程分频振级如图13所示。

表2 不同面支承刚度下的减振效果汇总

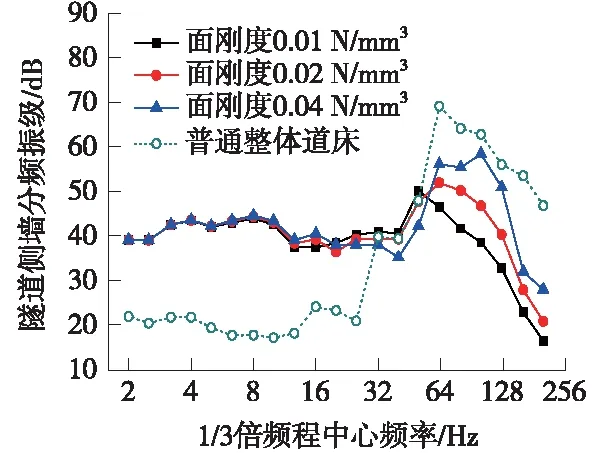
图13 不同面刚度下的隧道壁加速度1/3倍频程曲线图

从表2可以看出，浮置板面支承刚度越小，其减振效果越好。在具体的地铁减振设计中，基于经济性等多方面的综合考虑，一般要求浮置板道床的减振效果不小于10 dB。表2中，当面刚度取值为0.04 N/mm3时，减振效果仅为8.060 dB，故在地铁设计中应尽量避免这种刚度取值。当面刚度取值范围为0.01～0.02 N/mm3时，减振效果可达12 dB以上，能较好地满足10 dB以上的减振需求并留有一定的减振能力富余度。故减振垫面刚度取值宜为0.01～0.02 N/mm3。

5 结论和建议

(1)本文所建立的地铁车辆-轨道-隧道耦合动力学模型，充分考虑了地铁车辆、钢轨、扣件、浮置板、减振垫、道床基底、隧道及其周围土体的组成，可以更详细地对各细部结构进行计算和检算。

(2)基于最新颁布实施的《浮置板轨道技术规范》(CJJ-T 191-2012)进行动位移和减振效果的检算，结果更为科学和规范。以往的地铁动力学检算缺乏统一的规范作为依据，导致评价体系混乱，难以形成统一的标准。以减振效果的评价为例，有的以插入损失作为评价指标，有的以加速度级作为评价指标，相应的研究成果难以进行横向对比和分析。根据最新颁布实施的浮置板技术规范，以4～200 Hz范围内的1/3倍频程

振动加速度Z振级作为评价指标，更为科学和规范。以后的地铁动力学检算也应严格按照该规范执行，逐渐在业内形成一个统一的地铁动力学检算和评价体系。

(3)经计算和检算可知，在铺设减振垫浮置板的隧道内运行速度120 km/h的地铁A型车，其车辆平稳性指标、钢轨、浮置板和隧道结构的动力学计算结果均满足动力学检算标准。

(4)从满足减振要求同时兼顾安全的角度出发，建议减振垫面刚度取值范围宜为0.01～0.02 N/mm3，这样一方面能达到10 dB以上的减振效果，并留有一定的减振能力富余量，同时不会引起轨道结构的动位移超限。

[1] 刘锦辉，周华龙，陈冶.隔离式减振垫浮置板道床施工工艺的探讨[J].环境工程，2012 (S1)：84-88．

[2] 周华龙.深圳地铁2号线轨道减振降噪技术的应用[J].地下工程与隧道，2011(4)：7-11．

[3] 高亮，杨文茂，曲村，蔡小培.高铁长大桥梁CRTSⅠ型板式无砟轨道无缝线路的动力学特性[J].北京交通大学学报，2013 (1)：73-79．

[4] 王平，刘学毅，李成辉.连续支承条件下轨道位移波的动力特性分析[J].西南交通大学学报，2001(1)：17-22．

[5] 刘作为.减振垫浮置板轨道的振动及隔振效果研究[D].北京：北京交通大学，2012．

[6] 刘峰，曾向荣，张宏亮，李文英.新型橡胶减振垫浮置板的应用研究[J].都市快轨交通，2013(3)：50-53．

[7] 杨文茂.重载铁路隧道内无砟轨道结构选型研究[D].北京：北京交通大学，2012．

[8] 毛东兴，张晓洁.城市轨道交通浮置式减振措施的减振降噪效果[J].环境工程，2012(S1)：47-52.

[9] 邹策，袁昊，时光明.新型高弹性减振垫在北京地铁的研发与应用[J].铁道标准设计，2009(2)：13-16．

[10] 翟婉明.车辆-轨道耦合动力学[M].3版.北京：科学出版社，2007:44.

[11] 陈果，翟婉明.铁路轨道不平顺随机过程的数值模拟[J].西南交通大学学报，1999，34(2):138-142．

[12] 王开云，翟婉明，蔡成标.左右轨道不平顺功率谱转换中心线功率谱的方法[J].交通运输工程学报，2002，2(3)：27-29．

[13] 中华人民共和国住房和城乡建设部.CJJ/T 191—2012 浮置板轨道技术规范[S].北京：中国建筑工业出版社，2013．

[14] 国家标准局.GB 5599—85 铁道车辆动力学性能评定和试验鉴定规范[S].北京：中国标准出版社，1986．

Research on Dynamic Characteristics of Metro Damping Pad Floating Slab and Selection of Damping Pad Stiffness at 120 km/h

Yang Wenmao

(China Railway ErYuan Engineering Group Co.， Ltd.， Chengdu 610031， China)

As designed metro speed has reached 120 km/h， it is necessary to conduct a research on the characteristics of the damping pad floating slab and selection of damping pad stiffness. Based on FEM software， a vehicle-track-tunnel coupled dynamic model is established to study the dynamic characteristics of metro vehicle， rail， floating slab track and tunnel under the action of 120 km/h train speed. The results of calculation and verification show that when type A vehicle of 120 km/h runs on damping pad floating slab track， various dynamic indexes of the vehicle meet the dynamic verification standards. Meanwhile， the calculation results demonstrate that the stiffness of damping pad should be 0.01～0.02 N/mm3．

Metro; dynamics; Damping pad floating slab; Damping pad stiffness; Dynamics

2014-02-21；

：2014-03-24

杨文茂(1988—)，男，助理工程师，2012年毕业于北京交通大学道路与铁道工程专业，工学硕士，E-mail：350538308@qq.com。

1004-2954(2014)11-0028-04

U213.2+4

：A

10.13238/j.issn.1004-2954.2014.11.007