基于超稳定理论的自适应控制在单相有源滤波器中的应用

徐长波，鲁 伟，李春文

（清华大学 自动化系，北京 100084）

0 引言

伴随着电力电子装置的广泛应用，电能质量的问题日益严重，特别是谐波污染，给电网的安全性提出了挑战。目前治理谐波问题主要通过无源滤波器PF（Power Filter）和有源滤波器 APF（Active Power Filter）[1-4]。基于谐振原理的无源滤波器经济性较好，但是只能消除特定次数的谐波且容易与电网产生谐振[5]。APF大多采用与负载并联在电路中产生与负载谐波反相的电流来抵消电网中电流的畸变[6]。为了有效地补偿非线性负载的谐波电流，有效的控制策略就显得尤为重要。

目前应用于APF中的控制方法很多，如PI控制、广义积分、单周控制和预测控制等[7-11]，但是动态效果或者鲁棒特性不能满足APF的需求。针对APF要求系统有快速响应、耗损少且抗干扰能力强等性能，一些传统的算法不能满足需要。模型参考自适应控制 MRAC（Model Reference Adaptive Control）属于参数自适应控制系统的一种，因具有适应性和鲁棒性等优点而应用于多种场合，特别是航空航天，在APF中的应用还较少见。文献[12-15]采用李雅普诺夫稳定性理论设计了模型参考自适应控制器，但是这种方法的成功与否和选择的李雅普诺夫函数有很大关系，而且有些系统可供选择的李雅普诺夫函数唯一，因此这种方法受到了限制。采用波波夫超稳定性设计模型参考自适应控制器时，可以得到更一般的适应律，更容易设计[16]。

本文以单相并联APF为研究对象，首先引入了单相APF的结构数学模型，通过线性化的方法得到单相APF的近似线性模型；再利用波波夫稳定性理论设计自适应模型跟随控制器；最后给出了仿真结果，验证所提控制策略的有效性。

1 单相并联APF的结构及原理

单相并联APF的电路结构主要是由直流侧电容、逆变器、输出滤波电感组成，如图1所示。其中us为电源电压；udc为直流侧电容两端的电压，is为系统电流，iL为负载电流，ic为逆变器的输出电流，L为滤波电感，C为直流侧电容，idc为流过直流侧电容的电流，VT1—VT4为开关器件。通过一定的检测和控制算法合理控制开关器件的开断，实现APF输出的电流跟踪指令电流信号，进而使电网侧的电流为期望的正弦波。

图1 单相并联APF的电路结构Fig.1 Structure of single-phase shunt APF

2 单相并联APF的建模

由图1电路拓扑结构，根据基尔霍夫电压定律，可得：

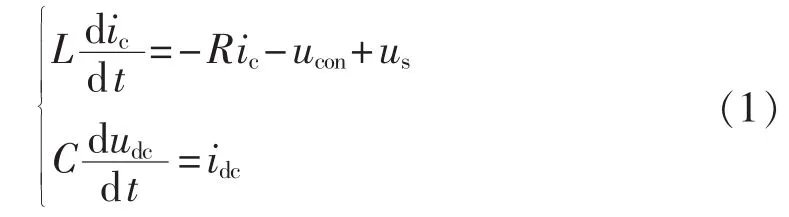
令S为开关函数，若开关器件采用双极性PWM方式进行控制时，S取值如下：

则有：

将式（3）代入式（1）整理可得：

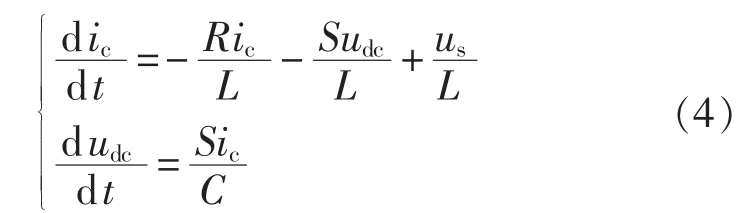
根据式（4），可以建立单相并联APF的数学模型如下：

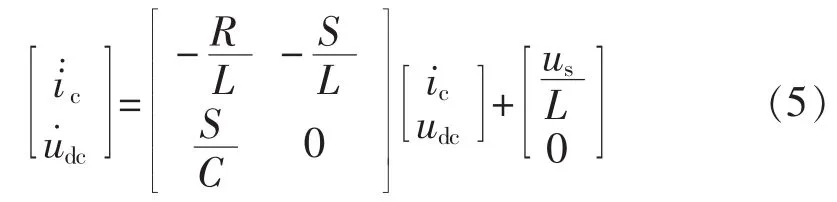
显然，系统模型既包含了连续动态又包含了离散动态，是一个混杂动态系统。为了便于处理，采用周期平均方法[17]对该模型进行简化。假定直流侧电容电压经过PI控制能够稳定在给定值Udc，令：

其中，Ts表示PWM周期。经过周期平均以后，单相并联APF的状态空间模型可以简化为线性模型：

利用文献[14]中的线性化方法得到系统式（8）的近似线性模型。 取 d=d0，d0ϵ[0，1]，且为常数。 令x0为系统式（8）的平衡点，即满足：

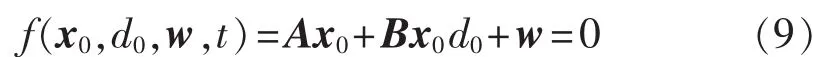
则有：

对其进行泰勒展开并忽略其高次项可得：

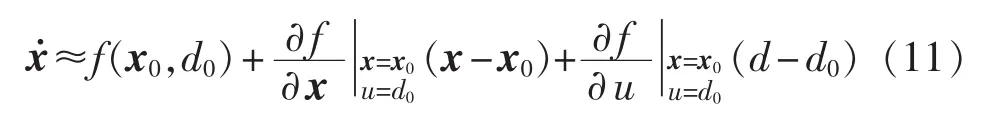
定义：

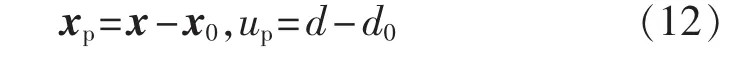
可得：

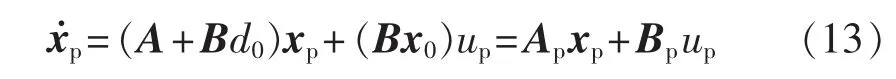
3 单相并联APF自适应控制器的设计

由于APF系统本身和环境干扰存在不确定性，当滤波参数明显变化时，常规PI控制的效果不尽如人意，甚至导致系统的不稳定。利用超稳定性理论设计模型跟随自适应控制系统为非线性控制，当系统参数发生变化时，实时修正调整，驱动系统跟踪参考模型状态，可以提高APF系统的补偿效果。图2为应用超稳定理论设计的模型跟随系统控制框图。

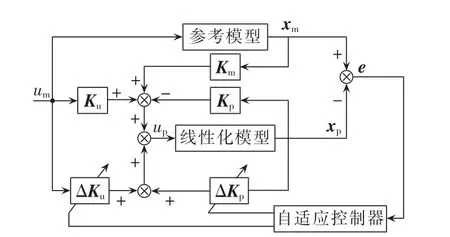
图2 单相并联APF的系统控制框图Fig.2 Block diagram of single-phase shunt APF control

设其参考状态模型方程为：

其中，umϵR 为参考输入；xmϵR2×1是参考模型的状态向量；AmϵR2×2、BmϵR2×1为参考模型系统矩阵。

定义状态误差为：

控制器的设计目的是要求控制APF的输出跟踪参考谐波信号，使误差e接近0，即。 根据文献[18]可以定义自适应控制器的输出为：

其中，Kp、Km、Ku为如图2中适当维数控制系数的增益矩阵。

但是在实际运行中，Ap和Bp为动态系数矩阵，而且这种变化是未知且不能测量的，但是控制器系数的增益矩阵是依赖Ap和Bp的值，因此在增益矩阵Kp和Ku中加入可调部分来抑制系统参数的动态变化，以保证可以完全地模型跟随，则控制律如下所示：

假设系统满足完全跟踪的充分条件式（18），并需要适应速度比参数漂移速度快。

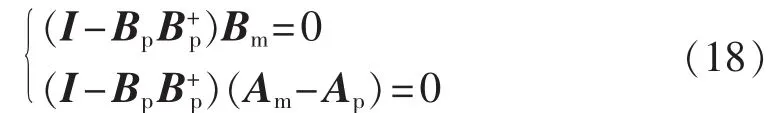
其中，B+p表示 Bp的伪逆矩阵，B+p=（BTpBp）-1BTp。

则误差的状态方程为：

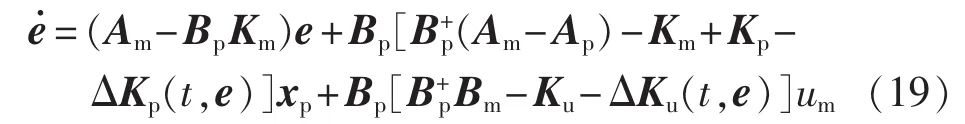
先将系统等价为非线性时变反馈系统，其前向环节为：

非线性时变的反馈环节为：

为了使系统式（20）是渐近稳定的，根据超稳定性理论，需要满足波波夫积分不等式，即

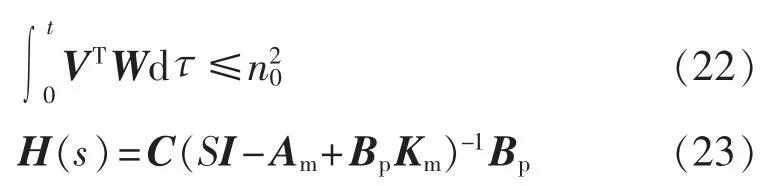
是严格正实的（其中n0为不依赖于时间的有限正常数）。但是由于Ap和Bp是未知定常矩阵，所以在控制器的设计中取其标称值为A0p和B0p。具体的设计步骤如下。

a.确定参考模型参数。参考模型根据文献[15]得到参考模型的2个极点，可以得到系统矩阵：

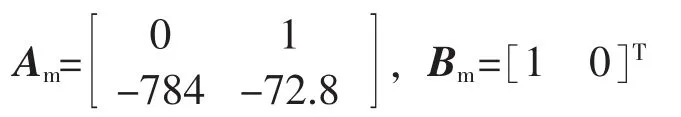
对于给定的Am具有很好的稳定性，便于计算，可以取Km=0。

b.取d0=0.28，则可以得到：

对于任意的给定正实矩阵Q满足李雅普诺夫方程：

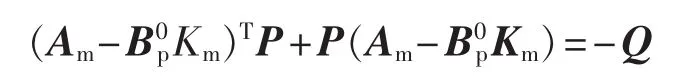
可以解得对称正实矩阵：

c.根据正实引理可以得到：

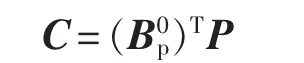
d.由充分条件可以得：

e.为了满足波波夫积分不等式，根据文献[18]选用比例适用律：

其中，L、M、N、O均为非负定对称矩阵。

4 仿真实验

为了验证提出的自适应控制策略在单相并联APF控制中的正确性和有效性，本文设计了在MATLAB环境下的仿真实验，与传统的PI控制策略进行了比较研究。系统参数如下：理想电网电压us幅值为220 V，频率为50 Hz；电网等效阻抗Ls为0.05 mH；滤波电抗器L为5 mH；直流侧电容C为5000 μF；直流侧电容电压参考值Udc为1000 V；直流侧PI控制器参数 kp=10，ki=4；PWM 频率为 10 kHz；单相整流桥负载为10 Ω电阻串联10 mH电感。直流侧电压的稳定采用了PI控制进行实现。

图3为APF未投入时，PCC处的电压波形和负载电流波形。对负载电流进行频谱分析可知其中含有很多谐波，谐波畸变率THD=18.67%，畸变程度很严重。采用本文提出的自适应控制策略和PI方法分别进行补偿，稳态时电网电流波形如图4所示。经过分析和对比可见，2种方法均能对电网谐波进行有效的抑制，但本文提出的控制策略比PI控制策略的谐波补偿效果更好。

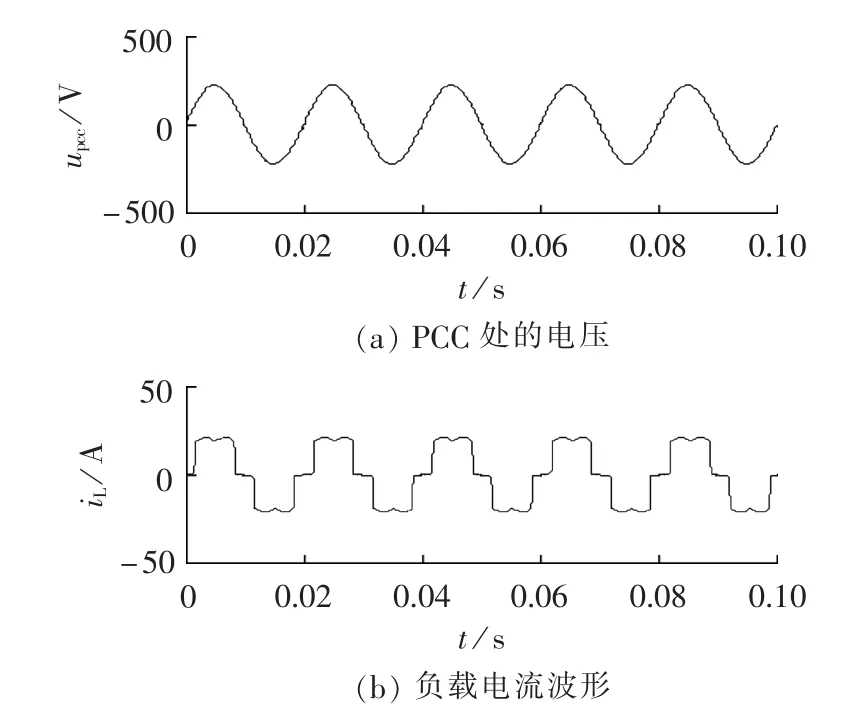
图3 PCC处的电压和负载的电流波形Fig.3 Waveforms of voltage at PCC and load current

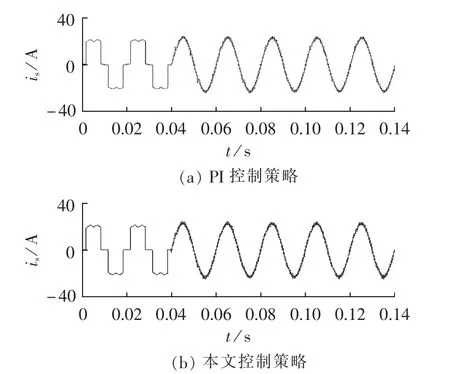
图4 采用PI和本文控制策略补偿后的电网电流Fig.4 Grid currents after compensation with PI control and proposed control strategy

在负载不变的基础上，考虑电网等效阻抗的不确定性对APF补偿效果的影响。假设L的变化范围为2～8 mH。这2种情况下采用PI控制和本文所提控制策略补偿后系统电流波形图如图5、6所示。当L=2 mH时2种算法控制下的THD分别为3.19%和2.37%；当L=8 mH时2种算法控制下的THD分别为5.14%和4.35%。由此可以看出本文所提控制策略对电网等效阻抗的不确定性具有更好的鲁棒性。

图5 当L=2 mH时采用PI和本文控制策略补偿后的电网电流Fig.5 Grid currents after compensation with PI control and proposed control strategy，when L is 2 mH

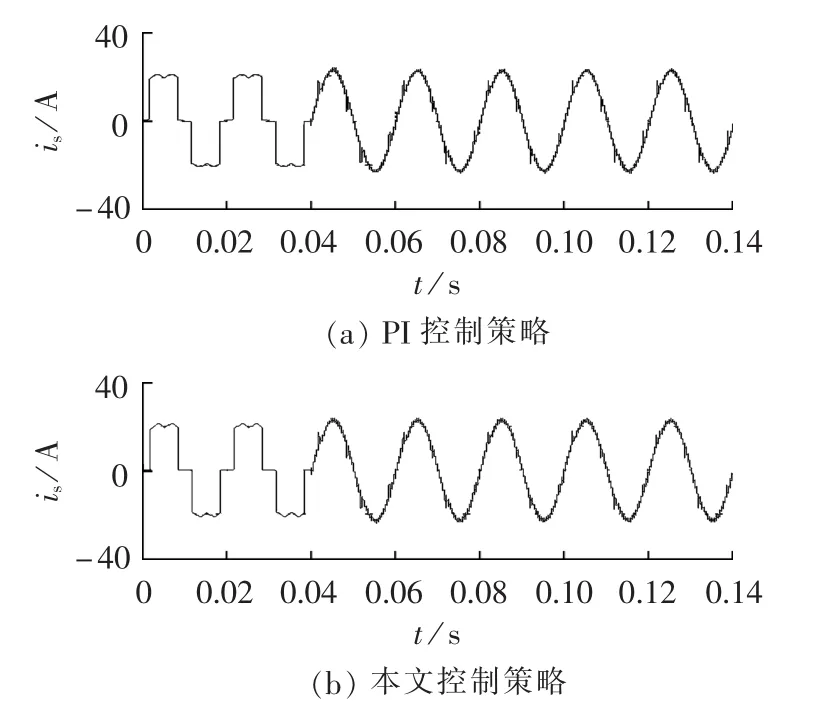
图6 当L=8 mH时采用PI和本文控制策略补偿后的电网电流Fig.6 Grid currents after compensation with PI control and proposed control strategy，when L is 8 mH

5 结论

本文针对单相并联APF进行研究，将基于超稳定理论的模型跟随控制策略应用到单相APF中。先将系统等价于一个反馈系统，包括前向环节和反馈环节，前向环节的传递函数严格正实，而反馈环节满足波波夫积分不等式，由此可以设计出系统的自适应控制律，保证APF的输出电流对负载谐波电流的跟踪。当滤波参数发生变化时，本文提出的控制策略比PI方法具有更好的谐波补偿效果，对参数扰动具有更强的自适应和鲁棒性。