基于疲劳热耗散试验的金属温度场分析方法

陈维维，薛红前，封 硕

（西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072）

0 引言

金属疲劳过程中伴随有很多种形式的能量耗散，热耗散便是其中之一。众所周知，疲劳能量理论研究经历了两个阶段：机械能耗阶段和能量耗散阶段[1]。随着精确的测量方法的不断涌现以及大量先进的非接触式测温仪的应用，疲劳能量理论的研究逐渐摆脱单纯的机械能耗阶段，进入以热耗散为主的能量耗散的研究阶段。目前有大量的经典理论认为疲劳过程的热大部分是由于内摩擦引起的，且塑性变形会引起原子震荡，使得能量大部分转换为热，因此热耗散与塑性变形有关。同时塑性变形又会使材料显微结构发生不可逆的变化，使材料产生疲劳损伤。

Luong[2，3]指出红外热像不仅能够确定损伤的位置和演化过程，而且能够观察损伤和破坏的物理过程，快速确定材料的疲劳强度[4，5]。Boulanger[6]利用红外照相机研究了钢在疲劳过程中的热弹性效应和热耗散。Charles[7]用热像仪监测双边缺口钢试样的表面温度分布，发现疲劳寿命包含三个热耗散阶段，分别对应于不同的损伤状态。这三个阶段（phase I，phase II，phase III）在 Risitano[8]的论文中有详尽论述。童小燕[9]用红外热像仪测量了低周疲劳自然温升分布及变化规律，并再现了温度的涨落。意大利学者G.Meneghetti[10]建立过金属热耗散模型，该模型给出了单位体积材料单个循环的热耗散能。他们的研究结论还不统一，每种理论都在一定范围内有效。完备的疲劳热耗散理论体系和普适预测方法还没有出现。有些情况下的疲劳温度场和热源的变化还不能够准确预测。

鉴于此，本研究试图提出一种快速简便并行之有效、节省时间和试验成本的疲劳热耗散温度场预测方法。以基本热力学理论和G.Meneghetti等人的成果为基础，综合考量了金属材料的微观属性（晶粒度）和宏观热学、力学性能，给出了针对疲劳试验的当量热源模型以及快速预测疲劳热耗散温度场的方法。该方法和模型以试验为基础，但不完全依赖于试验。它可靠地反映出不同晶粒度、不同载荷水平、不同加载周次情况下的温度场分布。

1 试验

1.1 材料成分及基本热学力学性能

所有300M超高强度钢试件的化学成分（质量分数%）：碳 0.38、锰 0.76～0.91、硅 1.51～1.69、硫 0.003、磷0.0075～0.0085、镍1.8～1.91、铬0.85、钒0.07～0.085、铝0.4、铜0.07、余量铁。部分试件采用标准热处理工序：预备热处理925℃正火+680℃～700℃高温回火和最终热处理870℃油淬+300℃回火2次，空冷[11]。其余试件未进行热处理。疲劳试件做成变截面圆柱形，最小处直径为5mm。其余各部尺寸如图1所示。表1给出了300M钢的力学性能。

1.2 ASTM平均晶粒度测量

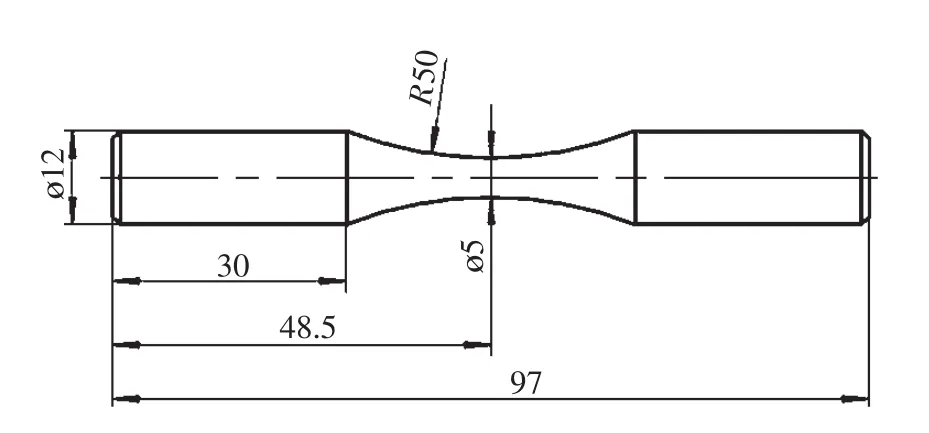
图1 疲劳试样几何尺寸

本研究所采用的晶粒度标准为ASTM（美国材料试验学会）制定的确定金属晶粒度的相关标准（ASTM_E112_2004）。依据ASTM_E112_2004的要求将金属试件表面研磨平整，抛光。使用奥林巴斯金相显微镜GX51（如图2所示），对处理过的试件表面进行观测，并借助金相分析软件UMS300m3对试件进行分析。发现经过热处理的300M钢试件的ASTM平均晶粒度为6.5级，未经热处理的300M钢试件的ASTM平均晶粒度为4.0级。晶粒的大小能够影响金属强度，疲劳寿命等等机械性能，晶粒度越细小，金属强度越大。

表1 300M钢的热学和力学性能

图2 奥林巴斯金相显微镜GX51

1.3 疲劳热耗散试验设备及方法

试验设备实物如图3所示。试验采用INSTRON8801液压伺服疲劳试验机，采用应力控制恒幅加载方式，控制波形为正弦波，加载频率20Hz，应力比R=-1。同时采用Thermal CAM SC3000热红外成像仪测量试样表面温度在疲劳过程中的变化，该热像仪波长8～9μm，具有极高的热灵敏度，测量精度可达到0.003℃。首先选取经过热处理和未经过热处理的各一个试件进行静拉伸试验，得到位移-载荷曲线和热耗散曲线。然后再分别取热处理和未热处理的试件，在不同的应力水平下进行疲劳试验，记录其疲劳过程和热耗散规律。

图3 INSTRON 8801疲劳试验机和Thermal CAM SC3000热成像仪

1.4 试验结果

整理试验数据发现温度和循环周次之间的关系大致如图4所示。可以发现，温度随循环周次的变化大致可分为三个阶段：初始温升阶段，平稳阶段和最后断裂前的急剧上升阶段。

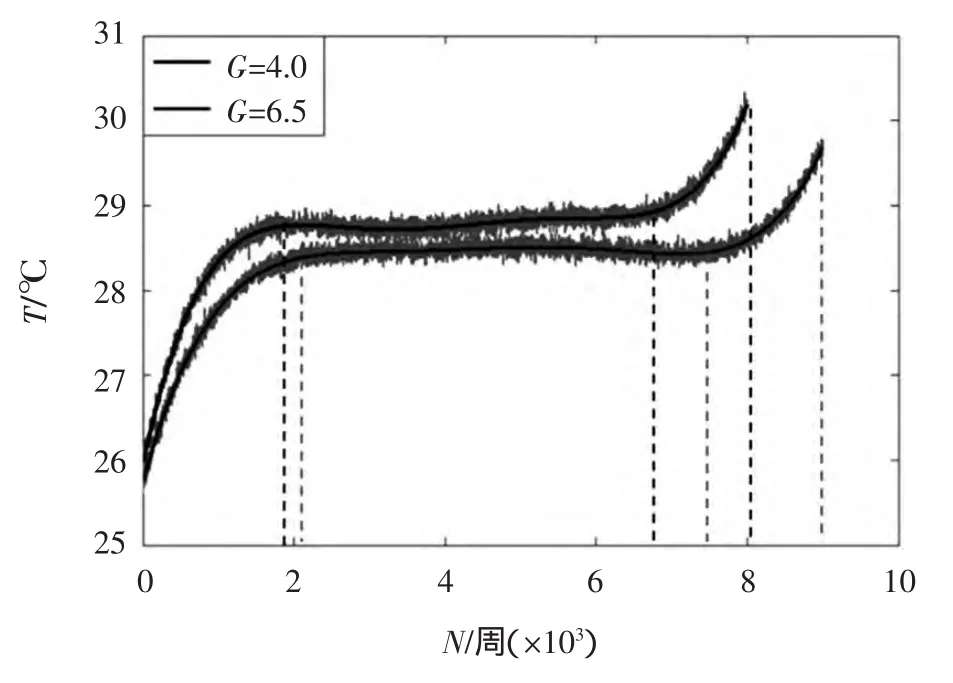
图4 疲劳温度演化图（N表示循环次数，T表示试件表面温度）

初始时由于循环次数较小，温度只有小幅上涨。初始温升表现在材料对位错的突然运动和伴随着表面挤入和挤出的缺陷。在这一阶段，位移幅值越大，初始温升斜率越大。第二阶段，循环应力应变响应变得稳定，因此滞回环能的产生和热耗散达到了一个平衡，平均温度达到一个稳定的状态。值得注意的是，在这一阶段，某些情况下温度有轻微的下降，这是由于宏观裂纹形成，产生新表面使周围环境耗散热[12]。第三阶段温度快速增长直到发生失效。在这一阶段，由于裂尖应力集中导致的大塑性变形，形成宏观裂纹，温度突然增加，也就是说，产生的塑性变形功大部分转变成热。裂尖塑性变形导致试件断裂位置处温度的不均匀[13-15]。这一突然上升的温度可以作为即将断裂的预警。

同时，从图4可以看出，晶粒越粗大，温度上升越快。这是因为晶粒粗大，晶体间的贴合和连接不如经过热处理后的具有高晶粒度的试件，从而造成了更大的摩擦，产生更多的热。

2 建模分析

2.1 疲劳热耗散温度场模型建立

疲劳过程是一个能量耗散过程。而热耗散是整个能量耗散过程中比重很大的部分。材料形变过程中的热耗散是由内摩擦引起的，即晶体（晶粒）一部分相对于另一些部分的晶内剪切移动摩擦而产生热。另外，应变能增加了位错的不稳定性，加剧了位错的运动。运动位错将原子震荡，使能量大部分转换为热。材料中能量的存储机制包括点阵畸变和点阵缺陷，其中点阵缺陷占绝大部分[16]。材料的点阵缺陷主要包括位错、空位、形变晶界等。由于点阵缺陷的形成和分布非常复杂.并且各种缺陷之间还存在复杂的相互作用，因此从微观角度去定量研究材料疲劳过程中的热耗散状态是不现实的。不同的晶粒大小和组织结构会造成在摩擦，剪切移动，撕裂过程中生成热量的不同。对同样几何规格同样材料不同晶粒情况的试件，在同样载荷和频率下生成的热量也不一样。本研究试图提出一种包含金属材料宏观性能指标和微观性能指标，且简便易行，精准可靠的温度场定量预测模型。由此出发，这里将载荷水平σ，疲劳周次N，以及平均晶粒度G作为主要考量指标。

首先将经过热处理和未经过热处理的试件分别进行分析。在确定的晶粒度水平G下，各组试件在疲劳热耗散试验过程中，每个载荷水平下试件有特定的温度变化状况，不同的循环周次也对应了特定的温度场情况。换言之，每个载荷水平下，某个循环周次时，某个特定平均晶粒度的试件有一个特定温度场。因此，本文将载荷水平σ和疲劳周次N作为本模型的自变量（二者皆为S-N曲线的参量，也是描述疲劳的根本指标）。由多元函数逼近[17]方法构造曲面方程：

式中，ΔTG表示温度变化，a0，a1，……，a9为与材料属性有关的待定系数，B为噪声修正项，通常可视为无穷小量并忽略。

本研究中，由于实验数据量较大，故没有采取普通的点数和待定的曲面方程系数一样数量的多元函数插值来求待定系数和绘制曲面，而是利用了数据多的优势，尽可能多得将数据回代入（1）式，构造矛盾方程组，求出各个待定系数的最小二乘解。这样得到的系数兼顾了尽可能多的数据信息，并且全局性更好，“坏点”和局部不良扰动对待定系数的影响也被减小。试验中在每一个应力载荷下（共七个应力水平）的试验数据中随机取出50个点，由于phase I和phase III两个阶段的温度变化趋势复杂，故取点相对较多，而phase II相对平缓，故取较少的点就能反映其趋势。

本研究代入了350个点的数据值之后，得到两组试件温升曲面方程的系数。

G=6.5（经过热处理）的300M钢试件的温升曲面系数：

a0=0，a1=0.5816，a2=0.3826，a3=0，a4=-0.0012，a5=-0.0008，a6=0，a7=0，a8=0，a9=0。

G=4.0（未经过热处理）的300M钢试件的温升曲面系数：

a0=0，a1=0.8948，a2=10.369，a3=0，a4=-0.0041，a5=-0.0219，a6=0，a7=0，a8=0，a9=0。

那么，忽略B之后，（1）式就可写成

该式为G=6.5的温升曲面方程，记为式（2）；

同样，未经热处理的温升方程可以写成

该式为G=4.0的温升曲面方程，记为式（3）。这两个方程所刻画的曲面如图5所示。

虽然在试验时G=6.5的这组试件的加载水平是G=4.0的二倍，但其温升水平基本上在一个水平上（都为5℃左右），两者的温升方程绘出的曲面也能发现这一点，换言之，晶粒度高的试件温升水平相对较低，晶粒度低的试件温度上升比较剧烈。这主要是因为晶粒度较低的试验件晶粒比较粗大，晶体间的贴合和连接不如经过热处理后的具有高晶粒度的试件，从而造成了更大的摩擦和储能。

2.2 当量热源模型

本研究中针对试验中的热耗散现象，提出当量热源的概念。所谓当量热源就是指在应力最集中处的几何中心或者在温度最高区域给出一个一定功率的点热源，该热源能够随时间变化并且具有与疲劳试验过程相同的温升变化。2.1节给出的温升模型也是描述这一点的温升。根据能量平衡方程可知，在只考虑热耗散作用时，对于固体金属，有如下关系：

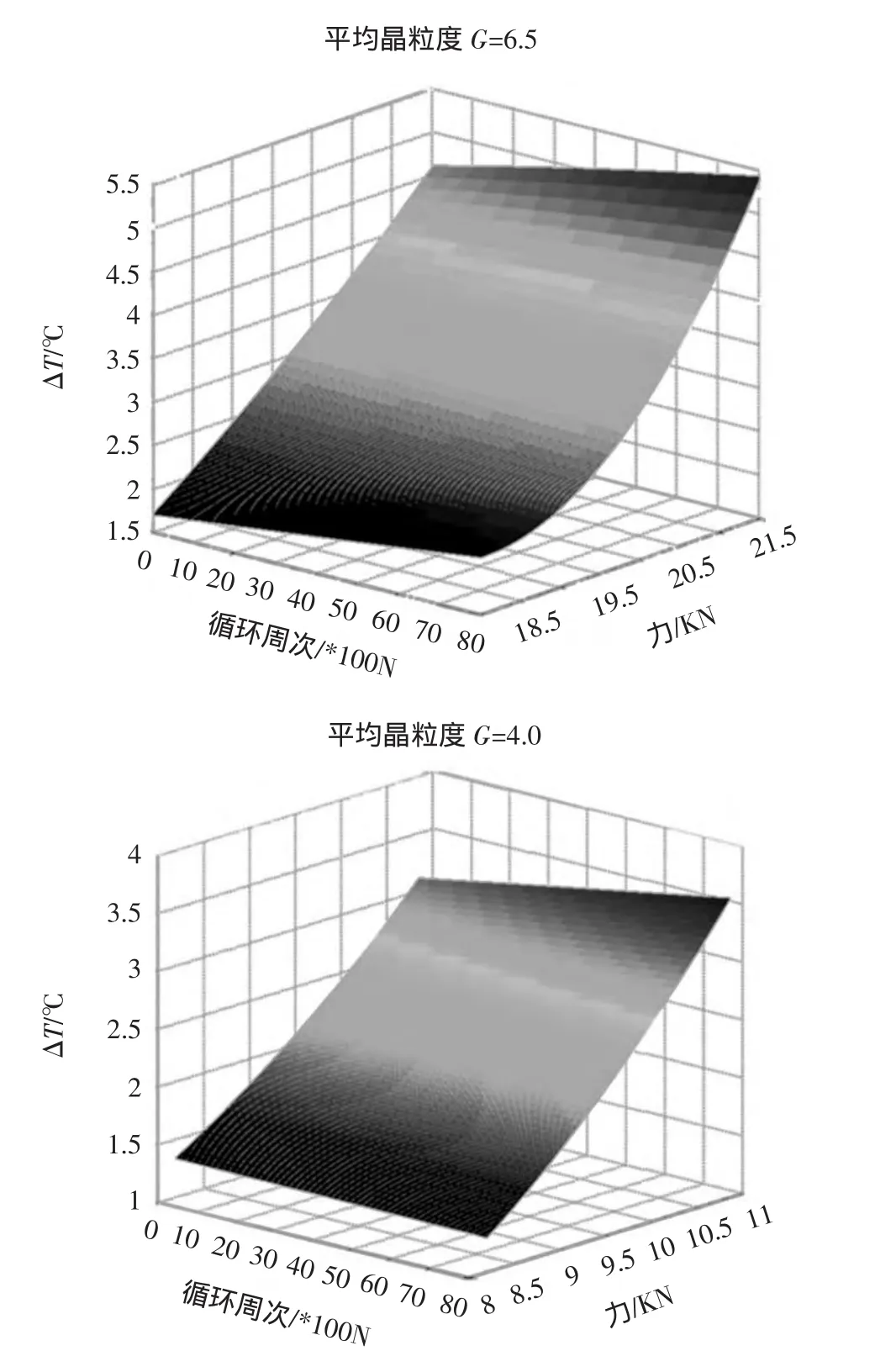
图5 温升方程所表示的温升曲面

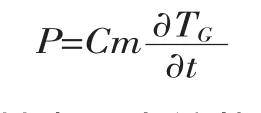
其中P为该热源的瞬时功率，单位W；C为导热介质的比热容，单位J/（kg·K）；m为导热介质的质量，单位 kg。∂TG/∂t为导热介质的温度变化，∂TG/∂t＞0时，过程吸热，反之过程放热。本文中的温升模型已经由实验数据拟合给出，则整个热耗散过程中的功率变化就可求出，则瞬时功率P可以表达为：

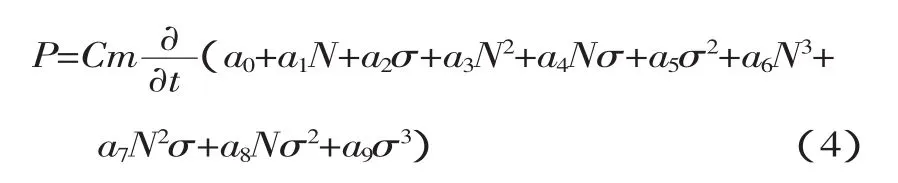
根据能量守恒定律和傅立叶定律可以得出物体内温度场的数学表达，对物体内部的微小单元有：

将P代入上式并消去dxdydz得到：

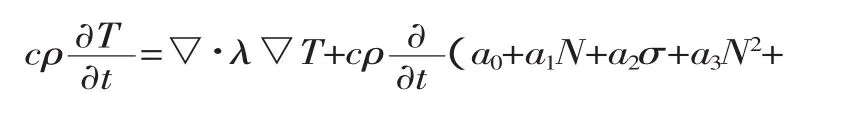
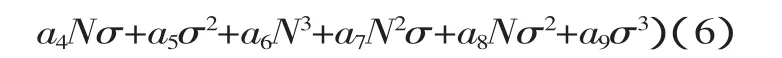
将式（2）、（3）代入式（6）得到晶粒度 G=6.5 和G=4.0时的当量热源方程。

G=6.5时的当量热源方程：

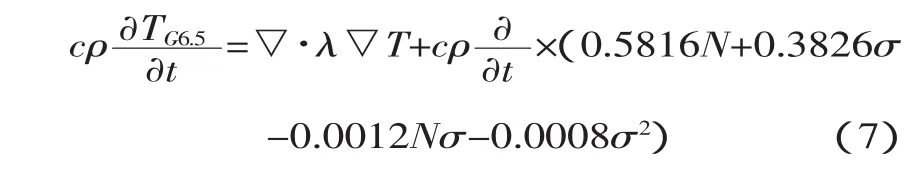
G=4.0时的当量热源方程：

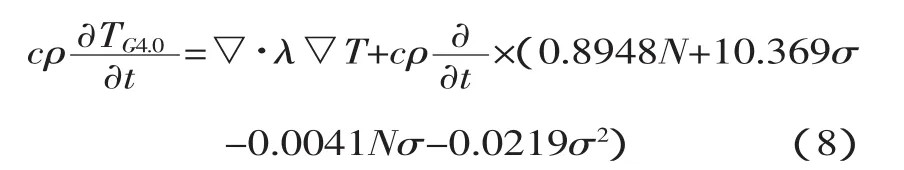
2.3 模型应用分析

经过对比可以发现晶粒度不仅影响热源和表面温度场的大小，而且因为影响材料的疲劳寿命，进而影响温度曲面的范围。模型所构成的曲面的外围边界在S-N平面上的投影恰好是该材料在同样加载状况下的S-N曲线，另外两侧的边界为载荷轴和循环周次轴。晶粒大，则温升曲面向远点靠拢，温度较高；晶粒小则温升曲面朝着S和N都变大的方向扩展，在同样载荷和循环周次下，对同种材料，晶粒细小的温度要低于晶粒粗大的。观察方程的系数可以发现，在晶粒度较低的情况下，周次N和应力σ对温度变化的影响都较大。并且应力还会通过二次项对温升进行影响，而周次对疲劳的影响主要是通过一次项和与应力载荷的交叉项（共同作用）来影响温度升高。

根据不同的晶粒度可以做出不同的温升方程曲面组，当晶粒度值足够丰富时，可在不同的晶粒度的温升曲面之间进行插值计算，求出所需晶粒度的材料在一定的载荷水平和循环周次下的温度升高情况。由于本研究还没找到足够的证据支撑不同的晶粒度带来的温升是线性趋势，故插值不能简单的线性插值。就近似而言，可以在小范围内认为是线性情况。

经过对比发现，两个温升曲面能够反映出晶粒小的材料对外载的抗力较大。要注入更多的机械能才能制造足够的晶界摩擦和位错运动，进而导致较高的温升。故此，从晶粒度的角度来分析疲劳热耗散能够发现，金属材料的晶粒度决定储能与热能的多少。

综上，可利用有限的实验数据，对需要定量确定某一个载荷水平，某个周次时的试件温度场，可以直接对曲面进行插值求解。得到当量热源在某时刻的功率并推演整个温度场情况。该方法简单，可靠。能对疲劳热耗散造成的影响进行预测，对散热结构设计和抗疲劳结构设计有指导意义。

3 数值模拟验证

对经过热处理（晶粒度G=6.5）和未经热处理（晶粒度G=4.0）的试件各取了4组进行新载荷水平试验和数值模拟。这里对新加载水平σ=988MPa的热处理试件的情况进行具体说明。

在整个疲劳试验过程中，将实验值和预测值进行了对比，如图6所示。疲劳的全过程中取了a、b、c、d）4个点。由于phase I阶段的温度变化相对剧烈，所以在这阶段取了3个点。而phase II阶段温度变化平缓，那么取较少点即可说明其变化情况，这里取了一个点，d点。图7各栏为左侧为经过热处理的试件在加载水平σ=988MPa时的试验红外观测照片，各组照片拍摄位置与图6相对应。该试验使用同一台试验设备，除载荷水平不同，其他试验参数与之前试验的参数一致。各栏右侧为ANSYS数值模拟的结果。数值模拟时，依据公式（7）给出不同时刻的当量热源的大小。通过色度表的对比可以发现，二者基本一致，试件上垂直方向各个点的温度也非常吻合。除色度对比之外，还进行了数值对比（图7），图中左为试验对比色度条，右为ANSYS模拟色度条。在热耗散试验过程中取适当的点和模拟的结果进行对比，发现对应点的温升曲线在数据上差别不大，最大误差为8.7%。证明本模型可靠。

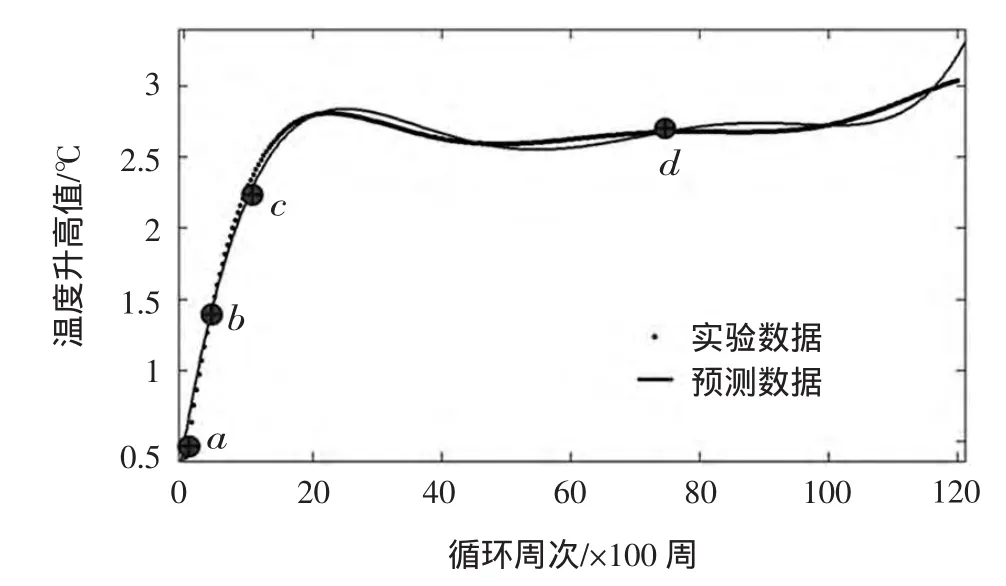
图6 实验值与模型预测结果对比

对比其他的7组验证试验结果发现，最大的验证结果和试验结果相差为13.6%。模型给出的温度预测结果总体相对保守。

图7 试验结果与模拟结果对比图

4 总结

本文论述了一种比较简单可靠的疲劳热耗散温度场定量预测方法。综合考量了微观和宏观两个方面的指标。在实际应用时可根据需求确定需要的试件数量和试验载荷水平的密度进行试验。该方法在一定的范围内能高效地预测疲劳热耗散带来的温度场变化。根据不同的晶粒度可以做出不同的温升方程曲面组，当晶粒度值足够丰富时，可在不同的晶粒度的温升曲面之间进行插值计算，求出所需晶粒度的材料在一定的载荷水平和循环周次下的温度升高情况。

[1]童小燕，姚磊江，吕胜利.疲劳能量方法研究回顾[J].机械强度，2004，26（1）：216-221.

[2]LUONG M.Infrared thermographic scanning of fatigue in metals[J].Nuclear Engineering and Design，1995，158（2）：363-376.

[3]LUONG M P.Fatigue limit evaluation of metals using an infrared thermographic technique[J].Mechanics of materials，1998，28（1）：155-163.

[4]封 硕，薛红前，闫 雪.300M钢疲劳热耗散的试验研究[J].锻压装备与制造技术，2012，47（2）.

[5]陈永兴.基于Fatigue Advisor的冲压模具零件疲劳分析的研究[J].锻压装备与制造技术，2012，47（1）.

[6]BOULANGER T，CHRYSOCHOOS A，MABRU C，et al.Calorimetric analysis of dissipative and thermoelastic effects associated with the fatigue behavior of steels[J].International Journal of Fatigue，2004，26（3）:221-229.

[7]CHARLES J，APPL F，FRANCIS J.Thermographic determination of fatigue damage[J].Journal of Engineering Materials and Technology，1978，100：200.

[8]LA ROSA G，RISITANO A.Thermographic methodology for rapid determination of the fatigue limit of materials and mechanical components[J].International Journal of Fatigue，2000，22（1）：65-73.

[9]童小燕，王德俊，徐 灏.低周疲劳损伤过程的自热温升变化特征[J].金属学报，1991，27（2）：149-152.

[10]MENEGHETTI G.Analysis of the fatigue strength of a stainless steel based on the energy dissipation[J].International Journal of Fatigue，2007，29（1）：81-94.

[11]300M钢性能数据手册.航空航天第六二一研究所.1991.

[12]RICE J，DRUCKER D C.Energy changes in stressed bodies due to void and crack growth[J].International Journal of Fracture Mechanics，1967，3（1）：19-27.

[13]JIANG L，WANG H，LIAW P K，et al.Characterization of the Temperature Evolution during High-Cycle Fatigue of the ULTIMET Superalloy:Experiment and Theoretical Modeling[J].Metallurgical and Materials Transactions A，2001，32：2279-2296.

[14]YANG B，LIAW P，WANG H，et al.Thermographic investigation of the fatigue behavior of reactor pressure vessel steels[J].Materials Science and Engineering:A，2001，314（1）：131-139.

[15]YANG B.Thermographic detection of fatigue damage of reactor pressure vessel（RPV）steels[J].Journal of Materials Engineering and Performance，2003，12（3）：345-353.

[16]MARTIN J，RD D.金属系中显微结构的稳定性[M].李新立.北京:科学出版社，1984.

[17]王仁宏.多元函数逼近[M].北京：科学出版社，1988.