二自由度九杆传动机构参数对曲柄扭矩的影响
2014-09-25莫健华王宗强
闫 辉,莫健华,张 晨,王宗强
(华中科技大学 材料成形与模具技术国家重点实验室,湖北 武汉 430074)
1 引言
机械式精冲压力机的传动系统是一种二自由度九杆机构,一般采用单台普通电机通过变速箱、带传动、蜗杆蜗轮和一对双边斜齿轮减速后驱动二自由度九杆机构。变速箱为无级变速,压力机可在一定范围内获得不同的冲裁速度和相应的行程次数。但这样的精压机一旦结构尺寸和参数确定,滑块的行程曲线就不能按照工艺要求任意改变[1]。
近年来,随着伺服电机和伺服控制技术的发展,在传统压力机基础上开发新型伺服压力机已渐成趋势[2][3]。Yan Hongsen等[4]在Watt压力机基础上利用伺服电机代替普通电机驱动传动机构,开发出了新型伺服压力机。Yossifon S和Shivpuri R[5]等开发出了以伺服电机驱动双曲柄的双肘杆伺服压力机。黄海波提出了在传统精压机传动机构的基础上,用两台伺服电机代替一台普通电机,驱动二自由度九杆机构的方案。在两台电机同步控制时,通过改变两台电机的起始相位差,以获得多种形式的滑块运动曲线,实现用户在现场可任意改变滑块运动规律的驱动柔性化[6]。
直接用伺服电机驱动传动机构,因去掉了飞轮会导致功率增大问题。本文通过优选上述传动机构中三角板的尺寸,以优化两台电机的扭矩分配,使两台电机的功率分配趋于均衡,解决单台电机功率过大的问题。
2 虚拟样机模型
根据瑞士GKP系列传统精压机九杆传动机构[7]及黄海波的模型[6],建立如图1所示传动机构倒置的虚拟样机模型。由于去掉了飞轮等辅助传动机构,传动部分整体重心得以降低,所以本文采用上传动方式,即滑块冲压方向为从上到下,这样布置还有利于简化模具及送料装置设计。图1中各杆件尺寸如表1所示。
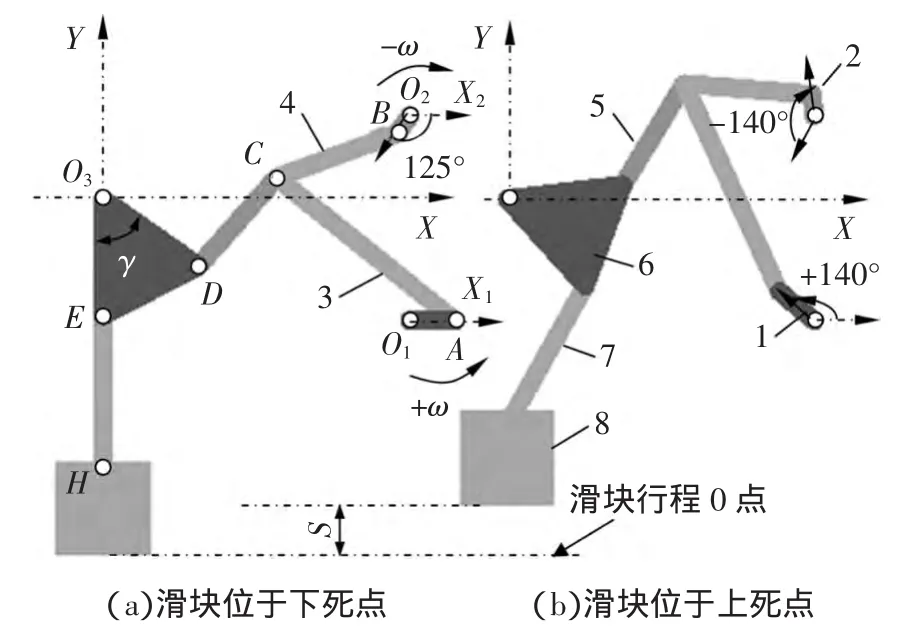
图1 九杆机构虚拟样机模型
2.1 样机模型初始化定义
(1)如图1a所示,将滑块在下死点的位置设为样机初始位置。曲柄1的初始位置设在X1上,曲柄1以180d/s的速度逆时针转动;曲柄2的初始位置设在与水平轴 X2呈-125°夹角的轴上,曲柄2以180d/s的速度顺时针转动。
(2)曲柄转角的起始位置设为X1轴正方向,为便于作图分析,曲柄1与曲柄2的转角均规定为正角,如曲柄1初始转角为0°,曲柄2初始转角为125°。从下死点开始,两曲柄各转动140°后到达上死点。
2.2 工艺参数设定
参照同等规格的瑞士GKP系列精冲压力机技术参数[7],设定九杆机构样机模型的工艺参数如表2所示。

表2 九杆机构样机模型工艺参数
2.3 传动机构的压力放大曲线及扭矩曲线
完成上述九杆模型的建模及初始化工艺参数设定后,运用ADAMS软件进行仿真计算。仿真时两曲柄同步转动,且无起始相位差。考虑到要测量滑块回程时电机的扭矩曲线,给滑块设定2t的重量。
由图1可知,曲柄1、2和连杆1、2组成五杆机构将两台电机的运动和扭矩混合后经浮动杆CD传递给由三角板6和连杆3组成的肘杆机构,最后传递给滑块,从而输出所需运动和压力。为研究九杆机构放大特性,假设在滑块由上死点到下死点全行程范围内加载1000kN公称压力,获得滑块在整个行程中曲柄1、2扭矩曲线及载荷放大比曲线,如图2所示。这里将载荷放大比定义为公称压力与浮动杆上所受载荷的比值,即载荷放大比=1000kN/FC,FC为浮动杆CD输入端C点处受到的力。
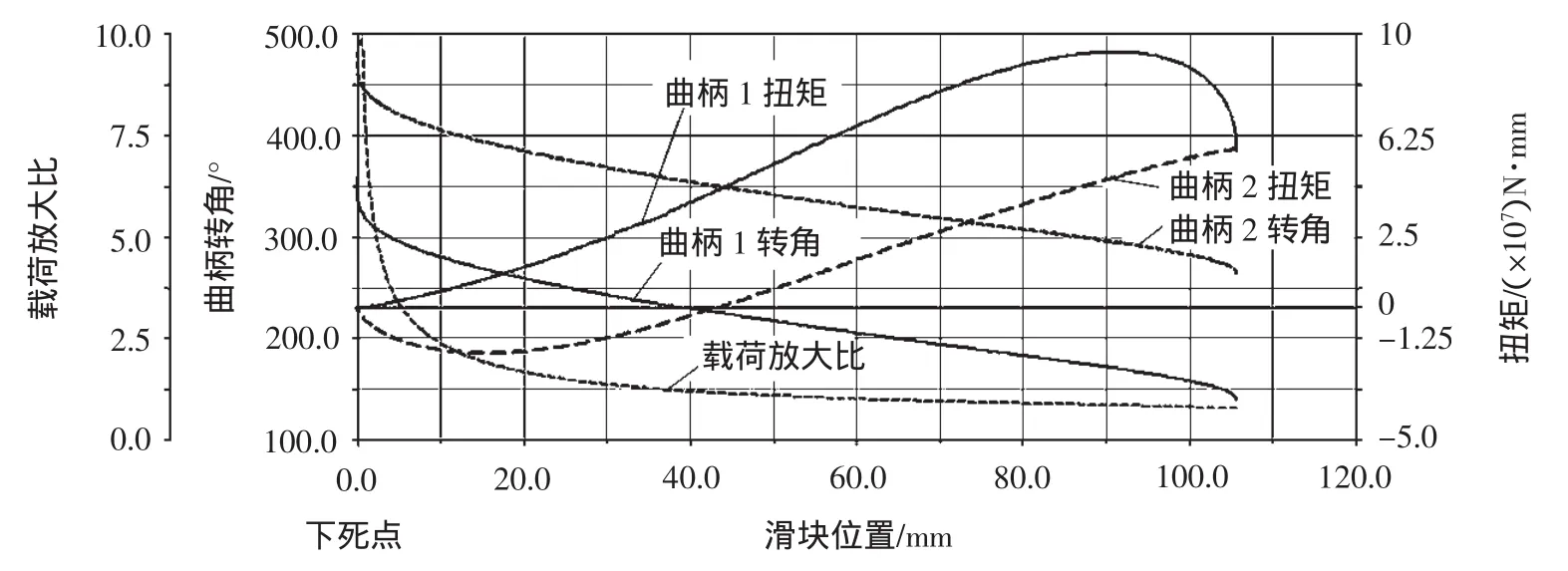
图2 恒定负载状况下的扭矩曲线及载荷放大比
图2 中横坐标为滑块的位置,左边纵轴依次为载荷放大比、曲柄转角,两曲柄同步转动,转角均为正,转角始终相差125°。右边纵轴为曲柄扭矩。
由图2可知,该九杆机构的载荷放大比曲线实际上与滑块压力输出曲线形状是一致的,均为典型的肘杆机构压力输出曲线,即在远离下死点时输出压力很小,压力随着滑块逐渐接近下死点而增加,理论上在下死点时输出压力是无穷大。
分析曲柄1的扭矩曲线可以看出,在滑块向下行程中曲柄1上的扭矩先增大再逐渐减小,下死点时减到最小,整个过程扭矩方向保持不变,其中峰值扭矩出现在曲柄1与连杆1相互垂直的位置,此时曲柄转角为170°;分析曲柄2的扭矩曲线可知,在下行过程中曲柄2上的扭矩不断减小,一直减到0,然后开始反向增加,在接近下死点时又逐渐减小,峰值扭矩出现在曲柄2与连杆2相互垂直的位置,此时曲柄转角为265°。
苏穆武用嘴努努苏越,苏越捅捅徐芬,徐芬急了:爸不是让你说吗?你捅我干啥?苏越无奈,咳嗽了一声,说:婷婷,不是哥干涉你,这找个洋人嘛,确实不合适,比如说这双方的生活习惯——苏婷婷说:我们已经习惯了。苏越不说话了,再次捅捅徐芬,徐芬只好接着道:其实爸妈让我们劝你,你应该理解。爸妈都这么大岁数了,怕你嫁给洋人,以后出了国看不见闺女。苏婷婷说:杰克已经答应了,婚后定居中国。
图2中的曲线是在假设滑块在全行程均受到一恒定载荷时得到的曲线,实际冲压过程中,并不会出现上述分析中的峰值扭矩,滑块只在公称压力行程内输出所需的压力。只要保证在公称压力行程内,电机可提供曲柄所需的最大扭矩,即可保证滑块在公称压力行程内输出公称压力。本文研究内容即降低公称压力行程内两曲柄上的最大扭矩,并尽可能使其分配均衡,从而降低单台电机所需最大功率。
3 传动机构力的放大原理
如图3所示,DO3E为图1中传动机构的三角板三个受力点的连线,F1为浮动杆CD作用到三角板上的力,F2为连杆3对三角板的反作用力。假设某一瞬间传动系统处于动态平衡状态,以三角板为分析对象,由力矩平衡得 F1×l1=F2×l2,变形得:

式中,l1为 F1对 O3的力臂,l2为 F2对 O3的力臂,在冲压过程中连杆3将F2直接传递到滑块上。由式(1)知,在输入端驱动不变的条件下,通过改变DO3E的结构增加l2或者减小l1可以增加F1。由图可知,增加O3D的长度可以增加l1,减小O3E的长度可以增加l2,所以通过改变DO3E的尺寸可提高机构的放大特性。

图3 传动机构力的放大原理
4 传动机构的仿真
为验证上述图3中通过改变DO3E尺寸可提高机构放大特性的设想,建模时将三角板参数化,并设O3D为L1,O3E为L2。仿真时双曲柄同步转动的条件不变,且转速为180d/s,这样滑块的行程次数保持30min-1不变。
4.1 增加L1长度对行程和扭矩的影响
L1原长为245mm,通过增加L1得到一组不同的仿真结果,仿真中用到的L1的值如表3所示。

表3 公称压力行程内最大扭矩
4.1.1 滑块行程及速度曲线
由图4可知,在下行行程内,开始时滑块以较大的速度快速合模,在接近下死点的冲裁阶段滑块速度逐渐减小,完成冲裁后滑块快速回程,滑块的这种运动特性符合精冲工艺对滑块速度特性的要求。进一步研究可知,随着L1增加,滑块的行程降低,当L1增加到334mm时,滑块行程减小到70mm。同时,随着L1增加,回程阶段的最大回程速度也在降低,但由于滑块的行程次数不变,所以并不会影响到压力机的工作效率。
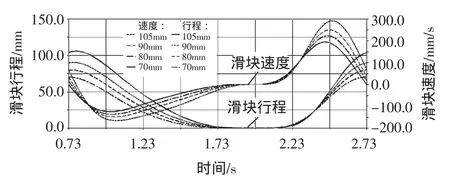
图4 滑块行程及速度曲线
4.1.2 全行程负载下曲柄1、2的扭矩曲线
图5为增加L1后得到的一组仿真结果,L1长度与滑块行程的对照见表3。在全行程负载下,随着L1增加,两曲柄上的峰值扭矩都减小,扭矩整体表现出减小的趋势。在公称压力行程内,曲柄1的扭矩随着L1增加逐渐增大,且对于某一确定的L1值,扭矩是单调减小的;曲柄2的扭矩随着L1增加逐渐减小,对于某一确定的L1值,扭矩不是单调变化的,反向的最大扭矩可能落在公称压力行程内,也可能在公称压力行程外,即反向最大扭矩的位置可能在10mm的左侧,也可能在10mm的右侧。

图5 恒定负载状况下的扭矩曲线
取曲柄1、2在公称压力行程内各自的最大扭矩。对于曲柄1即取10mm处的扭矩值;对于曲柄2取10mm处扭矩值与反向最大扭矩值两者中较大的一个,具体见表3。表中扭矩的正负只反映方向,扭矩和为扭矩1和扭矩2绝对值之和。
由表1知,随着L1的增加,行程减小,扭矩和逐渐减小,这表明增加L1,可以提高机构的放大性能。单独分析两曲柄上的扭矩变化,可知随着L1增加,扭矩1呈增大趋势,而扭矩2逐渐减小,所以从电机选择的角度考虑,并不是扭矩和越小越好,需要兼顾两曲柄上的扭矩,使其尽可能均衡,不至出现其中一个电机扭矩很小,另一个电机扭矩却很大的情况。通过计算将曲柄端扭矩换算为电机功率对比更为明显。计算公式如下:

式(2)为电机功率与输出扭矩之间的关系,其中P 单位 kW,T 单位 N·m,n单位 min-1;式(3)为在不考虑能量损失的前提下减速器输入扭矩与输出扭矩间的关系,其中T1为输入端扭矩,与电机输出扭矩相等;T2为输出端扭矩,与曲柄承受的扭矩相等。曲柄转速为30r/min,计算得到不同行程下所需电机功率,如表4所示。
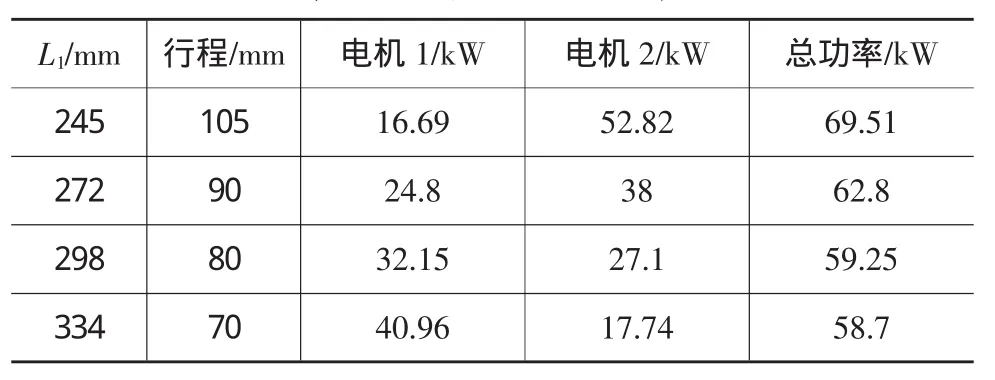
表4 所需电机功率
当行程为105mm时,单台电机最大功率为52.82kW,当增加L1使行程为80mm时,单台电机最大功率可降为32.15kW。如果行程继续减小到70mm,则单台电机功率最大变为40.96kW。所以选择合适的L1长度可降低单台电机的最大功率,使电机功率分配均衡。
4.1.3 回程扭矩分布
图6为滑块空载状况下的回程扭矩曲线。随着L1的增加,曲柄1、2的扭矩总体呈减小趋势,各自的峰值扭矩都减小。取各自的峰值扭矩,如表5所示。

图6 回程扭矩曲线

表5 回程曲柄峰值扭矩
由表5可知,曲柄2峰值扭矩比曲柄1峰值降低趋势明显。与表3中数据比较,可知两曲柄回程峰值扭矩明显小于公称压力行程内的最大扭矩值,因此根据公称压力行程内曲柄最大扭矩计算出的电机功率完全可以满足滑块回程时对电机功率的需求。
4.2 增加L2长度对行程和扭矩的影响
L2原长为245mm,通过减小L2可得到一组不同的仿真结果,仿真中用到L2的值如表6所示。
4.2.1 滑块行程及速度曲线
图7为减小L2得到的一组滑块行程和速度曲线,与图4中增加L1对滑块的行程和速度的影响类似,随着L2减小,滑块行程减小,最大回程速度减小。

表6 公称压力行程内最大扭矩
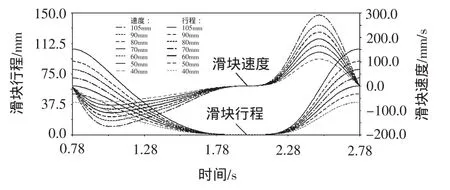
图7 滑块行程及速度曲线
4.2.2 全行程负载下曲柄1、2的扭矩
图8为减小L2得到的一组仿真结果,随着L2减小,曲柄1、2扭矩总体在减小。在公称压力行程内变化规律也与图5中相似,不同的是扭矩1、2的变化幅度没有图5中大,取公称压力行程内扭矩 1、2的最大值,见表6。

图8 恒定负载状况下的扭矩曲线
由表6知,随着L2减小,滑块行程减小,扭矩1增加,扭矩2减小,总的扭矩和减小,这表明,减小L2可以增加机构的放大性。为更直观地分析这种变化,按照公式(2)和(3)将扭矩换算为电机功率作进一步比较,见表7。
分析表7中电机1、2的功率变化,可知其变化趋势明显小于表4中电机功率的变化趋势。以同为80mm行程时为例,表4中电机1、2功率分别为32.15kW、27.1kW,而表7中分别为19.04kW,42.59kW,表4中电机功率的增幅和降幅明显大于表7中。所以通过减小L1增加机构放大性,在滑块行程比较小的时候效果明显,如行程为40mm时,总功率与原行程为105mm相比降低很多,同时单台电机功率也不是很大且分配比较均衡。查阅国内外精冲压力机的技术标准[7],可知这种小行程的传动设计方案是可以接受的。

表7 所需电机功率分配
4.2.3 回程扭矩曲线
图9为不同L2下滑块空载时回程扭矩曲线,随着L2减小,曲柄1、2的回程扭矩都减小,这与4.1.3中增加L1对回程扭矩的影响是一致的。从图中还可以看出曲柄1的峰值扭矩没有超过1.5E6N·mm,曲柄2的峰值未超过-1.0E6N·mm,即曲柄1、2的回程峰值扭矩小于表6中任一扭矩值,所以表7中给出的电机功率一定可以满足滑块快速回程时对电机功率的需求。
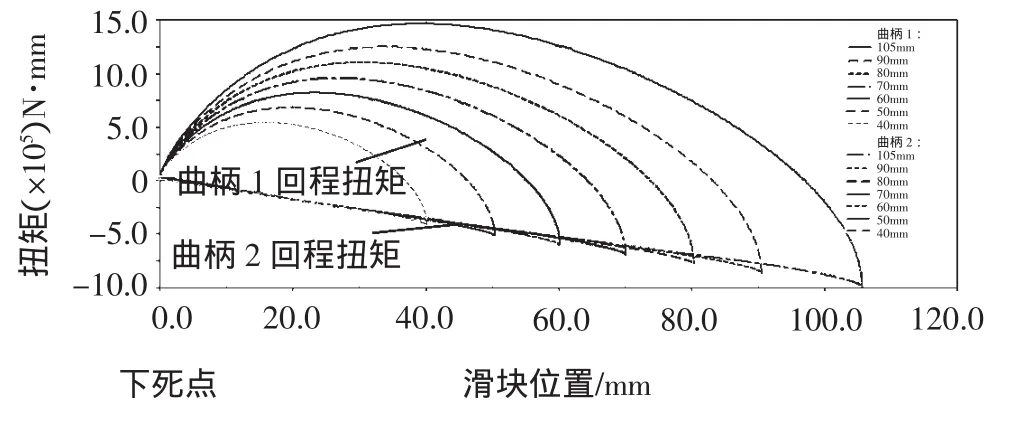
图9 回程扭矩曲线
4.3 同时改变L1和L2对扭矩的影响
综合考虑L1和L2对曲柄扭矩分布的影响。仔细分析表7中电机功率的变化情况,可知当L2减小,使滑块行程每下降10mm,电机1的功率约增加1kW,电机2的功率约减小5kW;再看表4中数据,当L1增加,使滑块行程每下降10mm,电机1功率约增加8kW,电机2功率约减小10kW。根据此规律可以对表4和表7中选定的功率分配比较均衡的方案,通过改变三角板的另一条边长来使功率分配更为均衡。

图10 恒定负载状况下的扭矩曲线
以表4中行程为80mm的方案为例,电机1功率略大于电机2功率,根据以上分析,可以通过减小L2来使功率分布更为均衡。仿真结果表明,当L2=260mm时,滑块行程为90mm,此时得到的电机1功率为31.58kW,电机2为30.4kW,扭矩曲线见图10。由表可见,同时改变L1和L2比表4和表7中行程同为90mm的两种方案中单台电机功率更小。
5 结论
(1)仿真结果表明增加L1或减小L2都可使在公称压力行程内曲柄1上扭矩增加,曲柄2上扭矩减小。通过单独改变L1或L2可使双曲柄上扭矩趋于均衡,从而避免驱动双曲柄的单台伺服电机功率过大。改变L1和L2其效果差别在于,在得到理想的扭矩分配时,得到的滑块行程不同;同时改变L1和L2也可使双曲柄扭矩分配趋于均衡。
(2)在虚拟样机模型中给滑块施加全行程的公称压力,然后分析公称压力行程内曲柄扭矩的变化,这为进一步选取合适功率的伺服电机提供了一种分析方法。
[1]王 平,叶晓苇.冲压加工设备及自动化[M].武汉:华中科技大学出版社,2006.
[2]吕 言,周建国,阮 澍.最新伺服压力机的开发以及今后的动向[J].锻压装备与制造技术,2006,41(1):11-14.
[3]莫健华,郑加坤,古嗣伸裕,等.伺服压力机的发展现状及其应用[J].锻压装备与制造技术,2007,42(5):19-22.
[4]Yan Hongsen,Chen Weiren.A variable input speed approach improving the output motion characteristics of Watt-type press[J].International Journal of Machine Tools&Manufacture,2000,40(5):675-690.
[5]Yossifon S,shivpuri R.Analysis and comparison of selected rotary linkage drive for mechanical presss.[J].International Journal of Machinery Tools Manufacture,1993,(2):175-189.
[6]黄海波,莫健华,吕 言,等.全伺服驱动二自由度九杆机构的同步控制研究[J].锻压装备与制造技术,2012,47(3):30-34.
[7]何德誉.专用压力机[M].北京:机械工业出版社,1989:350-360.
[8]中国机械工程学会塑性工程学会.锻压手册锻压车间设备分册(第三版)[M].北京:机械工业出版社,2008.
