基于Android平台下电机振动信号检测系统的设计
2014-09-25陈江波黄建忠
陈江波,黄建忠
(上海海事大学 物流工程学院,上海201306)
0 引 言
近年来,智能手机已经成为人们必不可少的一种手持设备。随着科技的进步,智能手机通过在手机中嵌入各种传感器,如摄像头、加速度传感器、方向传感器、磁力计、三轴陀螺仪、距离传感器等,开始具备越来越多、越来越强大的功能。开发、利用手机中的这些传感器已经逐步形成了一种趋势。
本文介绍了一种基于智能手机传感器在工业领域中的应用开发案例,在Android平台下开发了基于加速度传感器的应用,即将手机做成测振仪。通过对检测到的电机振动信号的分析,可初步判断电机的运行状况。另外,利用快速傅里叶变换(FFT)对振动信号进行处理,可为进一步更加可靠的判断电机的运行状况提供数据。
1 电机的振动检测
振动是设备运行过程中的普遍现象,特别是旋转设备,无论是正常状态还是故障状态,其运行过程中均会产生振动。例如,旋转电机在运转时由于机械摩擦、转子不平衡、电磁力等原因会使定转子产生振动。显然,振动是许多设备运行时所固有的,其中包含设备运行状态的丰富信息。采集分析这些振动信号,提取有关信息,能够有效地检测电机的运行状态[1]。
传统的振动检测方式,一般是在电机的检测位置安装传感器,将采集到的数据实时传送到上位机,对数据进行实时分析、处理,判断电机运行是否正常。随着科技的进步,各大公司相继开发出了便携式的、用于检测振动参量的测振仪。测振仪可以将检测到的加速度、速度、位移显示出来,通过将测振仪与外接滤波器相连,可对振动信号进行频谱分析。
本案例中选择以速度作为特征量,利用手机加速度传感器,将采集到的加速度信号转换为速度信号,将速度信号数据存储起来,通过调用绘图函数,绘制速度的实时时域波形图,再通过FFT对速度信号进行快速傅里叶变换,绘制速度信号的实时频谱图。分析电机的振动速度时域波形和频谱图,从而判断电机的运行状态。
2 案例的实现
本案例在Eclipse软件下,运用Java语言进行开发,最终的测振仪应用程序界面如图1所示。当点击“Start”按钮时,应用程序开始采集、处理数据以绘制速度的实时时域波形及频谱图,同时,“Start”按钮变为Stop状态,再点击按钮会恢复原来状态,应用程序停止绘图。点击“Clear”按钮会实现清屏,点击“Exit”按钮会进入“是否选择退出”应用程序界面,进而可退出应用程序。现简要介绍一下分步开发的过程。
2.1 数据的采集

图1 测振仪应用程序界面
开发过程中首先要进行数据的采集,Android智能手机中的加速度传感器类型为Sensor.TYPE_ACC ELEROMETER,可通过andr oid.har d ware.Sensor-Event返回加速度传感器的值,其返回值为浮点类型,单位为 m/s2,有三个方向的值,分别是:val ues[0]:x轴方向加速度;values[1]:y轴方向加速度;values[2]:z轴方向加速度。加速度传感器感应加速度的方向大致如图2所示,其中:x方向为手机的水平方向,右为正;y方向为手机的水平垂直方向,前为正;z方向为手机的空间垂直方向,天空的方向为正,地球的方向为负。
另外,需要注意的是,由于地球的重力加速度g(值为9.8 m/s2)的影响,当手机水平朝上放置时,z轴的返回值应为9.8 m/s2,x轴和y轴没有此限制。

图2 PID控制器模型图
要与传感器进行交互,应用程序必须注册以侦听该传感器相关的活动。相关代码如下:
//注册加速度传感器
protected void on Resu me(){
super.on Resu me();
sensor Mg.register Listener(mView,gravity Sensor,Sensor Manager.SENSOR_DELAY_UI);
}
//注销加速度传感器
protected void on Pause(){
super.on Pause();
sensor Mg.unregister Listener(mView);}
上述代码中,在on Resu me()方法中使用对Sensor Manager类的引用通过register Listener方法注册传感器更新。当应用程序暂停时,在on Pause()方法中使用对Sensor Manager类的引用通过unregister L-istener方法注销侦听器,这样以后就不会再收到传感器的更新。
2.2 数据的处理
加速度传感器传回三个方向上的值,本案例中,只使用y轴的返回值做电机振动的检测。
国家标准和国际标准规定以振动速度作为电机振动等级和规定振动限值。因此,需要将采集到的加速度信号转化为速度信号,本案例中采用梯形法进行加速度信号的转换。
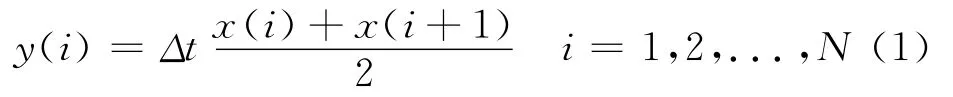
式中,Δt表采样周期;x(i)表示i时刻采样的加速度值;y(i)表示经过梯形变换后得到的i时刻的振动速度。
代码的实现如下:
Long cur Ti me=System.current Ti me Millis();if(cur Ti me-last Update>1){
c1=gravity[1];
c=1*(c1+c2)/2;
c2=c1;
last Update=cur Ti me;
}
上述代码中,先利用System.current Ti me Millis()取得当前系统的时间cur Ti me,当时间间隔为1 ms时(本案例选取采样时间为1 ms),保留原来的数据,同时接收新的数据,按照公式(1)得到的振动速度为c=1×(c1+c2)/2,如此循环下去。
2.3 时域波形图的绘制
将数据处理后以波形图显示,方能更好地观测电机内部的运行状况。本案例中选取采样频率为Fs=1 000 Hz,使用Android开发绘制中的View类进行绘图,将处理后的数据存储在一个数组中,通过调用on-Draw()方法进行实时绘图。具体的实现代码为:
if(mList.size()>=2){
f or(int i=0;i< mList.size()-1;i++){
canvas.drawLine(mList.get(i).x,OFFSET_TOP+CHAR/2-mList.get(i).y*CHARTH/10000,mList.get(i+1).x,OFFSET_TOP+CHARTH/2-mList.get(i+1).y*CHARTH/10000,paint);
}
}
上述代码中,将处理好的数据存入对象mList中,当mList中的数据大于等于2时,使用on Draw()方法中的canvas.drawLine进行绘图。
另外,在主线程之外,又创建了一个线程,在其中通过调用Invalidate()方法,每隔0.01 ms重新刷新一下屏幕。其实现的代码如下:
public void r un(){
mView.invalidate();
m Handler.post Delayed(t his,(l ong)0.01);
}
2.4 频谱分析
时域波形实际上综合反映了振动信号的振幅、频率和相位。用时域波形来表示振动情况最为简单、直观,并且通过对时域波形的观察,也可以判断出一些常见的故障。但是时域波形图也有其不足之处,即不太容易看出所包含信息与故障的联系。这时需要将时域信号利用傅里叶变换变为频域信号,以频率为变量,对信号进行频谱分析。
在实际采样中所采集的信号是离散的并且是有限的,对数字振动信号进行傅里叶变换时需要采用离散傅里叶变换(DFT)[2]。
N点序列x(n)的N点离散傅里叶变换可表示为
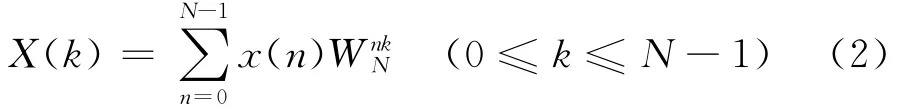
式中,WN=e-j2π/N;x(n)和X(k)可以是实数或复数。
快速傅里叶变换(FFT)是计算离散傅里叶变换的一种快速算法。本案例中采用按时间抽取的FFT算法。令信号序列的长度为N=2 M,其中M是正整数,可以将时域信号序列x(n)分解成两部分,一是偶数部分x(2n),另一是奇数部分x(2n+1),其中n=0,1,2,...,-1。于是信号序列x(n)的离散傅里叶变换可以用两个N/2抽样点的离散傅里叶变换来表示和计算。考虑到W2N=WN/2以及离散傅里叶变换的周期性,式(2)可写成

其中
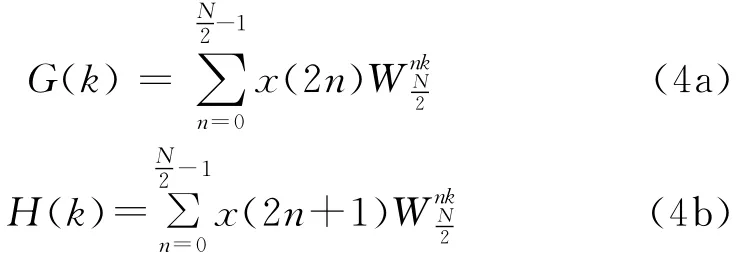
由此可见,式(4)是两个只含有N/2个点的离散傅里叶变换,G(k)仅包括原信号序列中的偶数点序列,H(k)则仅包括它的奇数点序列。虽然k=0,1,2,…,N-1,但是G(k)和 H(k)的周期都是 N/2,它们的数值以N/2周期重复。
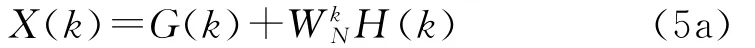
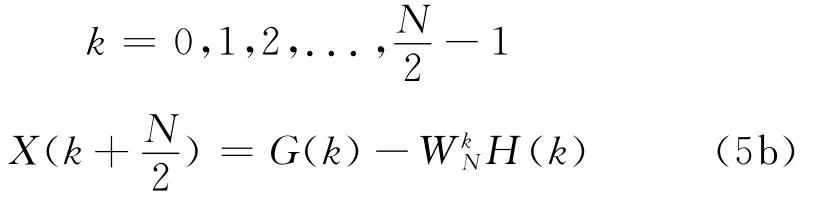
因此,一个抽样点数为N的信号序列x(n)的离散傅里叶变换,可以由两个N/2抽样点序列的离散傅里叶变换求出。依此类推,这种按时间抽取算法是将输入信号序列分成越来越小的子序列进行离散傅里叶变换计算,最后合成为N点的离散傅里叶变换。
本案例中选取当数组中N=128时,即进行快速傅里叶变换。由于采样频率为Fs=1 000 Hz,故本案例中某点n所对应的频率为:Fn=(n-1)Fs/N,Fn所能分辨到的频率为Fs/N=7.81 Hz。具体的原始信号的幅值与经过频谱变换之后的幅值的关系如下:假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值都是A的N/2倍。而第一个点就是直流分量,它的模值是直流分量的N倍。
以下举例说明时域信号与频域信号两者之间的关系。假设有一信号,含有3 V的直流分量;频率为50 Hz、相位为30°、幅度为1 V的交流信号;以及一频率为60 Hz、相位为60°、幅度为2.5 V的交流信号。其数学表达式如下:

以128 Hz的采样频率对这个信号进行采样,总共采样128点。Fn=(n-1)Fs/N,即每两个点之间的间距为1 Hz,第n个点的频率就是n-1。该信号有3个频率:0 Hz、50 Hz、60 Hz,应该分别在第1个点、第51个点、第61个点上出现峰值,其它各点应该接近0。其峰值依次为3×128=384、1×128/2=64、2.5×128/2=160。
电机振动的信号可以看成各个基波信号的叠加,经FFT变换之后,就可以看出各频率下信号的振动情况,从而了解电机的运行状况。
3 实验结果分析
为了验证测振仪的可靠性,选用淄博大元电机泵业有限公司生产的单相微型自吸泵在空载下进行振动检测,其额定功率为1.5 k W,额定转速为2 850 r/min。测量点为电机本体的水平方向,为了消除误差,进行了多次测量。图3为检测到的时域波形及频谱图。
从时域波形图上可以看出,检测到的振速始终在-0.6~+1.0(单位为:mm/s)之间,按照ISO2374和VDI2056的标准及机器设备的价值中对小型机器的振动标准的划分,此电机处于“较好”状态。分析频域波形,提取信号的频域特征,可为进一步分析电机的故障提供数据。
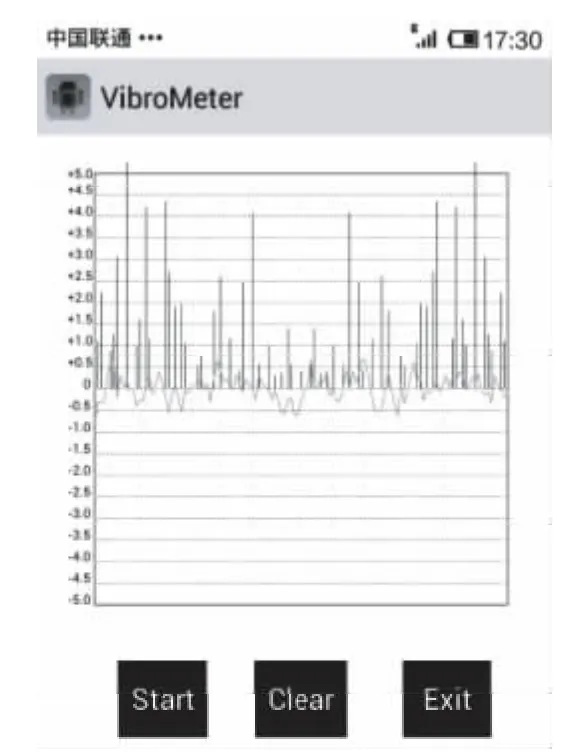
图3 检测到的时域波形及对应频谱图
4 结束语
本文介绍了一种基于Android平台下对智能手机中的加速度传感器在工业现场中对检测电机振动信号中的应用。通过开发,对Android平台下开发传感器的应用流程有了一定的了解。总的来说,将手机中内嵌的传感器应用于工业场合是完全可行的,相信在不久的将来智能手机及其内嵌传感器的工业应用会大放异彩。
[1] 马宏忠.电机状态检测与故障诊断[M].北京:机械工业出版社,2007.
[2] E.O.布里汉著,译.快速傅里叶变换[M].西安:科学技术出版社,1979.
[3] 何振亚.数字信号处理的理论与应用[M].北京:人民邮电出版社,1983.
[4] 程乾生.信号处理的数学原理[M].北京:北京大学出版社,2003.
[5] 王 济,胡 晓.MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社:知识产权出版社,2006.
[6] 高 凯,王俊社,仇 晶.Android智能手机软件开发教程[M].北京:国防工业出版社,2012.
[7] 佘志龙,陈昱勋,郑名杰,陈小风.Google Android SDK开发范例大全(第3版)[M].北京:人民邮电出版社,2011.
[8] 良葛格.Java JDK 5.0学习笔记[M].北京:清华大学出版社,2006.
